Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T22:00:02.659Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructive Packings by Linear Hypergraphs

Published online by Cambridge University Press:  12 September 2013

JILL DIZONA  and
BRENDAN NAGLE
JILL DIZONA
Affiliation:
Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA (e-mail: jdizona@mail.usf.edu, bnagle@usf.edu)
BRENDAN NAGLE
Affiliation:
Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA (e-mail: jdizona@mail.usf.edu, bnagle@usf.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For k-graphs F0 and H, an F0-packing of H is a family 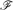$\mathscr{F}$ of pairwise edge-disjoint copies of F0 in H. Let νF0(H) denote the maximum size |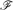$\mathscr{F}$| of an F0-packing of H. Already in the case of graphs, computing νF0(H) is NP-hard for most fixed F0 (Dor and Tarsi [6]).

In this paper, we consider the case when F0 is a fixed linear k-graph. We establish an algorithm which, for ζ > 0 and a given k-graph H, constructs in time polynomial in |V(H)| an F0-packing of H of size at least νF0(H) − ζ |V(H)|k. Our result extends one of Haxell and Rödl, who established the analogous algorithm for graphs.

Keywords

Primary 05C35Secondary 05C6505C85
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 6 , November 2013 , pp. 829 - 858
Copyright
Copyright © Cambridge University Press 2013 

References

[1]Alon, N. and Spencer, J. (1992) The Probabilistic Method, Wiley Interscience.Google Scholar
[2]Alon, N., Duke, R., Lefmann, H., Rödl, V. and Yuster, R. (1994) The algorithmic aspects of the Regularity Lemma. J. Algorithms 16 80–109.CrossRefGoogle Scholar
[3]Conlon, D., Hàn, H., Person, Y. and Schacht, M. (2012) Weak quasi-randomness for uniform hypergraphs. Random Struct. Alg. 40 1–38.CrossRefGoogle Scholar
[4]Czygrinow, A. Personal communication.Google Scholar
[5]Czygrinow, A. and Rödl, V. (2000) An algorithmic regularity lemma for hypergraphs. SIAM J. Comput. 30 1041–1066.CrossRefGoogle Scholar
[6]Dor, D. and Tarsi, M. (1992) Graph decomposition is NPC: A complete proof of Holyer's conjecture. In Proc. 20th ACM STOC, ACM Press, pp. 252–263.Google Scholar
[7]Frankl, P. and Rödl, V. (1992) The uniformity lemma for hypergraphs. Graphs Combin. 8 309–312.CrossRefGoogle Scholar
[8]Frankl, P. and Rödl, V. (2002) Extremal problems on set systems. Random Struct. Alg. 20 131–164.CrossRefGoogle Scholar
[9]Gowers, W. T. (2006) Quasirandomness, counting and regularity for 3-uniform hypergraphs. Combin. Probab. Comput. 15 143–184.CrossRefGoogle Scholar
[10]Gowers, W. T. (2007) Hypergraph regularity and the multidimensional Szemerédi theorem. Ann. of Math. (2) 166 897–946.CrossRefGoogle Scholar
[11]Grable, D. (1996) Nearly-perfect hypergraph packing is in NC. Inform. Process. Lett. 60 295–299.CrossRefGoogle Scholar
[12]Haxell, P. E. and Rödl, V. (2001) Integer and fractional packings in dense graphs. Combinatorica 21 13–38.CrossRefGoogle Scholar
[13]Haxell, P. E., Nagle, B. and Rödl, V. (2003) Integer and fractional packings in dense 3-uniform hypergraphs. Random Struct. Alg. 22 248–310.CrossRefGoogle Scholar
[14]Haxell, P. E., Nagle, B. and Rödl, V. (2005) An algorithmic version of the hypergraph regularity method [extended abstract]. In Proc. 46th Annual IEEE Symposium on Foundations of Computer Science: FOCS '05, pp. 439–448.CrossRefGoogle Scholar
[15]Haxell, P. E., Nagle, B. and Rödl, V. (2008) An algorithmic version of the hypergraph regularity method. SIAM J. Comput. 37 1728–1776.CrossRefGoogle Scholar
[16]Janson, S., Luczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.CrossRefGoogle Scholar
[17]Kohayakawa, Y., Nagle, B., Rödl, V. and Schacht, M. (2010) Weak hypergraph regularity and linear hypergraphs. J. Combin. Theory Ser. B 100 151–160.CrossRefGoogle Scholar
[18]Kohayakawa, Y., Rödl, V. and Thoma, L. (2003) An optimal algorithm for checking regularity. SIAM J. Comput. 32 1210–1235.CrossRefGoogle Scholar
[19]Nagle, B., Poerschke, A., Rödl, V. and Schacht, M. (2009) Hypergraph regularity and quasirandomness. In Proc. 20th Annual ACM–SIAM Symposium on Discrete Algorithms: SODA '09 (Mathieu, C., ed.), ACM Press, pp. 227–245.Google Scholar
[20]Rödl, V. and Skokan, J. (2004) Regularity lemma for uniform hypergraphs. Random Struct. Alg. 25 1–42.CrossRefGoogle Scholar
[21]Rödl, V., Schacht, M., Siggers, M. H. and Tokushige, N. (2007) Integer and fractional packings of hypergraphs. J. Combin. Theory Ser. B 97 245–268CrossRefGoogle Scholar
[22]Skokan, J. and Thoma, L. (2004) Bipartite subgraphs and quasi-randomness. Graphs Combin. 20 255–262.CrossRefGoogle Scholar
[23]Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arithmetica 27 199–245.CrossRefGoogle Scholar
[24]Szemerédi, E. (1978) Regular partitions of graphs. In Problèmes en Combinatoires et Théorie des Graphes: Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976, CNRS, pp. 399–401.Google Scholar
[25]Williams, V. V. (2012) Multiplying matrices faster than Coppersmith–Winograd. In Proc. 44th Symposium on Theory of Computing: STOC '12, ACM Press, pp. 887–898.CrossRefGoogle Scholar
[26]Yuster, R. (2005) Integer and fractional packings of families of graphs. Random Struct. Alg 26 110–118.CrossRefGoogle Scholar