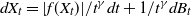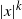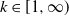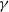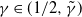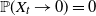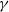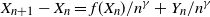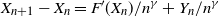1. Introduction
Let ![]() $F\,:\,\mathbb{R}^d \rightarrow \mathbb{R}^d, d \geq 1$, be a vector field. For much of what follows F arises as the gradient of a potential function V, namely
$F\,:\,\mathbb{R}^d \rightarrow \mathbb{R}^d, d \geq 1$, be a vector field. For much of what follows F arises as the gradient of a potential function V, namely ![]() $V\,:\,\mathbb{R}^d \rightarrow \mathbb{R}$, and
$V\,:\,\mathbb{R}^d \rightarrow \mathbb{R}$, and ![]() $F=-\nabla V$. Now, we define a system driven by
$F=-\nabla V$. Now, we define a system driven by
To elaborate on the parameters, let ![]() $\mathcal{F}_n$ be a filtration; then
$\mathcal{F}_n$ be a filtration; then ![]() $a_n,\xi_n$ are adapted, and the
$a_n,\xi_n$ are adapted, and the ![]() $\xi_n$ constitute martingale differences, i.e.
$\xi_n$ constitute martingale differences, i.e. ![]() $\mathbb{E}(\xi_{n+1}|\mathcal{F}_n) = 0$. For the purposes of this introduction we will simplify and assume, without any great loss of abstraction, that
$\mathbb{E}(\xi_{n+1}|\mathcal{F}_n) = 0$. For the purposes of this introduction we will simplify and assume, without any great loss of abstraction, that ![]() $a_n$ is deterministic and either is a constant number or is converging to zero comparably to
$a_n$ is deterministic and either is a constant number or is converging to zero comparably to ![]() $n^{-\gamma}$ (i.e. it is
$n^{-\gamma}$ (i.e. it is ![]() $\Theta\left(n^{-\gamma}\right)$), where
$\Theta\left(n^{-\gamma}\right)$), where ![]() $\gamma \in (1/2,1]$. Also, some additional assumptions on the noise are usually required: one is a boundedness constraint, that is, we assume the existence of a constant M such that
$\gamma \in (1/2,1]$. Also, some additional assumptions on the noise are usually required: one is a boundedness constraint, that is, we assume the existence of a constant M such that ![]() $|\xi_n|\leq M$ almost surely (a.s.); and secondly we want
$|\xi_n|\leq M$ almost surely (a.s.); and secondly we want ![]() $\xi_n$ to be quasi-isotropic (see [Reference Daneshmand, Kohler, Lucchi and HofmannDKLH18]), i.e.,
$\xi_n$ to be quasi-isotropic (see [Reference Daneshmand, Kohler, Lucchi and HofmannDKLH18]), i.e., ![]() $\mathbb{P}( (\theta \cdot \xi_n)^{+}>\delta )>\delta$ for any unit direction
$\mathbb{P}( (\theta \cdot \xi_n)^{+}>\delta )>\delta$ for any unit direction ![]() $\theta \in \mathbb{R}^d$. This condition makes sure that the process gets jiggled in every direction. This versatile system is well studied, and it arises naturally in many different areas. In machine learning and statistics, (1) can be a powerful tool for quick optimization and statistical inference (see [Reference AgarwalAAZB+17], [Reference Li, Liu, Kyrillidis and CaramanisLLKC18], [Reference Chen, Lee, Tong and ZhangCdlTTZ16]), among other uses. Furthermore, many urn models are represented by (1). These processes play a central role in probability theory due to their wide applicability in physics, biology, and social sciences; for a comprehensive exposition on the subject see [Reference PemantlePem07].
$\theta \in \mathbb{R}^d$. This condition makes sure that the process gets jiggled in every direction. This versatile system is well studied, and it arises naturally in many different areas. In machine learning and statistics, (1) can be a powerful tool for quick optimization and statistical inference (see [Reference AgarwalAAZB+17], [Reference Li, Liu, Kyrillidis and CaramanisLLKC18], [Reference Chen, Lee, Tong and ZhangCdlTTZ16]), among other uses. Furthermore, many urn models are represented by (1). These processes play a central role in probability theory due to their wide applicability in physics, biology, and social sciences; for a comprehensive exposition on the subject see [Reference PemantlePem07].
In machine learning, processes satisfying (1) appear in stochastic gradient descent (SGD). First, to provide context, let us briefly introduce the gradient descent method (GD) and then see why SGD arises naturally from it. The GD is an optimization technique which finds local minima for a potential function V via the iteration
where in many applications we take ![]() $\eta_n$ to be positive and constant. Notice that (2) is a specialization of (1), with
$\eta_n$ to be positive and constant. Notice that (2) is a specialization of (1), with ![]() $F=-\nabla V$,
$F=-\nabla V$, ![]() $\xi_{n+1}\equiv 0$, and
$\xi_{n+1}\equiv 0$, and ![]() $a_n=\eta_n$. The above method when applied to non-convex functions has the shortcoming that it may get stuck near saddle points (i.e. points where the gradient vanishes, that are neither local minima nor local maxima), or may locate local minima instead of global ones. The former issue can be resolved by adding noise into the system, which, consequently, helps in pushing the particle downhill and eventually escaping saddle points (see [Reference PemantlePem90] and [Reference Kushner and YinKY03, Section 5.8]). For the latter, in general, avoiding local minima is a difficult problem ([Reference Gelfand and MitterGM91] and [Reference Raginsky, Rakhlin and TelgarskyRRT17]); however, fortunately, in many instances finding local minima is satisfactory. Recently there have been several problems of interest where this is indeed the case, either because all local minima are global minima ([Reference Ge, Huang, Jin and YuanGHJY15] and [Reference Sun, Qu and WrightSQW17]), or, in other cases, because local minima provide equally good results as global minima [Reference ChoromanskaCHM15]. Furthermore, in certain applications saddle points lead to highly suboptimal results ([Reference Jain, Jin, Kakade and NetrapalliJJKN15] and [Reference Sun and LuoSL16]), which highlights the importance of escaping saddle points.
$a_n=\eta_n$. The above method when applied to non-convex functions has the shortcoming that it may get stuck near saddle points (i.e. points where the gradient vanishes, that are neither local minima nor local maxima), or may locate local minima instead of global ones. The former issue can be resolved by adding noise into the system, which, consequently, helps in pushing the particle downhill and eventually escaping saddle points (see [Reference PemantlePem90] and [Reference Kushner and YinKY03, Section 5.8]). For the latter, in general, avoiding local minima is a difficult problem ([Reference Gelfand and MitterGM91] and [Reference Raginsky, Rakhlin and TelgarskyRRT17]); however, fortunately, in many instances finding local minima is satisfactory. Recently there have been several problems of interest where this is indeed the case, either because all local minima are global minima ([Reference Ge, Huang, Jin and YuanGHJY15] and [Reference Sun, Qu and WrightSQW17]), or, in other cases, because local minima provide equally good results as global minima [Reference ChoromanskaCHM15]. Furthermore, in certain applications saddle points lead to highly suboptimal results ([Reference Jain, Jin, Kakade and NetrapalliJJKN15] and [Reference Sun and LuoSL16]), which highlights the importance of escaping saddle points.
As described in the previous paragraph, escaping saddle points when performing SGD is an important problem. The saddle problem is well understood when nondegeneracy conditions are imposed. Results showing that asymptotically SGD will escape saddle points date back to works of Pemantle [Reference PemantlePem91] and, more recently, [Reference Lee, Simchowitz, Jordan and RechtLSJR16], where the authors prove that random initialization guarantees almost sure convergence to minimizers. The establishment of asymptotic convergence subsequently led to results on how this can be done efficiently [Reference Lee, Simchowitz, Jordan and RechtLSJR16].
Processes satisfying (1), when ![]() $a_n$ goes to zero, are known as stochastic approximations, after [Reference Robbins and MonroRM51]. These processes have been extensively studied since then [Reference Kushner and YinKY03]. An important feature is that the step size
$a_n$ goes to zero, are known as stochastic approximations, after [Reference Robbins and MonroRM51]. These processes have been extensively studied since then [Reference Kushner and YinKY03]. An important feature is that the step size ![]() $a_n$ satisfies
$a_n$ satisfies
This property balances the effects of the noise in the system, so that there is an implicit averaging that, eventually, eliminates the effects of the noise. The previously described system hence behaves similarly to the mean flow: the ordinary differential equation whose right-hand side corresponds to the expectation of the driving term (![]() $F(X_t)$). This heuristic can help us identify the support S of the limiting process
$F(X_t)$). This heuristic can help us identify the support S of the limiting process ![]() $X_\infty \,{:}\,{\raise-1.5pt{=}}\, \lim_{n \rightarrow \infty} X_n$ in terms of the topological properties of the dynamical system
$X_\infty \,{:}\,{\raise-1.5pt{=}}\, \lim_{n \rightarrow \infty} X_n$ in terms of the topological properties of the dynamical system ![]() $\frac{\text{d }\!X_t^{\vphantom{a}} }{ \text{d }\!\! t}=F(X_t) $ (see [Reference Kushner and YinKY03, Chapter 5]). More specifically, in most instances, one can argue that attractors are in S, whereas repellers or ‘strict’ saddle points are not (see [Reference Kushner and YinKY03, Section 5.8]). However, there has not been a systematic approach to finding when a degenerate saddle point, i.e. a point that is neither an attractor nor a repeller, belongs in S.
$\frac{\text{d }\!X_t^{\vphantom{a}} }{ \text{d }\!\! t}=F(X_t) $ (see [Reference Kushner and YinKY03, Chapter 5]). More specifically, in most instances, one can argue that attractors are in S, whereas repellers or ‘strict’ saddle points are not (see [Reference Kushner and YinKY03, Section 5.8]). However, there has not been a systematic approach to finding when a degenerate saddle point, i.e. a point that is neither an attractor nor a repeller, belongs in S.
Stochastic approximations arise naturally in many different contexts. Some early results were published by [Reference RuppertRup88] and [Reference Polyak and JuditskyPJ92]. There, the authors dealt with averaged stochastic gradient descent (ASGD) arising from a strongly convex potential V with step size ![]() $n^{-\gamma}, \gamma \in (1/2,1]$. In their work they proved that one can build, with proper scaling, consistent estimators
$n^{-\gamma}, \gamma \in (1/2,1]$. In their work they proved that one can build, with proper scaling, consistent estimators ![]() $\tilde{x}_n$ (for the
$\tilde{x}_n$ (for the ![]() $\arg \min(V)$) whose limiting distribution is Gaussian. In learning problems, a modified version of ASGD [Reference Rakhlin, Shamir and SridharanRSS12] provides convergence rates to global minima of order
$\arg \min(V)$) whose limiting distribution is Gaussian. In learning problems, a modified version of ASGD [Reference Rakhlin, Shamir and SridharanRSS12] provides convergence rates to global minima of order ![]() $n^{-1}$. Additionally, many classical urn processes can be described via (1), where
$n^{-1}$. Additionally, many classical urn processes can be described via (1), where ![]() $a_{n}$ is of the order of
$a_{n}$ is of the order of ![]() $n^{-1}$. Certain efforts are being made towards understanding the support of the limiting process
$n^{-1}$. Certain efforts are being made towards understanding the support of the limiting process ![]() $X_{\infty}$. In specific instances, the underlying problem boils down to understanding an SGD problem: to characterize the support of
$X_{\infty}$. In specific instances, the underlying problem boils down to understanding an SGD problem: to characterize the support of ![]() $X_\infty$ in terms of the class of critical points of the corresponding potential V. For a comprehensive exposition on urn processes see [Reference PemantlePem07].
$X_\infty$ in terms of the class of critical points of the corresponding potential V. For a comprehensive exposition on urn processes see [Reference PemantlePem07].
From the previous discussion, some fundamental questions of interest regarding (1) are the following:
1. Does
 $X_n$ converge?
$X_n$ converge?-
2. When does
 $X_n$ converge to (local) minima, consequently avoiding saddle points?
$X_n$ converge to (local) minima, consequently avoiding saddle points? -
3. When does
 $X_n$ converge to global minima?
$X_n$ converge to global minima? -
4. How fast does
 $X_n$ converge to local minima?
$X_n$ converge to local minima?
When F arises from a potential function V, the first question is for the most part settled: the limit of the process converges, and it is supported on a subset of the set of critical points of V (see [Reference Kushner and YinKY03, Chapter 5]).
Here, our primary focus will be understanding the second question in a one-dimensional setting. More specifically, we will work with processes that solve
To put this in context, the antiderivative of ![]() $-f$ would correspond to the potential function
$-f$ would correspond to the potential function ![]() $-V$. Therefore, if a point p has a neighborhood
$-V$. Therefore, if a point p has a neighborhood ![]() $\mathcal{N}$ such that f is positive except for
$\mathcal{N}$ such that f is positive except for ![]() $f(p)=0$, then the point p would be a saddle point.
$f(p)=0$, then the point p would be a saddle point.
Problem 1.1. Let ![]() $(X_n)_{\geq 1}$ solve (3). Suppose that p is a saddle point. Find the threshold value, denoted
$(X_n)_{\geq 1}$ solve (3). Suppose that p is a saddle point. Find the threshold value, denoted ![]() $\tilde{\gamma}$, for
$\tilde{\gamma}$, for ![]() $\gamma$, should it exist, such that the following hold:
$\gamma$, should it exist, such that the following hold:
1. When
 $\gamma \in (1/2, \tilde{\gamma})$,
$\gamma \in (1/2, \tilde{\gamma})$,  $\mathbb{P}(X_n\rightarrow p) = 0$.
$\mathbb{P}(X_n\rightarrow p) = 0$.2. When
 $\gamma \in (\tilde{\gamma},1]$,
$\gamma \in (\tilde{\gamma},1]$,  $\mathbb{P}(X_n\rightarrow p)>0$.
$\mathbb{P}(X_n\rightarrow p)>0$.
Part 1 of Problem 1.1 guarantees that the SGD avoids saddle points, and hence converges to local minima. Choosing ![]() $\gamma$ appropriately in the first regime (i.e.
$\gamma$ appropriately in the first regime (i.e. ![]() $\gamma\in (1/2, \tilde{\gamma})$) enables us to optimize the performance of the SGD. In practice, choosing a small step size can slow the rate of convergence; however, a bigger step size may lead the process to bounce around (see [Reference Brennan and RogersBR95] and [Reference Suri and LeungSL87]). In [Reference Even-Dar and MansourEDM01] the authors study the rate of convergence for polynomial step sizes in the context of Q-learning for Markov decision processes, and they experimentally demonstrate that for
$\gamma\in (1/2, \tilde{\gamma})$) enables us to optimize the performance of the SGD. In practice, choosing a small step size can slow the rate of convergence; however, a bigger step size may lead the process to bounce around (see [Reference Brennan and RogersBR95] and [Reference Suri and LeungSL87]). In [Reference Even-Dar and MansourEDM01] the authors study the rate of convergence for polynomial step sizes in the context of Q-learning for Markov decision processes, and they experimentally demonstrate that for ![]() $\gamma$ approximately
$\gamma$ approximately ![]() $\tfrac{17}{20}$ the rate of convergence is optimal.
$\tfrac{17}{20}$ the rate of convergence is optimal.
In the literature there are many results of this type. However, as already mentioned, the vast majority of them require the saddle points to satisfy certain nondegeneracy conditions. In fact, nondegenerate saddle points will never be in the support of ![]() $X_\infty$. Interestingly enough, the previous conclusion is not always valid for degenerate ones; see [Reference PemantlePem91], in which the support of
$X_\infty$. Interestingly enough, the previous conclusion is not always valid for degenerate ones; see [Reference PemantlePem91], in which the support of ![]() $X_\infty$ for a generalized urn model [Reference Hill, D. and SudderthHLS80] fitting (3) for
$X_\infty$ for a generalized urn model [Reference Hill, D. and SudderthHLS80] fitting (3) for ![]() $\gamma=1$ is characterized in terms of a ‘general’ function f. However, we show that for any V, under some mild conditions, we can find
$\gamma=1$ is characterized in terms of a ‘general’ function f. However, we show that for any V, under some mild conditions, we can find ![]() $\gamma$ such that saddle points do not belong to S (see Theorems 1.2 and 1.4). Hence, we demonstrate that implementing SGD, by adding enough noise, gives the desired asymptotic behavior even in the degenerate case.
$\gamma$ such that saddle points do not belong to S (see Theorems 1.2 and 1.4). Hence, we demonstrate that implementing SGD, by adding enough noise, gives the desired asymptotic behavior even in the degenerate case.
It is the hope of the author that this work is a step towards understanding a broader class of non-convex problems. One prospective application would be analyzing complex systems that can be studied by finding a corresponding simpler one-dimensional system. Although non-convex optimization problems are, generally, NP-hard (for a discussion in the context of escaping saddle points see [Reference Anandkumar and GeAG16]), it would be possible to extend the results of this paper to certain classes of problems in higher dimensions, as we are focusing on the asymptotic behavior of the system. Potentially, such an extension can be achieved by reducing the multidimensional problem to a suitable one-dimensional problem and then applying the results of this paper. For an example where the analysis of the asymptotic behavior of a system of stochastic approximations relies on reducing the problem to a one-dimensional problem, see [Reference PemantlePem90]. Also we are trying to establish that if we understand the underlying dynamical system sufficiently, then by adding enough noise, we can guarantee that the process will wander until it is captured by a downhill path, and thus it will eventually escape the unstable neighborhood. Finally, this paper, and even more so a multidimensional extension of it, can serve as a theoretical guarantee of convergence, much in the spirit of the works of [Reference Lee, Simchowitz, Jordan and RechtLSJR16] and [Reference PemantlePem90], which were succeeded by efficient algorithms [Reference JinJGN+17].
To extend results to the multidimensional setting using this paper, one would need to find a suitable corresponding one-dimensional system. One potential path to accomplish this is to use a Łojasiewicz-type inequality; for a reference see [Spr, Theorem 2] and [Reference SonSon12, Lemma 3.2, p. 315]. Before we state the inequality we will need a definition.
Definition 1.1. Suppose that ![]() $V\,:\,\mathbb{R}^n \to \mathbb{R}$. The zero set of V is denoted by
$V\,:\,\mathbb{R}^n \to \mathbb{R}$. The zero set of V is denoted by ![]() $Z_V = \{x\in \mathbb{R}^n : V(x)=0 \}$.
$Z_V = \{x\in \mathbb{R}^n : V(x)=0 \}$.
Theorem 1.1. Let V be defined as before. Let ![]() $Z_V$ denote the zero set of V. Then there is an open set
$Z_V$ denote the zero set of V. Then there is an open set ![]() $0\in \mathcal{O}$ such that there is a positive constant
$0\in \mathcal{O}$ such that there is a positive constant ![]() $k\in(1,2)$ such that the following holds:
$k\in(1,2)$ such that the following holds:
Now suppose that ![]() $X_n$ satisfies (1), where
$X_n$ satisfies (1), where ![]() $F(\cdot)=-V$ where
$F(\cdot)=-V$ where ![]() $a_n = \frac{1}{n^\gamma}$. Furthermore, assume
$a_n = \frac{1}{n^\gamma}$. Furthermore, assume ![]() $V\,:\,\mathbb{R}^d\rightarrow \mathbb{R}$ is an analytic function such that
$V\,:\,\mathbb{R}^d\rightarrow \mathbb{R}$ is an analytic function such that ![]() $V(0)=\nabla V(0)=0$. Hereby, we assume that 0 is a saddle point and that it is also an isolated critical point.
$V(0)=\nabla V(0)=0$. Hereby, we assume that 0 is a saddle point and that it is also an isolated critical point.
To study whether ![]() $X_n\to 0$, our candidate line of attack consists of three distinct steps.
$X_n\to 0$, our candidate line of attack consists of three distinct steps.
• We start by studying the process
 $(V(X_n))_{n\geq 1}$. Then Theorem 1.1 should give an upper bound on
$(V(X_n))_{n\geq 1}$. Then Theorem 1.1 should give an upper bound on  $|V(X_n)|$.
$|V(X_n)|$.• Then the process
 $X_n$ may wander into the realm where
$X_n$ may wander into the realm where  $V(X_n)<0$ with probability bounded from below.
$V(X_n)<0$ with probability bounded from below.• Lastly, we show that when
 $V(X_n) <0$, the process may stay negative with probability bounded from below; hence we conclude that
$V(X_n) <0$, the process may stay negative with probability bounded from below; hence we conclude that  $\mathbb{P}(X_n\rightarrow 0) =0$.
$\mathbb{P}(X_n\rightarrow 0) =0$.
For the second part of the strategy we notice that the path from ![]() $X_n$ to
$X_n$ to ![]() $z\in Z_V$ along the flow
$z\in Z_V$ along the flow ![]() $x'_t= -\nabla V(x_t)$ has length
$x'_t= -\nabla V(x_t)$ has length ![]() $V(X_n)$. So we should expect that as long as
$V(X_n)$. So we should expect that as long as ![]() $V(X_n)$ and the remaining noise in the recursion (1) are comparable, then
$V(X_n)$ and the remaining noise in the recursion (1) are comparable, then ![]() $X_n$ may wander into the realm where
$X_n$ may wander into the realm where ![]() $V(X_n)<0$.
$V(X_n)<0$.
To expand on the third step we need the following definition.
Definition 1.2. Suppose that ![]() $V\,:\,\mathbb{R}^n\to \mathbb{R}$ and let
$V\,:\,\mathbb{R}^n\to \mathbb{R}$ and let ![]() $x \in \mathbb{R}^n$ such that
$x \in \mathbb{R}^n$ such that ![]() $V(x)<0$. Denote by
$V(x)<0$. Denote by ![]() $\mathcal{O}_x$ the connected component of
$\mathcal{O}_x$ the connected component of ![]() $ \{ x \in \mathbb{R}^n\,:\,V(x) \leq 0 \}$ such that
$ \{ x \in \mathbb{R}^n\,:\,V(x) \leq 0 \}$ such that ![]() $x \in \mathcal{O}_x$.
$x \in \mathcal{O}_x$.
For the last step of the strategy we ought to understand the geometry of the conical region ![]() $\mathcal{O}_{X_n}\cap Z_V$. For instance, the surface
$\mathcal{O}_{X_n}\cap Z_V$. For instance, the surface ![]() $\mathcal{O}_{X_n}\cap Z_V$ may be very steep, so that under the slightest perturbation the iterates
$\mathcal{O}_{X_n}\cap Z_V$ may be very steep, so that under the slightest perturbation the iterates ![]() $X_n$ may return to the realm
$X_n$ may return to the realm ![]() $V(X_n)>0$. It is important to note that in certain instances, depending on the surface
$V(X_n)>0$. It is important to note that in certain instances, depending on the surface ![]() $\mathcal{O}_{X_n}\cap Z_V$, there could be a degenerate saddle point where the iterates could get stuck. However, if we assume, for example, that V is a homogeneous polynomial, then the angular size of this surface near the origin is not changing over time, and so we should expect a probability bounded from below that the process crosses into the region with
$\mathcal{O}_{X_n}\cap Z_V$, there could be a degenerate saddle point where the iterates could get stuck. However, if we assume, for example, that V is a homogeneous polynomial, then the angular size of this surface near the origin is not changing over time, and so we should expect a probability bounded from below that the process crosses into the region with ![]() $V(X_n)<-\delta t^{\frac{1-\gamma}{1-k }}$, where k is given by Theorem 1.1. To gain intuition on the previous bound one can look at the proof of Proposition 6.1.
$V(X_n)<-\delta t^{\frac{1-\gamma}{1-k }}$, where k is given by Theorem 1.1. To gain intuition on the previous bound one can look at the proof of Proposition 6.1.
1.1. Results for the continuous model
We proceed by transitioning to a continuous model. For that purpose we need a potential, a step size, and a noise. However, it is natural to consider, without the need to contemplate, a process defined by
We assume that ![]() $f(0)=0$ and that f is otherwise positive in a neighborhood
$f(0)=0$ and that f is otherwise positive in a neighborhood ![]() $\mathcal{N}$ of zero. What we wish to investigate is whether
$\mathcal{N}$ of zero. What we wish to investigate is whether ![]() $L_t$ will not converge to 0 with probability 1, or will converge there with some positive probability. The answer to these questions depends only on the local behavior of f on
$L_t$ will not converge to 0 with probability 1, or will converge there with some positive probability. The answer to these questions depends only on the local behavior of f on ![]() $\mathcal{N}$.
$\mathcal{N}$.
The main non-convergence result is the following.
Theorem 1.2. Suppose that ![]() $\mathcal{N}$ is a neighborhood of zero. Let
$\mathcal{N}$ is a neighborhood of zero. Let ![]() $(L_t)_{t\geq 1}$ be a solution of (4), where f(x) is Lipschitz. We distinguish two cases depending on f and the parameters of the system:
$(L_t)_{t\geq 1}$ be a solution of (4), where f(x) is Lipschitz. We distinguish two cases depending on f and the parameters of the system:
1.
 $k|x| \leq f(x) $,
$k|x| \leq f(x) $,  $k> \frac{1}{2}$, and
$k> \frac{1}{2}$, and  $ \gamma =1$ for all
$ \gamma =1$ for all  $x\in \mathcal{N}$.
$x\in \mathcal{N}$.2.
 $ |x|^k \leq f(x)\,$,
$ |x|^k \leq f(x)\,$,  $\frac{1}{2}+\frac{1}{2k} \geq \gamma$, and
$\frac{1}{2}+\frac{1}{2k} \geq \gamma$, and  $k>1$ for all
$k>1$ for all  $x\in \mathcal{N}$.
$x\in \mathcal{N}$.
If either 1 or 2 holds, then ![]() $\mathbb{P}(L_t\rightarrow 0)=0$.
$\mathbb{P}(L_t\rightarrow 0)=0$.
In the first part of the theorem, the result holds even in the case ![]() $k=\frac{1}{2}$; however, the proof is omitted to avoid repetition. In Part 1, we have only considered
$k=\frac{1}{2}$; however, the proof is omitted to avoid repetition. In Part 1, we have only considered ![]() $\gamma=1$ since that is the only critical case; that is, for
$\gamma=1$ since that is the only critical case; that is, for ![]() $\gamma<1$ the effects of the noise would be overwhelming and for all k we would obtain
$\gamma<1$ the effects of the noise would be overwhelming and for all k we would obtain ![]() $\mathbb{P}(L_t\rightarrow 0)=0$.
$\mathbb{P}(L_t\rightarrow 0)=0$.
We now state the main convergence theorem.
Theorem 1.3. Suppose that ![]() $\mathcal{N}$ is a neighborhood of zero. Let
$\mathcal{N}$ is a neighborhood of zero. Let ![]() $(L_t)_{t\geq 1}$ be a solution of (4). We distinguish two cases depending on f and the parameters of the system:
$(L_t)_{t\geq 1}$ be a solution of (4). We distinguish two cases depending on f and the parameters of the system:
1.
 $k_1|x|\leq f(x)\leq k_2|x|$,
$k_1|x|\leq f(x)\leq k_2|x|$,  $0<k_i<1/2$, and
$0<k_i<1/2$, and  $\gamma=1$ for all
$\gamma=1$ for all  $x\in \mathcal{N}\cap(-\infty,0]$.
$x\in \mathcal{N}\cap(-\infty,0]$.2.
 $0<c|x|^k \leq f(x)\leq|x|^k$,
$0<c|x|^k \leq f(x)\leq|x|^k$,  $\frac{1}{2}+\frac{1}{2k} >\gamma$, and
$\frac{1}{2}+\frac{1}{2k} >\gamma$, and  $k>1$ for all
$k>1$ for all  $x\in \mathcal{N}\cap(-\infty,0]$.
$x\in \mathcal{N}\cap(-\infty,0]$.
If either 1 or 2 holds, then ![]() $\mathbb{P}(L_t\rightarrow 0)>0$.
$\mathbb{P}(L_t\rightarrow 0)>0$.
This is proved by first establishing the previous results for monomials, i.e. ![]() $f(x)=|x|^k$ or
$f(x)=|x|^k$ or ![]() $f(x)=k|x|$, which is done in Sections 3 and 4. We prove the stated theorems in Section 5, by utilizing the comparison results found in Section 2.
$f(x)=k|x|$, which is done in Sections 3 and 4. We prove the stated theorems in Section 5, by utilizing the comparison results found in Section 2.
In Section 3 we deal with the linear case, i.e. ![]() $f(x)=k|x|$. There, the stochastic differential equation (SDE) can be explicitly solved, which simplifies matters to a great extent. Firstly, in Subsection 3.2, we prove that when
$f(x)=k|x|$. There, the stochastic differential equation (SDE) can be explicitly solved, which simplifies matters to a great extent. Firstly, in Subsection 3.2, we prove that when ![]() $k>1/2$, the corresponding process a.s. will not converge to 0, which is accomplished by proving that it will converge to infinity a.s. Secondly, in Subsection 3.3, we show that when
$k>1/2$, the corresponding process a.s. will not converge to 0, which is accomplished by proving that it will converge to infinity a.s. Secondly, in Subsection 3.3, we show that when ![]() $k<1/2$, the process will converge to 0 with some positive probability.
$k<1/2$, the process will converge to 0 with some positive probability.
In Section 4 we move on to the higher-order monomials, i.e. ![]() $f(x)=|x|^k$. Here we show that the process will behave as the ‘mean flow’ process h(t) infinitely often; this is accomplished by studying the process
$f(x)=|x|^k$. Here we show that the process will behave as the ‘mean flow’ process h(t) infinitely often; this is accomplished by studying the process ![]() $L_t/h(t)$. In Subsection 4.2, the main theorem is that when
$L_t/h(t)$. In Subsection 4.2, the main theorem is that when ![]() $\frac{1}{2}+\frac{1}{2k}\geq\gamma$,
$\frac{1}{2}+\frac{1}{2k}\geq\gamma$, ![]() $L_t\rightarrow \infty$ a.s. In Subsection 4.3, we show that when
$L_t\rightarrow \infty$ a.s. In Subsection 4.3, we show that when ![]() $\frac{1}{2}+\frac{1}{2k}<\gamma$, the process may converge to 0 with positive probability.
$\frac{1}{2}+\frac{1}{2k}<\gamma$, the process may converge to 0 with positive probability.
Qualitatively, the previous constraints on the parameters are in accordance with our intuition. To be more specific, when k increases, f becomes steeper, which should indicate it is easier for the process to escape. When ![]() $\gamma$ decreases the remaining variance increases; hence we should expect that the process visits the unstable trajectory with greater ease, due to higher fluctuations.
$\gamma$ decreases the remaining variance increases; hence we should expect that the process visits the unstable trajectory with greater ease, due to higher fluctuations.
1.2. Results for the discrete model
The asymptotic behavior of the discrete processes is the expected one, depending on the parameters of the problem. Here, we study processes satisfying
or
where ![]() $Y_n$ are a.s. bounded (i.e. there is a constant M such that
$Y_n$ are a.s. bounded (i.e. there is a constant M such that ![]() $|Y_n|<M$ a.s.),
$|Y_n|<M$ a.s.), ![]() $\mathbb{E}(Y_{n+1}|\mathcal{F}_n)=0$, and
$\mathbb{E}(Y_{n+1}|\mathcal{F}_n)=0$, and ![]() $ \mathbb{E}(Y_{n+1}^2|\mathcal{F}_n )\geq l>0 $. The main non-convergence theorem is the following.
$ \mathbb{E}(Y_{n+1}^2|\mathcal{F}_n )\geq l>0 $. The main non-convergence theorem is the following.
Theorem 1.4. Suppose that ![]() $\mathcal{N}$ is a neighborhood of zero. Let
$\mathcal{N}$ is a neighborhood of zero. Let ![]() $(X_n)_{n\geq 1}$ solve (5). If
$(X_n)_{n\geq 1}$ solve (5). If ![]() $|x|^k \leq f(x)$,
$|x|^k \leq f(x)$, ![]() $\frac{1}{2}+\frac{1}{2k} > \gamma$, and
$\frac{1}{2}+\frac{1}{2k} > \gamma$, and ![]() $k>1$ for all
$k>1$ for all ![]() $x\in \mathcal{N}$, then
$x\in \mathcal{N}$, then ![]() $\mathbb{P}(X_n\rightarrow 0)=0$. For the convergence result the nondegeneracy condition
$\mathbb{P}(X_n\rightarrow 0)=0$. For the convergence result the nondegeneracy condition ![]() $\mathbb{E}(Y_{n+1}^2|\mathcal{F}_n)\geq l$ is replaced with the assumption stated in Part 1 of Theorem 1.5.
$\mathbb{E}(Y_{n+1}^2|\mathcal{F}_n)\geq l$ is replaced with the assumption stated in Part 1 of Theorem 1.5.
Theorem 1.5. Let ![]() $\mathcal{N}=(-3\epsilon,3\epsilon)$ be a neighborhood of zero. Suppose
$\mathcal{N}=(-3\epsilon,3\epsilon)$ be a neighborhood of zero. Suppose ![]() $(X_n)_{n\geq 1}$ solve (6). Assume the following:
$(X_n)_{n\geq 1}$ solve (6). Assume the following:
1. There exist
 $-\epsilon_2>-3\epsilon$ and
$-\epsilon_2>-3\epsilon$ and  $-\epsilon_1<-\epsilon $ such that for all
$-\epsilon_1<-\epsilon $ such that for all  $M>0$, there exists
$M>0$, there exists  $n>M$ such that
$n>M$ such that  $\mathbb{P}(X_n \in (-\epsilon_2,-\epsilon_1 ) ) >0$.
$\mathbb{P}(X_n \in (-\epsilon_2,-\epsilon_1 ) ) >0$.2.
 $ 0<f(x)\leq |x|^k$,
$ 0<f(x)\leq |x|^k$,  $\frac{1}{2}+\frac{1}{2k}< \gamma$, and
$\frac{1}{2}+\frac{1}{2k}< \gamma$, and  $k>1$ for all
$k>1$ for all  $x\in \mathcal{N}$.
$x\in \mathcal{N}$.
Then ![]() $\mathbb{P}(X_n\rightarrow 0 )>0$.
$\mathbb{P}(X_n\rightarrow 0 )>0$.
The assumption imposed on ![]() $X_n$, Part 1 of Theorem 1.5, says that the process should be able visit a neighborhood of the origin for large enough n. If this constraint is not imposed on the process, the previous result need not hold. For instance, the drift could dominate the noise, and consequently the process might never reach a neighborhood of the origin with probability 1. There are processes that naturally satisfy this property; an example is the urn process defined in Section 1 (see [Reference PemantlePem91]).
$X_n$, Part 1 of Theorem 1.5, says that the process should be able visit a neighborhood of the origin for large enough n. If this constraint is not imposed on the process, the previous result need not hold. For instance, the drift could dominate the noise, and consequently the process might never reach a neighborhood of the origin with probability 1. There are processes that naturally satisfy this property; an example is the urn process defined in Section 1 (see [Reference PemantlePem91]).
Example 1.1. Suppose that ![]() $X_n$ satisfies
$X_n$ satisfies
where the ![]() $U_n$ are independent and identically distributed variables, uniformly distributed on
$U_n$ are independent and identically distributed variables, uniformly distributed on ![]() $ (-2,2)$. As the
$ (-2,2)$. As the ![]() $U_n$ dominate the driving term, the assumption 1 is satisfied. And since
$U_n$ dominate the driving term, the assumption 1 is satisfied. And since ![]() $\frac{1}{2} +\frac{1}{2\cdot 3}<\frac{3}{4}$, we expect that
$\frac{1}{2} +\frac{1}{2\cdot 3}<\frac{3}{4}$, we expect that ![]() $X_n\to 0$ holds with positive probability. In Figure 1 we can see a typical example where convergence of the iterates occurs.
$X_n\to 0$ holds with positive probability. In Figure 1 we can see a typical example where convergence of the iterates occurs.

Figure 1. ![]() $(X_n)_{n\geq 10}$ and
$(X_n)_{n\geq 10}$ and ![]() $X_{10}=-1$.
$X_{10}=-1$.
2. Preliminary results
We will now prove two important lemmas that will be needed throughout. Let ![]() $f\,:\,\mathbb{R}\rightarrow \mathbb{R}$ be Lipschitz such that for every
$f\,:\,\mathbb{R}\rightarrow \mathbb{R}$ be Lipschitz such that for every ![]() $\epsilon>0$ there exists c such that
$\epsilon>0$ there exists c such that ![]() $f(x)>c>0$ for all
$f(x)>c>0$ for all ![]() $x \in \mathbb{R}\setminus (-\epsilon,\epsilon) $. Also, let
$x \in \mathbb{R}\setminus (-\epsilon,\epsilon) $. Also, let ![]() $g\,:\,\mathbb{R}_{\geq 0}\rightarrow \mathbb{R}$ be a continuous function such that
$g\,:\,\mathbb{R}_{\geq 0}\rightarrow \mathbb{R}$ be a continuous function such that ![]() $\int_{0}^{\infty} g^2(t) \text{d}t <\infty $. Let
$\int_{0}^{\infty} g^2(t) \text{d}t <\infty $. Let ![]() $X_t$ satisfy
$X_t$ satisfy
Lemma 2.1. ![]() $\limsup_{t \rightarrow \infty} X_t \geq 0 $ a.s.
$\limsup_{t \rightarrow \infty} X_t \geq 0 $ a.s.
Proof. We will argue by contradiction. Assume that ![]() $\limsup_{t \rightarrow \infty} X_t < 0 $, and pick
$\limsup_{t \rightarrow \infty} X_t < 0 $, and pick ![]() $\delta >0 $ such that
$\delta >0 $ such that ![]() $\limsup_{t \rightarrow \infty} X_t< -\delta$ with positive probability. Then there is a time u such that
$\limsup_{t \rightarrow \infty} X_t< -\delta$ with positive probability. Then there is a time u such that ![]() $X_t \leq -\delta$ for all
$X_t \leq -\delta$ for all ![]() $ t\geq u$. But this has as an immediate consequence that
$ t\geq u$. But this has as an immediate consequence that ![]() $\int_{1}^{t} f(X_s) {\rm d}s \rightarrow \infty $. However, since the process
$\int_{1}^{t} f(X_s) {\rm d}s \rightarrow \infty $. However, since the process ![]() $G_t= \int_{1}^{t} g(s) {\rm d}B_s $ has finite quadratic variation, i.e.
$G_t= \int_{1}^{t} g(s) {\rm d}B_s $ has finite quadratic variation, i.e. ![]() $\sup_t \langle G_t \rangle=\int_{0}^{\infty} g^2(s) \text{d}s <\infty$,
$\sup_t \langle G_t \rangle=\int_{0}^{\infty} g^2(s) \text{d}s <\infty$, ![]() $G_t$ stays a.s. finite. The last two observations imply that
$G_t$ stays a.s. finite. The last two observations imply that ![]() $X_t \rightarrow \infty$, which is a contradiction.
$X_t \rightarrow \infty$, which is a contradiction.
Lemma 2.2. ![]() $\liminf_{t \rightarrow \infty} X_t \geq 0 $ a.s.
$\liminf_{t \rightarrow \infty} X_t \geq 0 $ a.s.
Proof. We will again argue by contradiction. Assume that ![]() $\liminf_{t \rightarrow \infty} X_t < 0 $ on a set of positive probability. Take an enumeration of the pairs of positive rationals
$\liminf_{t \rightarrow \infty} X_t < 0 $ on a set of positive probability. Take an enumeration of the pairs of positive rationals ![]() $(q_n,p_n)$ such that
$(q_n,p_n)$ such that ![]() $q_n>p_n$. Now, define
$q_n>p_n$. Now, define ![]() $A_{n}= \{ X_t \leq -q_n \text{\ i.o.}, X_t\geq -p_n \text{\ i.o.} \} $. Since
$A_{n}= \{ X_t \leq -q_n \text{\ i.o.}, X_t\geq -p_n \text{\ i.o.} \} $. Since ![]() $ \limsup_{t \rightarrow \infty} X_t \geq 0 $, we have
$ \limsup_{t \rightarrow \infty} X_t \geq 0 $, we have ![]() $ \bigcup_{n\geq 0} A_{n} = \{ \liminf_{t \rightarrow \infty} X_t < 0 \} $. Now, for
$ \bigcup_{n\geq 0} A_{n} = \{ \liminf_{t \rightarrow \infty} X_t < 0 \} $. Now, for ![]() $ t_1<t_2$ assume that
$ t_1<t_2$ assume that ![]() $ X_{t_1} \geq -p_n $ and
$ X_{t_1} \geq -p_n $ and ![]() $ X_{t_2} \leq -q_n $. Then we see that
$ X_{t_2} \leq -q_n $. Then we see that ![]() $X_{t_2} -X_{t_1} \leq -q_n + p_n $; however,
$X_{t_2} -X_{t_1} \leq -q_n + p_n $; however,
 \begin{align*} X_{t_2} - X_{t_1} &= \int_{t_1}^{t_2} f(X_s) {\rm d} s + \int_{t_1}^{t_2} g(s){\rm d}B_s \\[4pt]
&\geq \int_{t_1}^{t_2} g(s) {\rm d}B_s . \end{align*}
\begin{align*} X_{t_2} - X_{t_1} &= \int_{t_1}^{t_2} f(X_s) {\rm d} s + \int_{t_1}^{t_2} g(s){\rm d}B_s \\[4pt]
&\geq \int_{t_1}^{t_2} g(s) {\rm d}B_s . \end{align*}
Hence we conclude that ![]() $ \int_{t_1}^{t_2} g(s){\rm d}B_s \leq -q_n + p_n$. By the definition of
$ \int_{t_1}^{t_2} g(s){\rm d}B_s \leq -q_n + p_n$. By the definition of ![]() $A_n$, on the event
$A_n$, on the event ![]() $A_n$ we can find a sequence of times
$A_n$ we can find a sequence of times ![]() $(t_{2k}, t_{2k+1})$ such that
$(t_{2k}, t_{2k+1})$ such that ![]() $t_{2k}< t_{2k+1} $ and
$t_{2k}< t_{2k+1} $ and ![]() $ \int_{t_{2k}}^{t_{2k+1}} g(s) {\rm d}B_s \leq -q_n + p_n$. Now, if we define
$ \int_{t_{2k}}^{t_{2k+1}} g(s) {\rm d}B_s \leq -q_n + p_n$. Now, if we define ![]() $G_{u,t} = \int_u ^t g(s) {\rm d}B_s $, we see that
$G_{u,t} = \int_u ^t g(s) {\rm d}B_s $, we see that ![]() $G_{1,t}$ converges a.s. since it is a martingale of bounded quadratic variation. Hence
$G_{1,t}$ converges a.s. since it is a martingale of bounded quadratic variation. Hence ![]() $\mathbb{P} (A_n) =0$, i.e.
$\mathbb{P} (A_n) =0$, i.e. ![]() $\mathbb{P} (\liminf_{t \rightarrow \infty} X_t < 0 )=0$.
$\mathbb{P} (\liminf_{t \rightarrow \infty} X_t < 0 )=0$.
The next comparison result is intuitively obvious; however, it will be useful for comparing processes with different drifts.
Proposition 2.1. Let ![]() $(C_t)_{t\geq 0}$ and
$(C_t)_{t\geq 0}$ and ![]() $(D_t)_{t\geq 0}$ be stochastic processes in the same Wiener space that satisfy
$(D_t)_{t\geq 0}$ be stochastic processes in the same Wiener space that satisfy
respectively, where ![]() $g,f_1,f_2$ are deterministic real-valued functions. Assume that
$g,f_1,f_2$ are deterministic real-valued functions. Assume that ![]() $f_1(x) > f_2( x)$ for all
$f_1(x) > f_2( x)$ for all ![]() $x \in \mathbb{R}$, and
$x \in \mathbb{R}$, and ![]() $C_{s_0}> D_{s_0} $. Then
$C_{s_0}> D_{s_0} $. Then ![]() $C_{t} > D_{t}$ for every
$C_{t} > D_{t}$ for every ![]() $t \geq s_0 $ a.s.
$t \geq s_0 $ a.s.
Proof. Define ![]() $\tau =\inf\{ t> s_0 | C_t= D_t \}$, and set
$\tau =\inf\{ t> s_0 | C_t= D_t \}$, and set ![]() $D_\tau=C_\tau=c$, for
$D_\tau=C_\tau=c$, for ![]() $\tau<\infty$. Now, from continuity of
$\tau<\infty$. Now, from continuity of ![]() $f_1$ and
$f_1$ and ![]() $f_2$, we can find
$f_2$, we can find ![]() $\delta$ such that
$\delta$ such that ![]() $f_1(x) >f_2(x)$ for every
$f_1(x) >f_2(x)$ for every ![]() $x \in ( c-\delta , c ] $. However, for all s we have
$x \in ( c-\delta , c ] $. However, for all s we have
Thus, for s such that ![]() $ C_y, D_y \in (c-\delta,c)$ for every
$ C_y, D_y \in (c-\delta,c)$ for every ![]() $y \in ( s,\tau ) $, we have
$y \in ( s,\tau ) $, we have
 \begin{align*} 0&> -( C_s - D_s ) \\[4pt]
&= \int_ s ^ \tau f_1(C_u) - f_2 ( D_u) {\rm d} u \\[4pt]
&>0. \end{align*}
\begin{align*} 0&> -( C_s - D_s ) \\[4pt]
&= \int_ s ^ \tau f_1(C_u) - f_2 ( D_u) {\rm d} u \\[4pt]
&>0. \end{align*}
Therefore ![]() $ \{\tau<\infty\}$ has zero probability.
$ \{\tau<\infty\}$ has zero probability.
In what follows, we will prove two important lemmas, corresponding to Lemma 2.1 and Lemma 2.2, for the discrete case. We will assume that ![]() $X_n$ satisfies
$X_n$ satisfies
where f has the property that for every ![]() $\epsilon>0$ there exists
$\epsilon>0$ there exists ![]() $c>0$ such that
$c>0$ such that ![]() $f(x)\geq c$ for every
$f(x)\geq c$ for every ![]() $x \in (-\infty,-\epsilon)$, and the
$x \in (-\infty,-\epsilon)$, and the ![]() $Y_n$ are defined similarly as in (5).
$Y_n$ are defined similarly as in (5).
Lemma 2.3. ![]() $\limsup X_n \geq 0$ a.s.
$\limsup X_n \geq 0$ a.s.
Proof. The proof is nearly identical to that of the continuous case (Lemma 2.1).
Lemma 2.4. ![]() $\liminf_{t \rightarrow \infty} X_t \geq 0 $ a.s.
$\liminf_{t \rightarrow \infty} X_t \geq 0 $ a.s.
Proof. The proof is identical to that of the continuous case (Lemma 2.2).
We provide a suitable version of the Borel–Cantelli lemma (for a reference see Theorem 5.3.2 in [Reference DurrettDur13]).
Lemma 2.5. Let ![]() $\mathcal{F}_n$,
$\mathcal{F}_n$, ![]() $n \geq 0$, be a filtration with
$n \geq 0$, be a filtration with ![]() $\mathcal{F}_0 = \{ 0, \Omega \}$, and let
$\mathcal{F}_0 = \{ 0, \Omega \}$, and let ![]() $A_n$,
$A_n$, ![]() $n\geq 1$, be a sequence of events with
$n\geq 1$, be a sequence of events with ![]() $A_n\in \mathcal{F}_n$. Then
$A_n\in \mathcal{F}_n$. Then
 \begin{equation*}\{A_n \mathrm{\,i.o.} \} = \left \{ \sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) = \infty \right \}.\end{equation*}
\begin{equation*}\{A_n \mathrm{\,i.o.} \} = \left \{ \sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) = \infty \right \}.\end{equation*}
3. Continuous model, simplest case
3.1. Introduction
Let ![]() $L_t$ be defined by (4), for
$L_t$ be defined by (4), for ![]() $f(x)=k|x|$ and
$f(x)=k|x|$ and ![]() $\gamma=1$. To simplify, we make a time change and consider
$\gamma=1$. To simplify, we make a time change and consider ![]() $X_t \,{:}\,{\raise-1.5pt{=}}\, L_{e^t}$, and subsequently we obtain
$X_t \,{:}\,{\raise-1.5pt{=}}\, L_{e^t}$, and subsequently we obtain
 \begin{align*}X_{t+{\rm d}t} - X_t &= L_{e^t+e^t {\rm d}t} -L_{e^t}\\&= k|L_{e^t}| {\rm d}t + e^{-t} (B_{t + e^t {\rm d}t} - B_{e^t}) \\&= k|X_t| {\rm d}t + e^{-\frac{t}{2}} {\rm d}B_t,\end{align*}
\begin{align*}X_{t+{\rm d}t} - X_t &= L_{e^t+e^t {\rm d}t} -L_{e^t}\\&= k|L_{e^t}| {\rm d}t + e^{-t} (B_{t + e^t {\rm d}t} - B_{e^t}) \\&= k|X_t| {\rm d}t + e^{-\frac{t}{2}} {\rm d}B_t,\end{align*}
which is the model we will study. We begin with some definitions: first,
We introduce another SDE closely related to the previous one, which will be useful:
It is easy to see that both of these SDEs admit unique strong solutions; for a reference see Theorem 11.2 in Chapter 6 in [Reference Rogers and WilliamsRWW87]. Therefore we can construct ![]() $X_t,K_t$ in the classical Wiener space
$X_t,K_t$ in the classical Wiener space ![]() $(\Omega, \mathcal{F}, \mathbb{P})$. The solution for the SDE (10) is given by
$(\Omega, \mathcal{F}, \mathbb{P})$. The solution for the SDE (10) is given by ![]() $ K_t = e^{ k t} (e^{ -t_0k } K_{t_0} + \int_{t_0}^t e^{-s (k +\frac{1}{2} ) } {\rm d} B_s )$. Indeed, substituting in (10) and using Itô’s formula, we get
$ K_t = e^{ k t} (e^{ -t_0k } K_{t_0} + \int_{t_0}^t e^{-s (k +\frac{1}{2} ) } {\rm d} B_s )$. Indeed, substituting in (10) and using Itô’s formula, we get
 \begin{align*} {\rm d} K_t &= a'(t) (k_0 + \int_{t_0}^{t} b(s) {\rm d} B_s ) + a(t)b(t){\rm d} B_t \\&= \frac{a'(t)}{a(t)} K_t+ a(t)b(t) {\rm d}B_t ,\end{align*}
\begin{align*} {\rm d} K_t &= a'(t) (k_0 + \int_{t_0}^{t} b(s) {\rm d} B_s ) + a(t)b(t){\rm d} B_t \\&= \frac{a'(t)}{a(t)} K_t+ a(t)b(t) {\rm d}B_t ,\end{align*}
where ![]() $ a(t)= e^{ k (t-t_0)} $ and
$ a(t)= e^{ k (t-t_0)} $ and ![]() $ b(t) = e^{-t(\frac{1}{2}+k) +kt_0 }$, so that
$ b(t) = e^{-t(\frac{1}{2}+k) +kt_0 }$, so that ![]() $\frac{a'(t)}{a(t)} = k$ and
$\frac{a'(t)}{a(t)} = k$ and ![]() $ a(t)b(t)= e^{-\frac{t}{2}} $.
$ a(t)b(t)= e^{-\frac{t}{2}} $.
Proposition 3.1. Let ![]() $(X_t)_{t \geq t_0},\,(K_t)_{t \geq t_0}$ in the Wiener probability space
$(X_t)_{t \geq t_0},\,(K_t)_{t \geq t_0}$ in the Wiener probability space ![]() $(\Omega,\mathcal{F},\mathbb{P})$ be the solutions of (9), (10) respectively. We start them at time
$(\Omega,\mathcal{F},\mathbb{P})$ be the solutions of (9), (10) respectively. We start them at time ![]() $t_0$,
$t_0$, ![]() $ X_{t_0} \geq K_{t_0} \geq 0$. Then
$ X_{t_0} \geq K_{t_0} \geq 0$. Then ![]() $ X_t \geq K_t$ for every
$ X_t \geq K_t$ for every ![]() $t\geq t_0 $.
$t\geq t_0 $.
Proof. This is a direct application of Proposition 2.1.
3.2. Analysis of  $\textbf{\textit{X}}_{\textbf{\textit{t}}}$ when
$\textbf{\textit{X}}_{\textbf{\textit{t}}}$ when  $k>1/2$
$k>1/2$
We start by stating the main result of this section, which we will prove at the end of the subsection.
Theorem 3.1. Let ![]() $(X_t)_{t\geq 1}$ be the solution of (9) for
$(X_t)_{t\geq 1}$ be the solution of (9) for ![]() $k>\frac{1}{2}$; then
$k>\frac{1}{2}$; then ![]() $X_t \rightarrow \infty$ a.s.
$X_t \rightarrow \infty$ a.s.
Now we will show that ![]() $(X_t)_{t\geq 1}$ cannot stay negative for all times. This will be accomplished by a direct computation after solving the SDE.
$(X_t)_{t\geq 1}$ cannot stay negative for all times. This will be accomplished by a direct computation after solving the SDE.
Proposition 3.2. Let ![]() $(X_t)_{t\geq 1}$ be the solution of (9) for
$(X_t)_{t\geq 1}$ be the solution of (9) for ![]() $k>\frac{1}{2}$. Assume that at time s,
$k>\frac{1}{2}$. Assume that at time s, ![]() $X_{s} < 0 $. Then
$X_{s} < 0 $. Then ![]() $X_t$ will reach 0 with probability 1, i.e.
$X_t$ will reach 0 with probability 1, i.e. ![]() $\mathbb{P}( \sup_{u\geq s} X_u > 0 )=1$.
$\mathbb{P}( \sup_{u\geq s} X_u > 0 )=1$.
Proof. First, note that the solution of the SDE (9), run from time s with initial condition ![]() $X_{s}<0$, coincides with the solution of the SDE
$X_{s}<0$, coincides with the solution of the SDE ![]() $ {\rm d}X_t = -k X_t {\rm d}t + e^{-\frac{t}{2}}{\rm d} B_t $ before
$ {\rm d}X_t = -k X_t {\rm d}t + e^{-\frac{t}{2}}{\rm d} B_t $ before ![]() $X_t$ hits 0. Formally, we define
$X_t$ hits 0. Formally, we define ![]() $\tau_0 = \inf \{ t| t \geq s,\,X_t=0 \}$. Using the same method as when solving SDE (10), we obtain
$\tau_0 = \inf \{ t| t \geq s,\,X_t=0 \}$. Using the same method as when solving SDE (10), we obtain ![]() $X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $ on
$X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $ on ![]() $\{t <\tau_0 \}$. Set
$\{t <\tau_0 \}$. Set ![]() $G_t= \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u $, and calculate the quadratic variation of
$G_t= \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u $, and calculate the quadratic variation of ![]() $G_t$, namely
$G_t$, namely ![]() $\left \langle G_t \right \rangle = ( e^{2t(k-\frac{1}{2}) } -e^{2s(k-\frac{1}{2}) } )/(2k-1) $. Next, we compute the probability of never returning to zero:
$\left \langle G_t \right \rangle = ( e^{2t(k-\frac{1}{2}) } -e^{2s(k-\frac{1}{2}) } )/(2k-1) $. Next, we compute the probability of never returning to zero:
 \begin{align*}\mathbb{P}(\tau =\infty) & = \mathbb{P}\left(\sup_{s \lt u \lt \infty} X_u \leq 0 \right)\\[6pt]
& = \mathbb{P}\left(\sup_{s \lt u \lt \infty} G_u \leq-e^{ks} X_{s} \right)\\[6pt]
&= 1- \mathbb{P}\left(\sup_{s \lt u \lt \infty} G_u \gt -e^{ks} X_{s} \right) \\[6pt]
&=1- \lim_{t\rightarrow \infty}\mathbb{P}\left(\sup_{s \lt u \lt t} G_u \gt -e^{ks} X_{s} \right) \\[6pt]
&= 1- \lim_{t\rightarrow \infty}2 \mathbb{P}\left( G_t \gt -e^{ks} X_{s}\right), \textrm{from\,the\,reflection\,principle} \\[6pt]
&= 1- \lim_{t\rightarrow \infty}2 \mathbb{P}\left(N\left( 0, \frac{e^{2t(k-\frac{1}{2})}-e^{2s(k-\frac{1}{2})}}{2k -1} \right) \gt -e^{ks} X_{s} \right) \\[4pt]
&=0,\end{align*}
\begin{align*}\mathbb{P}(\tau =\infty) & = \mathbb{P}\left(\sup_{s \lt u \lt \infty} X_u \leq 0 \right)\\[6pt]
& = \mathbb{P}\left(\sup_{s \lt u \lt \infty} G_u \leq-e^{ks} X_{s} \right)\\[6pt]
&= 1- \mathbb{P}\left(\sup_{s \lt u \lt \infty} G_u \gt -e^{ks} X_{s} \right) \\[6pt]
&=1- \lim_{t\rightarrow \infty}\mathbb{P}\left(\sup_{s \lt u \lt t} G_u \gt -e^{ks} X_{s} \right) \\[6pt]
&= 1- \lim_{t\rightarrow \infty}2 \mathbb{P}\left( G_t \gt -e^{ks} X_{s}\right), \textrm{from\,the\,reflection\,principle} \\[6pt]
&= 1- \lim_{t\rightarrow \infty}2 \mathbb{P}\left(N\left( 0, \frac{e^{2t(k-\frac{1}{2})}-e^{2s(k-\frac{1}{2})}}{2k -1} \right) \gt -e^{ks} X_{s} \right) \\[4pt]
&=0,\end{align*}
since
We will now prove two important lemmas that are true for solutions of (9) for any ![]() $k>0.$
$k>0.$
Lemma 3.1. Let ![]() $(X_t)_{t\geq 1}$ be the solution of (9). Then on the event
$(X_t)_{t\geq 1}$ be the solution of (9). Then on the event ![]() $\{X_t \geq 0 \text{\ i.o.} \}$, there is a positive constant
$\{X_t \geq 0 \text{\ i.o.} \}$, there is a positive constant ![]() $c<1$ such that
$c<1$ such that ![]() $\{ X_t \geq c e^{-t/2} \text{\ i.o.} \}$ holds a.s.
$\{ X_t \geq c e^{-t/2} \text{\ i.o.} \}$ holds a.s.
Proof. Assume we start the SDE at time ![]() $t_i$ with initial condition
$t_i$ with initial condition ![]() $X_{t_i}\geq 0$. Then we see that
$X_{t_i}\geq 0$. Then we see that
Set ![]() $G_t =\int_{t_i}^t e^{-\frac{u}{2}} {\rm d}B_u$. The quadratic variation of
$G_t =\int_{t_i}^t e^{-\frac{u}{2}} {\rm d}B_u$. The quadratic variation of ![]() $G_t$ is
$G_t$ is ![]() $\langle G_t\rangle = e^{-t_1} - e^{-t}$. Fix
$\langle G_t\rangle = e^{-t_1} - e^{-t}$. Fix ![]() $0<c<1$. Now, observe that we can always choose t big enough so that
$0<c<1$. Now, observe that we can always choose t big enough so that ![]() $\langle G_t \rangle \geq c e^{-t_1}$ for any
$\langle G_t \rangle \geq c e^{-t_1}$ for any ![]() $t_1$.
$t_1$.
Then
 \begin{align*}\mathbb{P} \Big( \sup _{t_i<u<t }X_u >e^{-t_1/2 } \Big) &\geq \mathbb{P} \Big( \sup _{t_i<u<t }G_u >e^{-t_1/2 } \Big) \\[4pt]
&= 2\mathbb{P} \big( G_t \gt e^{-t_1/2 } \big) \\[4pt]
& \geq 2\mathbb{P} \big( N(0,c e^{-t_1}) \gt e^{-t_1/2 } \big) \\[4pt]
& = 2\mathbb{P} \big( N(0, c) \gt 1 \big) \gt \gamma \gt 0.\end{align*}
\begin{align*}\mathbb{P} \Big( \sup _{t_i<u<t }X_u >e^{-t_1/2 } \Big) &\geq \mathbb{P} \Big( \sup _{t_i<u<t }G_u >e^{-t_1/2 } \Big) \\[4pt]
&= 2\mathbb{P} \big( G_t \gt e^{-t_1/2 } \big) \\[4pt]
& \geq 2\mathbb{P} \big( N(0,c e^{-t_1}) \gt e^{-t_1/2 } \big) \\[4pt]
& = 2\mathbb{P} \big( N(0, c) \gt 1 \big) \gt \gamma \gt 0.\end{align*}
Let ![]() $ g(x) = \inf \{ y| e^{-x} - e^{-y} \geq c e^{-x} \}$. Now we can formally define the sequence of the stopping times. The first stopping time is
$ g(x) = \inf \{ y| e^{-x} - e^{-y} \geq c e^{-x} \}$. Now we can formally define the sequence of the stopping times. The first stopping time is ![]() $\tau_1 = \inf \{t |X_{t} \geq 0 \} $; then we define recursively
$\tau_1 = \inf \{t |X_{t} \geq 0 \} $; then we define recursively ![]() $\tau_{i+1} = \inf \{ t | t> \tau_i, t> g(\tau_i), \, X_t \geq 0 \}$. We also define the associated filtration
$\tau_{i+1} = \inf \{ t | t> \tau_i, t> g(\tau_i), \, X_t \geq 0 \}$. We also define the associated filtration ![]() $ \mathcal{F}_n = \mathcal{F}_{ \tau_n}$, for
$ \mathcal{F}_n = \mathcal{F}_{ \tau_n}$, for ![]() $n\geq 1$ and
$n\geq 1$ and ![]() $\mathcal{F}_0 =\{ 0 , \Omega \}$. Now let
$\mathcal{F}_0 =\{ 0 , \Omega \}$. Now let ![]() $ A_n =\{ \exists t,\, \tau_{n-1} <t< \tau_{n} \, , \text{ s.t.\ } X_t \geq c e^{- t/2} \}$. By definition
$ A_n =\{ \exists t,\, \tau_{n-1} <t< \tau_{n} \, , \text{ s.t.\ } X_t \geq c e^{- t/2} \}$. By definition ![]() $A_n \in \mathcal{F}_n$. We find a lower bound for
$A_n \in \mathcal{F}_n$. We find a lower bound for ![]() $ \mathbb{P} (A_n | \mathcal{F}_{n-1} )$:
$ \mathbb{P} (A_n | \mathcal{F}_{n-1} )$:
 \begin{align*}\mathbb{P} (A_n | \mathcal{F}_{n-1}) & \geq \mathbb{P} \Big( \sup_{\tau_{n-1} \lt u \lt \tau_n} X_u \gt ce^{-t_{n-1} /2} | \mathcal{F}_{n-1} \Big) \\
&\geq \mathbb{P} \Big( \sup_{\tau_{n-1} \lt u \lt g(\tau_{ n-1})} X_u \gt ce^{-\tau_{n-1} /2} | \mathcal{F}_{n-1}\Big) \\
& \gt \gamma .\end{align*}
\begin{align*}\mathbb{P} (A_n | \mathcal{F}_{n-1}) & \geq \mathbb{P} \Big( \sup_{\tau_{n-1} \lt u \lt \tau_n} X_u \gt ce^{-t_{n-1} /2} | \mathcal{F}_{n-1} \Big) \\
&\geq \mathbb{P} \Big( \sup_{\tau_{n-1} \lt u \lt g(\tau_{ n-1})} X_u \gt ce^{-\tau_{n-1} /2} | \mathcal{F}_{n-1}\Big) \\
& \gt \gamma .\end{align*}
On ![]() $\{X_t\geq 0 \text{\ i.o.}\}$ the sum
$\{X_t\geq 0 \text{\ i.o.}\}$ the sum ![]() $\sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) $ has infinitely many nonzero terms bigger than
$\sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) $ has infinitely many nonzero terms bigger than ![]() $\gamma$; hence
$\gamma$; hence ![]() $\sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) = \infty $ a.s. Finally, by Lemma 2.5 (Borel–Cantelli) we conclude.
$\sum_{n\geq 1} \mathbb{P}(A_n | \mathcal{F}_{n-1} ) = \infty $ a.s. Finally, by Lemma 2.5 (Borel–Cantelli) we conclude.
The next lemma uses the previous lemma to establish that on ![]() $\{X_t \geq 0 \text{\ i.o.} \}$ we have
$\{X_t \geq 0 \text{\ i.o.} \}$ we have ![]() $\liminf_{t \rightarrow \infty} X_t >0 $.
$\liminf_{t \rightarrow \infty} X_t >0 $.
Lemma 3.2. Let ![]() $(X_t)_{t\geq 1}$ be the solution of (9). Then on the event
$(X_t)_{t\geq 1}$ be the solution of (9). Then on the event ![]() $\{X_t \geq 0 \text{\ i.o.} \}$ we have that
$\{X_t \geq 0 \text{\ i.o.} \}$ we have that ![]() $\{\liminf_{t \rightarrow \infty} X_t >0 \}$ holds a.s.
$\{\liminf_{t \rightarrow \infty} X_t >0 \}$ holds a.s.
Proof. Indeed, if we start the process at time s with initial condition ![]() $X_{s} \geq ce^{- \frac{s}{2}}$, then the solution of (9), before hitting 0, is given by
$X_{s} \geq ce^{- \frac{s}{2}}$, then the solution of (9), before hitting 0, is given by
Define ![]() $G_t=\int_{s}^{t} e^{-s(k+\frac{1}{2}) } {\rm d}B_s $. We calculate its quadratic variation:
$G_t=\int_{s}^{t} e^{-s(k+\frac{1}{2}) } {\rm d}B_s $. We calculate its quadratic variation:
Taking ![]() $ t \rightarrow \infty $ shows
$ t \rightarrow \infty $ shows ![]() $\langle G_{\infty }\rangle= \dfrac{ e^{-2sk-s} }{2k+1 }$. Therefore,
$\langle G_{\infty }\rangle= \dfrac{ e^{-2sk-s} }{2k+1 }$. Therefore,
 \begin{align}\mathbb{P} \left(\inf_{s \leq u <\infty } X_u >\frac{c}{2}e^{ -\frac{s}{2} } \right)&=\mathbb{P} \left(\inf_{s \leq u <\infty } e^{ku}\left(ce^{-s\left(k +\frac{1}{2}\right)} + G_u \right) > \frac{c}{2}e^{ -\frac{s}{2} } \right)\nonumber\\[4pt]
&\geq \mathbb{P} \left(\inf_{s \leq u <\infty } e^{ks}\left(ce^{-s\left(k +\frac{1}{2}\right)} + G_u \right) > \frac{c}{2}e^{ -\frac{s}{2} } \right)\nonumber \\[4pt]
&=\mathbb{P} \left(\inf_{s \leq u <\infty } ce^{-s\left(k +\frac{1}{2}\right)} + G_u > \frac{c}{2}e^{ -s\left(k +\frac{1}{2}\right) } \right)\nonumber \\[4pt]
&=\mathbb{P} \left(\inf_{s \leq u <\infty } G_u > -\frac{c}{2}e^{ -s\left(k +\frac{1}{2} \right)} \right)\\[4pt]
&= 1- \mathbb{P} \left(\sup_{s \leq u <\infty } G_u >\frac{c}{2}e^{ - s\left(k +\frac{1}{2} \right) } \right)\nonumber \\[4pt]
&= 1-2\lim_{t\rightarrow \infty} \mathbb{P} \left(G_t>-\frac{c}{2}e^{ -s\left(k +\frac{1}{2}\right) } \right),\text{ by\,the\,reflection\,principle} \nonumber\\[4pt]
&=1-2\mathbb{P} \left(N\left(0, \dfrac{ e^{-s(2k+1)} }{2k+1 }\right) > \frac{c}{2}e^{ -s(k +\frac{1}{2} ) } \right)\nonumber \\[4pt]
&=1-2\mathbb{P}\left(N\left(0,\frac{1}{k+1}\right) > \frac{c}{2} \right)>\delta>0. \nonumber\end{align}
\begin{align}\mathbb{P} \left(\inf_{s \leq u <\infty } X_u >\frac{c}{2}e^{ -\frac{s}{2} } \right)&=\mathbb{P} \left(\inf_{s \leq u <\infty } e^{ku}\left(ce^{-s\left(k +\frac{1}{2}\right)} + G_u \right) > \frac{c}{2}e^{ -\frac{s}{2} } \right)\nonumber\\[4pt]
&\geq \mathbb{P} \left(\inf_{s \leq u <\infty } e^{ks}\left(ce^{-s\left(k +\frac{1}{2}\right)} + G_u \right) > \frac{c}{2}e^{ -\frac{s}{2} } \right)\nonumber \\[4pt]
&=\mathbb{P} \left(\inf_{s \leq u <\infty } ce^{-s\left(k +\frac{1}{2}\right)} + G_u > \frac{c}{2}e^{ -s\left(k +\frac{1}{2}\right) } \right)\nonumber \\[4pt]
&=\mathbb{P} \left(\inf_{s \leq u <\infty } G_u > -\frac{c}{2}e^{ -s\left(k +\frac{1}{2} \right)} \right)\\[4pt]
&= 1- \mathbb{P} \left(\sup_{s \leq u <\infty } G_u >\frac{c}{2}e^{ - s\left(k +\frac{1}{2} \right) } \right)\nonumber \\[4pt]
&= 1-2\lim_{t\rightarrow \infty} \mathbb{P} \left(G_t>-\frac{c}{2}e^{ -s\left(k +\frac{1}{2}\right) } \right),\text{ by\,the\,reflection\,principle} \nonumber\\[4pt]
&=1-2\mathbb{P} \left(N\left(0, \dfrac{ e^{-s(2k+1)} }{2k+1 }\right) > \frac{c}{2}e^{ -s(k +\frac{1}{2} ) } \right)\nonumber \\[4pt]
&=1-2\mathbb{P}\left(N\left(0,\frac{1}{k+1}\right) > \frac{c}{2} \right)>\delta>0. \nonumber\end{align}
We know that on ![]() $\{X_t\geq 0 \text{\ i.o.}\}$ the event
$\{X_t\geq 0 \text{\ i.o.}\}$ the event ![]() $\{X_t\geq c e^{-\frac{t}{2}} \text{\ i.o.} \}$ holds a.s. Therefore, on
$\{X_t\geq c e^{-\frac{t}{2}} \text{\ i.o.} \}$ holds a.s. Therefore, on ![]() $\{X_t\geq 0 \text{\ i.o.}\}$, if we define
$\{X_t\geq 0 \text{\ i.o.}\}$, if we define ![]() $\tau_0=0$ and
$\tau_0=0$ and ![]() $\tau_{n+1} = \{t>\tau_n+1| X_t \geq c e^{-\frac{t}{2}} \}$, we see that
$\tau_{n+1} = \{t>\tau_n+1| X_t \geq c e^{-\frac{t}{2}} \}$, we see that ![]() $\tau_n<\infty$ a.s., and
$\tau_n<\infty$ a.s., and ![]() $\tau_n \rightarrow \infty$ a.s. Also, we define the corresponding filtration, namely
$\tau_n \rightarrow \infty$ a.s. Also, we define the corresponding filtration, namely ![]() $\mathcal{F}_n = \sigma( \tau_n)$.
$\mathcal{F}_n = \sigma( \tau_n)$.
To show that on the event ![]() $\{X_t\geq c e^{-\frac{t}{2}} \text{\ i.o.}\}$ the event
$\{X_t\geq c e^{-\frac{t}{2}} \text{\ i.o.}\}$ the event ![]() $A=\{\liminf_{\rightarrow \infty} X_t\leq 0\}$ has probability zero, it suffices to argue that there is a
$A=\{\liminf_{\rightarrow \infty} X_t\leq 0\}$ has probability zero, it suffices to argue that there is a ![]() $\delta$ such that
$\delta$ such that ![]() $ \mathbb{P}( A|\mathcal{F}_n )<1-\delta$ a.s. for all
$ \mathbb{P}( A|\mathcal{F}_n )<1-\delta$ a.s. for all ![]() $n\geq 1$. This is immediate from the previous calculation. Indeed,
$n\geq 1$. This is immediate from the previous calculation. Indeed,
 \begin{align*}\mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P} \left(\inf_{ \tau_{n}\leq u <\infty } X_u >\frac{c}{2}e^{ -\frac{\tau_n}{2} } |\mathcal{F}_n \right)\\&<1-\delta.\end{align*}
\begin{align*}\mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P} \left(\inf_{ \tau_{n}\leq u <\infty } X_u >\frac{c}{2}e^{ -\frac{\tau_n}{2} } |\mathcal{F}_n \right)\\&<1-\delta.\end{align*}
Now we can prove Theorem 3.1.
Proof of Theorem 3.1. From Proposition 3.2 we know that ![]() $\{X_t\geq 0 \text{\ i.o.} \}$ has probability 1. Therefore from Lemma 3.2 we deduce
$\{X_t\geq 0 \text{\ i.o.} \}$ has probability 1. Therefore from Lemma 3.2 we deduce ![]() $\liminf_{t \rightarrow \infty} X_t >0$ a.s. Consequently,
$\liminf_{t \rightarrow \infty} X_t >0$ a.s. Consequently, ![]() $ \int_{0}^\infty |X_u| { \rm d} u \rightarrow \infty$ a.s. At the same time
$ \int_{0}^\infty |X_u| { \rm d} u \rightarrow \infty$ a.s. At the same time ![]() $ \limsup_{t \rightarrow \infty} \int_{0}^{t} e^{-\frac{u}{2}} {\rm d } B_u < \infty$ a.s.; hence
$ \limsup_{t \rightarrow \infty} \int_{0}^{t} e^{-\frac{u}{2}} {\rm d } B_u < \infty$ a.s.; hence ![]() $X_t\rightarrow \infty$ a.s.
$X_t\rightarrow \infty$ a.s.
3.3. Analysis of  $X_t$ when
$X_t$ when  $k<1/2$
$k<1/2$
As before, ![]() $(X_t)_{t\geq 1}$ is the solution of the stochastic differential equation
$(X_t)_{t\geq 1}$ is the solution of the stochastic differential equation ![]() $dX_t= k |X_t|\rm{d}t +e^{-\frac{t}{2}} \text{d}B_t $.
$dX_t= k |X_t|\rm{d}t +e^{-\frac{t}{2}} \text{d}B_t $.
The behavior of ![]() $X_t$ when
$X_t$ when ![]() $k<1/2$ is different. The process in this regime can converge to 0 with positive probability. More specifically, we have the following theorem.
$k<1/2$ is different. The process in this regime can converge to 0 with positive probability. More specifically, we have the following theorem.
Theorem 3.2. Let ![]() $(X_t)_{t \geq 1}$ solve (9) with
$(X_t)_{t \geq 1}$ solve (9) with ![]() $k<\frac{1}{2}$, and define
$k<\frac{1}{2}$, and define ![]() $A= \{X_t\rightarrow 0 \}$,
$A= \{X_t\rightarrow 0 \}$, ![]() $B=\{X_t\rightarrow \infty \}$. Then the following hold:
$B=\{X_t\rightarrow \infty \}$. Then the following hold:
1. Let A, B be as above. Then
 $\mathbb{P}( A\cup B)=1$.
$\mathbb{P}( A\cup B)=1$.2. Both A and B are nontrivial, i.e.,
 $\mathbb{P}(A) >0$ and
$\mathbb{P}(A) >0$ and  $\mathbb{P}(B) >0$.
$\mathbb{P}(B) >0$.3. On
 $\{X_t\geq 0 \mathrm{i.o.} \} $ we get
$\{X_t\geq 0 \mathrm{i.o.} \} $ we get  $X_t\rightarrow \infty.$
$X_t\rightarrow \infty.$
Before proving the theorem, we first need to prove a proposition. We will show that the process, starting from a negative value, will never cross 0 with positive probability.
Proposition 3.3. Let ![]() $(X_t)_{t \geq 1}$ solve (9) with
$(X_t)_{t \geq 1}$ solve (9) with ![]() $k<\frac{1}{2}$. Assume that at time s,
$k<\frac{1}{2}$. Assume that at time s, ![]() $X_{s} < 0 $. Then
$X_{s} < 0 $. Then ![]() $(X_t)_{t \geq 1}$ will hit 0 with probability
$(X_t)_{t \geq 1}$ will hit 0 with probability ![]() $\alpha$, where
$\alpha$, where ![]() $0<\alpha<1$.
$0<\alpha<1$.
Proof. Define the stopping time ![]() $\tau_1 =\inf\{ t\geq s| X_t =0 \}$. As in Proposition 3.2, the solution for
$\tau_1 =\inf\{ t\geq s| X_t =0 \}$. As in Proposition 3.2, the solution for ![]() $X_t$ started at time s up to time
$X_t$ started at time s up to time ![]() $\tau_1$ is given by
$\tau_1$ is given by ![]() $X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $. We have
$X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $. We have
 \begin{align*}\mathbb{P}( \tau =\infty )&= \mathbb{P}\Big( \sup_{ s <u <\infty } X_u \leq 0 \Big)\\
&= 1-\lim_{t\rightarrow \infty }2 \mathbb{P}\Bigg( N\Bigg( 0, \frac{ e^{2t(k-\frac{1}{2}) } -e^{2t(k-\frac{1}{2}) } }{2k -1 } \Bigg) >-e^{ks} X_{s}\Bigg),\text{ as\,in\,Proposition\,} \linkref{pro3.2}{3.2} \\
&= 1- 2 \mathbb{P}\big( N\big( 0, -e^{2s(k-\frac{1}{2}) } /(2k-1) \big) >-e^{ks} X_{s}\big)\\&=1-\alpha.\end{align*}
\begin{align*}\mathbb{P}( \tau =\infty )&= \mathbb{P}\Big( \sup_{ s <u <\infty } X_u \leq 0 \Big)\\
&= 1-\lim_{t\rightarrow \infty }2 \mathbb{P}\Bigg( N\Bigg( 0, \frac{ e^{2t(k-\frac{1}{2}) } -e^{2t(k-\frac{1}{2}) } }{2k -1 } \Bigg) >-e^{ks} X_{s}\Bigg),\text{ as\,in\,Proposition\,} \linkref{pro3.2}{3.2} \\
&= 1- 2 \mathbb{P}\big( N\big( 0, -e^{2s(k-\frac{1}{2}) } /(2k-1) \big) >-e^{ks} X_{s}\big)\\&=1-\alpha.\end{align*}
Therefore ![]() $0<\alpha<1$.
$0<\alpha<1$.
Proof of Theorem 3.2.
1. Define the events
 $N=\{ \exists s \text{s.t. } X_t <0 \forall t\geq s \}$ and
$N=\{ \exists s \text{s.t. } X_t <0 \forall t\geq s \}$ and  $P=\{X_t \geq 0 \text{\ i.o.} \}$. Of course N and P are disjoint and
$P=\{X_t \geq 0 \text{\ i.o.} \}$. Of course N and P are disjoint and  $\mathbb{P}(P \cup N )=1$. To prove Part
$\mathbb{P}(P \cup N )=1$. To prove Part  $\textit{1}$, we will show that
$\textit{1}$, we will show that  $N\subset \{ X_t \rightarrow 0 \}$ up to a null set and
$N\subset \{ X_t \rightarrow 0 \}$ up to a null set and  $P= \{ X_t \rightarrow \infty \} $. From Lemma 2.2 we know that
$P= \{ X_t \rightarrow \infty \} $. From Lemma 2.2 we know that  $\liminf_{t\rightarrow \infty} X_{t}\geq 0$ a.s.; therefore
$\liminf_{t\rightarrow \infty} X_{t}\geq 0$ a.s.; therefore  $N\subset \{X_t\rightarrow 0 \}$ up to a null set.
$N\subset \{X_t\rightarrow 0 \}$ up to a null set.To show that
 $P= \{ X_t \rightarrow \infty \} $, note that Lemma 3.2 shows that on
$P= \{ X_t \rightarrow \infty \} $, note that Lemma 3.2 shows that on  $\{ X_t \geq 0 \text{\ i.o.} \} $,
$\{ X_t \geq 0 \text{\ i.o.} \} $,  $\liminf_{t \rightarrow \infty }X_t >0$ a.s. Consequently, on
$\liminf_{t \rightarrow \infty }X_t >0$ a.s. Consequently, on  $\{X_t \geq 0 \text{\ i.o.}\}$ we have
$\{X_t \geq 0 \text{\ i.o.}\}$ we have  $X_t\to \infty $, as
$X_t\to \infty $, as  $ \int_{0}^\infty |X_u| { \rm d} u \rightarrow \infty$ and
$ \int_{0}^\infty |X_u| { \rm d} u \rightarrow \infty$ and  $ \limsup_{t \rightarrow \infty} \int_{0}^{t} e^{-\frac{u}{2}} {\rm d } B_u < \infty$ a.s. Therefore,
$ \limsup_{t \rightarrow \infty} \int_{0}^{t} e^{-\frac{u}{2}} {\rm d } B_u < \infty$ a.s. Therefore,  $P= \{ X_t \rightarrow \infty \} $, which concludes Part
$P= \{ X_t \rightarrow \infty \} $, which concludes Part  $\textit{1}$.
$\textit{1}$.-
2. The fact that
 $\mathbb{P}(A)>0$ follows immediately from Proposition 3.3. Now, we will prove that
$\mathbb{P}(A)>0$ follows immediately from Proposition 3.3. Now, we will prove that  $\mathbb{P}(B)>0$. Define the stopping time
$\mathbb{P}(B)>0$. Define the stopping time  $\tau_0=\inf\{t |X_t=0 \}$. Also, define
$\tau_0=\inf\{t |X_t=0 \}$. Also, define  $Y(t,\omega)=1$ if
$Y(t,\omega)=1$ if  $X_s\geq 0$ for all
$X_s\geq 0$ for all  $s\geq t+1$. Observe that
$s\geq t+1$. Observe that  $\{ Y_{\tau_0}=1, \tau_0 < \infty \} \subset P $. Hence, using the strong Markov property,
$\{ Y_{\tau_0}=1, \tau_0 < \infty \} \subset P $. Hence, using the strong Markov property,
 \begin{align*} \mathbb{P}(Y_{\tau}=1, \tau
< \infty ) &= \int_{0}^{\infty} \mathbb{ P} ( \tau=u ) \mathbb{P}_0 ( X_t\geq 0, \forall t\geq 1 ){\rm d} u\\ &\geq \int_{0}^{\infty} \mathbb{ P} ( \tau=u ) \mathbb{P}_0 ( K_t\geq 0, \forall t\geq 1 ){\rm d} u \quad \text{\,since\,}\,X_t\geq K_t\\ &=\alpha \mathbb{P}_0 ( K_t\geq 0, \forall t\geq 1 ) \\ &>0. \end{align*}
\begin{align*} \mathbb{P}(Y_{\tau}=1, \tau
< \infty ) &= \int_{0}^{\infty} \mathbb{ P} ( \tau=u ) \mathbb{P}_0 ( X_t\geq 0, \forall t\geq 1 ){\rm d} u\\ &\geq \int_{0}^{\infty} \mathbb{ P} ( \tau=u ) \mathbb{P}_0 ( K_t\geq 0, \forall t\geq 1 ){\rm d} u \quad \text{\,since\,}\,X_t\geq K_t\\ &=\alpha \mathbb{P}_0 ( K_t\geq 0, \forall t\geq 1 ) \\ &>0. \end{align*}
-
3. This follows immediately from the proof of
 $\textit{1}$.
$\textit{1}$.
Lastly, we prove a proposition that will be used in Section 5.
Proposition 3.4. Suppose ![]() $(X_t)_{t\geq 1}$,
$(X_t)_{t\geq 1}$, ![]() $(Y_t)_{t \geq 1}$ solve (9), with constants k and
$(Y_t)_{t \geq 1}$ solve (9), with constants k and ![]() $k_1$ respectively. Suppose that
$k_1$ respectively. Suppose that ![]() $0<k_1<k<1/2$. Let
$0<k_1<k<1/2$. Let ![]() $\epsilon >0$. If
$\epsilon >0$. If ![]() $X_s,Y_s \in(-2\epsilon,-\epsilon)$ a.s., then there is an event A with positive probability, such that
$X_s,Y_s \in(-2\epsilon,-\epsilon)$ a.s., then there is an event A with positive probability, such that ![]() $X_t,Y_t\in (-3\epsilon,0)$ for every
$X_t,Y_t\in (-3\epsilon,0)$ for every ![]() $t>s$.
$t>s$.
Proof. Solving the SDE before it hits zero, we find ![]() $X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $ and
$X_t =e^{-kt} (e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u ) $ and ![]() $Y_t =e^{-k_1t} (e^{k_1s} Y_{s} + \int_{s}^{t} e^{u(k_1-\frac{1}{2}) } {\rm d}B_u ) $. Let
$Y_t =e^{-k_1t} (e^{k_1s} Y_{s} + \int_{s}^{t} e^{u(k_1-\frac{1}{2}) } {\rm d}B_u ) $. Let ![]() $\epsilon >0$. Since the process
$\epsilon >0$. Since the process ![]() $G_{t}=\int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u $ has finite quadratic variation, the event
$G_{t}=\int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u $ has finite quadratic variation, the event ![]() $A=\{G_{t}\in(-\epsilon,\epsilon) \forall t>s \}$ has positive probability. Set
$A=\{G_{t}\in(-\epsilon,\epsilon) \forall t>s \}$ has positive probability. Set ![]() $\tilde{G}_{t}=\int_{s}^{t} e^{u(k_1-\frac{1}{2}) } {\rm d}B_u $, and define
$\tilde{G}_{t}=\int_{s}^{t} e^{u(k_1-\frac{1}{2}) } {\rm d}B_u $, and define ![]() $N_t= G_te^{t(k_1-k)}$. Using Itô’s formula, we find
$N_t= G_te^{t(k_1-k)}$. Using Itô’s formula, we find ![]() $\text{d}N_t=e^{t(k-\frac{1}{2})} e^{(k_1-k) t} \text{d}B_t+ (k_1-k)e^{(k_1-k) t}G_t\text{d}t$. Therefore,
$\text{d}N_t=e^{t(k-\frac{1}{2})} e^{(k_1-k) t} \text{d}B_t+ (k_1-k)e^{(k_1-k) t}G_t\text{d}t$. Therefore,
So
To bound ![]() $|\tilde{G}_t|$ observe that
$|\tilde{G}_t|$ observe that
 \begin{align*}-\int_{s}^t (k_1-k)e^{(k_1-k) u} G_u\text{d}u &\leq -\epsilon \int_{s}^t (k_1-k)e^{(k_1-k) u} \text{d}u\\[4pt]
&=-\epsilon \left(e^{(k_1-k) t}- e^{(k_1-k) s}\right).\end{align*}
\begin{align*}-\int_{s}^t (k_1-k)e^{(k_1-k) u} G_u\text{d}u &\leq -\epsilon \int_{s}^t (k_1-k)e^{(k_1-k) u} \text{d}u\\[4pt]
&=-\epsilon \left(e^{(k_1-k) t}- e^{(k_1-k) s}\right).\end{align*}
Similarly we obtain ![]() $-\int_{s}^t (k_1-k)e^{(k_1-k) u} G_u\text{d}u \geq \epsilon( e^{(k_1-k) t}- e^{(k_1-k) s})$. Thus on A, we obtain the following inequalities:
$-\int_{s}^t (k_1-k)e^{(k_1-k) u} G_u\text{d}u \geq \epsilon( e^{(k_1-k) t}- e^{(k_1-k) s})$. Thus on A, we obtain the following inequalities:
Simplifying, we obtain ![]() $ | \tilde{G}_t | \leq \epsilon e^{(k_1-k) s}\leq \epsilon$. Now we will estimate
$ | \tilde{G}_t | \leq \epsilon e^{(k_1-k) s}\leq \epsilon$. Now we will estimate ![]() $X_t$ on A. Using that
$X_t$ on A. Using that ![]() $\epsilon<|e^{ks}X_s| $ we obtain the upper bound
$\epsilon<|e^{ks}X_s| $ we obtain the upper bound
 \begin{align*}X_t &= e^{-kt} \left(e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u \right ) \\[4pt]
&\leq e^{-kt} (e^{ks} X_{s} +\epsilon )\\[4pt]
&<0\end{align*}
\begin{align*}X_t &= e^{-kt} \left(e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u \right ) \\[4pt]
&\leq e^{-kt} (e^{ks} X_{s} +\epsilon )\\[4pt]
&<0\end{align*}
and the lower bound
 \begin{align*}X_t &= e^{-kt} \left(e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u \right) \\[4pt]
&\geq e^{-kt} (-2e^{ks} \epsilon -\epsilon )\\[4pt]
&\geq -3\epsilon.\end{align*}
\begin{align*}X_t &= e^{-kt} \left(e^{ks} X_{s} + \int_{s}^{t} e^{u(k-\frac{1}{2}) } {\rm d}B_u \right) \\[4pt]
&\geq e^{-kt} (-2e^{ks} \epsilon -\epsilon )\\[4pt]
&\geq -3\epsilon.\end{align*}
Doing similarly for ![]() $Y_t$, we conclude.
$Y_t$, we conclude.
4. Analysis of  ${\rm d }{\textit{\textbf{L}}}_{\textit{\textbf{t}}} = \frac{|{\textit{\textbf{L}}}_{\textit{\textbf{t}}}|^{\textit{\textbf{k}}}}{{\textit{\textbf{t}}}^{\boldsymbol{\gamma}}} {\rm d}{\textit{\textbf{t}}} + \frac{1}{{\textit{\textbf{t}}}^{\boldsymbol{\gamma}}} {\rm d} {\textit{\textbf{B}}}_{\textit{\textbf{t}}}$
${\rm d }{\textit{\textbf{L}}}_{\textit{\textbf{t}}} = \frac{|{\textit{\textbf{L}}}_{\textit{\textbf{t}}}|^{\textit{\textbf{k}}}}{{\textit{\textbf{t}}}^{\boldsymbol{\gamma}}} {\rm d}{\textit{\textbf{t}}} + \frac{1}{{\textit{\textbf{t}}}^{\boldsymbol{\gamma}}} {\rm d} {\textit{\textbf{B}}}_{\textit{\textbf{t}}}$
4.1. Introduction
As in the previous section, to simplify matters, we will work with reparametrizing ![]() $L_t$. Set
$L_t$. Set ![]() $\theta (t) = t^{ \frac{1}{1-\gamma} }$, and let
$\theta (t) = t^{ \frac{1}{1-\gamma} }$, and let ![]() $ X_t= L_{ \theta (t)}$. To obtain the SDE that
$ X_t= L_{ \theta (t)}$. To obtain the SDE that ![]() $X_t$ obeys, notice that
$X_t$ obeys, notice that ![]() $ {\rm d} B_{ \theta (t) } = \sqrt{\theta ' (t)} {\rm d} B_t $. Therefore
$ {\rm d} B_{ \theta (t) } = \sqrt{\theta ' (t)} {\rm d} B_t $. Therefore
 \begin{align*}{ \rm d }X_t &= \frac{|X_t|^k}{\theta(t)^{\gamma}} \theta'(t){ \rm d}t + \frac{1}{\theta(t)^\gamma} \sqrt{\theta ' (t)}{\rm d} B_t \\&= c_1|X_t|^k { \rm d}t + c_2t^{-\frac{\gamma}{1-\gamma}} \sqrt{\theta ' (t)}{\rm d} B_t \\&=c_1|X_t|^k { \rm d}t + c_2t^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_t,\end{align*}
\begin{align*}{ \rm d }X_t &= \frac{|X_t|^k}{\theta(t)^{\gamma}} \theta'(t){ \rm d}t + \frac{1}{\theta(t)^\gamma} \sqrt{\theta ' (t)}{\rm d} B_t \\&= c_1|X_t|^k { \rm d}t + c_2t^{-\frac{\gamma}{1-\gamma}} \sqrt{\theta ' (t)}{\rm d} B_t \\&=c_1|X_t|^k { \rm d}t + c_2t^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_t,\end{align*}
where ![]() $c_2^2=c_1= 1/(1-\gamma)$. By abusing the notation we set
$c_2^2=c_1= 1/(1-\gamma)$. By abusing the notation we set ![]() $ X_t = X_t/c_2$, which satisfies an SDE of the form
$ X_t = X_t/c_2$, which satisfies an SDE of the form
where ![]() $k>1$,
$k>1$, ![]() $\gamma\in(1/2,1)$, and
$\gamma\in(1/2,1)$, and ![]() $c\in(0,\infty)$. By a time scaling, we may assume that
$c\in(0,\infty)$. By a time scaling, we may assume that ![]() $X_t$ solves
$X_t$ solves
where ![]() $k>1$ and
$k>1$ and ![]() $\gamma\in(1/2,1)$. Notice that the noise is scaled differently. However, it will be evident that only the order of the noise is relevant. The SDE (13) will be the primary focus of the next subsection, and the results will apply to solutions of (12) as well.
$\gamma\in(1/2,1)$. Notice that the noise is scaled differently. However, it will be evident that only the order of the noise is relevant. The SDE (13) will be the primary focus of the next subsection, and the results will apply to solutions of (12) as well.
We define another process that will be fundamental for our analysis, namely ![]() $\smash{Z_t=-\frac{X_t}{h(t)}}$, where
$\smash{Z_t=-\frac{X_t}{h(t)}}$, where ![]() $h(t)= -t^{\frac{1}{1-k}} $. Next, we find the SDE that
$h(t)= -t^{\frac{1}{1-k}} $. Next, we find the SDE that ![]() $Z_t$ satisfies.
$Z_t$ satisfies.
Proposition 4.1. Suppose that ![]() $(X_t)_{t\geq 1}$ solve (12), and set
$(X_t)_{t\geq 1}$ solve (12), and set ![]() $C(c)=\frac{1}{c(k-1)}$,
$C(c)=\frac{1}{c(k-1)}$, ![]() $h(t)= -t^{\frac{1}{1-k}} $. Then the process
$h(t)= -t^{\frac{1}{1-k}} $. Then the process ![]() $Z_t= -\frac{X_t}{h(t)}$ satisfies
$Z_t= -\frac{X_t}{h(t)}$ satisfies
Also, before ![]() $X_t$ hits zero we get a solution purely in terms of
$X_t$ hits zero we get a solution purely in terms of ![]() $Z_t$:
$Z_t$:
Proof. Recall that since h(t) is a continuous function, the covariance ![]() $ \langle h(t) , Z_t \rangle$ is 0. Using Itô’s formula we obtain
$ \langle h(t) , Z_t \rangle$ is 0. Using Itô’s formula we obtain
Thus,
 \begin{align*}Z_t - Z_s &= \int_{ s }^{t} -\frac{1}{h(u)} c|X_u| ^ k { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u + \int_{ s }^{t} X_u\frac{h'(u)}{ h(u) ^2} {\rm d }u \\[8pt]
&= \int_{ s }^{t} X_u\frac{h'(u)}{ h(u) ^2} -\frac{1}{h(u)} c|X_u| ^ k { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u \\[8pt]
&=\int_{ s }^{t}c\dfrac{X_u}{h(u) } \left(\frac{h'(u)}{c h(u) } - \frac{|X_u| ^k }{X_u}\right) { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u \\[8pt]
&=\int_{ s }^{t}c\dfrac{X_u}{h(u) } \left( \frac{1}{c(k-1)}\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u.\end{align*}
\begin{align*}Z_t - Z_s &= \int_{ s }^{t} -\frac{1}{h(u)} c|X_u| ^ k { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u + \int_{ s }^{t} X_u\frac{h'(u)}{ h(u) ^2} {\rm d }u \\[8pt]
&= \int_{ s }^{t} X_u\frac{h'(u)}{ h(u) ^2} -\frac{1}{h(u)} c|X_u| ^ k { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u \\[8pt]
&=\int_{ s }^{t}c\dfrac{X_u}{h(u) } \left(\frac{h'(u)}{c h(u) } - \frac{|X_u| ^k }{X_u}\right) { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u \\[8pt]
&=\int_{ s }^{t}c\dfrac{X_u}{h(u) } \left( \frac{1}{c(k-1)}\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u + \int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u.\end{align*}
The SDE (15) is an immediate consequence of the last line of the above calculation.
In the next proposition, we describe some properties of the noise for the process ![]() $Z_t$, and we give a very important inequality for Subsection 4.2, which relates the order of the deterministic system converging to zero and the order of the remaining noise for
$Z_t$, and we give a very important inequality for Subsection 4.2, which relates the order of the deterministic system converging to zero and the order of the remaining noise for ![]() $X_t$, i.e. the order of
$X_t$, i.e. the order of ![]() $\left \langle \int_s^\infty u^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_u\right \rangle$.
$\left \langle \int_s^\infty u^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_u\right \rangle$.
Proposition 4.2. Set ![]() $G'_{s,t}=\int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u$, the noise term of (15) and (14).
$G'_{s,t}=\int_{ s }^{t} -\frac{1}{h(u)}u^{-\frac{\gamma}{2(1-\gamma)}} { \rm d }B_u$, the noise term of (15) and (14).
1. In the regime
 $\frac{1}{2}+\frac{k}{2} \geq \gamma$,
$\frac{1}{2}+\frac{k}{2} \geq \gamma$,  $\langle G'_{s,\infty} \rangle =\infty$.
$\langle G'_{s,\infty} \rangle =\infty$.2. In the regime
 $\frac{1}{2}+\frac{k}{2} < \gamma$,
$\frac{1}{2}+\frac{k}{2} < \gamma$,  $\langle G'_{s,\infty} \rangle <\infty$.
$\langle G'_{s,\infty} \rangle <\infty$.3. Also, given the same conditions as in Part 1 for the pair
 $(k,\gamma)$, the following inequality is true:
$(k,\gamma)$, the following inequality is true:
 \begin{equation*} \frac{1}{k-1} \geq \frac{2\gamma -1}{2(1-\gamma)} . \end{equation*}
\begin{equation*} \frac{1}{k-1} \geq \frac{2\gamma -1}{2(1-\gamma)} . \end{equation*}
Proof. We calculate its quadratic variation at time t, namely,
Notice that by the definition of h(t), we have ![]() $h(t)^{-1} = \Theta \left(t^{\frac{1}{k-1}}\right)$; therefore
$h(t)^{-1} = \Theta \left(t^{\frac{1}{k-1}}\right)$; therefore
Consequently, ![]() $ \langle {G'}_{s,\infty}\rangle=\infty$ when
$ \langle {G'}_{s,\infty}\rangle=\infty$ when
In the first regime we have
 \begin{align}\frac{1}{2} +\frac{1}{2k} \geq \gamma &\iff \frac{k-1}{2k} \leq 1-\gamma \iff \frac{2k}{k-1} \geq \frac{1}{1-\gamma} \nonumber\\&\iff \frac{2}{k-1}+2 \geq \frac{1}{1-\gamma} \iff\frac{2}{k-1}+\frac{1}{1-\gamma} \geq -2. \end{align}
\begin{align}\frac{1}{2} +\frac{1}{2k} \geq \gamma &\iff \frac{k-1}{2k} \leq 1-\gamma \iff \frac{2k}{k-1} \geq \frac{1}{1-\gamma} \nonumber\\&\iff \frac{2}{k-1}+2 \geq \frac{1}{1-\gamma} \iff\frac{2}{k-1}+\frac{1}{1-\gamma} \geq -2. \end{align}
So, indeed, when ![]() $\frac{1}{2} +\frac{1}{2k}\geq \gamma$,
$\frac{1}{2} +\frac{1}{2k}\geq \gamma$, ![]() $\langle{G'}_{s,\infty}\rangle =\infty.$ Also, from the previous calculation we see that when
$\langle{G'}_{s,\infty}\rangle =\infty.$ Also, from the previous calculation we see that when ![]() $\frac{1}{2} +\frac{1}{2k}<\gamma$,
$\frac{1}{2} +\frac{1}{2k}<\gamma$,
therefore when ![]() $\frac{1}{2} +\frac{1}{2k}<\gamma$,
$\frac{1}{2} +\frac{1}{2k}<\gamma$, ![]() $\langle{G'}_{s,t}\rangle <\infty$. Finally, rearranging the first inequality of (16), we obtain
$\langle{G'}_{s,t}\rangle <\infty$. Finally, rearranging the first inequality of (16), we obtain
The solution of the SDE (13), when ![]() $X_t$ is positive, explodes in finite time. However, since we are interested in the behavior of
$X_t$ is positive, explodes in finite time. However, since we are interested in the behavior of ![]() $X_t$ when
$X_t$ when ![]() $X_t<M$ for a positive constant M, we may change the drift when
$X_t<M$ for a positive constant M, we may change the drift when ![]() $X_t$ surpasses the value M, which in turn would imply that the SDE (13) admits strong solutions. One way to do this is by studying the SDE whose drift term is equal to
$X_t$ surpasses the value M, which in turn would imply that the SDE (13) admits strong solutions. One way to do this is by studying the SDE whose drift term is equal to ![]() $|x|^k$ when
$|x|^k$ when ![]() $x<M$ and
$x<M$ and ![]() $M^k$ when
$M^k$ when ![]() $x>M$. This SDE can be seen to admit strong solutions for infinite time. The reason is that this process is a.s. bounded from below, and the drift is positive. Also,
$x>M$. This SDE can be seen to admit strong solutions for infinite time. The reason is that this process is a.s. bounded from below, and the drift is positive. Also, ![]() $X_t$ cannot explode to plus infinity in finite time since the drift is bounded from above when
$X_t$ cannot explode to plus infinity in finite time since the drift is bounded from above when ![]() $X_t$ is positive. However, for simplicity, we will use the form shown in (13).
$X_t$ is positive. However, for simplicity, we will use the form shown in (13).
4.2. Analysis of  ${\textit{\textbf{X}}}_{\textit{\textbf{t}}}$ when
${\textit{\textbf{X}}}_{\textit{\textbf{t}}}$ when  $\frac12 + \frac{1}{2{\textit{\textbf{k}}}} \geq \gamma$,
$\frac12 + \frac{1}{2{\textit{\textbf{k}}}} \geq \gamma$,  ${\textit{\textbf{k}}} > 1$, and
${\textit{\textbf{k}}} > 1$, and  $\gamma \in (\frac12,1)$
$\gamma \in (\frac12,1)$
The main result of this section is the following theorem.
Theorem 4.1. Let ![]() $(X_t)_{t\geq 1}$ solve (13). When
$(X_t)_{t\geq 1}$ solve (13). When ![]() $1/2 + 1/2k \geq \gamma$,
$1/2 + 1/2k \geq \gamma$, ![]() $X_t\rightarrow \infty$ a.s.
$X_t\rightarrow \infty$ a.s.
We will see its proof at the end of this subsection. Now we will prove an important proposition which shows that ![]() $X_t$ cannot stay far away from the left of the origin.
$X_t$ cannot stay far away from the left of the origin.
Proposition 4.3. Let ![]() $(X_t)_{t\geq 1}$ solve (12) for
$(X_t)_{t\geq 1}$ solve (12) for ![]() $c=1$. Then, for some
$c=1$. Then, for some ![]() $\beta<0$, the event
$\beta<0$, the event ![]() $\{X_t \geq \beta t^{\frac{1-2\gamma}{2(1-\gamma)} } \text{\ i.o.} \} $ has probability 1.
$\{X_t \geq \beta t^{\frac{1-2\gamma}{2(1-\gamma)} } \text{\ i.o.} \} $ has probability 1.
Proof. Set
which corresponds to the noise term of (15). First we will prove that ![]() $ \{ X_t \geq C' h(t) \text{\ i.o.} \}$ a.s., where
$ \{ X_t \geq C' h(t) \text{\ i.o.} \}$ a.s., where ![]() $C'> C^{\frac{1}{k-1}}$ and
$C'> C^{\frac{1}{k-1}}$ and ![]() $C=C(1)=\frac{1}{k-1}$. To do so, we will argue by contradiction. Assume that
$C=C(1)=\frac{1}{k-1}$. To do so, we will argue by contradiction. Assume that ![]() $A=\{ \exists\,s, X_t<C'\cdot h(t) \forall t>s \}$ has positive measure. Take
$A=\{ \exists\,s, X_t<C'\cdot h(t) \forall t>s \}$ has positive measure. Take ![]() $\omega \in A$, and find
$\omega \in A$, and find ![]() $s(\omega)$ such that
$s(\omega)$ such that ![]() $ X_t<C'\cdot h(t)$ for all
$ X_t<C'\cdot h(t)$ for all ![]() $t>s$. Notice that this implies that
$t>s$. Notice that this implies that ![]() $Z_t <-C'$ for
$Z_t <-C'$ for ![]() $t>s$. Take
$t>s$. Take ![]() $u>s$; since
$u>s$; since ![]() $ \frac{|x|^k}{x}$ is increasing we see that
$ \frac{|x|^k}{x}$ is increasing we see that
This in turn gives
Therefore
for all ![]() $t>0$. However, since the process
$t>0$. However, since the process
for any fixed w has infinite quadratic variation, we may find ![]() $G'_{s,t} >-Z_s$. Now, from (14) we get
$G'_{s,t} >-Z_s$. Now, from (14) we get
 \begin{align*}Z_t &= \int_{ s }^{t}\dfrac{X_u}{h(u) } \left(C\frac{ |h(u)|^k }{h(u )} -\frac{ |X_u|^k }{X_u}\right) { \rm d } u + Z_s +G'_{s,t}\\&>0.\end{align*}
\begin{align*}Z_t &= \int_{ s }^{t}\dfrac{X_u}{h(u) } \left(C\frac{ |h(u)|^k }{h(u )} -\frac{ |X_u|^k }{X_u}\right) { \rm d } u + Z_s +G'_{s,t}\\&>0.\end{align*}
This contradicts the fact that ![]() $Z_t<-C'$. Therefore
$Z_t<-C'$. Therefore ![]() $ \{X_t> C'h(t) \text{\ i.o.} \}$ a.s.
$ \{X_t> C'h(t) \text{\ i.o.} \}$ a.s.
Finally, in Proposition 4.2 Part 3 we have shown that ![]() $\frac{1}{k-1}\geq \frac{2\gamma -1}{2(1-\gamma )} $; therefore
$\frac{1}{k-1}\geq \frac{2\gamma -1}{2(1-\gamma )} $; therefore
So we conclude that there exists a constant ![]() $\beta<0$ such that
$\beta<0$ such that ![]() $\{ X_t \geq \beta t^{ \frac{1-2\gamma}{ 2(1-\gamma)}}\ \text{\,i.o.} \} $ holds a.s.
$\{ X_t \geq \beta t^{ \frac{1-2\gamma}{ 2(1-\gamma)}}\ \text{\,i.o.} \} $ holds a.s.
Corollary 4.1. Let ![]() $(X_t)_{t\geq 1}$ solve (12) for
$(X_t)_{t\geq 1}$ solve (12) for ![]() $c=1$. Then
$c=1$. Then ![]() $\liminf_{t \rightarrow \infty } X_t>0$ a.s.
$\liminf_{t \rightarrow \infty } X_t>0$ a.s.
Proof. Set ![]() $G_{s,t}=\int_s^t u^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_u $, and note that
$G_{s,t}=\int_s^t u^{-\frac{\gamma}{2(1-\gamma)}} {\rm d} B_u $, and note that ![]() $ \langle G_{s,\infty}\rangle = \Theta (s^{ \frac{1-2\gamma}{ (1-\gamma)} } )$. Fix
$ \langle G_{s,\infty}\rangle = \Theta (s^{ \frac{1-2\gamma}{ (1-\gamma)} } )$. Fix ![]() $\gamma>0$; since
$\gamma>0$; since ![]() $ \langle G_{s,\infty}\rangle = \Theta (s^{ \frac{1-2\gamma}{ (1-\gamma)} } )$ for any
$ \langle G_{s,\infty}\rangle = \Theta (s^{ \frac{1-2\gamma}{ (1-\gamma)} } )$ for any ![]() $u>0$, it is possible to find
$u>0$, it is possible to find ![]() $W(u)>u>0$ such that
$W(u)>u>0$ such that
 \begin{equation}{}\mathbb{P}\left(\sup_{u<t<W(u)}G_{u,t} > \gamma u^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)> \delta,\end{equation}
\begin{equation}{}\mathbb{P}\left(\sup_{u<t<W(u)}G_{u,t} > \gamma u^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)> \delta,\end{equation}
for ![]() $\delta$ independent of u. Take
$\delta$ independent of u. Take ![]() $\gamma>-\beta$, where
$\gamma>-\beta$, where ![]() $\beta$ is such that
$\beta$ is such that ![]() $\{X_t\geq \beta t^{\frac{1-2\gamma}{2(1-\gamma)}} \text{\ i.o.} \}$ (as in Proposition 4.3). Now, using the lower bound
$\{X_t\geq \beta t^{\frac{1-2\gamma}{2(1-\gamma)}} \text{\ i.o.} \}$ (as in Proposition 4.3). Now, using the lower bound ![]() $ X_t-X_s \geq G_{s,t}$, we obtain
$ X_t-X_s \geq G_{s,t}$, we obtain
 \begin{equation} \mathbb{P}\left(\sup_{s<t<W(s)}X_t-X_s > \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\geq \mathbb{P}\left(\sup_{s<t<W(s)}G_{s,t} > \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)> \delta. \end{equation}
\begin{equation} \mathbb{P}\left(\sup_{s<t<W(s)}X_t-X_s > \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\geq \mathbb{P}\left(\sup_{s<t<W(s)}G_{s,t} > \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)> \delta. \end{equation}
When ![]() $X_s\geq \beta s^{\frac{1-2\gamma}{2(1-\gamma)}}$, observe that on the event
$X_s\geq \beta s^{\frac{1-2\gamma}{2(1-\gamma)}}$, observe that on the event
 \begin{equation*}\Bigg\{ \sup_{s<t<W(s)}X_t-X_s> \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \Bigg\}\end{equation*}
\begin{equation*}\Bigg\{ \sup_{s<t<W(s)}X_t-X_s> \gamma s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \Bigg\}\end{equation*}
there is ![]() $\tau_s$ such that
$\tau_s$ such that
Hence, if we choose a sequence of stopping times such that ![]() $X_{\tau_n}\geq \beta {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$ and
$X_{\tau_n}\geq \beta {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$ and ![]() $\tau_{ n+1}> W(\tau_n)$, we have
$\tau_{ n+1}> W(\tau_n)$, we have
So, by Borel–Cantelli (Lemma 2.5), on the events
 \begin{equation*}\Bigg\{\sup_{\tau_n<t<\tau_{ n+1}}X_t-X_{\tau_n} > \gamma \tau_n^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \Bigg\}\end{equation*}
\begin{equation*}\Bigg\{\sup_{\tau_n<t<\tau_{ n+1}}X_t-X_{\tau_n} > \gamma \tau_n^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \Bigg\}\end{equation*}
we may conclude that ![]() $\{X_t\geq 0 \text{\ i.o.}\}$ has probability 1. Define
$\{X_t\geq 0 \text{\ i.o.}\}$ has probability 1. Define ![]() $\tau_n$ as before, except that instead of
$\tau_n$ as before, except that instead of ![]() $X_{\tau_n}\geq \beta {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$ we set
$X_{\tau_n}\geq \beta {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$ we set ![]() $X_{\tau_n}\geq 0$; by Borel–Cantelli we obtain that
$X_{\tau_n}\geq 0$; by Borel–Cantelli we obtain that ![]() $\{X_t\geq \gamma t^{\frac{1-2\gamma}{2(1-\gamma)}} \text{\ i.o.}\}$ has probability 1.
$\{X_t\geq \gamma t^{\frac{1-2\gamma}{2(1-\gamma)}} \text{\ i.o.}\}$ has probability 1.
Since ![]() $G_{s,t}$ is symmetric and
$G_{s,t}$ is symmetric and ![]() $\langle G_{s,\infty}\rangle = \Theta \left(s^{ \frac{1-2\gamma}{ 1-\gamma} } \right)$, we have
$\langle G_{s,\infty}\rangle = \Theta \left(s^{ \frac{1-2\gamma}{ 1-\gamma} } \right)$, we have
 \begin{align*}\mathbb{P}\left(\inf_{s<t<\infty }X_t-X_s > -\frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)&\geq \mathbb{P}\left(\inf_{s<t<\infty}G_{s,t} > -\frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\\[5pt]
&=1-\mathbb{P}\left(\sup_{s<t<\infty}G_{s,t} > \frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\\&>\delta'>0.\end{align*}
\begin{align*}\mathbb{P}\left(\inf_{s<t<\infty }X_t-X_s > -\frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)&\geq \mathbb{P}\left(\inf_{s<t<\infty}G_{s,t} > -\frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\\[5pt]
&=1-\mathbb{P}\left(\sup_{s<t<\infty}G_{s,t} > \frac{\gamma}{2} s^{ \frac{1-2\gamma}{ 2(1-\gamma)} } \right)\\&>\delta'>0.\end{align*}
for some ![]() $\delta'$ independent of s.
$\delta'$ independent of s.
Define ![]() $\tau_n$ such that
$\tau_n$ such that ![]() $X_{\tau_n}\geq \gamma {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$, and set
$X_{\tau_n}\geq \gamma {\tau_n}^{\frac{1-2\gamma}{2(1-\gamma)}}$, and set ![]() $\mathcal{F}_{\tau_n}=\mathcal{F}_n$. To show that
$\mathcal{F}_{\tau_n}=\mathcal{F}_n$. To show that ![]() $A=\{\liminf_{\rightarrow \infty} X_t\leq 0\}$ has probability zero, it suffices to argue that there is a
$A=\{\liminf_{\rightarrow \infty} X_t\leq 0\}$ has probability zero, it suffices to argue that there is a ![]() $\delta$ such that
$\delta$ such that ![]() $ \mathbb{P}( A|\mathcal{F}_n )<1-\delta $ a.s. for all
$ \mathbb{P}( A|\mathcal{F}_n )<1-\delta $ a.s. for all ![]() $n\geq 1$. This is immediate from the previous calculation. Indeed,
$n\geq 1$. This is immediate from the previous calculation. Indeed,
 \begin{align*}\mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P} \left(\inf_{ \tau_{n}\leq u <\infty } X_u -X_{\tau_n}>-\frac{\gamma}{2} {\tau_n}^{ \frac{1-2\gamma}{ 2(1-\gamma)} } |\mathcal{F}_n \right)\\&<1-\delta'.\end{align*}
\begin{align*}\mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P} \left(\inf_{ \tau_{n}\leq u <\infty } X_u -X_{\tau_n}>-\frac{\gamma}{2} {\tau_n}^{ \frac{1-2\gamma}{ 2(1-\gamma)} } |\mathcal{F}_n \right)\\&<1-\delta'.\end{align*}
Proof of Theorem 4.1. Since ![]() $X_t$ is a solution of (13), we have
$X_t$ is a solution of (13), we have ![]() $X_t-X_1=\int_{1}^t |X_u|^k \text{d}u+G_{1,t} $. From Corollary 4.1 we know that
$X_t-X_1=\int_{1}^t |X_u|^k \text{d}u+G_{1,t} $. From Corollary 4.1 we know that ![]() $\liminf_{t \rightarrow \infty}X_t>0$ a.s.; therefore
$\liminf_{t \rightarrow \infty}X_t>0$ a.s.; therefore ![]() $\int_{1}^t |X_u|^k \text{d}u \rightarrow \infty$ a.s. However, since
$\int_{1}^t |X_u|^k \text{d}u \rightarrow \infty$ a.s. However, since ![]() $\langle G_{1,\infty}\rangle<\infty$, we have that
$\langle G_{1,\infty}\rangle<\infty$, we have that ![]() $\limsup_{t \rightarrow \infty }|G_{1,t}|<\infty$ a.s. Therefore,
$\limsup_{t \rightarrow \infty }|G_{1,t}|<\infty$ a.s. Therefore, ![]() $X_t \rightarrow \infty$ a.s.
$X_t \rightarrow \infty$ a.s.
4.3 Analysis of  ${\textit{\textbf{X}}}_{\textit{\textbf{t}}}$ when
${\textit{\textbf{X}}}_{\textit{\textbf{t}}}$ when  $\frac{1}{2} + \frac{1}{2{\textit{\textbf{k}}}} < \gamma $ and
$\frac{1}{2} + \frac{1}{2{\textit{\textbf{k}}}} < \gamma $ and  ${\textit{\textbf{k}}} > 1$
${\textit{\textbf{k}}} > 1$
We now state the main theorem of this section, which we will prove at the end.
Theorem 4.2. The process ![]() $(X_t)_{t\geq 1}$, the solution of (12), converges to zero with positive probability, when
$(X_t)_{t\geq 1}$, the solution of (12), converges to zero with positive probability, when ![]() $X_1<0$.
$X_1<0$.
We prove a technical lemma first.
Lemma 4.1. Let ![]() $(Z_t)_{t\geq s}$ solve (14), and set
$(Z_t)_{t\geq s}$ solve (14), and set
Suppose that ![]() $Z_s>-\left(\frac{C}{k} \right)^{\frac{1}{k-1}}$. Define
$Z_s>-\left(\frac{C}{k} \right)^{\frac{1}{k-1}}$. Define
Then the following hold:
1.
 $\mathbb{P}( A) >0$ for every
$\mathbb{P}( A) >0$ for every  $\epsilon,\delta >0$.
$\epsilon,\delta >0$.2. For all
 $\epsilon>0$ small enough, there is
$\epsilon>0$ small enough, there is  $\delta>0$ such that
$\delta>0$ such that  $Z_t<-\dfrac{5\epsilon}{3}$ for every
$Z_t<-\dfrac{5\epsilon}{3}$ for every  $t \in (s, s+\delta)$ on A.
$t \in (s, s+\delta)$ on A.3. Define
 $\tau_C = \inf \Big\{t>s| Z_t= - 2 \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \Big\}$. Then
$\tau_C = \inf \Big\{t>s| Z_t= - 2 \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \Big\}$. Then  $\tau_C>s+\delta$ a.s., where
$\tau_C>s+\delta$ a.s., where  $\delta$ is the same as in Part 2.
$\delta$ is the same as in Part 2.
Proof.
-
1. This is immediate, since in Proposition 4.2 Part 2 we have shown that
 $\langle G'_{\infty} \rangle <\infty$.
$\langle G'_{\infty} \rangle <\infty$. -
2. The first restriction on
 $\epsilon$ is such that
$\epsilon$ is such that  $Z_s<-3\epsilon$. Next, we begin by defining
$Z_s<-3\epsilon$. Next, we begin by defining  $f_1$ and
$f_1$ and  $f_2$ on
$f_2$ on  $(s, s+\delta)$ satisfying
(20)where c and C are the same as the parameters of the SDE (14), with initial conditions satisfying
$(s, s+\delta)$ satisfying
(20)where c and C are the same as the parameters of the SDE (14), with initial conditions satisfying \begin{equation} f'(x) = c|h(x)|^{k-1} f(x) (C-(-f(x)^{k-1}) ), \end{equation}
and
\begin{equation} f'(x) = c|h(x)|^{k-1} f(x) (C-(-f(x)^{k-1}) ), \end{equation}
and \begin{equation*} -\left(\frac{C}{k} \right)^{\frac{1}{k-1}} < Z_s +\epsilon< f_1(s ) <-\dfrac{5\epsilon}{3} \end{equation*}
Also, we define the function
\begin{equation*} -\left(\frac{C}{k} \right)^{\frac{1}{k-1}} < Z_s +\epsilon< f_1(s ) <-\dfrac{5\epsilon}{3} \end{equation*}
Also, we define the function \begin{equation*} -\left(\frac{C}{k} \right)^{\frac{1}{k-1}}<f_2(s )
< Z_s-\epsilon .\qquad\quad\end{equation*}
\begin{equation*} -\left(\frac{C}{k} \right)^{\frac{1}{k-1}}<f_2(s )
< Z_s-\epsilon .\qquad\quad\end{equation*}
 $ q(x) = x(C- (-x)^{k-1} ) $, whose derivative is
$ q(x) = x(C- (-x)^{k-1} ) $, whose derivative is  $ q'(x) = C-k(-x)^{k-1}$, which implies that q(x) is increasing on
$ q'(x) = C-k(-x)^{k-1}$, which implies that q(x) is increasing on  $ \big( \big(-\frac{C}{k} \big)^{\frac{1}{k-1}} ,0 \big) $. This function will be important later. We should also note that f is decreasing in intervals where
$ \big( \big(-\frac{C}{k} \big)^{\frac{1}{k-1}} ,0 \big) $. This function will be important later. We should also note that f is decreasing in intervals where  $f(x) \in \big( - \big(\frac{C}{k} \big)^{\frac{1}{k-1}} ,0 \big)$, since there
$f(x) \in \big( - \big(\frac{C}{k} \big)^{\frac{1}{k-1}} ,0 \big)$, since there  $f'(x)<0$.
$f'(x)<0$.
We can pick the
 $\delta>0$ so that
$\delta>0$ so that  $f_2(t)>- \big(\frac{C}{k} \big)^{\frac{1}{k-1}}$ for every
$f_2(t)>- \big(\frac{C}{k} \big)^{\frac{1}{k-1}}$ for every  $t \in ( s, s+\delta ) $. We will show that
$t \in ( s, s+\delta ) $. We will show that  $ Z_t>f_2(t)$ on
$ Z_t>f_2(t)$ on  $( s, s+\delta ) $ by contradiction. Using the SDE (15) for
$( s, s+\delta ) $ by contradiction. Using the SDE (15) for  $Z_t$, we get that
(21)where g(t) is a continuous function such that
$Z_t$, we get that
(21)where g(t) is a continuous function such that \begin{equation} Z_t- Z_s = \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left( C- (-Z_u )^ {k-1}\right) { \rm d } u + g(t), \end{equation}
\begin{equation} Z_t- Z_s = \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left( C- (-Z_u )^ {k-1}\right) { \rm d } u + g(t), \end{equation}
 $ \sup_{t\in ( s, s+\delta ) } |g(t)| \leq \epsilon. $ Assume that
$ \sup_{t\in ( s, s+\delta ) } |g(t)| \leq \epsilon. $ Assume that  $f_2$ and Z become equal at some point, and choose t to be the first time. Using the integral form of (20), and subtracting it from (15), we get
where in the last line we used that
$f_2$ and Z become equal at some point, and choose t to be the first time. Using the integral form of (20), and subtracting it from (15), we get
where in the last line we used that \begin{align*} 0&=Z_t- f_2(t) \\[2pt]&= \int_{ s }^{t} c|h(u)|^{k-1} Z_u \big(C- (-Z_u )^ {k-1}\big) -c|h(u)|^{k-1} f_2(u) \big(C- (-f_2(u)) ^ {k-1}\big) { \rm d } u \\[2pt]&\quad +Z_s- f_2(s)+ g(t) \\[2pt] &= (t-s)\big(c|h(\xi)|^{k-1} Z_{\xi} \big(C- ( -Z_{\xi}) ^ {k-1}\big) -c|h(\xi)|^{k-1} f_2(\xi) \big(C- (-f_2(\xi)) ^ {k-1}\big) \big) \\[2pt] &\quad +Z_s+g(t) - f_2(s)\\[2pt] &>(t-s)\big(c|h(\xi)|^{k-1} Z_{\xi} \big(C- (-Z_{\xi}) ^ {k-1}\big)-c|h(\xi)|^{k-1} f_2(\xi) \big(C- (-f_2(\xi)) ^ {k-1}\big)\big), \end{align*}
\begin{align*} 0&=Z_t- f_2(t) \\[2pt]&= \int_{ s }^{t} c|h(u)|^{k-1} Z_u \big(C- (-Z_u )^ {k-1}\big) -c|h(u)|^{k-1} f_2(u) \big(C- (-f_2(u)) ^ {k-1}\big) { \rm d } u \\[2pt]&\quad +Z_s- f_2(s)+ g(t) \\[2pt] &= (t-s)\big(c|h(\xi)|^{k-1} Z_{\xi} \big(C- ( -Z_{\xi}) ^ {k-1}\big) -c|h(\xi)|^{k-1} f_2(\xi) \big(C- (-f_2(\xi)) ^ {k-1}\big) \big) \\[2pt] &\quad +Z_s+g(t) - f_2(s)\\[2pt] &>(t-s)\big(c|h(\xi)|^{k-1} Z_{\xi} \big(C- (-Z_{\xi}) ^ {k-1}\big)-c|h(\xi)|^{k-1} f_2(\xi) \big(C- (-f_2(\xi)) ^ {k-1}\big)\big), \end{align*}
 $Z_s+g(t) - f_2(s)> 0$. Since
$Z_s+g(t) - f_2(s)> 0$. Since  $\xi <t$, we have that
$\xi <t$, we have that  $ Z_{\xi}>f_2(\xi) > -\left(\frac{C}{k} \right)^{\frac{1}{k-1}} $, and consequently
$ Z_{\xi}>f_2(\xi) > -\left(\frac{C}{k} \right)^{\frac{1}{k-1}} $, and consequently  $ q(Z_{\xi} ) > q( f_2(\xi) ) $, so
Therefore,
$ q(Z_{\xi} ) > q( f_2(\xi) ) $, so
Therefore, \begin{equation*} |h(\xi)|^{k-1} q(Z_{\xi} ) > |h(\xi)|^{k-1} q( f_2(\xi) ) .\end{equation*}
which gives a contradiction.
\begin{equation*} |h(\xi)|^{k-1} q(Z_{\xi} ) > |h(\xi)|^{k-1} q( f_2(\xi) ) .\end{equation*}
which gives a contradiction. \begin{equation*}0
< c|h(\xi)|^{k-1} Z_{\xi} \left(C- (-Z_{\xi}) ^ {k-1}\right) -c|h(\xi)|^{k-1} f_2(\xi) \left(C- (-f_2(\xi)) ^ {k-1}\right), \end{equation*}
\begin{equation*}0
< c|h(\xi)|^{k-1} Z_{\xi} \left(C- (-Z_{\xi}) ^ {k-1}\right) -c|h(\xi)|^{k-1} f_2(\xi) \left(C- (-f_2(\xi)) ^ {k-1}\right), \end{equation*}
Arguing similarly we can show that
 $ f_1(t)> Z_t$ on
$ f_1(t)> Z_t$ on  $ (s, s+\delta)$, which completes Part 2.
$ (s, s+\delta)$, which completes Part 2. -
3. Finally, for Part 3 we observe that
 $Z_t>f_2(t)$ for
$Z_t>f_2(t)$ for  $t\in (s,s+\delta)$; hence
$t\in (s,s+\delta)$; hence  $\tau_C >s+\delta$ a.s.
$\tau_C >s+\delta$ a.s.
Before proving the theorem we will need the following proposition.
Proposition 4.4. Let ![]() $(X_t)_{t\geq s}$ solve (12). Assume that at time s,
$(X_t)_{t\geq s}$ solve (12). Assume that at time s, ![]() $X_s<0$, and
$X_s<0$, and ![]() $Z_s>- \left(\frac{C}{k} \right)^{\frac{1}{k-1}}$. Then with positive probability the process never returns to 0.
$Z_s>- \left(\frac{C}{k} \right)^{\frac{1}{k-1}}$. Then with positive probability the process never returns to 0.
Proof. The condition ![]() $1/2 + 1/2k <\gamma$, as has already been shown in Section 4.2, implies that
$1/2 + 1/2k <\gamma$, as has already been shown in Section 4.2, implies that ![]() $ \langle G'_{\infty} \rangle <\infty$. On the event A as defined in Lemma 2.3, using (14), we get the following upper and lower bounds for all
$ \langle G'_{\infty} \rangle <\infty$. On the event A as defined in Lemma 2.3, using (14), we get the following upper and lower bounds for all ![]() $t\geq s+\delta$:
$t\geq s+\delta$:
Claim: On the event A, ![]() $X_t < 0$ for all
$X_t < 0$ for all ![]() $t>s$.
$t>s$.
Proof: We will argue by contradiction. Assume that ![]() $\mathbb{P}(\{ \tau_0 <\infty \}\cap A) >0$. We choose
$\mathbb{P}(\{ \tau_0 <\infty \}\cap A) >0$. We choose ![]() $\epsilon$ such that
$\epsilon$ such that ![]() $ \frac{3\epsilon}{2}<C^{\frac{1}{k-1} } $. Now, define
$ \frac{3\epsilon}{2}<C^{\frac{1}{k-1} } $. Now, define ![]() $\tau_{l} = \sup \{ t\leq \tau_0 |-\tfrac{X_t}{h(t) } = -\frac{3\epsilon}{2} \} $ and notice that Lemma 4.1 implies that
$\tau_{l} = \sup \{ t\leq \tau_0 |-\tfrac{X_t}{h(t) } = -\frac{3\epsilon}{2} \} $ and notice that Lemma 4.1 implies that ![]() $ \tau_{ l \epsilon }>s+\delta$, since
$ \tau_{ l \epsilon }>s+\delta$, since ![]() $Z_t< -\frac{5 \epsilon}{3}$ on
$Z_t< -\frac{5 \epsilon}{3}$ on ![]() $(s,s+\delta)$. Also, on
$(s,s+\delta)$. Also, on ![]() $\{ \tau_0 <\infty \}\cap A$ we have
$\{ \tau_0 <\infty \}\cap A$ we have ![]() $\tau_{ l}<\infty$. Then from (23) we see that
$\tau_{ l}<\infty$. Then from (23) we see that
Therefore,
Now, notice that ![]() $ X_t > \frac{3}{2} \epsilon h(t)$ for every
$ X_t > \frac{3}{2} \epsilon h(t)$ for every ![]() $t \in ( \tau_{l},\tau_0 )$, so if
$t \in ( \tau_{l},\tau_0 )$, so if ![]() $w \in ( \tau_{l},\tau_0 ),$ we get
$w \in ( \tau_{l},\tau_0 ),$ we get
and of course ![]() $ \frac{X_w}{ h(w)} >0$. So we conclude that
$ \frac{X_w}{ h(w)} >0$. So we conclude that
Combining (24) and (25), we get that
 \begin{align*}0 & =-\frac{X_{\tau_0}}{h(\tau_0)} \\[6pt]
& \leq-\frac{X_s}{h(s)} +\int_{ s }^{\tau_0}c\dfrac{X_u}{h(u) } \left(C \frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u -\frac{9}{10}\epsilon \\[6pt]
& = -\frac{X_s}{h(s)} +\int_{ s }^{\tau_l}c\dfrac{X_u}{h(u) } \left(C\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u -\frac{9}{10}\epsilon\\[6pt]
&\quad + \int_{ \tau_l }^{\tau_0}c\dfrac{X_u}{h(u) } \left(C\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u \\[6pt]
& \leq -\frac{2\epsilon}{5},\end{align*}
\begin{align*}0 & =-\frac{X_{\tau_0}}{h(\tau_0)} \\[6pt]
& \leq-\frac{X_s}{h(s)} +\int_{ s }^{\tau_0}c\dfrac{X_u}{h(u) } \left(C \frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u -\frac{9}{10}\epsilon \\[6pt]
& = -\frac{X_s}{h(s)} +\int_{ s }^{\tau_l}c\dfrac{X_u}{h(u) } \left(C\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u -\frac{9}{10}\epsilon\\[6pt]
&\quad + \int_{ \tau_l }^{\tau_0}c\dfrac{X_u}{h(u) } \left(C\frac{|h(u)|^k }{h(u)} -\frac{|X_u| ^k }{X_u}\right) { \rm d } u \\[6pt]
& \leq -\frac{2\epsilon}{5},\end{align*}
a contradiction.
We have developed all the tools necessary to prove the theorem.
Proof of Theorem 4.2. Define a stopping time ![]() $\sigma=\inf \{ t | Z_t>-\left(\frac{C}{k} \right)^{\frac{1}{k-1}} \}$. If the event
$\sigma=\inf \{ t | Z_t>-\left(\frac{C}{k} \right)^{\frac{1}{k-1}} \}$. If the event ![]() $\{\sigma<\infty\}$ has positive probability, then Proposition 4.4 implies that
$\{\sigma<\infty\}$ has positive probability, then Proposition 4.4 implies that ![]() $X_t$ converges to zero with positive probability. Indeed, recall from Lemma 1 that
$X_t$ converges to zero with positive probability. Indeed, recall from Lemma 1 that ![]() $\liminf_{t\rightarrow \infty}X_t \geq 0$ a.s. Therefore, since on the event A as in Lemma 4.1 we have
$\liminf_{t\rightarrow \infty}X_t \geq 0$ a.s. Therefore, since on the event A as in Lemma 4.1 we have ![]() $\limsup_{t \rightarrow \infty }X_t \leq 0$, we deduce that
$\limsup_{t \rightarrow \infty }X_t \leq 0$, we deduce that ![]() $\lim_{t\rightarrow \infty }X_t=0$. To finish the proof, it suffices to show that when
$\lim_{t\rightarrow \infty }X_t=0$. To finish the proof, it suffices to show that when ![]() $\{\sigma<\infty\}$ has zero probability,
$\{\sigma<\infty\}$ has zero probability, ![]() $X_t\rightarrow 0$ with positive probability. This is easy to see since
$X_t\rightarrow 0$ with positive probability. This is easy to see since ![]() $\mathbb{P}(\{\sigma<\infty\})=0$ implies that
$\mathbb{P}(\{\sigma<\infty\})=0$ implies that ![]() $Z_t$ never hits zero; therefore
$Z_t$ never hits zero; therefore ![]() $\limsup_{t \rightarrow \infty }X_t \leq 0$ on
$\limsup_{t \rightarrow \infty }X_t \leq 0$ on ![]() $\{\sigma<\infty \}$.
$\{\sigma<\infty \}$.
We now prove a proposition that will be used in the next section.
Proposition 4.5. Let ![]() $(X_t)_{t\geq s}$ solve (12). Take the event A such that Lemma 4.1 holds, with
$(X_t)_{t\geq s}$ solve (12). Take the event A such that Lemma 4.1 holds, with ![]() $\epsilon <\big(\frac{C}{k} \big) ^{\frac{1}{k-1}}$, where
$\epsilon <\big(\frac{C}{k} \big) ^{\frac{1}{k-1}}$, where ![]() $C(c)=\frac{1}{c(k-1)}$ as in the parameter C of the SDE (14). Then, on A, the process
$C(c)=\frac{1}{c(k-1)}$ as in the parameter C of the SDE (14). Then, on A, the process ![]() $X_t$ stays within a region of the origin. More specifically,
$X_t$ stays within a region of the origin. More specifically, ![]() $Z_t> -2\big(\frac{C}{k} \big) ^{\frac{1}{k-1}}$.
$Z_t> -2\big(\frac{C}{k} \big) ^{\frac{1}{k-1}}$.
Proof. Let ![]() $\tau_C = \inf \left\{t>s| Z_t= - 2 \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \right\}$, and define
$\tau_C = \inf \left\{t>s| Z_t= - 2 \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \right\}$, and define
 \begin{equation*}\sigma= \sup \left\{\tau_C >t>s|Z_t= - \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \right\}.\end{equation*}
\begin{equation*}\sigma= \sup \left\{\tau_C >t>s|Z_t= - \left(\frac{C}{k} \right) ^{\frac{1}{k-1}} \right\}.\end{equation*}
We will show that ![]() $\tau_C=\infty$ a.s. We assume otherwise, and reach a contradiction. From Lemma 4.1 Part 3, we know that
$\tau_C=\infty$ a.s. We assume otherwise, and reach a contradiction. From Lemma 4.1 Part 3, we know that ![]() $\tau_C>s+\delta$. Therefore,
$\tau_C>s+\delta$. Therefore,
 \begin{align*}Z_{ \tau_C} &\geq Z_s+ \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left(C- (-Z_u) ^ {k-1}\right) { \rm d } u -2\epsilon \\&\geq Z_{\sigma} -Z_{\sigma}+Z_s+ \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left(C- (-Z_u) ^ {k-1}\right) { \rm d } u -2\epsilon \\&\geq Z_{\sigma} +\frac{9\epsilon}{10} -2\epsilon >-2\left(\frac{C}{k} \right) ^{\frac{1}{k-1}},\end{align*}
\begin{align*}Z_{ \tau_C} &\geq Z_s+ \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left(C- (-Z_u) ^ {k-1}\right) { \rm d } u -2\epsilon \\&\geq Z_{\sigma} -Z_{\sigma}+Z_s+ \int_{ s }^{t}c|h(u)|^{k-1} Z_u \left(C- (-Z_u) ^ {k-1}\right) { \rm d } u -2\epsilon \\&\geq Z_{\sigma} +\frac{9\epsilon}{10} -2\epsilon >-2\left(\frac{C}{k} \right) ^{\frac{1}{k-1}},\end{align*}
the desired contradiction.
5. Analysis of  ${ \rm d }\textbf{\textit{L}}_{\textbf{\textit{t}}} = \frac{{\textbf{\textit{f}}}({\textbf{\textit{L}}}_{\textbf{\textit{t}}})}{{\textbf{\textit{t}}}^{\gamma}} { \rm d}{\textbf{\textit{t}}} + \frac{1}{{\textbf{\textit{t}}}^\gamma} {\rm d} {\textbf{\textit{B}}}_{\textbf{\textit{t}}} $
${ \rm d }\textbf{\textit{L}}_{\textbf{\textit{t}}} = \frac{{\textbf{\textit{f}}}({\textbf{\textit{L}}}_{\textbf{\textit{t}}})}{{\textbf{\textit{t}}}^{\gamma}} { \rm d}{\textbf{\textit{t}}} + \frac{1}{{\textbf{\textit{t}}}^\gamma} {\rm d} {\textbf{\textit{B}}}_{\textbf{\textit{t}}} $
For this section, we assume that f is globally Lipschitz. For f as before, we define
By our assumptions on f, the SDE (26) admits strong solutions. Also, we define a more general SDE, namely
where ![]() $g\,:\,\mathbb{R}_{\geq 0}\rightarrow \mathbb{R}_{>0}$ is continuous, and
$g\,:\,\mathbb{R}_{\geq 0}\rightarrow \mathbb{R}_{>0}$ is continuous, and ![]() $T=\int_{0}^\infty g^2(t)\text{d}t$ is possibly infinite.
$T=\int_{0}^\infty g^2(t)\text{d}t$ is possibly infinite.
Proposition 5.1. Let ![]() $(X_t)_{t\geq 1}$ be a solution of (27). Then for every
$(X_t)_{t\geq 1}$ be a solution of (27). Then for every ![]() $t,c>0$ and
$t,c>0$ and ![]() $x\in \mathbb{R}$,
$x\in \mathbb{R}$, ![]() $\mathbb{P}( X_t \in(x-c ,x+c ) )>0$.
$\mathbb{P}( X_t \in(x-c ,x+c ) )>0$.
Proof. Firstly, we change time. Let ![]() $\xi(t)= \int_{0}^{t} g^2(t)\text{d}t $, and define
$\xi(t)= \int_{0}^{t} g^2(t)\text{d}t $, and define ![]() $\tilde{X}_t =X_{\xi^{-1}(t)}$. Then
$\tilde{X}_t =X_{\xi^{-1}(t)}$. Then
This gives a well-defined SDE whose solution is defined on [0,T] for ![]() $T'\in \mathbb{R},$
$T'\in \mathbb{R},$ ![]() $\xi(t)<T'<T$. The path-space measure of
$\xi(t)<T'<T$. The path-space measure of ![]() $\tilde{X}_t$ is mutually absolutely continuous to the one induced from the Brownian motion. Since the Brownian motion satisfies the property described in the proposition, so does
$\tilde{X}_t$ is mutually absolutely continuous to the one induced from the Brownian motion. Since the Brownian motion satisfies the property described in the proposition, so does ![]() $X_t$.
$X_t$.
We give the proofs of Theorems 1.2 and 1.3. For the proofs, we use that the theorems hold if and only if they hold for their corresponding reparametrizations.
Proof of Theorem 1.2 Parts 1 & 2. Both parts can be proved simultaneously. Let ![]() $\tau = \inf \{ t|X_t \in ( -\epsilon,\epsilon ) \} $ and
$\tau = \inf \{ t|X_t \in ( -\epsilon,\epsilon ) \} $ and ![]() $\tau' =\inf\{t>\tau| X_t \in \{-3\epsilon,3\epsilon\} \}$. Now, define a stochastic process
$\tau' =\inf\{t>\tau| X_t \in \{-3\epsilon,3\epsilon\} \}$. Now, define a stochastic process ![]() $(U_t)_{t \geq \tau}$ started on
$(U_t)_{t \geq \tau}$ started on ![]() $\mathcal{F}_{\tau}$ that satisfies (13) or (9) with
$\mathcal{F}_{\tau}$ that satisfies (13) or (9) with ![]() $U_\tau =-2\epsilon$. From Proposition 2.1, we see that
$U_\tau =-2\epsilon$. From Proposition 2.1, we see that ![]() $ U_t<X_t$ for all
$ U_t<X_t$ for all ![]() $t\in (\tau,\tau') $. Now we can see that
$t\in (\tau,\tau') $. Now we can see that ![]() $ \mathbb{P} (\tau ' =\infty)= 0$. Indeed,
$ \mathbb{P} (\tau ' =\infty)= 0$. Indeed,
Proof of Theorem 1.3 Part 1. Suppose ![]() $\mathcal{N}=(-3\epsilon, 3\epsilon)$ for
$\mathcal{N}=(-3\epsilon, 3\epsilon)$ for ![]() $\epsilon>0$. Without loss of generality and for the purposes of this proof, assume that
$\epsilon>0$. Without loss of generality and for the purposes of this proof, assume that
 \begin{equation*}\epsilon<\min \left(\left( \frac{C(1)}{k} \right)^{\frac{1}{k-1}} , \left( \frac{C(c)}{k} \right)^{\frac{1}{k-1}} \right).\end{equation*}
\begin{equation*}\epsilon<\min \left(\left( \frac{C(1)}{k} \right)^{\frac{1}{k-1}} , \left( \frac{C(c)}{k} \right)^{\frac{1}{k-1}} \right).\end{equation*}
Pick a time z such that
for all ![]() $ t\geq z $, and define
$ t\geq z $, and define ![]() $\tau=\inf\{ t\geq z| X_t \in (-\epsilon,\epsilon) \}$ and
$\tau=\inf\{ t\geq z| X_t \in (-\epsilon,\epsilon) \}$ and ![]() $\tau'=\inf\{t>\tau| X_t \in \{-3\epsilon,3\epsilon\} \}$. From Proposition 5.1,
$\tau'=\inf\{t>\tau| X_t \in \{-3\epsilon,3\epsilon\} \}$. From Proposition 5.1, ![]() $\tau<\infty$ with positive probability. Now we define two stochastic processes
$\tau<\infty$ with positive probability. Now we define two stochastic processes ![]() $(Y_t)_{t\geq \tau}, (Y'_t)_{t \geq \tau}$ in the same probability space as
$(Y_t)_{t\geq \tau}, (Y'_t)_{t \geq \tau}$ in the same probability space as ![]() $X_t$ started on
$X_t$ started on ![]() $\mathcal{F}_\tau$, that satisfy (12) with drift constants 1 and c respectively. From Proposition 2.1, we see that if
$\mathcal{F}_\tau$, that satisfy (12) with drift constants 1 and c respectively. From Proposition 2.1, we see that if ![]() $Y_\tau>X_\tau>Y'_\tau$, then
$Y_\tau>X_\tau>Y'_\tau$, then ![]() $Y_t>X_t>Y'_t$ for all
$Y_t>X_t>Y'_t$ for all ![]() $ t \in (\tau, \tau')$. We set
$ t \in (\tau, \tau')$. We set ![]() $Y'_\tau$ such that
$Y'_\tau$ such that ![]() $X_\tau>Y'_\tau $, and
$X_\tau>Y'_\tau $, and
 \begin{equation*}Z^{Y'}_t=-\frac{Y'_t}{h(t)} >\max \left(-\left( \frac{C(1)}{k} \right)^{\frac{1}{k-1}} , -\left( \frac{C(c)}{k} \right)^{\frac{1}{k-1}} \right).\end{equation*}
\begin{equation*}Z^{Y'}_t=-\frac{Y'_t}{h(t)} >\max \left(-\left( \frac{C(1)}{k} \right)^{\frac{1}{k-1}} , -\left( \frac{C(c)}{k} \right)^{\frac{1}{k-1}} \right).\end{equation*}
Now we need to show that ![]() $\{\tau'=\infty\}\cap\{Y_t\rightarrow 0\} \cap \{Y'_t\rightarrow 0\} $ is nontrivial. Take
$\{\tau'=\infty\}\cap\{Y_t\rightarrow 0\} \cap \{Y'_t\rightarrow 0\} $ is nontrivial. Take ![]() $\epsilon_1$ and
$\epsilon_1$ and ![]() $\epsilon_c$, both less than
$\epsilon_c$, both less than ![]() $\epsilon$, as in the statement of Lemma 4.1 for
$\epsilon$, as in the statement of Lemma 4.1 for ![]() $Y_t$ and
$Y_t$ and ![]() $Y'_t$ respectively, and pick
$Y'_t$ respectively, and pick ![]() $\epsilon '= \min (\epsilon_1, \epsilon_c )$. For
$\epsilon '= \min (\epsilon_1, \epsilon_c )$. For ![]() $\epsilon '$, using Lemma 4.1, we know we can find
$\epsilon '$, using Lemma 4.1, we know we can find ![]() $\delta_1$ and
$\delta_1$ and ![]() $\delta_c$ such that on
$\delta_c$ such that on
we have ![]() $Y_s\rightarrow 0$, and on
$Y_s\rightarrow 0$, and on
we have ![]() $Y'_s\rightarrow 0$. From here, since
$Y'_s\rightarrow 0$. From here, since ![]() $A_1\cap A_c$ is nontrivial, we only need to argue that
$A_1\cap A_c$ is nontrivial, we only need to argue that ![]() $ \{\tau'=\infty\} \supset A\cap A_c $. From the remark of Lemma 4.1 we see that
$ \{\tau'=\infty\} \supset A\cap A_c $. From the remark of Lemma 4.1 we see that ![]() $Y_t$ and
$Y_t$ and ![]() $Y'_t$ always stay below 0 on
$Y'_t$ always stay below 0 on ![]() $A_1\cap A_c$. Also, from Proposition 4.5, we see that
$A_1\cap A_c$. Also, from Proposition 4.5, we see that
Equivalently, and using that
we have
 \begin{align*} Y'_t &> 2h(t)\left(\frac{C(c)}{k} \right)^{\frac{1}{k-1}} \\ &\geq -3\epsilon. \end{align*}
\begin{align*} Y'_t &> 2h(t)\left(\frac{C(c)}{k} \right)^{\frac{1}{k-1}} \\ &\geq -3\epsilon. \end{align*}
We now prove the second part of Theorem 1.3.
Proof of Theorem 1.3 Part 2. Let ![]() $\mathcal{N}= (-3\epsilon, 0).$ Define
$\mathcal{N}= (-3\epsilon, 0).$ Define ![]() $\tau=\inf \{t\geq 1 | X_t \in (-\frac{3\epsilon}{2},-\frac{5\epsilon}{4}) \}$, and let the exit time from
$\tau=\inf \{t\geq 1 | X_t \in (-\frac{3\epsilon}{2},-\frac{5\epsilon}{4}) \}$, and let the exit time from ![]() $\mathcal{N}$ be
$\mathcal{N}$ be ![]() $\tau_e=\inf \{t | X_t \not \in (-3\epsilon,0) \}$. From Proposition 5.1, we have that
$\tau_e=\inf \{t | X_t \not \in (-3\epsilon,0) \}$. From Proposition 5.1, we have that ![]() $\tau <\infty$ holds with positive probability. Define
$\tau <\infty$ holds with positive probability. Define ![]() $(Y_t)_{\tau \leq t\leq \tau_e }, (Y'_t)_{\tau \leq t\leq \tau_e}$ to be two processes that satisfy (9) with constants
$(Y_t)_{\tau \leq t\leq \tau_e }, (Y'_t)_{\tau \leq t\leq \tau_e}$ to be two processes that satisfy (9) with constants ![]() $k_1,k_2$ respectively. Suppose that
$k_1,k_2$ respectively. Suppose that ![]() $Y_\tau<X_\tau<Y'_\tau$ and
$Y_\tau<X_\tau<Y'_\tau$ and ![]() $Y_\tau,Y'_\tau \in (-2\epsilon,-\epsilon)$. Then by Proposition 2.1, we get
$Y_\tau,Y'_\tau \in (-2\epsilon,-\epsilon)$. Then by Proposition 2.1, we get ![]() $Y_t<X_t<Y'_t$ for all
$Y_t<X_t<Y'_t$ for all ![]() $t \in (\tau,\tau_e)$. Now, using Proposition 3.4, there is an event A such that
$t \in (\tau,\tau_e)$. Now, using Proposition 3.4, there is an event A such that ![]() $Y_t,Y'_t \in (-3\epsilon,0)$ for all
$Y_t,Y'_t \in (-3\epsilon,0)$ for all ![]() $t\geq \tau$. Consequently,
$t\geq \tau$. Consequently, ![]() $X_t\in (-3\epsilon,0)$ for all
$X_t\in (-3\epsilon,0)$ for all ![]() $t\geq \tau$, since
$t\geq \tau$, since ![]() $\tau_e=\infty$ on A. Finally, using Lemma 2.2 we conclude that
$\tau_e=\infty$ on A. Finally, using Lemma 2.2 we conclude that ![]() $Y_t\rightarrow 0$ on A; hence also
$Y_t\rightarrow 0$ on A; hence also ![]() $X_t\rightarrow 0$ on A.
$X_t\rightarrow 0$ on A.
6. The discrete model
6.1. Analysis of  $X_t$ when
$X_t$ when  $\frac{1}{2} + \frac{1}{2k} > \gamma $,
$\frac{1}{2} + \frac{1}{2k} > \gamma $,  $k>1$, and
$k>1$, and  $\gamma\in(1/2,1)$
$\gamma\in(1/2,1)$
Before proving Theorem 1.4, as described in Section 1.2, we assume that ![]() $X_n$ satisfies
$X_n$ satisfies
where the ![]() $Y_n$ are a.s. bounded and
$Y_n$ are a.s. bounded and ![]() $\mathbb{E}(Y_{n+1}|\mathcal{F}_n)=0$. In this section we additionally require
$\mathbb{E}(Y_{n+1}|\mathcal{F}_n)=0$. In this section we additionally require ![]() $Y_n$ to satisfy
$Y_n$ to satisfy ![]() $ \mathbb{E}(Y_{n+1}^2|\mathcal{F}_n )\geq l>0 $.
$ \mathbb{E}(Y_{n+1}^2|\mathcal{F}_n )\geq l>0 $.
Theorem 6.1. Let ![]() $(X_n)_{n\geq 1}$ solve (29). When
$(X_n)_{n\geq 1}$ solve (29). When ![]() $1/2 + 1/2k >\gamma$,
$1/2 + 1/2k >\gamma$, ![]() $X_t\rightarrow \infty$ a.s. Now we develop the necessary tools to prove this theorem.
$X_t\rightarrow \infty$ a.s. Now we develop the necessary tools to prove this theorem.
Proposition 6.1. The process ![]() $(X_n)_{n\geq 1}$ gets close to the origin infinitely often. More specifically, for
$(X_n)_{n\geq 1}$ gets close to the origin infinitely often. More specifically, for ![]() $\beta<0$ the event
$\beta<0$ the event ![]() $\{X_n \geq \beta n^{\frac{1-2\gamma}{2} } \text{\ i.o.} \} $ has probability 1.
$\{X_n \geq \beta n^{\frac{1-2\gamma}{2} } \text{\ i.o.} \} $ has probability 1.
Proof. From the restrictions on k we obtain
Set ![]() $h(t) = -t^{ \frac{1-\gamma}{1-k} }$, and define
$h(t) = -t^{ \frac{1-\gamma}{1-k} }$, and define ![]() $Z_n = -\frac{X_n}{h_n} $. From here, on the event
$Z_n = -\frac{X_n}{h_n} $. From here, on the event ![]() $\{X_m<0 \text{\,for\,all\,} m \geq n\}$, we get the following recursion:
$\{X_m<0 \text{\,for\,all\,} m \geq n\}$, we get the following recursion:
 \begin{align} Z_{n+1}-Z_{n} & \geq-\frac{X_{n+1} }{h(n+1)} +\frac{X_{n} }{h(n)}\\
&\geq-X_n\left(\frac{1}{h(n+1)} - \frac{1}{h(n)} \right ) - \frac{ |X_n|^k }{n^\gamma h(n+1) } - \frac{ Y_{n+1} }{n^\gamma h(n+1)} \nonumber\\
&\geq X_n \frac{1-\gamma}{ k-1 } \xi_n ^{ -\frac{1-\gamma}{ 1-k }-1 }- \frac{ |X_n|^k }{n^{\gamma} h(n+1) }-\frac{ Y_{n+1} }{n^\gamma h(n+1)}, \text{where }\xi_n\in \left(n,n+1\right)\nonumber \\
&\geq \frac{ X_n }{h(n+1) n^\gamma} \left(\frac{1-\gamma}{ k-1 } \xi_n ^{ -\frac{1-\gamma}{ 1-k }-1 } h(n+1)n^\gamma-\frac{|X_n|^k }{X_n} \right) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}\nonumber
\end{align}
\begin{align} Z_{n+1}-Z_{n} & \geq-\frac{X_{n+1} }{h(n+1)} +\frac{X_{n} }{h(n)}\\
&\geq-X_n\left(\frac{1}{h(n+1)} - \frac{1}{h(n)} \right ) - \frac{ |X_n|^k }{n^\gamma h(n+1) } - \frac{ Y_{n+1} }{n^\gamma h(n+1)} \nonumber\\
&\geq X_n \frac{1-\gamma}{ k-1 } \xi_n ^{ -\frac{1-\gamma}{ 1-k }-1 }- \frac{ |X_n|^k }{n^{\gamma} h(n+1) }-\frac{ Y_{n+1} }{n^\gamma h(n+1)}, \text{where }\xi_n\in \left(n,n+1\right)\nonumber \\
&\geq \frac{ X_n }{h(n+1) n^\gamma} \left(\frac{1-\gamma}{ k-1 } \xi_n ^{ -\frac{1-\gamma}{ 1-k }-1 } h(n+1)n^\gamma-\frac{|X_n|^k }{X_n} \right) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}\nonumber
\end{align}
where
 \begin{equation} a_n = \frac{ \xi_n ^{\frac{ -(1-\gamma)}{1-k} -1 } h(n+1)n^{\gamma} }{ -|h(n) |^{k-1} } . \end{equation}
\begin{equation} a_n = \frac{ \xi_n ^{\frac{ -(1-\gamma)}{1-k} -1 } h(n+1)n^{\gamma} }{ -|h(n) |^{k-1} } . \end{equation}
To justify the inequality (32), for large enough n, notice that ![]() $a_n \rightarrow 1$.
$a_n \rightarrow 1$.
Define
 \begin{equation*}{G'}_{s,n}=\sum_{ i=s}^{n-1} \frac{Y{i+1}}{i^{\gamma}h(i+1) } .\end{equation*}
\begin{equation*}{G'}_{s,n}=\sum_{ i=s}^{n-1} \frac{Y{i+1}}{i^{\gamma}h(i+1) } .\end{equation*}
We will see that ![]() ${G'}_{1,n}$ grows big enough so that
${G'}_{1,n}$ grows big enough so that ![]() $Z_n$ must, at certain times, get close enough to the origin so that
$Z_n$ must, at certain times, get close enough to the origin so that ![]() $X_n$ surpasses a constant multiple of h(n). To this end, we have the following lemma.
$X_n$ surpasses a constant multiple of h(n). To this end, we have the following lemma.
Lemma 6.1. ![]() $\limsup_{ n \rightarrow \infty} {G'}_{1,n} = \infty$ a.s.
$\limsup_{ n \rightarrow \infty} {G'}_{1,n} = \infty$ a.s.
We use the following theorem; for a reference see [Reference FisherFis92, Theorem 1, p. 676].
Theorem 6.2. Let ![]() $X_n$ be a martingale difference such that
$X_n$ be a martingale difference such that ![]() $\mathbb{E}(X_i^2|\mathcal{F}_{i-1}) <\infty$. Set
$\mathbb{E}(X_i^2|\mathcal{F}_{i-1}) <\infty$. Set ![]() $s_n^2=\sum_{i=1}^{n}\mathbb{E}(X_i^2|\mathcal{F}_{i-1})$, and define
$s_n^2=\sum_{i=1}^{n}\mathbb{E}(X_i^2|\mathcal{F}_{i-1})$, and define ![]() $\phi(x) = ( 2\log_2(x^2\vee e^2) )^{\frac{1}{2} }$. We assume that
$\phi(x) = ( 2\log_2(x^2\vee e^2) )^{\frac{1}{2} }$. We assume that ![]() $s_n\rightarrow \infty$ a.s. and that
$s_n\rightarrow \infty$ a.s. and that ![]() $|X_i|\leq \frac{K_i s_i}{\phi(s_i)}$ a.s., where
$|X_i|\leq \frac{K_i s_i}{\phi(s_i)}$ a.s., where ![]() $K_i$ is
$K_i$ is ![]() $\mathcal{F}_{i-1}$-measurable with
$\mathcal{F}_{i-1}$-measurable with ![]() $ \limsup_{i \rightarrow \infty} K_i <K$ for some constant K. Then there is a positive constant
$ \limsup_{i \rightarrow \infty} K_i <K$ for some constant K. Then there is a positive constant ![]() $\epsilon(K)$ such that
$\epsilon(K)$ such that
![]() $\limsup_{n \rightarrow \infty}\sum_{i=1}^{n} \frac{X_i}{s_n\phi(s_n) }\geq \epsilon(K) $ a.s.
$\limsup_{n \rightarrow \infty}\sum_{i=1}^{n} \frac{X_i}{s_n\phi(s_n) }\geq \epsilon(K) $ a.s.
It is clear that ![]() ${G'_{ 1,n }}$ satisfies all the hypotheses required for the aforementioned theorem to hold.
${G'_{ 1,n }}$ satisfies all the hypotheses required for the aforementioned theorem to hold.
From Lemma 6.1, it is immediate that for any random time s (not necessarily a stopping time), ![]() $\limsup_{n\rightarrow \infty} {G'}_{s,n} = \infty $ a.s.
$\limsup_{n\rightarrow \infty} {G'}_{s,n} = \infty $ a.s.
Now, we return to the proof of Proposition 6.1. Assume that there is ![]() $n_0$ such that
$n_0$ such that
for all ![]() $n\geq n_0$. Then, since
$n\geq n_0$. Then, since ![]() $ \frac{|x|^k}{x}$ is increasing, we get that
$ \frac{|x|^k}{x}$ is increasing, we get that
Therefore,
So
 \begin{align*} Z_n&\geq Z_{n_0} +\sum_{i=n_0}^{n}\frac{ X_i }{h(i+1)i^\gamma} \left(\frac{2(1-\gamma)}{ k-1 } |h(i)|^{k-1}-\frac{|X_i|^k }{X_i} \right)+{G'}_{n_0,n} \\ &> Z_{n_0}+ {G'}_{n_0,n}, \end{align*}
\begin{align*} Z_n&\geq Z_{n_0} +\sum_{i=n_0}^{n}\frac{ X_i }{h(i+1)i^\gamma} \left(\frac{2(1-\gamma)}{ k-1 } |h(i)|^{k-1}-\frac{|X_i|^k }{X_i} \right)+{G'}_{n_0,n} \\ &> Z_{n_0}+ {G'}_{n_0,n}, \end{align*}
which gives ![]() $ \limsup_{n \rightarrow \infty}Z_n = \infty $. This is a contradiction, since it would imply
$ \limsup_{n \rightarrow \infty}Z_n = \infty $. This is a contradiction, since it would imply ![]() $X_n \geq 0$ infinitely often.
$X_n \geq 0$ infinitely often.
Since ![]() $ n^{\frac{1-\gamma}{1-k}} = o( n^{\frac{1-2\gamma}{2} })$, for every constant
$ n^{\frac{1-\gamma}{1-k}} = o( n^{\frac{1-2\gamma}{2} })$, for every constant ![]() $\beta<0$ the event
$\beta<0$ the event ![]() $\{ X_n \geq \beta n^{ \frac{1-2\gamma}{ 2} } \text{\,i.o.} \} $ holds a.s.
$\{ X_n \geq \beta n^{ \frac{1-2\gamma}{ 2} } \text{\,i.o.} \} $ holds a.s.
We define ![]() $ G_{n,u}=\sum_{ i=n}^{u-1} \frac{Y_{i+1}}{i^{\gamma} } $; this is an important quantity for the next lemma and the remainder of the section.
$ G_{n,u}=\sum_{ i=n}^{u-1} \frac{Y_{i+1}}{i^{\gamma} } $; this is an important quantity for the next lemma and the remainder of the section.
Lemma 6.2. For any n, we can find ![]() $a_1>0, \delta>0$ such that
$a_1>0, \delta>0$ such that ![]() $ \mathbb{P}(\sup_{u\geq n}G_{{n},u}\geq a_1 n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )> \delta $ and
$ \mathbb{P}(\sup_{u\geq n}G_{{n},u}\geq a_1 n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )> \delta $ and ![]() $ \mathbb{P}(G_{n,\infty}\geq a_1 n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )>\delta$.
$ \mathbb{P}(G_{n,\infty}\geq a_1 n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )>\delta$.
Proof. Define ![]() $\tau = \inf \{u\geq n| G_{n,u} \notin (-a_2n^{\frac{1-2\gamma}{2}},a_2n^{\frac{1-2\gamma}{2}} ) \} $. We calculate the stopped variance of
$\tau = \inf \{u\geq n| G_{n,u} \notin (-a_2n^{\frac{1-2\gamma}{2}},a_2n^{\frac{1-2\gamma}{2}} ) \} $. We calculate the stopped variance of ![]() $ G_{\tau} \,{:}\,{\raise-1.5pt{=}}\, G_{n,\tau}$. We will do so recursively; fix
$ G_{\tau} \,{:}\,{\raise-1.5pt{=}}\, G_{n,\tau}$. We will do so recursively; fix ![]() $m\geq n$ and calculate as follows:
$m\geq n$ and calculate as follows:
 \begin{align*} \mathbb{E} (( G_{ \tau \wedge {m+1} } ) ^2 |\mathcal{F}_n )-\mathbb{E} ( G_{\tau \wedge m} )^2 |\mathcal{F}_n )&= \mathbb{E} \left(1_{\tau>m} \left(2\frac{Y_{m+1}}{m^\gamma } G_{m} +\frac{ Y_{m+1}^2}{m^{2\gamma}} \right) |\mathcal{F}_n \right) \\ &=\mathbb{E} \left(1_{\tau>m} 2\frac{Y_{m+1}}{m^\gamma } G_{m}|\mathcal{F}_n \right) +\mathbb{E}\left(1_{\tau>m}\frac{ Y_{m+1}^2}{m^{2\gamma}} |\mathcal{F}_n \right) \\ &=0 + \mathbb{E}\left(1_{[\tau>m]} \mathbb{E}\left(\frac{ Y_{m+1}^2}{m^{2\gamma}} |\mathcal{F}_{m} \right) |\mathcal{F}_n \right)\\ &\geq \epsilon \frac{1}{m^{2\gamma}} \mathbb{E}(1_{[\tau>m]} |\mathcal{F}_n )\\ &\geq \epsilon \frac{1}{m^{2\gamma}} \mathbb{P}(\tau=\infty |\mathcal{F}_n ) . \end{align*}
\begin{align*} \mathbb{E} (( G_{ \tau \wedge {m+1} } ) ^2 |\mathcal{F}_n )-\mathbb{E} ( G_{\tau \wedge m} )^2 |\mathcal{F}_n )&= \mathbb{E} \left(1_{\tau>m} \left(2\frac{Y_{m+1}}{m^\gamma } G_{m} +\frac{ Y_{m+1}^2}{m^{2\gamma}} \right) |\mathcal{F}_n \right) \\ &=\mathbb{E} \left(1_{\tau>m} 2\frac{Y_{m+1}}{m^\gamma } G_{m}|\mathcal{F}_n \right) +\mathbb{E}\left(1_{\tau>m}\frac{ Y_{m+1}^2}{m^{2\gamma}} |\mathcal{F}_n \right) \\ &=0 + \mathbb{E}\left(1_{[\tau>m]} \mathbb{E}\left(\frac{ Y_{m+1}^2}{m^{2\gamma}} |\mathcal{F}_{m} \right) |\mathcal{F}_n \right)\\ &\geq \epsilon \frac{1}{m^{2\gamma}} \mathbb{E}(1_{[\tau>m]} |\mathcal{F}_n )\\ &\geq \epsilon \frac{1}{m^{2\gamma}} \mathbb{P}(\tau=\infty |\mathcal{F}_n ) . \end{align*}
Therefore,
 \begin{align} E (( G_{ \tau \wedge {m} } ) ^2 |\mathcal{F}_n )&\geq \mathbb{E} ( (G_{\tau \wedge n } )^2 |\mathcal{F}_n )+c\mathbb{P}(\tau=\infty |\mathcal{F}_n ) (n^{1-2\gamma} -(m-1)^{1-2\gamma} )\nonumber\\ &= c\mathbb{P}(\tau=\infty |\mathcal{F}_n ) (n^{1-2\gamma} -(m-1)^{1-2\gamma} ). \end{align}
\begin{align} E (( G_{ \tau \wedge {m} } ) ^2 |\mathcal{F}_n )&\geq \mathbb{E} ( (G_{\tau \wedge n } )^2 |\mathcal{F}_n )+c\mathbb{P}(\tau=\infty |\mathcal{F}_n ) (n^{1-2\gamma} -(m-1)^{1-2\gamma} )\nonumber\\ &= c\mathbb{P}(\tau=\infty |\mathcal{F}_n ) (n^{1-2\gamma} -(m-1)^{1-2\gamma} ). \end{align}
Notice that since the ![]() $Y_n$ are a.s. bounded,
$Y_n$ are a.s. bounded, ![]() $|G_\tau| \leq a_2 n^{\frac{1-2\gamma}{2} } +\frac{M}{n^{\gamma}}$, and since
$|G_\tau| \leq a_2 n^{\frac{1-2\gamma}{2} } +\frac{M}{n^{\gamma}}$, and since ![]() $\gamma > \gamma-1/2$, we get that
$\gamma > \gamma-1/2$, we get that ![]() $|G_\tau| \leq 2a_2n^{\frac{1-2\gamma}{2} } $ for n large enough. For m large, we can find a constant c such that
$|G_\tau| \leq 2a_2n^{\frac{1-2\gamma}{2} } $ for n large enough. For m large, we can find a constant c such that ![]() $n^{1-2\gamma} -(m-1)^{1-2\gamma} \geq c'n^{1-2\gamma}$. Using (34), we obtain
$n^{1-2\gamma} -(m-1)^{1-2\gamma} \geq c'n^{1-2\gamma}$. Using (34), we obtain
Choosing ![]() $a_2$ small enough, we may conclude
$a_2$ small enough, we may conclude ![]() $\mathbb{P} ( \tau < \infty | \mathcal{F}_n) > 1/2 $ for all n large enough.
$\mathbb{P} ( \tau < \infty | \mathcal{F}_n) > 1/2 $ for all n large enough.
Now we take any martingale ![]() $M_n$ starting at 0 such that it exits an interval
$M_n$ starting at 0 such that it exits an interval ![]() $ (-2a,2a) $ with probability at least p, and
$ (-2a,2a) $ with probability at least p, and ![]() $|M_{n+1}-M_n|< a $ a.s. Then we stop the martingale upon exiting the interval
$|M_{n+1}-M_n|< a $ a.s. Then we stop the martingale upon exiting the interval ![]() $(-2a,2a)$; that is, define
$(-2a,2a)$; that is, define ![]() $\tau_{-}$ to be the first time
$\tau_{-}$ to be the first time ![]() $M_n$ goes below
$M_n$ goes below ![]() $-2a$ and
$-2a$ and ![]() $\tau_{+}$ to be the first time that
$\tau_{+}$ to be the first time that ![]() $M_n$ surpasses 2a, and set
$M_n$ surpasses 2a, and set ![]() $\tau = \tau_{-} \wedge \tau_{+}$. Using the optimal stopping theorem for the bounded martingale
$\tau = \tau_{-} \wedge \tau_{+}$. Using the optimal stopping theorem for the bounded martingale ![]() $M_{\tau \wedge n}$ and taking n to infinity, we obtain
$M_{\tau \wedge n}$ and taking n to infinity, we obtain
So ![]() $ \mathbb{P}(\tau_{-}> \tau_{+} ) \geq \dfrac{4p-2}{5} $, which implies that
$ \mathbb{P}(\tau_{-}> \tau_{+} ) \geq \dfrac{4p-2}{5} $, which implies that ![]() $\mathbb{P}(\sup_{n} M_n \geq 2a ) \geq \dfrac{4p-2}{5}$.
$\mathbb{P}(\sup_{n} M_n \geq 2a ) \geq \dfrac{4p-2}{5}$.
The previous argument applied to ![]() $G_{n,u}$, given
$G_{n,u}$, given ![]() $\mathcal{F}_n$, concludes the proof of the first part of the lemma. Indeed, since the probability p of exiting the interval is bigger than
$\mathcal{F}_n$, concludes the proof of the first part of the lemma. Indeed, since the probability p of exiting the interval is bigger than ![]() $1/2$, we may deduce that
$1/2$, we may deduce that ![]() $\dfrac{4p-2}{5}>0$.
$\dfrac{4p-2}{5}>0$.
For the second part of the lemma, we use the following inequality: let ![]() $M_n$ be a martingale such that
$M_n$ be a martingale such that ![]() $M_0=0$ and
$M_0=0$ and ![]() $\mathbb{E}(M_n^2) <\infty$. Then
$\mathbb{E}(M_n^2) <\infty$. Then
(for a reference see [Reference DurrettDur13, Exercise 5.4.5, p. 213]). Let ![]() $\tau$ be the first time
$\tau$ be the first time ![]() $G_{n,u}$ surpasses
$G_{n,u}$ surpasses ![]() $ a_2 n^{1-2\gamma} $. Condition on
$ a_2 n^{1-2\gamma} $. Condition on ![]() $[\tau < \infty]$, and notice that
$[\tau < \infty]$, and notice that ![]() $G_{n,\infty}> \frac{a_2}{2}n^{1-2\gamma}$ when
$G_{n,\infty}> \frac{a_2}{2}n^{1-2\gamma}$ when ![]() $\inf_{ u\geq \tau}G_{\tau,u} > -\frac{a_2}{2}n^{1-2\gamma}$. Using the previous inequality and the fact that
$\inf_{ u\geq \tau}G_{\tau,u} > -\frac{a_2}{2}n^{1-2\gamma}$. Using the previous inequality and the fact that ![]() $\frac{x}{x+1}$ is increasing, we obtain
$\frac{x}{x+1}$ is increasing, we obtain
 \begin{align*} \mathbb{P}(G_{n,\infty}\leq \frac{a_2}{2}n^{\frac{1-2\gamma}{2}} |\mathcal{F}_{\tau},[\tau <\infty] ) &\leq \mathbb{P}( \inf_{ u\geq \tau}G_{\tau,u} \leq -\frac{a_2}{2}n^{1-2\gamma} |\mathcal{F}_{\tau},[\tau <\infty] ) \\[4pt]
&\leq \frac{ \mathbb{E}((G_{\tau,\infty} )^2 |\mathcal{F}_{\tau},[\tau <\infty] )}{\mathbb{E}((G_{\tau,\infty} )^2 |\mathcal{F}_{\tau},[\tau <\infty])+ \frac{a_2^2}{4}n^{1-2\gamma }} \\[4pt]
&\leq\frac{ c\tau ^{1-2\gamma } }{ c\tau ^{1-2\gamma } + \frac{a_2^2}{4}n^{1-2\gamma } } \\[4pt]
&\leq \frac{ c }{ c + \frac{a_2^2}{4} }. \end{align*}
\begin{align*} \mathbb{P}(G_{n,\infty}\leq \frac{a_2}{2}n^{\frac{1-2\gamma}{2}} |\mathcal{F}_{\tau},[\tau <\infty] ) &\leq \mathbb{P}( \inf_{ u\geq \tau}G_{\tau,u} \leq -\frac{a_2}{2}n^{1-2\gamma} |\mathcal{F}_{\tau},[\tau <\infty] ) \\[4pt]
&\leq \frac{ \mathbb{E}((G_{\tau,\infty} )^2 |\mathcal{F}_{\tau},[\tau <\infty] )}{\mathbb{E}((G_{\tau,\infty} )^2 |\mathcal{F}_{\tau},[\tau <\infty])+ \frac{a_2^2}{4}n^{1-2\gamma }} \\[4pt]
&\leq\frac{ c\tau ^{1-2\gamma } }{ c\tau ^{1-2\gamma } + \frac{a_2^2}{4}n^{1-2\gamma } } \\[4pt]
&\leq \frac{ c }{ c + \frac{a_2^2}{4} }. \end{align*}
Therefore,
 \begin{equation*}\mathbb{P}(G_{n,\infty}\geq \frac{a_2}{2} n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n ) \geq \mathbb{P} (\tau <\infty) \frac{ \frac{a_2^2}{4} } { c + \frac{a_2^2}{4} }, \end{equation*}
\begin{equation*}\mathbb{P}(G_{n,\infty}\geq \frac{a_2}{2} n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n ) \geq \mathbb{P} (\tau <\infty) \frac{ \frac{a_2^2}{4} } { c + \frac{a_2^2}{4} }, \end{equation*}
which concludes the proof.
For any stopping time ![]() $\sigma$, we get the following version of the previous lemma.
$\sigma$, we get the following version of the previous lemma.
Lemma 6.3. For any n, we can find ![]() $a_1>0,\delta_1>0,\delta_2>0$ such that
$a_1>0,\delta_1>0,\delta_2>0$ such that ![]() $ \mathbb{P}(\sup_{u\geq \sigma}G_{\sigma,u}\geq a_1 \sigma^{ \frac{1-2\gamma}{2}} |\mathcal{F}_\sigma )> \delta_1 $ and
$ \mathbb{P}(\sup_{u\geq \sigma}G_{\sigma,u}\geq a_1 \sigma^{ \frac{1-2\gamma}{2}} |\mathcal{F}_\sigma )> \delta_1 $ and ![]() $ \mathbb{P}(G_{\sigma,\infty}\geq a_1 \sigma^{ \frac{1-2\gamma}{2}} |\mathcal{F}_\sigma )>\delta_2$.
$ \mathbb{P}(G_{\sigma,\infty}\geq a_1 \sigma^{ \frac{1-2\gamma}{2}} |\mathcal{F}_\sigma )>\delta_2$.
Corollary 6.1. The event ![]() $\{ X_n \geq 0 \text{\ i.o.}\}$ holds a.s.
$\{ X_n \geq 0 \text{\ i.o.}\}$ holds a.s.
Proof. For any m, n we get the lower bound ![]() $ X_m-X_n \geq G_{n,m} $. Now, we define an increasing sequence of stopping times
$ X_m-X_n \geq G_{n,m} $. Now, we define an increasing sequence of stopping times ![]() $\tau_n$, going to infinity a.s., such that
$\tau_n$, going to infinity a.s., such that ![]() $X_{\tau_n} \geq \beta \tau_n^{\frac{1-2\gamma}{2} }$ for
$X_{\tau_n} \geq \beta \tau_n^{\frac{1-2\gamma}{2} }$ for ![]() $|\beta|<a_1$, where
$|\beta|<a_1$, where ![]() $a_1$ is such that
$a_1$ is such that ![]() $ \mathbb{P}\left(\sup_{u\geq \sigma}G_{\tau_n,u}\geq a_1 {\tau_n}^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} \right)> \delta_1 $, whose existence is guaranteed by Lemma 6.3. From Proposition 6.1, we can do so with all
$ \mathbb{P}\left(\sup_{u\geq \sigma}G_{\tau_n,u}\geq a_1 {\tau_n}^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} \right)> \delta_1 $, whose existence is guaranteed by Lemma 6.3. From Proposition 6.1, we can do so with all ![]() $\tau_n$ a.s. finite. Hence,
$\tau_n$ a.s. finite. Hence,
 \begin{align*} \mathbb{P}\left(\sup_{\infty \geq u\geq {\tau_n}} X_u-X_{\tau_n}\geq a_1{\tau_n}^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} \right) &\geq \mathbb{P}\left(\sup_{\infty \geq u\geq {\tau_n} } G_{\tau_n,u } \geq a_1 {\tau_n}^{ \frac{1-2\gamma}{2} }|\mathcal{F}_{\tau_n} \right)\\ &>\delta_1 >0 . \end{align*}
\begin{align*} \mathbb{P}\left(\sup_{\infty \geq u\geq {\tau_n}} X_u-X_{\tau_n}\geq a_1{\tau_n}^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} \right) &\geq \mathbb{P}\left(\sup_{\infty \geq u\geq {\tau_n} } G_{\tau_n,u } \geq a_1 {\tau_n}^{ \frac{1-2\gamma}{2} }|\mathcal{F}_{\tau_n} \right)\\ &>\delta_1 >0 . \end{align*}
Therefore, by Borel–Cantelli on the event ![]() $\Big\{X_{\tau_n} \geq \beta \tau_n^{\frac{1-2\gamma}{2} } \text{\ i.o.} \Big \}$, we get
$\Big\{X_{\tau_n} \geq \beta \tau_n^{\frac{1-2\gamma}{2} } \text{\ i.o.} \Big \}$, we get ![]() $\{X_{\tau_n} \geq 0\ \text{\ i.o.} \}$. Therefore
$\{X_{\tau_n} \geq 0\ \text{\ i.o.} \}$. Therefore ![]() $\{X_n \geq 0\ \text{\ i.o.} \}$ holds a.s.
$\{X_n \geq 0\ \text{\ i.o.} \}$ holds a.s.
Proof of Theorem 6.1. Again we define an increasing sequence of stopping times ![]() $\tau_n$, going to infinity a.s., such that
$\tau_n$, going to infinity a.s., such that ![]() $X_{\tau_n} \geq 0$ this time. Since
$X_{\tau_n} \geq 0$ this time. Since ![]() $ \mathbb{P}(G_{\tau_n,\infty}\geq a_1 \tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} )>\delta_2$, an application of Borel–Cantelli shows that
$ \mathbb{P}(G_{\tau_n,\infty}\geq a_1 \tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_{\tau_n} )>\delta_2$, an application of Borel–Cantelli shows that ![]() $\{X_n\geq \frac{a_1}{2}n^{ \frac{1-2\gamma}{2}} \text{\ i.o.} \}$ holds a.s. We claim that a.s. there are constants
$\{X_n\geq \frac{a_1}{2}n^{ \frac{1-2\gamma}{2}} \text{\ i.o.} \}$ holds a.s. We claim that a.s. there are constants ![]() $c(\omega)>0$ and
$c(\omega)>0$ and ![]() $m(\omega) $ such that
$m(\omega) $ such that ![]() $\{ X_n > c \mathrm{ for all } n\geq m \}=\{\liminf_{n\to \infty} X_n> 0\}$. Indeed, if we define
$\{ X_n > c \mathrm{ for all } n\geq m \}=\{\liminf_{n\to \infty} X_n> 0\}$. Indeed, if we define ![]() $\tau_0=0$ and
$\tau_0=0$ and ![]() $\tau_{n+1} = \inf \{m>\tau_n+1| X_m \geq \frac{a_1}{2} m^{ \frac{1-2\gamma}{2}} \}$, we see that
$\tau_{n+1} = \inf \{m>\tau_n+1| X_m \geq \frac{a_1}{2} m^{ \frac{1-2\gamma}{2}} \}$, we see that ![]() $\tau_n<\infty$ a.s. and
$\tau_n<\infty$ a.s. and ![]() $\tau_n \rightarrow \infty.$ This gives a corresponding filtration, namely
$\tau_n \rightarrow \infty.$ This gives a corresponding filtration, namely ![]() $\mathcal{F}_n = \sigma( \tau_n)$.
$\mathcal{F}_n = \sigma( \tau_n)$.
To finish the claim, we show that ![]() $A=\{\liminf_{n\to \infty} X_n\leq 0\}$ has probability zero. To do so, it is sufficient to argue that there is a
$A=\{\liminf_{n\to \infty} X_n\leq 0\}$ has probability zero. To do so, it is sufficient to argue that there is a ![]() $\delta$ such that
$\delta$ such that ![]() $ \mathbb{P}( A|\mathcal{F}_n )<1-\delta $ a.s. for all
$ \mathbb{P}( A|\mathcal{F}_n )<1-\delta $ a.s. for all ![]() $n\geq 1$. This is immediate from the previous calculation. Indeed,
$n\geq 1$. This is immediate from the previous calculation. Indeed,
 \begin{align*} \mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P}\left(\liminf_{n } X_n \geq \frac{3a_1}{2}\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n \right)\\ &= 1-\mathbb{P} \left(\liminf_{n } X_n-\frac{a_1}{2} \tau_n^{ \frac{1-2\gamma}{2}} \geq a_1\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n \right) \\ &\leq 1-\mathbb{P} ( \liminf_{n }G_{\tau_n,n} \geq a_1\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )\\ &<1-\delta_2. \end{align*}
\begin{align*} \mathbb{P}( A|\mathcal{F}_n ) & \leq 1-\mathbb{P}\left(\liminf_{n } X_n \geq \frac{3a_1}{2}\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n \right)\\ &= 1-\mathbb{P} \left(\liminf_{n } X_n-\frac{a_1}{2} \tau_n^{ \frac{1-2\gamma}{2}} \geq a_1\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n \right) \\ &\leq 1-\mathbb{P} ( \liminf_{n }G_{\tau_n,n} \geq a_1\tau_n^{ \frac{1-2\gamma}{2}} |\mathcal{F}_n )\\ &<1-\delta_2. \end{align*}
The process ![]() $G_{m,\infty}$ is a.s. finite, and since the drift term
$G_{m,\infty}$ is a.s. finite, and since the drift term ![]() $\sum_{ i\geq n } \frac{|X_i|^k}{i^{\gamma}} \to \infty$, we get that
$\sum_{ i\geq n } \frac{|X_i|^k}{i^{\gamma}} \to \infty$, we get that ![]() $X_n \to \infty $.
$X_n \to \infty $.
Proof of Theorem 1.4. Define ![]() $\tau=\inf \{n| X_n \in (-\epsilon, \epsilon)\}$ and
$\tau=\inf \{n| X_n \in (-\epsilon, \epsilon)\}$ and ![]() $\tau ' =\inf \{n>\tau | X_n \not \in (-\epsilon ' , \epsilon ') \}$, where
$\tau ' =\inf \{n>\tau | X_n \not \in (-\epsilon ' , \epsilon ') \}$, where ![]() $\epsilon<\epsilon'$. When
$\epsilon<\epsilon'$. When ![]() $\epsilon$ is small enough, we may assume that
$\epsilon$ is small enough, we may assume that ![]() $\tau<\infty$ with positive probability; otherwise we have nothing to prove. On
$\tau<\infty$ with positive probability; otherwise we have nothing to prove. On ![]() $\{\tau<\infty \}$, couple
$\{\tau<\infty \}$, couple ![]() $X_n$ with
$X_n$ with ![]() $X'_n$ so that
$X'_n$ so that ![]() $\mathbb{P}(X_n=X'_n, \tau \leq n\leq \tau ' |[\tau <\infty] )=1 $, where
$\mathbb{P}(X_n=X'_n, \tau \leq n\leq \tau ' |[\tau <\infty] )=1 $, where ![]() $X_n'$ is a process that solves (29). Since
$X_n'$ is a process that solves (29). Since ![]() $X'_n\rightarrow \infty$ a.s., we have that
$X'_n\rightarrow \infty$ a.s., we have that ![]() $\tau' <\infty$ a.s. Thus, on
$\tau' <\infty$ a.s. Thus, on ![]() $\{\lim_{n \rightarrow \infty} X_n =0\} $, we have that
$\{\lim_{n \rightarrow \infty} X_n =0\} $, we have that ![]() $\{ X_n>\epsilon' \text{\ i.o.} \}$. Therefore,
$\{ X_n>\epsilon' \text{\ i.o.} \}$. Therefore, ![]() $\mathbb{P}(\lim_{n \rightarrow \infty} X_n =0) = 0$.
$\mathbb{P}(\lim_{n \rightarrow \infty} X_n =0) = 0$.
6.2. Analysis of  $X_t$ when
$X_t$ when  $\frac{1}{2} + \frac{1}{2k} < \gamma $,
$\frac{1}{2} + \frac{1}{2k} < \gamma $,  $k>1$, and
$k>1$, and  $\gamma\in(1/2,1)$
$\gamma\in(1/2,1)$
Before proving the main Theorem 1.5, as described in Section 1.2 we will study a process ![]() $(X_n)_{n \geq 1}$ that satisfies
$(X_n)_{n \geq 1}$ that satisfies
where ![]() $0 < f(x) \leq |x|^k$ when
$0 < f(x) \leq |x|^k$ when ![]() $ x\in(-\epsilon,\epsilon) $, and
$ x\in(-\epsilon,\epsilon) $, and ![]() $f(x) = |x|^k$ when
$f(x) = |x|^k$ when ![]() $ x\in\mathbb{R}\setminus (-\epsilon,\epsilon) $.
$ x\in\mathbb{R}\setminus (-\epsilon,\epsilon) $.
The analysis will again rely on studying the process ![]() $Z_{n}=-\frac{X_n}{h(n)}$, where
$Z_{n}=-\frac{X_n}{h(n)}$, where ![]() $h(t)= -t^{ \frac{1-\gamma}{1-k}}$. An important quantity related to the process
$h(t)= -t^{ \frac{1-\gamma}{1-k}}$. An important quantity related to the process ![]() $Z_n$ will be
$Z_n$ will be ![]() $G'_{s,n} = \sum_{i=s}^{n-1} \frac{Y_{i+1}}{i^{\gamma}h(i+1)} $.
$G'_{s,n} = \sum_{i=s}^{n-1} \frac{Y_{i+1}}{i^{\gamma}h(i+1)} $.
Recall that the ![]() $Y_n$ constitute martingale differences satisfying
$Y_n$ constitute martingale differences satisfying ![]() $|Y_n|<M$ almost surely. Furthermore, we find
$|Y_n|<M$ almost surely. Furthermore, we find ![]() $x_0<0$ such that
$x_0<0$ such that ![]() $f(x)>M$ for every
$f(x)>M$ for every ![]() $x\leq x_0$. We will make use of
$x\leq x_0$. We will make use of ![]() $x_0$ in the next lemma.
$x_0$ in the next lemma.
Lemma 6.4. Take ![]() $C= \max( M,|X_1|,|x_0| )$. Then
$C= \max( M,|X_1|,|x_0| )$. Then ![]() $X_n> -2C$ for all n, a.s.
$X_n> -2C$ for all n, a.s.
Proof. We can show this by induction. Of course ![]() $X_1> -2C$. For the inductive step, we distinguish two cases. First, assume that
$X_1> -2C$. For the inductive step, we distinguish two cases. First, assume that ![]() $-2C<X_n<-C$. Then
$-2C<X_n<-C$. Then
 \begin{align*} X_{n+1} &= X_n +\frac{f(X_n)}{n^\gamma} + \frac{Y_{n+1}}{n^{\gamma}} \\[4pt]
&\geq -2C + \frac{f(X_n)}{n^\gamma} -\frac{M}{n^{\gamma}}\\[4pt]
&> -2C. \end{align*}
\begin{align*} X_{n+1} &= X_n +\frac{f(X_n)}{n^\gamma} + \frac{Y_{n+1}}{n^{\gamma}} \\[4pt]
&\geq -2C + \frac{f(X_n)}{n^\gamma} -\frac{M}{n^{\gamma}}\\[4pt]
&> -2C. \end{align*}
Now, assume that ![]() $X_n\geq -C$. Then
$X_n\geq -C$. Then
 \begin{align*} X_{n+1} &= X_n +\frac{|X_n|^k}{n^\gamma} + \frac{Y_n}{n^{\gamma}} \\[4pt]
&\geq -C + 0 -\frac{M}{n^{\gamma}}\\[4pt]
&> -2C. \end{align*}
\begin{align*} X_{n+1} &= X_n +\frac{|X_n|^k}{n^\gamma} + \frac{Y_n}{n^{\gamma}} \\[4pt]
&\geq -C + 0 -\frac{M}{n^{\gamma}}\\[4pt]
&> -2C. \end{align*}
Pick ![]() $\epsilon >0$ such that
$\epsilon >0$ such that
 \begin{equation*} \epsilon \leq \min \left( \frac{1}{4}, \frac{1}{2} \left(\frac{1-\gamma}{3(k-1)}\right)^{ \frac{1}{k-1} } \right) .\end{equation*}
\begin{equation*} \epsilon \leq \min \left( \frac{1}{4}, \frac{1}{2} \left(\frac{1-\gamma}{3(k-1)}\right)^{ \frac{1}{k-1} } \right) .\end{equation*}
Let ![]() $a_n$ be defined as in Section 6.1, first appearing in (31) and defined in (33).
$a_n$ be defined as in Section 6.1, first appearing in (31) and defined in (33).
Claim: We can find ![]() $n_0$ that satisfies the following properties:
$n_0$ that satisfies the following properties:
1.
 $a_n >1/2$ for
$a_n >1/2$ for  $n\geq n_0$ a.s.
$n\geq n_0$ a.s.-
2. If
 $-\frac{X_{n+1}}{h(n+1)}>-2\epsilon$ and
$-\frac{X_{n+1}}{h(n+1)}>-2\epsilon$ and  $-\frac{X_{n}}{h(n)}\leq-2\epsilon$, then
$-\frac{X_{n}}{h(n)}\leq-2\epsilon$, then  $-\frac{X_{n+1}}{h(n+1)} <-\epsilon$, when
$-\frac{X_{n+1}}{h(n+1)} <-\epsilon$, when  $n\geq n_0$.
$n\geq n_0$. -
3.
 $\mathbb{P} ({G'}_{n_0,n} \in (\frac{-\epsilon}{2}, \frac{\epsilon}{2}) \forall n \geq n_0 |\mathcal{F}_{n_0} ) >0$.
$\mathbb{P} ({G'}_{n_0,n} \in (\frac{-\epsilon}{2}, \frac{\epsilon}{2}) \forall n \geq n_0 |\mathcal{F}_{n_0} ) >0$.
Proof.
1. This is trivial.
-
2. Recall that
 $h(t)=-t^{\frac{1-\gamma}{1-k}}$. Since
$h(t)=-t^{\frac{1-\gamma}{1-k}}$. Since  $|Y_n|<M$, and
$|Y_n|<M$, and  $X_n>-2C$ a.s., whenever
$X_n>-2C$ a.s., whenever  $X_n<0$ we have
$X_n<0$ we have  $|X_{n+1}-X_{n}|=O(n^{-\gamma})$. Also,
$|X_{n+1}-X_{n}|=O(n^{-\gamma})$. Also,  $ n^{-\gamma} = o(h(n) )$, since
$ n^{-\gamma} = o(h(n) )$, since  $\gamma > \frac{1-\gamma}{k-1}$. Indeed,
$\gamma > \frac{1-\gamma}{k-1}$. Indeed,  $\gamma > \frac{1-\gamma}{k-1}$ is equivalent to
$\gamma > \frac{1-\gamma}{k-1}$ is equivalent to  $ \gamma >1/k = 1/2k+1/2k$; however,
$ \gamma >1/k = 1/2k+1/2k$; however,  $ 1/2>1/2k$, and since
$ 1/2>1/2k$, and since  $\gamma > 1/2 + 1/2k$, we conclude. Furthermore, notice that
$\gamma > 1/2 + 1/2k$, we conclude. Furthermore, notice that  $\dfrac{h(n)}{h(n+1)}\rightarrow 1$. Calculate
Since the o(1) term and
$\dfrac{h(n)}{h(n+1)}\rightarrow 1$. Calculate
Since the o(1) term and \begin{align*} -\frac{X_{n+1}}{h(n+1)} &= -\frac{X_{n+1}-X_{n} }{h(n+1)} -\frac{X_{n}}{h(n)}\cdot\frac{h(n)}{h(n+1)}\\[4pt]
&\geq o(1)-2\epsilon \frac{h(n)}{h(n+1)}. \end{align*}
\begin{align*} -\frac{X_{n+1}}{h(n+1)} &= -\frac{X_{n+1}-X_{n} }{h(n+1)} -\frac{X_{n}}{h(n)}\cdot\frac{h(n)}{h(n+1)}\\[4pt]
&\geq o(1)-2\epsilon \frac{h(n)}{h(n+1)}. \end{align*}
 $\frac{h(n)}{h(n+1)}$ depend only on n, we conclude Part 2.
$\frac{h(n)}{h(n+1)}$ depend only on n, we conclude Part 2.
-
3. Using the inequality (17) we find that
 $\frac{1-\gamma}{k-1} - \gamma <\frac{-1-\delta}{2}$ for some
$\frac{1-\gamma}{k-1} - \gamma <\frac{-1-\delta}{2}$ for some  $\delta>0$, so
Therefore, by Doob’s inequality we have
$\delta>0$, so
Therefore, by Doob’s inequality we have \begin{equation*} \left(m^{\gamma} h(m+1)\right)^{-1}\sim m^{\frac{1-\gamma}{k-1} - \gamma } \leq m^{\frac{1-\gamma}{k-1} - \gamma }\leq m^{\frac{-1-\delta}{2}} .\end{equation*}
\begin{equation*} \left(m^{\gamma} h(m+1)\right)^{-1}\sim m^{\frac{1-\gamma}{k-1} - \gamma } \leq m^{\frac{1-\gamma}{k-1} - \gamma }\leq m^{\frac{-1-\delta}{2}} .\end{equation*}
 \begin{align*} \mathbb{P}\left(\sup_{u\geq n_0 } ({G'}_u^{n_0} |\mathcal{F}_{n_0})^2 \geq \frac{\epsilon^2}{4}\right) &\leq \sum_{m\geq n_0 } \frac{\mathbb{E}(Y_{m+1}^2|\mathcal{F}_{n_0} ) }{m^{2\gamma} h^2(m+1) }\\[5pt]
&\leq C\sum_{m\geq n_0 } \frac{1 }{m^{2\gamma} h^2(m+1) }\\[5pt]
&=\sum_{m\geq n_0 } \Theta \left(m^{2\left(\frac{1-\gamma}{k-1} - \gamma \right) } \right)\\[5pt]
&=\sum_{m\geq n_0 } \Theta \left(m^{-1-\delta} \right )\\[5pt]
&= \Theta \left({n_0}^{-\delta} \right) \to 0. \end{align*}
\begin{align*} \mathbb{P}\left(\sup_{u\geq n_0 } ({G'}_u^{n_0} |\mathcal{F}_{n_0})^2 \geq \frac{\epsilon^2}{4}\right) &\leq \sum_{m\geq n_0 } \frac{\mathbb{E}(Y_{m+1}^2|\mathcal{F}_{n_0} ) }{m^{2\gamma} h^2(m+1) }\\[5pt]
&\leq C\sum_{m\geq n_0 } \frac{1 }{m^{2\gamma} h^2(m+1) }\\[5pt]
&=\sum_{m\geq n_0 } \Theta \left(m^{2\left(\frac{1-\gamma}{k-1} - \gamma \right) } \right)\\[5pt]
&=\sum_{m\geq n_0 } \Theta \left(m^{-1-\delta} \right )\\[5pt]
&= \Theta \left({n_0}^{-\delta} \right) \to 0. \end{align*}
Notice that the previous claim holds for any stopping time ![]() $ \tau$, in place of n. So we obtain a version of the previous lemma for stopping times.
$ \tau$, in place of n. So we obtain a version of the previous lemma for stopping times.
Lemma 6.5. Let ![]() $\tau$ be a stopping time such that
$\tau$ be a stopping time such that ![]() $\tau \geq n_0$, where
$\tau \geq n_0$, where ![]() $n_0$ is the same as in the previous claim. Then
$n_0$ is the same as in the previous claim. Then ![]() $\mathbb{P} ({G'}_{\tau,n} \in (\frac{-\epsilon}{2}, \frac{\epsilon}{2})\forall n \geq \tau | \mathcal{F}_{\tau} ) >0.$
$\mathbb{P} ({G'}_{\tau,n} \in (\frac{-\epsilon}{2}, \frac{\epsilon}{2})\forall n \geq \tau | \mathcal{F}_{\tau} ) >0.$
Let
 \begin{equation*} \epsilon \leq \min \left( \frac{1}{4}, \frac{1}{2} \left(\frac{1-\gamma}{3(k-1)} \right)^{ \frac{1}{k-1} } \right ) ,\end{equation*}
\begin{equation*} \epsilon \leq \min \left( \frac{1}{4}, \frac{1}{2} \left(\frac{1-\gamma}{3(k-1)} \right)^{ \frac{1}{k-1} } \right ) ,\end{equation*}
and define a stopping time ![]() $\tau=\inf \{n\geq n_0 | Z_n < -2\epsilon \} $.
$\tau=\inf \{n\geq n_0 | Z_n < -2\epsilon \} $.
Proposition 6.2 Let ![]() $(X_n)_{n\geq 1}$ satisfy (35). If
$(X_n)_{n\geq 1}$ satisfy (35). If ![]() $\tau<\infty$ holds with positive probability, then
$\tau<\infty$ holds with positive probability, then ![]() $\mathbb{P}(X_n\to 0 )>0$. More specifically, the process
$\mathbb{P}(X_n\to 0 )>0$. More specifically, the process ![]() $(X_n \,:\, n\geq \tau)$ converges to zero with positive probability.
$(X_n \,:\, n\geq \tau)$ converges to zero with positive probability.
Proof. On the event ![]() $\{X_m<0 \text{for\,all} m\geq n \}$ we use the expression for
$\{X_m<0 \text{for\,all} m\geq n \}$ we use the expression for ![]() $Z_n = -\dfrac{X_n}{h(n)}$ and obtain, as in (31) (except now the inequalities are reversed),
$Z_n = -\dfrac{X_n}{h(n)}$ and obtain, as in (31) (except now the inequalities are reversed),
 \begin{align*} Z_{n+1}-Z_n &\leq \frac{ X_n }{h(n+1) n^\gamma} \left(-a_n \frac{1-\gamma}{ k-1 } |h(n)|^{k-1}-\frac{|X_n|^k }{X_n} \right ) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}\\ &
< \frac{ X_n }{h(n+1) n^\gamma} \left(- \frac{1-\gamma}{ 2(k-1) } |h(n)|^{k-1}-\frac{|X_n|^k }{X_n} \right ) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}. \end{align*}
\begin{align*} Z_{n+1}-Z_n &\leq \frac{ X_n }{h(n+1) n^\gamma} \left(-a_n \frac{1-\gamma}{ k-1 } |h(n)|^{k-1}-\frac{|X_n|^k }{X_n} \right ) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}\\ &
< \frac{ X_n }{h(n+1) n^\gamma} \left(- \frac{1-\gamma}{ 2(k-1) } |h(n)|^{k-1}-\frac{|X_n|^k }{X_n} \right ) -\frac{ Y_{n+1} }{n^\gamma h(n+1)}. \end{align*}
Set
Then we have
 \begin{equation} Z_m - Z_{\tau}\leq \sum_{ i = \tau }^{m-1} D_i + {G'}_{\tau,m}. \end{equation}
\begin{equation} Z_m - Z_{\tau}\leq \sum_{ i = \tau }^{m-1} D_i + {G'}_{\tau,m}. \end{equation}
Now we will show by contradiction that on the event ![]() $A=\{{G'}_{\tau,n} \in (-\frac{\epsilon}{2}, \frac{\epsilon}{2}) \forall n \geq \tau \}$ the process satisfies
$A=\{{G'}_{\tau,n} \in (-\frac{\epsilon}{2}, \frac{\epsilon}{2}) \forall n \geq \tau \}$ the process satisfies ![]() $X_n < 0$ for all
$X_n < 0$ for all ![]() $n \geq \tau$. Define
$n \geq \tau$. Define ![]() $\tau_0 =\inf \{n\geq \tau| Z_n \geq 0 \}$ and
$\tau_0 =\inf \{n\geq \tau| Z_n \geq 0 \}$ and ![]() $\sigma = \sup \{ \tau \leq n <\tau_0 | Z_{n-1}\leq -2\epsilon, \,Z_n>-2\epsilon \} $. Also, when
$\sigma = \sup \{ \tau \leq n <\tau_0 | Z_{n-1}\leq -2\epsilon, \,Z_n>-2\epsilon \} $. Also, when ![]() $Z_n\geq -2\epsilon$ we have
$Z_n\geq -2\epsilon$ we have ![]() $X_n \geq 2\epsilon h(n)= -2\epsilon n^{ \frac{1-\gamma}{1-k}} $. So
$X_n \geq 2\epsilon h(n)= -2\epsilon n^{ \frac{1-\gamma}{1-k}} $. So ![]() $ \frac{|X_n|^k}{ X_n } \geq -(2\epsilon)^{k-1} n^{-1+\gamma } $. Therefore, by the definition of
$ \frac{|X_n|^k}{ X_n } \geq -(2\epsilon)^{k-1} n^{-1+\gamma } $. Therefore, by the definition of ![]() $\epsilon$, we get
$\epsilon$, we get
Hence ![]() $D_n <0$ whenever
$D_n <0$ whenever ![]() $Z_n\geq -2\epsilon$. If
$Z_n\geq -2\epsilon$. If ![]() $\{\tau_0<\infty \}\cap A$ has positive probability, then
$\{\tau_0<\infty \}\cap A$ has positive probability, then ![]() $\{\sigma<\infty \}\cap A$ does also. Thus, on
$\{\sigma<\infty \}\cap A$ does also. Thus, on ![]() $\{\tau_0<\infty \}\cap A$,
$\{\tau_0<\infty \}\cap A$,
 \begin{align*} 0\leq Z_{\tau_0} &= Z_{\tau} + \sum_{ i = \tau }^{\tau_0-1} D_i + {G'}_{\tau,\tau_0} \\ &= Z_{\tau} -Z_{\sigma} +Z_{\sigma} + \sum_{ i = \tau }^{\tau_0-1} D_i + {G'}_{\tau,\tau_0} \\ &=Z_{\sigma}-{G'}_{\tau,\sigma} +{G'}_{\tau,\tau_0}+\sum_{ i = \sigma }^{\tau_0-1} D_i\\ &<-\epsilon +\frac{\epsilon}{2} +\frac{\epsilon}{2} +0=0, \end{align*}
\begin{align*} 0\leq Z_{\tau_0} &= Z_{\tau} + \sum_{ i = \tau }^{\tau_0-1} D_i + {G'}_{\tau,\tau_0} \\ &= Z_{\tau} -Z_{\sigma} +Z_{\sigma} + \sum_{ i = \tau }^{\tau_0-1} D_i + {G'}_{\tau,\tau_0} \\ &=Z_{\sigma}-{G'}_{\tau,\sigma} +{G'}_{\tau,\tau_0}+\sum_{ i = \sigma }^{\tau_0-1} D_i\\ &<-\epsilon +\frac{\epsilon}{2} +\frac{\epsilon}{2} +0=0, \end{align*}
which is a contradiction.
Now we can complete the proof of the proposition. On the event A the process satisfies ![]() $X_n<0$ for all
$X_n<0$ for all ![]() $n>\tau$; therefore
$n>\tau$; therefore ![]() $ \limsup_{ n \rightarrow \infty} X_n \leq 0$ on A. However, by Lemma 2.4 we have
$ \limsup_{ n \rightarrow \infty} X_n \leq 0$ on A. However, by Lemma 2.4 we have ![]() $\limsup_{ n \rightarrow \infty} X_n \geq 0$ a.s. Therefore, on A,
$\limsup_{ n \rightarrow \infty} X_n \geq 0$ a.s. Therefore, on A, ![]() $X_n\rightarrow 0$.
$X_n\rightarrow 0$.
Remark: On A we showed that ![]() $X_n$ converges to zero, since for all
$X_n$ converges to zero, since for all ![]() $n\geq \tau$,
$n\geq \tau$, ![]() $X_n<0$, and the only place to converge is the origin.
$X_n<0$, and the only place to converge is the origin.
Proof of Theorem 1.5. We define ![]() $\tau=\inf \{n\geq n_0| X_n \in (-\epsilon_2,-\epsilon_1 ) \}$, where
$\tau=\inf \{n\geq n_0| X_n \in (-\epsilon_2,-\epsilon_1 ) \}$, where ![]() $n_0$ is the same as in Lemma 6.5, and
$n_0$ is the same as in Lemma 6.5, and ![]() $\tau_e=\inf\{n| X_n\not \in (-3\epsilon, 3\epsilon) \}$. Let
$\tau_e=\inf\{n| X_n\not \in (-3\epsilon, 3\epsilon) \}$. Let ![]() $(X'_n\,:\, n\geq \tau)$ be a process that satisfies (35). Then we couple
$(X'_n\,:\, n\geq \tau)$ be a process that satisfies (35). Then we couple ![]() $(X_n)$ with
$(X_n)$ with ![]() $(X'_n)$ on
$(X'_n)$ on ![]() $\{ \tau <\infty \}$ so that
$\{ \tau <\infty \}$ so that ![]() $\mathbb{P}(X_n = X'_n, \tau \leq n \leq \tau_e | \{ \tau <\infty \} ) =1$. To show that
$\mathbb{P}(X_n = X'_n, \tau \leq n \leq \tau_e | \{ \tau <\infty \} ) =1$. To show that ![]() $X'_n$ converges to zero with positive probability, first we need to verify that the conditions for Proposition 6.2, are met. The only thing we need to check is that
$X'_n$ converges to zero with positive probability, first we need to verify that the conditions for Proposition 6.2, are met. The only thing we need to check is that ![]() $Z'_\tau= - \frac{X'_\tau}{h(\tau)} <-2\epsilon$. However, since
$Z'_\tau= - \frac{X'_\tau}{h(\tau)} <-2\epsilon$. However, since ![]() $h(t)\rightarrow 0$ this is always possible by choosing
$h(t)\rightarrow 0$ this is always possible by choosing ![]() $n_0$ large enough. Furthermore, by Proposition 6.2, we see that there is an event of positive probability such that
$n_0$ large enough. Furthermore, by Proposition 6.2, we see that there is an event of positive probability such that ![]() $X'_n\rightarrow 0$, where
$X'_n\rightarrow 0$, where ![]() $\tau_e$ is infinite conditioned on this event. Therefore,
$\tau_e$ is infinite conditioned on this event. Therefore, ![]() $X_n$ converges to 0 with positive probability.
$X_n$ converges to 0 with positive probability.
Acknowledgements
The author would like to thank Marcus Michelen, Albert Chen, and Josh Rosenberg for constructive criticism of the manuscript.