Article contents
Fixed point sets and the fundamental group I: semi-free actions on G-CW-complexes
Published online by Cambridge University Press: 03 August 2023
Abstract
Smith theory says that the fixed point set of a semi-free action of a group 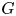 $G$ on a contractible space is
$G$ on a contractible space is 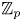 ${\mathbb {Z}}_p$-acyclic for any prime factor
${\mathbb {Z}}_p$-acyclic for any prime factor  $p$ of the order of
$p$ of the order of 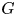 $G$. Jones proved the converse of Smith theory for the case
$G$. Jones proved the converse of Smith theory for the case 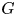 $G$ is a cyclic group acting semi-freely on contractible, finite CW-complexes. We extend the theory to semi-free group actions on finite CW-complexes of given homotopy types, in various settings. In particular, the converse of Smith theory holds if and only if a certain
$G$ is a cyclic group acting semi-freely on contractible, finite CW-complexes. We extend the theory to semi-free group actions on finite CW-complexes of given homotopy types, in various settings. In particular, the converse of Smith theory holds if and only if a certain  $K$-theoretical obstruction vanishes. We also give some examples that show the geometrical effects of different types of
$K$-theoretical obstruction vanishes. We also give some examples that show the geometrical effects of different types of 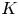 $K$-theoretical obstructions.
$K$-theoretical obstructions.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



