Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-14T11:25:26.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic ill-posedness of the energy–momentum equations and differential inclusions

Part of: Representations of solutions Optimality conditions Calculus of variations and optimal control; optimization

Published online by Cambridge University Press:  26 September 2023

Erik Duse
Erik Duse*
Affiliation:
Department of Mathematics and Statistics, KTH, Stockholm, Sweden (duse@kth.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the energy–momentum equations arising from inner variations whose Lagrangian satisfies a generic symmetry condition are ill-posed. This is done by proving that there exists a subclass of Lipschitz solutions that are also solutions to a differential inclusion into the orthogonal group and in particular these solutions can be nowhere $C^1$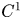. We prove that these solutions are not stationary points if the Lagrangian $W$ 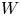is $C^1$ 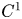and strictly rank-one convex. In view of the Lipschitz regularity result of Iwaniec, Kovalev and Onninen for solution of the energy–momentum equation in dimension 2, we give a sufficient condition for the non-existence of a partial $C^1$ -regularity result even under the condition that the mappings satisfy a positive Jacobian determinant condition. Finally, we consider a number of well-known functionals studied in non-linear elasticity and geometric function theory and show that these do not satisfy this obstruction to partial regularity.

Keywords

calculus of variationsinner variationsenergy–momentum equationsdifferential inclusions

MSC classification

Primary: 49-00: General reference works (handbooks, dictionaries, bibliographies, etc.)
Secondary: 49K99: None of the above, but in this section 35D99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, J.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63 (1978), 337–403.CrossRefGoogle Scholar
Ball, J.. Global invertibility of Sobolev functions and the interpenetration of matter. Proc. R. Soc. Edinburgh 88A (1981), 315–328.CrossRefGoogle Scholar
Ball, J.. Differentiability properties of symmetric and isotropic functions. Duke Math. J. 51 (1984), 00000.CrossRefGoogle Scholar
Ball, J.. Minimisers and the Euler-Lagrange equations. In Trends and applications of pure mathematics to mechanics (eds. P. G. Ciarlet and M. Roseau), pp. 1–4 (Springer, 1984).CrossRefGoogle Scholar
Ball, J.. Some open problems in elasticity. In Geometry, mechanics, and dynamics, pp. 3–59 (New York: Springer, 2002).CrossRefGoogle Scholar
Ball, J. and Murat, F.. $W^1,p$-quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984), 225–253.CrossRefGoogle Scholar
Bauman, P., Owen, N. C. and Phillips, D.. Maximal smoothness of solutions to certain Euler- Lagrange equations from nonlinear elasticity. Proc. R. Soc. Edinburgh A 119 (1991), 241–263.CrossRefGoogle Scholar
Clarke, F. H.. On the inverse function theorem. Pac. J. Math. 64 (1976), 97–102.CrossRefGoogle Scholar
Dacorogna, B.. Direct methods in the calculus of variations, 2nd edn. Applied Mathematical Sciences, vol. 78 (NY: Springer, 2008).Google Scholar
Dacorogna, B., Marcellini, P. and Paolini, E.. Lipschitz-continuous local isometric immersions: rigid maps and origami. J. Math. Pures Appl. 90 (2008), 66–81.CrossRefGoogle Scholar
De Lellis, C., De Philippis, G., Kirchheim, B. and Tione, R.. Geometric measure theory and differential inclusions. Ann. Fac. Sci. Toulouse Math. Ser. 6 30 (2021), 899–960.CrossRefGoogle Scholar
Fusco, N. and Hutchinson, we J.. Partial regularity in problems motivated by nonlinear elasticity. SIAM J. Math. Anal. 22 (1991), 1516–1551.CrossRefGoogle Scholar
Giaquinta, M. and Hildebrandt, S.. Calculus of variations I. Grundlehren Math. Wiss. 310 (2004).CrossRefGoogle Scholar
Giaquinta, M. and Martinazzi, L.. An introduction to the regularity theory for elliptic systems, harmonic maps and minimal graphs, 2nd edn. Lecture Notes 2012 Scuola Normale Superiore Pisa (Pisa, Italy: Springer, 2012).CrossRefGoogle Scholar
Iwaniec, T., Kovalev, L. and Onninen, J.. Lipschitz regularity for inner-variational equations. Duke Math. J. 162 (2013), 643–672.CrossRefGoogle Scholar
Iwaniec, T., Martin, G. and Onninen, J.. Geometric function theory and non-linear analysis. Oxford Mathematical Monographs (Oxford: Oxford University Press, 2001).Google Scholar
Iwaniec, T., Martin, G. and Onninen, J.. Energy-minimal principles in geometric function theory. New Zealand J. Math. 52 (2021), 605–642.CrossRefGoogle Scholar
Iwaniec, T. and Onninen, J.. Mappings of least Dirichlet energy and their HOPF differentials. Arch. Ration. Mech. Anal. 209 (2013), 401–453.CrossRefGoogle Scholar
Iwaniec, T., Verchota, G. C. and Vogel, A. L.. The failure of rank-one connections. Arch. Ration. Mech. Anal. 163 (2002), 125–169.CrossRefGoogle Scholar
Jost, J.. A note on harmonic maps between surfaces. Ann. l'I. H. P. Sect. C 2 (1985), 397–405.Google Scholar
Kristensen, J. and Raita, B.. An introduction to generalized Young measures. Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig, Lecture Note No. 45.Google Scholar
Kristensen, J. and Taheri, A.. Partial regularity of strong local minimizers in the multi-dimensional calculus of variations. Arch. Ration. Mech. Anal. 170 (2003), 63–89.CrossRefGoogle Scholar
Lin, F.-H.. A remark on the map $x/|x|$. C. R. Acad. Sci. Paris Sér. I. Math. 305 (1987), 529–531.Google Scholar
Martin, G. and Yao, C.. Higher regularity and uniqueness for inner variational equations. Calc. Var. 61 (2022), 20.CrossRefGoogle Scholar
Müller, S. and S̆verák, V.. Convex integration with constraints and applications to phase transitions and partial differential equations. J. Eur. Math. Soc. 1 (1999), 393–422.Google Scholar
Müller, S., S̆verák, V.. Convex integration for Lipschitz mappings and counterexamples to regularity. Ann. Math. 157 (2003), 715–742.CrossRefGoogle Scholar
Serre, D.. Symmetric divergence-free tensors in the calculus of variations. C.R. Math. 360 (2022), 653–663.Google Scholar
Sivaloganathan, J. and Spector, S. J.. A construction of infinitely many singular weak solutions to the equations of nonlinear elasticity. Proc. R. Soc. Edinburgh A 132 (2002), 985–992.CrossRefGoogle Scholar
Šverák, V.. Regularity properties of deformations with finite energy. Arch. Ration. Mech. Anal. 100 (1988), 105–127.CrossRefGoogle Scholar
Székelyhidi, L. Jr. From isometric embeddings to turbulence. In HCDTE lecture notes. Part II. Nonlinear hyperbolic PDEs, dispersive and transport equations. AIMS Ser. Appl. Math., vol. 7, p. 63 (MO: AIMS, Springfield, 2013).Google Scholar
Székelyhidi, L. Jr. The regularity of critical points of polyconvex functionals. Arch. Ration. Mech. Anal. 172 (2004), 133–152.CrossRefGoogle Scholar
Taheri, A.. Strong versus weak local minimizers for the perturbed Dirichlet functional. Calc. Var. 15 (2002), 215–235.CrossRefGoogle Scholar
Tione, R.. Minimal graphs and differential inclusions. Commun. Partial Differ. Equ. 46 (2021), 1162–1194.CrossRefGoogle Scholar
Uhlenbeck, K.. Regularity for a class of non-linear elliptic systems. Acta Math. 138 (1977), 219–240.CrossRefGoogle Scholar