In this paper, we show that Leavitt path algebras of weighted graphs and Leavitt path algebras of separated graphs are intimately related. We prove that any Leavitt path algebra 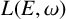 $L(E,\omega )$ of a row-finite vertex weighted graph
$L(E,\omega )$ of a row-finite vertex weighted graph 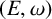 $(E,\omega )$ is
$(E,\omega )$ is  $*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph
$*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph 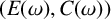 $(E(\omega ),C(\omega ))$. For a general locally finite weighted graph
$(E(\omega ),C(\omega ))$. For a general locally finite weighted graph  $(E, \omega )$, we show that a certain quotient
$(E, \omega )$, we show that a certain quotient 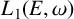 $L_1(E,\omega )$ of
$L_1(E,\omega )$ of 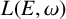 $L(E,\omega )$ is
$L(E,\omega )$ is  $*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph
$*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph 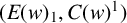 $(E(w)_1,C(w)^1)$. We furthermore introduce the algebra
$(E(w)_1,C(w)^1)$. We furthermore introduce the algebra 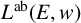 ${L^{\mathrm {ab}}} (E,w)$, which is a universal tame
${L^{\mathrm {ab}}} (E,w)$, which is a universal tame  $*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of
$*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of 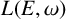 $L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra
$L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra 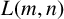 $L(m,n)$.
$L(m,n)$.