We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article, by the use of nth derivative characterization, we obtain several some sufficient conditions for all solutions of the complex linear differential equation to lie in weighted Dirichlet spaces and derivative Hardy spaces, respectively, where 
$$ \begin{align*}f^{(n)}+A_{n-1}(z)f^{(n-1)}+\ldots+A_1(z)f'+A_0(z)f=A_n(z) \end{align*} $$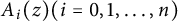
$A_i(z) (i=0,1,\ldots ,n)$ are analytic functions defined in the unit disc. This work continues the lines of the investigations by Heittokangas, et al. for growth estimates about the solutions of the above equation.
We characterize the membership in the Schatten ideals 
$\mathcal {S}_p$, 
$0<p<\infty $, of composition operators acting on weighted Dirichlet spaces. Our results concern a large class of weights. In particular, we examine the case of perturbed superharmonic weights. Characterization of composition operators acting on weighted Bergman spaces to be in 
$\mathcal {S}_p$ is also given.
