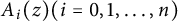1 Introduction
Denote by
$\mathbb {D}$
the open unit disc in the complex plane and by
$\partial \mathbb {D}=\{z:|z|=1\}$
the unit circle. Define
$H(\mathbb {D})$
as the space of all analytic functions on
$\mathbb {D}$
.
In 1982, the complex second-order equation
$$ \begin{align*}f"+A(z)f=0,\end{align*} $$
where
$A(z)\in H(\mathbb {D})$
, was investigated by Pommerenke [Reference Pommerenke37]. By means of Carleson measures, he showed some sufficient conditions on the analytic function
$A(z)$
such that all solutions of the above equation lie in Hardy spaces. Later on, complex linear differential equations of second and even higher orders on the unit disc attracted the attention of many scholars. In
$2000$
, Heittokangas [Reference Heittokangas19] investigated the growth of the solutions of the equation
$$ \begin{align} f^{(n)}+A_{n-1}(z)f^{(n-1)}+\ldots+A_1(z)f'+A_0(z)f=A_n(z) \end{align} $$
where
$n\geq 2$
. He wished to find some sufficient conditions for the coefficients
$A_i(z)(i=0,1,\ldots ,n)$
such that all solutions of the (1.1) lie in some function spaces (i.e., weighted Hardy spaces, Bloch type spaces and general function spaces
$F(p,q,s)$
). In [Reference Huusko, Korhonen and Reijonen25], two sufficient conditions for all solutions of (1.1) to lie in growth spaces
$H^{\infty }_{\alpha }$
were presented by Huusko et al. Recall that for
$0<\alpha <\infty $
,
$H^{\infty }_{\alpha }$
is the space consisting of all functions
$f\in H(\mathbb {D})$
such that
$$ \begin{align*}\|f\|_{H^{\infty}_{\alpha}}:=\sup_{z\in\mathbb{D}}|f(z)|(1-|z|^2)^{\alpha}<\infty.\end{align*} $$
Recently, (1.1) had been extensively studied in some other function spaces, such as weighted Fock spaces [Reference Hu, Huusko, Long and Sun24], Morrey spaces [Reference Sun, Liu and Hu39] and Dirichlet–Morrey spaces [Reference Sun, Liu and Liu40]. In particular, for the case of
$A_n(z)=0$
, a lot of works had been done by a number of researchers. For instance, by means of sharp estimates of logarithmic derivatives, Gundersen–Steinbart–Wang [Reference Gundersen, Steinbart and Wang17] showed that every solution f of the linear differential equation
$$ \begin{align*}f^{(n)}+p_{n-1}(z)f^{(n-1)}+\ldots+p_1(z)f'+p_0(z)f=0 \end{align*} $$
where
$p_i(z)$
are polynomials and
$p_0\neq 0$
, is entire of finite rational order. The related problems in the unit disc were later considered by Chyzhykov et al. [Reference Chyzhykov, Gundersen and Heittokangas5]. Indeed, they investigated the impact of the increasing in coefficients on the growth of solutions of the equation
$$ \begin{align} f^{(n)}+A_{n-1}(z)f^{(n-1)}+\ldots+A_1(z)f'+A_0(z)f=0. \end{align} $$
Later on, Korhonen and Rättyä [Reference Korhonen and Rättyä26] continued the work of Chyzhykov et al. to show a precise estimate for the growth of solutions of the (1.2). In [Reference Heittokangas, Korhonen and Rättyä21], Heittokangas et al. studied the growth relation between the coefficients and the solutions of the (1.2) in weighted Bergman or Hardy spaces. Indeed, they show that when the coefficients in the (1.2) belong to weighted Bergman or Hardy spaces, then all solutions are of some finite orders of growth, measured according to the Nevanlinna characteristic. For more related results, we refer the readers to [Reference Benbourenane and Sons4, Reference Gröhn, Huusko and Rättyä15, Reference Heittokangas, Korhonen and Rättyä20, Reference Li and Li27, Reference Li and Wulan28, Reference Xiao42].
In this article, motivated by the above works, we are interested in studying the sufficient conditions for all solutions of the (1.1) to lie in derivative Hardy spaces and weighted Dirichlet spaces. Now, let’s recall their definitions.
Definition 1.1. Let
$0<p<\infty $
. The derivative Hardy space
$S^p$
is a proper subspace of Hardy space
$H^2$
and consists of
$f\in H(\mathbb {D})$
satisfying
$$ \begin{align*}\|f\|_{S^p}:=\left(|f(0)|^p+\|f'\|_{H^p}\right)^{1/p}=\left(|f(0)|^p+\sup_{0<r<1}\frac{1}{2\pi}\int^{2\pi}_{0}|f'(re^{i\theta})|^pd\theta\right)^{1/p}<\infty.\end{align*} $$
In particular, for any
$f(z)=\sum ^{\infty }_{n=0}a_nz^n\in H(\mathbb {D})$
, it holds that
$\|f\|^2_{S^2}=|f(0)|^2+\sum _{n=1}^{\infty }n^2|a_n|^2$
. In 1978, Roan [Reference Roan38] started on the investigations for the boundedness of composition operators on derivative Hardy spaces. Related problems were also investigated by MacCluer [Reference MacCluer35]. After their works, Contreras and Hernández–Díaz [Reference Contreras and Hernández-Díaz6] made a systematic work on the boundedness, compactness, complete continuity, and weak compactness of weighted composition operators on derivative Hardy spaces. Recently, Lin, et al. [Reference Lin, Liu and Wu32] showed the boundedness of Volterra type operators on derivative Hardy spaces. Other intriguing issues about derivative Hardy spaces have been studied, including linear isometries [Reference Novinger and Oberlin36], invariant subspace problems [Reference Čučković and Paudyal7, Reference Čučković and Paudyal8, Reference Lin29, Reference Lin, Liu and Wu32], order boundedness of weighted composition operators [Reference Lin31, Reference Lin, Liu and Wu33] and so forth. For more results about the derivative Hardy spaces, we refer the readers to [Reference Allen, Heller and Pons2, Reference Duren9, Reference Gu and Luo16, Reference Gupta and Gupta18, Reference Heller22, Reference Heller23] and the references therein.
For
$0<p<\infty $
and
$-1<\alpha <\infty $
, the weighted Bergman space
$A^p_{\alpha }$
consists of all
$f\in H(\mathbb {D})$
such that
$$ \begin{align*}\|f\|^p_{A^p_{\alpha}}:=\int_{\mathbb{D}}|f(w)|^pdA_{\alpha}(w)<\infty\end{align*} $$
where
$dA(w)=(1/\pi )dxdy$
is the normalized Lebesgue area measure on
$\mathbb {D}$
and
$dA_{\alpha }(w)=(1+\alpha )(1-|w|^2)^{\alpha }dA(w)$
is the weighted Lebesgue measure (See [Reference Duren and Schuster10] or [Reference Zhu43] for more information about Bergman spaces).
Definition 1.2. For
$0<p<\infty $
and
$-1<\alpha <\infty $
, the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
consists of all
$f\in H(\mathbb {D})$
such that
$$ \begin{align*}\|f\|_{\mathcal{D}^p_{\alpha}}:=\left(|f(0)|^p+\int_{\mathbb{D}}|f'(w)|^pdA_{\alpha}(w) \right) ^{1/p}<\infty.\end{align*} $$
It is obvious that for any
$f\in H(\mathbb {D})$
,
$f\in \mathcal {D}^p_{\alpha }$
if and only if
$f'\in A^p_{\alpha }$
. When
$p<\alpha +1$
, the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
coincides with the weighted Bergman space
$A^{p}_{\alpha -p}$
with equivalent norms. If
$p>\alpha +2$
, the weighted Dirichlet space
$\mathcal {D}^p_{\alpha }$
is contained in the essentially bounded space
$H^{\infty }$
(see [Reference Wu41, Theorem 4.2]).
In 1999, Wu [Reference Wu41] gave the Carleson measure characterization for the weighted Dirichlet space
$\mathcal {D}^{p}_{\alpha }$
when
$p\geq \alpha +1$
. In addition, he provided a sufficient and necessary condition, in terms of Carleson measures, for boundedness of multiplication operators on such weighted Dirichlet spaces. Related studies also appeared in the work of Arcozzi–Rochberg–Sawyer [Reference Arcozzi, Rochberg and Sawyer3]. Continuing their researches, Girela and Peláez [Reference Girela and Peláez12] obtained complete characterizations, in terms of Carleson measures, of conditions that enable the weighted Dirichlet spaces
$\mathcal {D}^{p}_{\alpha }$
to be embedded into the Lebesgue spaces
$L^q(d\mu )$
for
$q>p>0$
, where
$d\mu $
is a positive Borel measure on
$\mathbb {D}$
. Later, the characterizations of boundedness and compactness of multiplication operators and some integration operators on weighted Dirichlet spaces were obtained in [Reference Galanopoulos, Girela and Peláez11, Reference Lin30]. See [Reference Girela and Peláez13] and [Reference Girela and Peláez14] for related studies about weighted Dirichlet spaces.
Now, we state our main results. Theorems 1.1 and 1.2 show two sufficient conditions for all solutions of the (1.1) to lie in weighted Dirichlet spaces. Theorems 1.3 and 1.4 show two sufficient conditions for all solutions of the (1.1) to lie in derivative Hardy spaces.
Theorem 1.1. Let
$0< p<\infty $
and
$\alpha>-1$
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}C_1:=\int_{\mathbb{D}}\left| \int_{0}^{z}\int_{0}^{\xi_1}\ldots\int_{0}^{\xi_{n-2}}A_{n}(\xi_{n-1})d\xi_{n-1}\ldots d\xi_{1}\right| ^pdA_{\alpha}(z)<\infty,\qquad\qquad \end{align*} $$
$$ \begin{align*}C_2:=\int_{\mathbb{D}}\left( \sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \frac{\left| \sum^{m}_{k=1}A^{(m-k)}_{n-k}(\xi_{m})\right|}{(1-|\xi_m|^2)^{\frac{\alpha+2}{p}}} d\xi_m\ldots d\xi_1\right)^pdA_{\alpha}(z)\end{align*} $$
and
$$ \begin{align*}C_3:=\left \{ \begin{array}{ll} \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\frac{\left| A_0(\xi_{n-1})\right|}{(1-|\xi_{n-1}|^2)^{\frac{\alpha+2-p}{p}}} d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z), & \\\quad \text{if}~p<\alpha+2;\\ \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| A_0(\xi_{n-1})\right|\left( \log\frac{2}{1-|\xi_{n-1}|^2}\right) ^{\frac{p-1}{p}} d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z), & \\ \quad \text{if}~p=\alpha+2;\\ \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| A_0(\xi_{n-1})\right| d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z), & \\ \quad \text{if}~p>\alpha+2. \end{array} \right. \end{align*} $$
are two positive constants satisfying
$C_2+C_3<1/d$
, where
$d>0$
is sufficiently large and is only related to
$n,p$
. Then all solutions of the (1.1) lie in
$\mathcal {D}^{p}_{\alpha }$
.
Theorem 1.2. Let
$0< p<\infty $
and
$\alpha>-1$
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}K_1:=\int_{\mathbb{D}}|A_{n}(z)|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)<\infty,\end{align*} $$
$$ \begin{align*} \begin{split} K_2:= \left \{ \begin{array}{ll} \int_{\mathbb{D}}|A_{0}(z)|^p(1-|z|^2)^{pn-\alpha-2}dA_{\alpha}(z), & \text{if}~p<\alpha+2;\\ \int_{\mathbb{D}}|A_{0}(z)|^p(1-|z|^2)^{pn-p}\left( \log\frac{2}{1-|z|^2}\right)^{p-1} dA_{\alpha}(z), & \text{if}~p=\alpha+2;\\ \int_{\mathbb{D}}|A_{0}(z)|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z), & \text{if}~p>\alpha+2, \end{array} \right. \end{split} \end{align*} $$
and
$$ \begin{align*}K_3:=\sum_{i=1}^{n-1} \|A_i\|^p_{H^{\infty}_{n-i}}\end{align*} $$
are two positive constants satisfying
$K_2+K_3<1/c$
, where
$c>0$
is sufficiently large and is only related to
$n,p$
. Then all solutions of the (1.1) lie in
$\mathcal {D}^{p}_{\alpha }$
.
Theorem 1.3. Let
$0< p<\infty $
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}C_1:=\sup_{0<r<1}\frac{1}{2\pi}\int_{0}^{2\pi}\left| \int_{0}^{re^{i\theta }}\int_{0}^{\xi_1}\ldots\int_{0}^{\xi_{n-2}}A_{n}(\xi_{n-1})d\xi_{n-1}\ldots d\xi_{1}\right| ^pd\theta<\infty, \qquad\qquad \end{align*} $$
$$ \begin{align*} C_2:=\sup_{0<r<1}\frac{1}{2\pi}\int_{0}^{2\pi}\left( \sum^{n-1}_{m=1} \int^{re^{i\theta}}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \frac{\left| \sum^{m}_{k=1}A^{(m-k)}_{n-k}(\xi_{m})\right|}{(1-|\xi_m|^2)^{1/p}} d\xi_m\ldots d\xi_1\right)^pd\theta \end{align*} $$
and
$$ \begin{align*}C_3:=\left \{ \begin{array}{ll} \sup_{0<r<1}\frac{1}{2\pi}\int_{0}^{2\pi} \left(\int^{re^{i\theta}}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\frac{\left| A_0(\xi_{n-1})\right|}{(1-|\xi_{n-1}|^2)^{\frac{1-p}{p}}} d\xi_{n-1}\ldots d\xi_1\right)^pd\theta, & \\ \quad \text{if}~0<p<1;\\ \sup_{0<r<1}\frac{1}{2\pi}\int_{0}^{2\pi} \left(\int^{re^{i\theta}}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| A_0(\xi_{n-1})\right|^p d\xi_{n-1}\ldots d\xi_1\right)d\theta , & \\\quad \text{if}~1\leq p<\infty. \end{array} \right. \end{align*} $$
are two positive constants satisfying
$C_2+C_3<1/d$
, where
$d>0$
is sufficiently large and is only related to
$n,p$
. Then all solutions of the (1.1) lie in
$S^{p}$
.
Theorem 1.4. Let
$0< p<\infty $
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}K_1:=\int_{\partial\mathbb{D}}\left(\int_{S(\xi)}|A_{n}(z)|^2(1-|z|^2)^{2n-4}dA(z)\right) ^{p/2}dm(\xi)<\infty,\end{align*} $$
$$ \begin{align*} \begin{split} K_2:= \left \{ \begin{array}{ll} \int_{\partial\mathbb{D}}\left(\int_{S(\xi)}|A_{0}(z)|^2(1-|z|^2)^{2(n-1-\frac{1}{p})}dA(z)\right) ^{p/2}dm(\xi), & \text{if}~0<p<1;\\ \int_{\partial\mathbb{D}}\left(\int_{S(\xi)}|A_{0}(z)|^2(1-|z|^2)^{2n-4}dA(z)\right) ^{p/2}dm(\xi) , & \text{if}~1\leq p<\infty, \end{array} \right. \end{split} \end{align*} $$
and
$$ \begin{align*}K_3:=\sum_{i=1}^{n-1}\min\left\lbrace \|A_i\|^p_{H^{\infty}_{n-i}},\int_{\partial\mathbb{D}}\left(\int_{S(\xi)}|A_{i}(z)|^2(1-|z|^2)^{2(n-j-1-\frac{1}{p})}dA(z)\right) ^{p/2}dm(\xi)\right\rbrace\end{align*} $$
are two positive constants satisfying
$K_2+K_3<1/c$
, where
$c>0$
is sufficiently large and is only related to
$n,p$
. Then all solutions of the (1.1) lie in
$S^{p}$
.
The structure of this article is organized as follows.
In Section 2, we collect some preliminary lemmas that will be used throughout the article. In Section 3, we prove our main results.
Throughout this article, for any two positive functions
$f(x)$
and
$g(x)$
, we write
$f\lesssim g$
if
$f\leq cg$
holds, where c is a positive constant independent of the variable x. We write
$f\approx g$
whenever
$f\lesssim g\lesssim f$
. Moreover, the value of “c” may vary from line to line but will remain independent of the main variables.
2 Preliminaries
First, we need the following two lemmas, which will be used frequently later.
Lemma 2.1. [Reference Duren9]
Suppose that N is a positive integer and
$b_n\geq 0$
for
$n=1,2,\ldots ,N$
. Then
$$ \begin{align*}\left( \sum^{N}_{n=1}b_n\right)^p\leq\sum^{N}_{n=1}b_n^p ,\; 0<p \leq1\end{align*} $$
and
$$ \begin{align*}\left( \sum^{N}_{n=1}b_n\right)^p\leq N^{p-1}\left( \sum^{N}_{n=1}b_n^p\right),\, 1\leq p<\infty .\end{align*} $$
Lemma 2.2. [Reference Zhu43, Theorem 4.28]
Suppose
$p>0$
,
$\alpha>-1$
,
$n\geq 0$
, and
$f\in H(\mathbb {D})$
. Then
$$ \begin{align*}\|f\|_{A^{p}_{\alpha}}\approx\sum^{n-1}_{i=0}|f^{(i)}(0)|^{p}+\int_{\mathbb{D}}|f^{(n)}(z)|^p(1-|z|^2)^{np}dA_{\alpha}(z). \end{align*} $$
Moreover, we need to use the following equivalent norms of
$H^p$
:
Lemma 2.3. [Reference Ahern and Bruna1, p. 125]
Suppose
$0<p<\infty $
and
$f\in H^p$
. Then
$$ \begin{align*}\|f\|^p_{H^p}\approx\sum^{n-1}_{i=0}|f^{(i)}(0)|^p+\int_{\partial\mathbb{D}}\left(\int_{S(\xi)}|f^{(n)}(z)|^2(1-|z|^2)^{2n-2}dA(z) \right)^{p/2}dm(\xi).\end{align*} $$
Next, the growth estimates of elements in
$S^p$
and
$\mathcal {D}^p_{\alpha }$
are given in the following two lemmas, respectively.
Lemma 2.4. (see [Reference Lin, Liu and Wu32, Reference Lin, Liu and Wu33])
If
$1\leq p<\infty $
, then for any
$f\in S^p$
, it holds that
$|f(z)|\leq \pi \|f\|_{S^p}, ~z\in \mathbb {D}.$
If
$0<p<1$
, then for any
$f\in S^p$
,
$$ \begin{align*}|f(z)|\lesssim\frac{\|f\|_{S^p}}{(1-|z|^2)^{1/p-1}},\quad\forall z\in\mathbb{D}.\end{align*} $$
Lemma 2.5. [Reference Wu41]
Let
$0<p< \infty $
and
$\alpha>-1$
. If
$f\in \mathcal {D}^p_{\alpha }$
, then
-
(1)
$|f(z)|\lesssim \frac {\|f\|_{\mathcal {D}^p_{\alpha }}}{(1-|z|^2)^{\frac {\alpha +2-p}{p}}}$
, whenever
$p<\alpha +2;$
-
(2)
$|f(z)|\lesssim \left ( \log \frac {2}{1-|z|^2}\right ) ^{\frac {p-1}{p}}\|f\|_{\mathcal {D}^p_{\alpha }}$
, whenever
$p=\alpha +2 ;$
-
(3)
$|f(z)|\leq \|f\|_{\mathcal {D}^p_{\alpha }}$
, whenever
$p>\alpha +2$
.
In addition, we have to use the following growth estimates for the n-th order derivative function.
Lemma 2.6. Let
$0<p< \infty $
,
$\alpha>-1$
and n be a positive integer. If
$f\in \mathcal {D}^p_{\alpha }$
, then
$$ \begin{align*}|f^{(n)}(z)|\lesssim\frac{\|f\|_{\mathcal{D}^p_{\alpha}}}{(1-|z|^2)^{\frac{2+\alpha}{p}+n-1}},\quad z\in\mathbb{D}.\end{align*} $$
Proof. For any
$z\in \mathbb {D}$
, by [Reference Luecking34, Lemma 2.1], we know
$$ \begin{align*}|f^{(n-1)}(z)|^p\lesssim\frac{\int_{D_r(z)}|f(w)|^pdA_{\alpha}(w)}{(1-|z|^2)^{2+\alpha+(n-1)p}}\lesssim\frac{\int_{\mathbb{D}}|f(w)|^pdA_{\alpha}(w)}{(1-|z|^2)^{2+\alpha+(n-1)p}}.\end{align*} $$
Letting
$f=g'$
yields
$$ \begin{align*}|g^{(n)}(z)|^p\lesssim\frac{\int_{\mathbb{D}}|g'(w)|^pdA_{\alpha}(w)}{(1-|z|^2)^{2+\alpha+(n-1)p}},\end{align*} $$
which is the desired result.
By Lemma 2.3, it is not difficult to obtain the following result.
Lemma 2.7. Let
$0<p<\infty $
and n be a non-negative integer. If
$f\in S^p$
, then
$$ \begin{align*}|f^{(n)}(z)|\lesssim\frac{\|f\|_{S^p}}{(1-|z|^2)^{1/p+n-1}},\quad z\in \mathbb{D}.\end{align*} $$
3 The proof of the main results
Proof of Theorem 1.1
Assume that f is a solution of (1.1), then
$$ \begin{align} f^{(n)}_r(z)+\sum^{n-1}_{j=0}B_{j}(z)f^{(j)}_r(z)=B_n(z),\, z\in\mathbb{D}, \end{align} $$
where
$f_r(z)=f(rz)$
,
$B_j(z)=B_j(z,r)=r^{n-j}A_j(rz)$
,
$j=0,\ldots ,n-1$
,
$B_n(z)=r^nA_n(rz)$
,
$0\leq r<1$
.
By using the equation
$$ \begin{align*} f(z)=\int^{z}_{0}f'(\xi)d\xi+f(0) \end{align*} $$
$n-1$
times, we get
$$ \begin{align*} f'_r(z) &=\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0f_{r}^{(n)}(\xi_{n-1})d\xi_{n-1}\ldots d\xi_1+\sum^{n-2}_{j=0}\frac{f_r^{(j+1)}(0)}{j!}z^j\\ &=\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left(B_n(\xi_{n-1})-\sum^{n-1}_{j=0}B_j(\xi_{n-1})f^{(j)}_r(\xi_{n-1}) \right) d\xi_{n-1}\ldots d\xi_1 \\ &\quad +\sum^{n-2}_{j=0}\frac{f_r^{(j+1)}(0)}{j!}z^j. \end{align*} $$
Combining this with Lemma 2.1, we obtain
$$ \begin{align*} \|f_r\|^p_{\mathcal{D}^p_{\alpha}}&= \int_{\mathbb{D}}|f'_r(z)|^pdA_{\alpha}(z)+|f_r(0)|^p\\ &=\int_{\mathbb{D}}\bigg| \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left(B_n(\xi_{n-1})-\sum^{n-1}_{j=0}B_j(\xi_{n-1})f^{(j)}_r(\xi_{n-1}) \right) d\xi_{n-1}\ldots d\xi_1\\ &\quad +\sum^{n-2}_{j=0}\frac{f_r^{(j+1)}(0)}{j!}z^j\bigg| ^pdA_{\alpha}(z)+|f_r(0)|^p\\ & \lesssim \int_{\mathbb{D}} \left|\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0B_n(\xi_{n-1}) d\xi_{n-1}\ldots d\xi_1\right|^p dA_{\alpha}(z)\\ &\quad +\int_{\mathbb{D}} \left|\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\sum^{n-1}_{j=1}B_j(\xi_{n-1})f_r^{(j)}(\xi_{n-1}) d\xi_{n-1}\ldots d\xi_1\right|^pdA_{\alpha}(z)\\ &\quad +\int_{\mathbb{D}} \left|\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0B_0(\xi_{n-1})f_r(\xi_{n-1}) d\xi_{n-1}\ldots d\xi_1\right|^pdA_{\alpha}(z)\\ &\quad +\int_{\mathbb{D}}\left| \sum^{n-2}_{j=0}\frac{f_r^{(j+1)}(0)}{j!}z^j\right| ^pdA_{\alpha}(z)+|f_r(0)|^p\\ &=I_1+I_2+I_3+I_4+I_5. \end{align*} $$
Let us first discuss
$I_2$
. From [Reference Huusko, Korhonen and Reijonen25, Lemma 12], we have
$$ \begin{align*} I_2 &=\int_{\mathbb{D}} \left|\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\sum^{n-1}_{j=1}\sum^{j-1}_{i=0}(-1)^i \binom{j-1}{i}(f'_r\cdotp B_j^{(i)})^{(j-i-1)}(\xi_{n-1}) d\xi_{n-1}\ldots d\xi_1\right|^p\\ &\quad \times dA_{\alpha}(z) \end{align*} $$
As
$$ \begin{align*} &\int^{\xi_{n-1-(j-i-1)}}_{0}\int^{\xi_{n-(j-i-1)}}_{0}\ldots\int^{\xi_{n-2}}_{0}\left(f'_r\cdotp B_j^{(i)} \right)^{(j-i-1)}(\xi_{n-1})d\xi_{n-1}\ldots d_{n-(j-i-1)}\\ &=\int^{\xi_{n-1-(j-i-1)}}_{0}\int^{\xi_{n-(j-i-1)}}_{0}\ldots\int^{\xi_{n-3}}_{0}\left[ \left(f'_r\cdotp B_j^{(i)} \right)^{(j-i-2)}(\xi_{n-2})-\left(f'_r\cdotp B_j^{(i)} \right)^{(j-i-2)}(0)\right]\\ &\quad \times d\xi_{n-2}\ldots d_{n-(j-i-1)} \\ &=B^{(i)}_j(\xi_{n-1-(j-i-1)})f'_r(\xi_{n-1-(j-i-1)})-\sum^{j-i-2}_{t=0}\frac{\left(B_{j}^{(i)}f'_r \right)^{(t)}(0) }{t!}\xi^{t}_{n-1-(j-i-1)}, \end{align*} $$
then
$$ \begin{align*} I_2&=\int_{\mathbb{D}} \Bigg|\sum^{n-1}_{j=1}\sum^{j-1}_{i=0}(-1)^i \binom{j-1}{i} \\ & \quad \times\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2-(j-i-1)}}_0\Bigg[B^{(i)}_j(\xi_{n-1-(j-i-1)})f'_r(\xi_{n-1-(j-i-1)})\\ &\quad -\sum^{j-i-2}_{t=0}\frac{\left(B_{j}^{(i)}f'_r \right)^{(t)}(0) }{t!}\xi^{t}_{n-1-(j-i-1)}\Bigg] d\xi_{n-1-(j-i-1)}\ldots d\xi_1\Bigg|^pdA_{\alpha}(z). \end{align*} $$
We relabel the indices as follows:
$$ \begin{align*}j=n-k,~i=m-k.\end{align*} $$
It follows that
$$ \begin{align*} I_2=&\int_{\mathbb{D}} \Bigg|\sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \left[ \sum^{m}_{k=1}(-1)^{m-k} \binom{n-k-1}{m-k}B^{(m-k)}_{n-k}(\xi_{m})\right] \\ & \times f'_r(\xi_{m})d\xi_m\ldots d\xi_1-\sum^{n-1}_{j=1}\sum^{j-1}_{i=0}\sum^{j-i-2}_{t=0}(-1)^{i}\binom{j-1}{i}\frac{\left(B_{j}^{(i)}f'_r \right)^{(t)}(0) }{(n-j+i+t)!}z^{n-j+i+t}\Bigg|^pdA_{\alpha}(z)\\ \lesssim&\int_{\mathbb{D}} \left| \sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \left[ \sum^{m}_{k=1}B^{(m-k)}_{n-k}(\xi_{m})\right] f'_r(\xi_{m})d\xi_m\ldots d\xi_1\right|^pdA_{\alpha}(z)\\ ~&+\int_{\mathbb{D}} \left| \sum^{n-1}_{j=1}\sum^{j-1}_{i=0}\sum^{j-i-2}_{t=0}\frac{\left(B_{j}^{(i)}f'_r \right)^{(t)}(0) }{(n-j+i+t)!}z^{n-j+i+t}\right| ^pdA_{\alpha}(z)\\ =&I_{21}+I_{22}. \end{align*} $$
By Lemma 2.6, we have
$$ \begin{align*} I_{21}\leq&\int_{\mathbb{D}}\left( \sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \left| \sum^{m}_{k=1}B^{(m-k)}_{n-k}(\xi_{m})\right| \left| f'_r(\xi_{m})\right|d\xi_m\ldots d\xi_1\right)^pdA_{\alpha}(z)\\ \lesssim&\|f_r\|^{p}_{\mathcal{D}^{p}_{\alpha}}\int_{\mathbb{D}}\left( \sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \frac{\left| \sum^{m}_{k=1}B^{(m-k)}_{n-k}(\xi_{m})\right|}{(1-|\xi_m|^2)^{\frac{\alpha+2}{p}}} d\xi_m\ldots d\xi_1\right)^pdA_{\alpha}(z)\\ \lesssim&\|f_r\|^{p}_{\mathcal{D}^{p}_{\alpha}}C_2. \end{align*} $$
On the other hand, we have
$$ \begin{align*}I_4+I_{22} &= \sup_{z\in\mathbb{D}}\left( \left| \sum^{n-2}_{j=0}\frac{f_r^{(j+1)}(0)}{j!}z^j\right|^p+ \left| \sum^{n-1}_{j=1}\sum^{j-1}_{i=0}\sum^{j-i-2}_{t=0}\frac{\left(B_{j}^{(i)}f'_r \right)^{(t)}(0) }{(n-j+i+t)!}z^{n-j+i+t}\right| ^p\right)\\ & \leq C_f<\infty.\end{align*} $$
Using Lemma 2.5 again, we have
$$ \begin{align*} I_3 &\lesssim\int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| B_0(\xi_{n-1})\right| \left| f_r(\xi_{n-1})\right| d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z) \\ &\lesssim\|f_r\|^{p}_{\mathcal{D}^{p}_{\alpha}}C_3, \end{align*} $$
where
$$ \begin{align*} \begin{split} C_3=\left \{ \begin{array}{ll} \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\frac{\left| B_0(\xi_{n-1})\right|}{(1-|\xi_{n-1}|^2)^{\frac{\alpha+2-p}{p}}} d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z), & \\ \quad\text{if}~p<\alpha+2;\\ \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| B_0(\xi_{n-1})\right|\left( \log\frac{2}{1-|\xi_{n-1}|^2}\right) ^{\frac{p-1}{p}} d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z), & \\ \quad\text{if}~p=\alpha+2;\\ \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\left| B_0(\xi_{n-1})\right| d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z) & \\ \quad\text{if}~p>\alpha+2. \end{array} \right. \end{split} \end{align*} $$
Consequently,
$$ \begin{align*}\|f_r\|_{\mathcal{D}^p_{\alpha}}^{p}\lesssim\frac{C_1+I_{22}+I_4+I_5}{1-d(C_2+C_3)}<\infty,\end{align*} $$
which gives that
$f\in \mathcal {D}^p_{\alpha }$
as
$r\rightarrow 1^{-}$
. This completes the proof.
Proof of Theorem 1.2
Assume that f is a solution of (1.1), then we have
$$ \begin{align*}f^{(n)}_r(z)+\sum^{n-1}_{j=0}B_{j}(z)f^{(j)}_r(z)=B_n(z),\, z\in\mathbb{D},\end{align*} $$
where
$f_r(z)=f(rz)$
,
$B_j(z)=B_j(z,r)=r^{n-j}A_j(rz)$
,
$j=0,\ldots ,n-1$
,
$B_n(z)=r^nA_n(rz)$
,
$0\leq r<1$
.
By Lemmas 2.1 and 2.2, we have
$$ \begin{align*} \|f_r\|^p_{\mathcal{D}^{p}_{\alpha}}\approx&\int_{\mathbb{D}}|f_r^{(n)}(z)|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)+\sum^{n-1}_{k=0}|f^{(k)}_{r}(0)|^p\\ =&\int_{\mathbb{D}}\left|B_n(z)-\sum^{n-1}_{j=0}B_j(z)f_r^{(j)}(z)\right|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)+\sum^{n-1}_{k=0}|f^{(k)}_{r}(0)|^p\\ \leq& \int_{\mathbb{D}}\left(|B_n(z)|+|B_0(z)f_r(z)|+\sum^{n-1}_{j=1}|B_j(z)f_r^{(j)}(z)|\right)^p(1-|z|^2)^{pn-p}dA_{\alpha}(z) \\ &\quad +\,\sum^{n-1}_{k=0}|f^{(k)}_{r}(0)|^p\\ \lesssim& \int_{\mathbb{D}}\left|B_n(z)\right|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)+\int_{\mathbb{D}}\left|B_0(z)f_r(z)\right|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)\\ &~\,+\sum^{n-1}_{j=1}\int_{\mathbb{D}}\left|B_j(z)f_r^{(j)}(z)\right|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)+\sum^{n-1}_{k=0}|f^{(k)}_{r}(0)|^p\\ &=I_1+I_2+I_3+I_4. \end{align*} $$
Applying Lemma 2.5 leads to
$$ \begin{align*} \begin{split} I_2\lesssim \left \{ \begin{array}{ll} \|f_r\|^p_{\mathcal{D}^p_{\alpha}} \int_{\mathbb{D}}|B_{0}(z)|^p(1-|z|^2)^{pn-\alpha-2}dA_{\alpha}(z), & \text{if}~p<\alpha+2;\\ \|f_r\|^p_{\mathcal{D}^p_{\alpha}}\int_{\mathbb{D}}|B_{0}(z)|^p(1-|z|^2)^{pn-p}\left( \log\frac{2}{1-|z|^2}\right)^{p-1} dA_{\alpha}(z), & \text{if}~p=\alpha+2;\\ \|f_r\|^p_{\mathcal{D}^p_{\alpha}}\int_{\mathbb{D}}|B_{0}(z)|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z) & \text{if}~p>\alpha+2. \end{array} \right. \end{split} \end{align*} $$
On the other hand,
$$ \begin{align*} I_3\leq& \sum^{n-1}_{j=1}\left(\sup_{z\in\mathbb{D}}|B_{j}(z)|^p(1-|z|^2)^{p(n-j)}\right) \int_{\mathbb{D}}\left|f_r^{(j)}(z)\right|^p(1-|z|^2)^{pj-p}dA_{\alpha}(z)\\ \leq&\sum^{n-1}_{j=1}\|B_j\|^p_{H^{\infty}_{n-j}}\|f_r\|^p_{\mathcal{D}^p_{\alpha}}. \end{align*} $$
Consequently,
$I_3\lesssim K_3\|f_r\|^p_{\mathcal {D}^p_{\alpha }}$
. It follows from the assumption that
$$ \begin{align*}\|f_r\|^p_{\mathcal{D}^p_{\alpha}}\lesssim\frac{K_1+I_4}{1-c(K_2+K_3)}<\infty,\end{align*} $$
for
$0\leq r<1$
. Letting
$r\rightarrow 1^{-}$
gives that
$f\in \mathcal {D}^p_{\alpha }$
. This completes the proof.
Remark 3.1. Although the sufficient condition in Theorems 1.1 and 1.2 is more complicated, in fact, we can illustrate the feasibility of that sufficient condition by some examples. Let us consider the complex second-order equation
$$ \begin{align*}f"+A(z)f=0.\end{align*} $$
Fix a constant-valued function
$A(z)=k(k\in \mathbb {R})$
satisfying the condition
$$ \begin{align*}\int_{\mathbb{D}}|A_0(z)|^p(1-|z|^2)pdA_{\alpha}(z)<\frac{1}{c}.\end{align*} $$
If
$k<0$
, we can easily find that the solution to the equation
$f"+kf=0$
has a solution base
$\{f_1,f_2\}$
, where
$$ \begin{align*}f_1(z)=e^{\sqrt{-k}z} ~\text{and }~ f_2(z)=e^{-\sqrt{-k}z}. \end{align*} $$
If
$k>0$
, then the equation
$f"+kf=0$
has a solution base
$\{f_1,f_2\}$
, where
$$ \begin{align*}f_3(z)=\cos(kz) ~\text{and }~ f_4(z)=\sin(kz).\end{align*} $$
It can be seen that
$f_1,f_2,f_3$
and
$f_4$
belongs to the weighted Dirichlet spaces
$\mathcal {D}^{p}_{\alpha }(p>\alpha +2)$
.
On the other hand, if we consider the equation
$f^{(n)}=0$
, then it is easy to know that all solutions of this equation are
$$ \begin{align*}f(z)=a_0+a_1z+a_2z^2+a_3z^3+\ldots+a_{n-1}z^{n-1}.\end{align*} $$
Obviously,
$f\in \mathcal {D}^{p}_{\alpha }$
.
Proof of Theorem 1.3
The proof can be accomplished by using Lemmas 2.1, 2.4, and 2.7, and the similar proof of Theorem 1.1.
Proof of Theorem 1.4
The proof can be accomplished by using Lemmas 2.3, 2.4 and 2.7, and the similar proof of Theorem 1.2.
The following two corollaries provide some stronger sufficient conditions making the solutions of the 1.1 lie in weighted Dirichlet spaces.
The first one is a variant of Theorem 1.1.
Corollary 3.2. Let
$0< p<\infty $
and
$\alpha>-1$
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}C_1:=\int_{\mathbb{D}}\left| \int_{0}^{z}\int_{0}^{\xi_1}\ldots\int_{0}^{\xi_{n-2}}A_{n}(\xi_{n-1})d\xi_{n-1}\ldots d\xi_{1}\right| ^pdA_{\alpha}(z)<\infty,\qquad\quad \end{align*} $$
$$ \begin{align*}C_2:=\int_{\mathbb{D}}\left( \sum^{n-1}_{m=1} \int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{m-1}}_0 \frac{\left| \sum^{m}_{k=1}A^{(m-k)}_{n-k}(\xi_{m})\right|}{(1-|\xi_m|^2)^{\frac{\alpha+2}{p}}} d\xi_m\ldots d\xi_1\right)^pdA_{\alpha}(z),\end{align*} $$
and
$$ \begin{align*}O_3:= \int_{\mathbb{D}} \left(\int^{z}_0\int^{\xi_1}_0\ldots\int^{\xi_{n-2}}_0\frac{\left| A_0(\xi_{n-1})\right|}{(1-|\xi_{n-1}|^2)^{\frac{\alpha+2+p}{p}}} d\xi_{n-1}\ldots d\xi_1\right)^pdA_{\alpha}(z)\end{align*} $$
are two positive constants satisfying
$C_2+O_3<1/d$
, where
$d>0$
is sufficiently large and is only related to
$n,p$
and the growth of functions in the weighted Dirichlet spaces. Then all solutions of the (1.1) lie in
$\mathcal {D}^{p}_{\alpha }$
.
The second one is a variant of Theorem 1.2.
Corollary 3.3. Let
$0< p<\infty $
and
$\alpha>-1$
. Let n be a positive integer and
$A_i\in H(\mathbb {D})$
,
$i=0,1,\ldots ,n$
. Assume that the following statements hold:
$$ \begin{align*}K_1:=\int_{\mathbb{D}}|A_{n}(z)|^p(1-|z|^2)^{pn-p}dA_{\alpha}(z)<\infty,\end{align*} $$
$$ \begin{align*}Q_2:=\int_{\mathbb{D}}|A_{0}(z)|^p(1-|z|^2)^{pn-p-\alpha-2}dA_{\alpha}(z), \end{align*} $$
and
$$ \begin{align*}Q_3:=\sum_{i=1}^{n-1} \int_{\mathbb{D}}|A_i(z)|^p(1-|z|^2)^{p(n-i)-(2+\alpha)}dA_{\alpha}(z)\end{align*} $$
are two positive constants satisfying
$Q_2+Q_3<1/c$
, where
$c>0$
is sufficiently large and is only related to
$n,p$
. Then all solutions of the (1.1) lie in
$\mathcal {D}^{p}_{\alpha }$
.
Remark 3.4. Actually, in the proof of Theorem 1.2, by Lemma 2.6, we have
$$ \begin{align*} I_3\lesssim\|f_r\|^p_{\mathcal{D}^p_{\alpha}}\sum^{n-1}_{j=1}\int_{\mathbb{D}}\left|B_j(z)\right|^p(1-|z|^2)^{p(n-j)-(2+\alpha)}dA_{\alpha}(z)\leq Q_3\|f_r\|^p_{\mathcal{D}^p_{\alpha}}. \end{align*} $$
It is worth noting that the condition
$Q_3$
in the above corollary is stronger than the condition
$K_3$
in Theorem 1.2, which can be obtained by applying [Reference Zhu43, Proposition 4.13]
$$ \begin{align*}|f(z)|(1-|z|^2)^{p(n-i)}\lesssim\int_{\mathbb{D}}|f(w)|^p(1-|w|^2)^{p(n-j)-(2+\alpha)}dA_{\alpha}(w)\end{align*} $$
for any
$f\in H(\mathbb {D})$
.
Acknowledgements
The authors are grateful to the reviewer for his (or her) helpful comments.
