Hostname: page-component-6bf8c574d5-26wn4 Total loading time: 0 Render date: 2025-02-14T12:19:37.271Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex linear differential equations with solutions in weighted Dirichlet spaces and derivative Hardy spaces

Part of: Other generalizations Spaces and algebras of analytic functions Differential equations in the complex domain

Published online by Cambridge University Press:  06 January 2025

Qingze Lin Open the ORCID record for Qingze Lin [Opens in a new window]  and
Huayou Xie Open the ORCID record for Huayou Xie [Opens in a new window]
Qingze Lin
Affiliation:
Department of Mathematics, Shantou University, Shantou, 515063, China e-mail: gdlqz@e.gzhu.edu.cn
Huayou Xie*
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou, 510275, China
*
e-mail: xiehy33@mail2.sysu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, by the use of nth derivative characterization, we obtain several some sufficient conditions for all solutions of the complex linear differential equation

$$ \begin{align*}f^{(n)}+A_{n-1}(z)f^{(n-1)}+\ldots+A_1(z)f'+A_0(z)f=A_n(z) \end{align*} $$
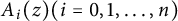to lie in weighted Dirichlet spaces and derivative Hardy spaces, respectively, where $A_i(z) (i=0,1,\ldots ,n)$ are analytic functions defined in the unit disc. This work continues the lines of the investigations by Heittokangas, et al. for growth estimates about the solutions of the above equation.

Keywords

Complex linear differential equationweighted Dirichlet spacesderivative Hardy spaces

MSC classification

Primary: 34M10: Oscillation, growth of solutions 30H05: Bounded analytic functions 31C25: Dirichlet spaces
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Q.L. is supported by STU Scientific Research Initiation Grant (No. NTF24015T)

References

Ahern, P. and Bruna, J., Maximal and area integral characterizations of Hardy-Sobolev spaces in the unit ball of ${C}^n$ . Rev. Mat. Iberoamericana 4(1988), no. 1, 123–153.Google Scholar
Allen, R. F., Heller, K. C., and Pons, M. A., Multiplication operators on ${S}^2(D)$ . Acta Sci. Math. (Szeged) 81(2015), no. 3–4, 575–587.Google Scholar
Arcozzi, N., Rochberg, R., and Sawyer, E., Carleson measures for analytic Besov spaces . Rev. Mat. Iberoamericana 18(2002), no. 2, 443–510.Google Scholar
Benbourenane, D. and Sons, L. R., On global solutions of complex differential equations in the unit disk . Complex Var. Theory Appl. 49(2004), no. 13, 913–925.Google Scholar
Chyzhykov, I., Gundersen, G., and Heittokangas, J., Linear differential equations and logarithmic derivative estimates . Proc. London Math. Soc. (3) 86(2003), no. 3, 735–754.Google Scholar
Contreras, M. D. and Hernández-Díaz, A. G., Weighted composition operators on spaces of functions with derivative in a Hardy space . J. Oper. Theory 52(2004), no. 1, 173–184.Google Scholar
Čučković, Ž. and Paudyal, B., Invariant subspaces of the shift plus complex Volterra operator . J. Math. Anal. Appl. 426(2015), no. 2, 1174–1181.Google Scholar
Čučković, Ž. and Paudyal, B., The lattices of invariant subspaces of a class of operators on the Hardy space . Arch. Math. (Basel) 110(2018), no. 5, 477–486.Google Scholar
Duren, P. L., Theory of ${H}^p$ spaces. Vol. 38, Pure and Applied Mathematics, Academic Press, New York, 1970.Google Scholar
Duren, P. L. and Schuster, A., Bergman spaces. Vol. 100, Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI, 2004.Google Scholar
Galanopoulos, P., Girela, D., and Peláez, J. Á., Multipliers and integration operators on Dirichlet spaces . Trans. Amer. Math. Soc. 363(2011), no. 4, 1855–1886.Google Scholar
Girela, D. and Peláez, J. Á., Carleson measures, multipliers and integration operators for spaces of Dirichlet type . J. Funct. Anal. 241(2006), no. 1, 334–358.Google Scholar
Girela, D. and Peláez, J. Á., Carleson measures for spaces of Dirichlet type . Integral Equ. Oper. Theory 55(2006), no. 3, 415–427.Google Scholar
Girela, D. and Peláez, J. Á., Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type . J. Aust. Math. Soc. 80(2006), no. 3, 397–418.Google Scholar
Gröhn, J., Huusko, J., and Rättyä, J., Linear differential equations with slowly growing solutions . Trans. Amer. Math. Soc. 370(2018), no. 10, 7201–7227.Google Scholar
Gu, C. and Luo, S., Composition and multiplication operators on the derivative Hardy space ${S}^2(D)$ . Complex Var. Elliptic Equ. 63(2018), no. 5, 599–624.Google Scholar
Gundersen, G. G., Steinbart, E. M., and Wang, S., The possible orders of solutions of linear differential equations with polynomial coefficients . Trans. Amer. Math. Soc. 350(1998), no. 3, 1225–1247.Google Scholar
Gupta, A. and Gupta, B., On $k$ -composition and $k$ -Hankel composition operators on the derivative Hardy space. Banach J. Math. Anal. 14(2020), no. 4, 1602–1629.Google Scholar
Heittokangas, J., On complex differential equations in the unit disc . In: Annales Academiae Scientiarum Fennicae Mathematica Dissertationes, 122, Ph.D. Dissertation, University of Joensuu, Joensuu, 2000, p. 54.Google Scholar
Heittokangas, J., Korhonen, R., and Rättyä, J., Growth estimates for solutions of linear complex differential equations . Ann. Acad. Sci. Fenn. Math. 29(2004), no. 1, 233–246.Google Scholar
Heittokangas, J., Korhonen, R., and Rättyä, J., Linear differential equations with coefficients in weighted Bergman and Hardy spaces . Trans. Amer. Math. Soc. 360(2008), no. 2, 1035–1055.Google Scholar
Heller, K., Composition operators on ${S}^2(D)$ . Ph.D. thesis, University of Virginia, 2010, p. 143.Google Scholar
Heller, K., Adjoints of linear fractional composition operators on ${S}^2(D)$ . J. Math. Anal. Appl. 394(2012), no. 2, 724–737.Google Scholar
Hu, G., Huusko, J., Long, J., and Sun, Y., Linear differential equations with solutions lying in weighted Fock spaces . Complex Var. Elliptic Equ. 66(2021), no. 2, 194–208.Google Scholar
Huusko, J., Korhonen, T., and Reijonen, A., Linear differential equations with solutions in the growth space ${H}_{\omega}^{\infty }$ . Ann. Acad. Sci. Fenn. Math. 41(2016), no. 1, 399–416.Google Scholar
Korhonen, R. and Rättyä, J., Linear differential equations in the unit disc with analytic solutions of finite order . Proc. Amer. Math. Soc. 135(2007), no. 5, 1355–1363.Google Scholar
Li, H. and Li, S., Nonlinear differential equation and analytic function spaces . Complex Var. Elliptic Equ. 63(2018), no. 1, 136–149.Google Scholar
Li, H. and Wulan, H., Linear differential equations with solutions in the ${Q}_K$ spaces. J. Math. Anal. Appl. 375(2011), no. 2, 478–489.Google Scholar
Lin, Q., The invariant subspaces of the shift plus integer multiple of the Volterra operator on Hardy spaces . Arch. Math. (Basel) 111(2018), no. 5, 513–522.Google Scholar
Lin, Q., Volterra type operators on weighted Dirichlet spaces . Chinese Ann. Math. Ser. B 42(2021), no. 4, 601–612.Google Scholar
Lin, Q., Order boundedness of weighted composition operators between two classes of function spaces (Chinese) . Acta Math. Sinica (Chinese Ser.) 65(2022), no. 2, 317–324.Google Scholar
Lin, Q., Liu, J., and Wu, Y., Volterra type operators on ${S}^p(D)$ spaces. J. Math. Anal. Appl. 461(2018), no. 2, 1100–1114.Google Scholar
Lin, Q., Liu, J., and Wu, Y., Order boundedness of weighted composition operators on weighted Dirichlet spaces and derivative Hardy spaces . Bull. Belg. Math. Soc. Simon Stevin 27(2020), no. 4, 627–637.Google Scholar
Luecking, D. H., Forward and reverse Carleson inequalities for functions in Bergman spaces and their derivatives . Amer. J. Math. 107(1985), no. 1, 85–111.Google Scholar
MacCluer, B. D., Composition operators on ${S}^p$ . Houston J. Math. 13(1987), no. 2, 245–254.Google Scholar
Novinger, W. P. and Oberlin, D. M., Linear isometries of some normed spaces of analytic functions . Canad. J. Math. 37(1985), no. 1, 62–74.Google Scholar
Pommerenke, Ch., On the mean growth of the solutions of complex linear differential equations in the disk . Complex Variables Theory Appl. 1(1982/83), no. 1, 23–38.Google Scholar
Roan, R. C., Composition operators on the space of functions with ${H}^p$ -derivative. Houston J. Math. 4(1978), no. 3, 423–438.Google Scholar
Sun, Y., Liu, J., and Hu, G., Complex linear differential equations with solutions in the ${H}_K^2$ spaces. Complex Var. Elliptic Equ. 67(2022), no. 11, 2577–2588.Google Scholar
Sun, Y., Liu, B., and Liu, J. L., Complex linear differential equations with solutions in Dirichlet-Morrey spaces . Anal. Math. 49(2023), no. 1, 295–306.Google Scholar
Wu, Z., Carleson measures and multipliers for Dirichlet spaces . J. Funct. Anal. 169(1999), no. 1, 148–163.Google Scholar
Xiao, L., Differential equations with solutions lying in the $F(p,q,s)$ space. Complex Var. Elliptic Equ. 63(2018), no. 1, 116–135.Google Scholar
Zhu, K., Operator theory in function spaces. 2nd ed., Mathematical Surveys and Monographs, 138, American Mathematical Society, Providence, RI, 2007.Google Scholar