In this paper, we study existence of rotating periodic solutions for p-Laplacian differential systems. We first build a new continuation theorem by topological degree, and then obtain the existence of rotating periodic solutions for two kinds of p-Laplacian differential systems via this continuation theorem, extend some existing relevant results.

This paper aims to investigate the existence of periodic solutions for $p$-Laplacian differential equations with jumping nonlinearity under the frame of half-eigenvalue. Based on the continuity theorem, some new results are obtained, which enrich and generalize the previous results.

In this paper we study two weak notions of Jacobian determinant for Sobolev maps, namely the distributional Jacobian and the relaxed total variation, which in general could be different. We show some cases of equality and use them to give an explicit expression for the relaxation of some polyconvex functionals.

We establish the existence of positive solutions of the Sturm–Liouville problem

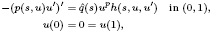
where

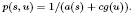
We assume g and 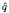to be non-negative, continuous functions, a(s) is a positive continuous function, c≥0, p>1, and the function h is sub-quadratic with respect to u′. We combine a priori estimates with a fixed-point result of Krasnosel'skii to obtain the existence of a positive solution.

We study a class of second-order nonlinear differential equations on a finite interval with periodic boundary conditions. The nonlinearity in the equations can take negative values and may be unbounded from below. Criteria are established for the existence of non-trivial solutions, positive solutions and negative solutions of the problems under consideration. Applications of our results to related eigenvalue problems are also discussed. Examples are included to illustrate some of the results. Our analysis relies mainly on topological degree theory.

The paper is devoted to analysis of an elliptic-algebraic system ofequations describing heat explosion in a two phase medium filling a star-shaped domain. Three typesof solutions are found: classical, critical andmultivalued. Regularity of solutions is studied as well as theirbehavior depending on the size of the domain and on the coefficient ofheat exchange between the two phases. Critical conditions of existence of solutions are found for arbitrary positive source function.