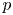1. Introduction
In this paper, we consider the existence of periodic solutions of $p$![]() -Laplacian differential equations with jumping nonlinearity of variable coefficients as follows.
-Laplacian differential equations with jumping nonlinearity of variable coefficients as follows.
where $W_{0}(t,u)=g_{0}(u)+g_{1}(t,u)$![]() , $W_{1}(t,u,u')=\overline {g}_{0}(u)+\overline {g}_{1}(t,u')$
, $W_{1}(t,u,u')=\overline {g}_{0}(u)+\overline {g}_{1}(t,u')$![]() ; $g_{0},\overline {g}_{0}\in C(\mathbb {R},\mathbb {R})$
; $g_{0},\overline {g}_{0}\in C(\mathbb {R},\mathbb {R})$![]() ; $g_{1},\overline {g}_{1}\in C([0,T]\times \mathbb {R},\mathbb {R})$
; $g_{1},\overline {g}_{1}\in C([0,T]\times \mathbb {R},\mathbb {R})$![]() and are $T$
and are $T$![]() -periodic in $t$
-periodic in $t$![]() ; $a_{\pm }\in C([0,T],(0,\infty ))$
; $a_{\pm }\in C([0,T],(0,\infty ))$![]() and are $T$
and are $T$![]() -periodic in $t$
-periodic in $t$![]() ; $e\in C([0,T],\mathbb {R})$
; $e\in C([0,T],\mathbb {R})$![]() and is $T$
and is $T$![]() -periodic in $t$
-periodic in $t$![]() ; $\phi _{p}(s)=|s|^{p-2}s \ (s\neq 0)$
; $\phi _{p}(s)=|s|^{p-2}s \ (s\neq 0)$![]() , $\phi _{p}(0)=0$
, $\phi _{p}(0)=0$![]() , $1< p<\infty$
, $1< p<\infty$![]() , $1/p+1/q=1;$
, $1/p+1/q=1;$![]() $u^{+}(t) = \max \{ u(t),0\}$
$u^{+}(t) = \max \{ u(t),0\}$![]() , $u^{-}(t) = \max \{- u(t),0\}.$
, $u^{-}(t) = \max \{- u(t),0\}.$![]()
In several decades ago, Dancer [Reference Dancer6] and Fučik [Reference Fučik11] presented the definition of the Dancer–Fučik spectrum for second-order linear differential equation with periodic boundary condition, which is a generalization of the common spectrum. Since then, many scholars devoted to investigating the existence of periodic solutions for second-order non-dissipative differential equation under the frame of Dancer–Fučik spectrum when asymptotic behaviours of potential function are given (see [Reference Ding and Zanolin8–Reference Fabry10, Reference Gossez and Omari13, Reference Liu and Li16, Reference Morris and Robinson20, Reference Nkashama and Robinson21, Reference Zhang27] and references therein). After that, Del Pino, Manásevich, Murúa [Reference Del Pino, Manásevich and Murúa7] gave the concept of Dancer–Fučik spectrum for second-order $p$![]() -Laplacian differential equation with periodic boundary condition, i.e., if there exists a pair of positive constants $(\alpha,\beta )$
-Laplacian differential equation with periodic boundary condition, i.e., if there exists a pair of positive constants $(\alpha,\beta )$![]() such that
such that
has a nontrivial solutions, then we say that $(\alpha,\beta )$![]() lies in the Dancer–Fučik spectrum $S_{p}$
lies in the Dancer–Fučik spectrum $S_{p}$![]() of the problem (). In the case $p=2$
of the problem (). In the case $p=2$![]() , the set $S_{2}$
, the set $S_{2}$![]() is the classical Dancer–Fučik spectrum. It is known that the set $S_{p}$
is the classical Dancer–Fučik spectrum. It is known that the set $S_{p}$![]() has the structure (see [Reference Del Pino, Manásevich and Murúa7]) $S_{p}=\bigcup _{k=0}^{+\infty }C_{k}$
has the structure (see [Reference Del Pino, Manásevich and Murúa7]) $S_{p}=\bigcup _{k=0}^{+\infty }C_{k}$![]() , where
, where

in which $n\geq 1$![]() and $\pi _p$
and $\pi _p$![]() is given by
is given by

The problem (1.3) is non-resonant if and only if $(\alpha,\beta )\notin S_{p}$![]() , otherwise it is resonant. The Dancer–Fučik spectrum $S_{p}$
, otherwise it is resonant. The Dancer–Fučik spectrum $S_{p}$![]() has been used to investigate the existence of solutions of the following $p$
has been used to investigate the existence of solutions of the following $p$![]() -Laplacian problem.
-Laplacian problem.
where $g(t,u)\in C([0,T]\times \mathbb {R},\mathbb {R})$![]() . Assuming that the potential function $g$
. Assuming that the potential function $g$![]() satisfies the following asymptotic estimates.
satisfies the following asymptotic estimates.
where $p_i,q_i, i=1.2$![]() are positive constant satisfying
are positive constant satisfying
then existence results for periodic solutions have been obtained using Leray–Schauder degree theory and the comparison argument, see [Reference Del Pino, Manásevich and Murúa7]. The condition (1.7) extends the preceding idea of non-resonance ($(\alpha,\beta )\notin S_{p}$![]() ), in the sense that the asymptotes of the ratio $\frac {g(u)}{|u|^{p-2}u}$
), in the sense that the asymptotes of the ratio $\frac {g(u)}{|u|^{p-2}u}$![]() are now forced to lie in the rectangle $[p_1,p_2]\times [q_1,q_2]\subset \mathbb {R}^{2}$
are now forced to lie in the rectangle $[p_1,p_2]\times [q_1,q_2]\subset \mathbb {R}^{2}$![]() , and this rectangle lies between two consecutive curves of the spectrum $S_{p}$
, and this rectangle lies between two consecutive curves of the spectrum $S_{p}$![]() , so does not intersect $S_{p}$
, so does not intersect $S_{p}$![]() .
.
A further extension was introduced by Nkashama and Robinson [Reference Nkashama and Robinson21] in the case $p = 2$![]() . This extension uses an averaging method to allow the asymptotes of the above ratio to cross the spectrum $S_{p}$
. This extension uses an averaging method to allow the asymptotes of the above ratio to cross the spectrum $S_{p}$![]() , so long as suitable averages of this ratio do not. This averaging method was extended to more general $p$
, so long as suitable averages of this ratio do not. This averaging method was extended to more general $p$![]() by Chang and Qiao in [Reference Chang and Qiao5]. The non-resonance condition in [Reference Chang and Qiao5] assumes that $g$
by Chang and Qiao in [Reference Chang and Qiao5]. The non-resonance condition in [Reference Chang and Qiao5] assumes that $g$![]() satisfies
satisfies
with $([p_1,p_2]\times [q_1,q_2])\cap S_{p}=\emptyset,$![]() where $G(t,u)=\int _{0}^{u}g(t,s)\,{\rm d}s.$
where $G(t,u)=\int _{0}^{u}g(t,s)\,{\rm d}s.$![]() Since
Since
we see that the former non-resonance condition (1.7), in terms of $\frac {{g(t,u)}}{{|u|^{p - 2} u}}$![]() , implies the latter condition (1.8) and (1.9), that is, the latter condition is more general. In [Reference Liu and Li17], Liu and Li considered the classical oscillation equation with $p$
, implies the latter condition (1.8) and (1.9), that is, the latter condition is more general. In [Reference Liu and Li17], Liu and Li considered the classical oscillation equation with $p$![]() -Laplacian operator as follows.
-Laplacian operator as follows.
where $g$![]() satisfies
satisfies
and $(\omega,\nu )\notin S_{p}.$![]() Clearly, the (1.10) implies the (1.8) and (1.9) when $g$
Clearly, the (1.10) implies the (1.8) and (1.9) when $g$![]() is autonomous. Under the condition that there exist positive constants $\ b, \ d_{1}, \ d_{2}$
is autonomous. Under the condition that there exist positive constants $\ b, \ d_{1}, \ d_{2}$![]() such that $\ d_{1}\leq \frac {{g(u)}}{{|u|^{p - 2} u}}\leq d_{2} \ \mbox {for all} \ |u|\geq b$
such that $\ d_{1}\leq \frac {{g(u)}}{{|u|^{p - 2} u}}\leq d_{2} \ \mbox {for all} \ |u|\geq b$![]() , which is different from the assumptions given in [Reference Chang and Qiao5], the existence of periodic solutions was obtained. For more articles concerning this topic, the readers can refer to [Reference Anane and Dakkak1, Reference Jiang14, Reference Liu15, Reference Yang26] and its references.
, which is different from the assumptions given in [Reference Chang and Qiao5], the existence of periodic solutions was obtained. For more articles concerning this topic, the readers can refer to [Reference Anane and Dakkak1, Reference Jiang14, Reference Liu15, Reference Yang26] and its references.
Recently, Binding and Rynne [Reference Binding and Rynne3] presented the concept of half-eigenvalue for the following $p$![]() -Laplacian differential equations with periodic boundary condition, i.e., if $\lambda$
-Laplacian differential equations with periodic boundary condition, i.e., if $\lambda$![]() is constant such that the following problem
is constant such that the following problem

possesses a nontrivial solution, then $\lambda$![]() is termed half-eigenvalue. Let $\sigma =\bigcup _{m=0}^{+\infty }\sigma _{m}$
is termed half-eigenvalue. Let $\sigma =\bigcup _{m=0}^{+\infty }\sigma _{m}$![]() , where
, where
By Prüfer approach, the characteristics of the set $\sigma$![]() were also given (see [18, theorem 3.1]). It contains two sequences of half-eigenvalues $\{\lambda _{2m}^{min}\}_{m\in \mathbb {Z}^{+}}$
were also given (see [18, theorem 3.1]). It contains two sequences of half-eigenvalues $\{\lambda _{2m}^{min}\}_{m\in \mathbb {Z}^{+}}$![]() and $\{\lambda _{2m}^{max}\}_{m\in \mathbb {Z}^{+}}$
and $\{\lambda _{2m}^{max}\}_{m\in \mathbb {Z}^{+}}$![]() that satisfy
that satisfy
$\sigma _{0}=\{\lambda _{0}^{min},\lambda _{0}^{max}\}$![]() . Moreover, if we regard the half eigenvalues $\lambda _{n}^{{\rm max,min}}$
. Moreover, if we regard the half eigenvalues $\lambda _{n}^{{\rm max,min}}$![]() as functions of the coefficient pairs $(a^{+}, a^{-})$
as functions of the coefficient pairs $(a^{+}, a^{-})$![]() , i.e., $\lambda _{n}^{{\rm max,min}}(a^{+}, a^{-})$
, i.e., $\lambda _{n}^{{\rm max,min}}(a^{+}, a^{-})$![]() , and we suppose that ${a_{\pm }\in L^{\gamma }}$
, and we suppose that ${a_{\pm }\in L^{\gamma }}$![]() , it was shown in Li and Yan [Reference Li and Yan18] that $\lambda _{n}^{{\rm max,min}}(a^{+}, a^{-})$
, it was shown in Li and Yan [Reference Li and Yan18] that $\lambda _{n}^{{\rm max,min}}(a^{+}, a^{-})$![]() depends continuously on $(a^{+}, a^{-})$
depends continuously on $(a^{+}, a^{-})$![]() , with respect to the weak topology on $(L^{\gamma })^{2}$
, with respect to the weak topology on $(L^{\gamma })^{2}$![]() . Furthermore, it should be mentioned that if $a_{\pm }$
. Furthermore, it should be mentioned that if $a_{\pm }$![]() are constants, (1.11) becomes
are constants, (1.11) becomes
where $\widetilde {a}_{\pm }=a_{\pm }+\lambda$![]() . Clearly, it reduces to the problem of Dancer–Fučik spectrum.
. Clearly, it reduces to the problem of Dancer–Fučik spectrum.
For the problems of half-eigenvalues with variable coefficients, it can be traced back to [Reference Berestycki2, Reference Browne4]. After that, more and more scholars devoted to investigating half-eigenvalues with different boundary value problems. For the aspects of existence of solutions, recently, based on the Landesman–Lazer conditions, Genoud and Rynne [Reference Genoud and Rynne12] made use of the shooting method to investigate the existence of solutions for $p$![]() -Laplacian differential equations with Dirichlet boundary condition under the frame of half-eigenvalue as follows.
-Laplacian differential equations with Dirichlet boundary condition under the frame of half-eigenvalue as follows.
Rynne [Reference Rynne22] made a further study on this type of problem with the dissipation term. For more papers concerning this topic, we refer to Rynne [Reference Rynne23–Reference Rynne25] and references therein. However, it should be pointed out that there are few works on discussing the existence of periodic solutions for $p$![]() -Laplacian problems with jumping nonlinearities under the frame of half-eigenvalue.
-Laplacian problems with jumping nonlinearities under the frame of half-eigenvalue.
Motivated by the works mentioned above, our paper aims to investigate the existence of periodic solutions of $p$![]() -Laplacian differential equations with jump nonlinearity of variable coefficients under the frame of half-eigenvalue. The variable coefficients and $p$
-Laplacian differential equations with jump nonlinearity of variable coefficients under the frame of half-eigenvalue. The variable coefficients and $p$![]() -Laplacian operator bring many difficulties such as the prior estimation and convergence analysis. We make use of some analytical skills and the continuity theorem to overcome these difficulties and obtain some new results, which generalize the existence of periodic solutions under the framework of Dancer–Fučik spectral with constant coefficients to the case of half-eigenvalues with variable coefficients. Moreover, the model is more general and complex.
-Laplacian operator bring many difficulties such as the prior estimation and convergence analysis. We make use of some analytical skills and the continuity theorem to overcome these difficulties and obtain some new results, which generalize the existence of periodic solutions under the framework of Dancer–Fučik spectral with constant coefficients to the case of half-eigenvalues with variable coefficients. Moreover, the model is more general and complex.
2. Main results
To begin with, we show some necessary basic knowledge and signs. Let $C([0,T],\mathbb {R})$![]() with norm $\| u \|_{\infty }={\max }_{t\in [0,T]}|u(t)|$
with norm $\| u \|_{\infty }={\max }_{t\in [0,T]}|u(t)|$![]() and $L^{p}([0,T],\mathbb {R})$
and $L^{p}([0,T],\mathbb {R})$![]() with norm $\| u \|_{p}=\left (\int _{0}^{T}|u(t)|^{p} {\rm d}t\right )^{\frac {1}{p}}.$
with norm $\| u \|_{p}=\left (\int _{0}^{T}|u(t)|^{p} {\rm d}t\right )^{\frac {1}{p}}.$![]() Set $a_{\pm,M}={\max }_{t\in [0,T]}a_{\pm }(t)$
Set $a_{\pm,M}={\max }_{t\in [0,T]}a_{\pm }(t)$![]() , $a_{\pm,L}={\min }_{t\in [0,T]}a_{\pm }(t)$
, $a_{\pm,L}={\min }_{t\in [0,T]}a_{\pm }(t)$![]() . And define the following Banach space
. And define the following Banach space
endowed the norm $\|u\|=\max \{\| u \|_{\infty },\| u' \|_{\infty }\}.$![]()
Next, let us introduce the famous continuity theorem for $p$![]() -Laplacian equation.
-Laplacian equation.
Lemma 2.1 [Reference Manásevich and Mawhin19]
Assume that $\Omega$![]() is an open bounded set in $C_{T}^{1}$
is an open bounded set in $C_{T}^{1}$![]() such that the following conditions hold:
such that the following conditions hold:
${ (i)}$![]() For each $\lambda \in (0,1)$
For each $\lambda \in (0,1)$![]() , the problem
, the problem
has no solution on $\partial \Omega$![]() .
.
${(ii)}$![]() The equation
The equation
has no solution on $\partial \Omega \cap \mathbb {R}$![]() .
.
${(iii)}$![]() The Brouwer degree
The Brouwer degree
Then, when $\lambda =1$![]() , the problem (2.1) has a solution in $\overline {\Omega }$
, the problem (2.1) has a solution in $\overline {\Omega }$![]() .
.
Remark 2.2 In lemma 2.1, it should be mentioned that for given $f$![]() , a is being regarded as a constant function for $\partial \Omega \cap \mathbb {R}$
, a is being regarded as a constant function for $\partial \Omega \cap \mathbb {R}$![]() to make sense.
to make sense.
In order to get our main results of problems (1.1) and (1.2), we first consider the existence of periodic solutions for the following auxiliary dissipative problems.
and

where $\varepsilon >0$![]() is a constant and $\hbar$
is a constant and $\hbar$![]() represents a symbol defined by
represents a symbol defined by

Now, we introduce some auxiliary lemmas.
Lemma 2.3 For $2\leq p<\infty$![]() , assume that the following conditions hold.
, assume that the following conditions hold.
$(H1)$![]() There exist nonnegative functions $a_{i}>0,i=1.2,$
There exist nonnegative functions $a_{i}>0,i=1.2,$![]() and constant $\theta \in [0,p-1)$
and constant $\theta \in [0,p-1)$![]() such that for $(t,u)\in [0,T]\times \mathbb {R}$
such that for $(t,u)\in [0,T]\times \mathbb {R}$![]() ,
,
$(H2)$![]() There exists constant $a_{3}>0$
There exists constant $a_{3}>0$![]() such that if $|u|>a_{3}$
such that if $|u|>a_{3}$![]() , for $t\in [0,T],u\in \mathbb {R}$
, for $t\in [0,T],u\in \mathbb {R}$![]() ,
,
or
Then the problem (2.4) has at least one solution.
Proof. Consider the following homotopy equation with periodic boundary condition
where $\lambda \in (0,1)$![]() .
.
First, if $u\in C_{T}^{1}$![]() is a solution of (2.6), we claim that there exist positive constants $b_{i},i=1,2$
is a solution of (2.6), we claim that there exist positive constants $b_{i},i=1,2$![]() such that $\|u\|_{\infty }\leq b_{1}+b_{2}\|u'\|_{{1}}$
such that $\|u\|_{\infty }\leq b_{1}+b_{2}\|u'\|_{{1}}$![]() . Let $t_{1}$
. Let $t_{1}$![]() and $t_{2}$
and $t_{2}$![]() represent minimum and maximum points respectively. Thus, we know that
represent minimum and maximum points respectively. Thus, we know that
Thus, we need to consider the following three cases.

For the case (A1), it is clear that $\|u\|_{\infty }\leq \|u'\|_{{1}}$![]() . For the case (A2), from (2.6), we have
. For the case (A2), from (2.6), we have
and
Thus, we know that
i.e., there exists $t_{3}\in [0,T]$![]() such that
such that
From $(H2)$![]() , we can obtain that $|u(t_{3})|\leq a_{3}.$
, we can obtain that $|u(t_{3})|\leq a_{3}.$![]() Thus, the claim is proved. By the similar way to the case $(A2)$
Thus, the claim is proved. By the similar way to the case $(A2)$![]() , the case $(A3)$
, the case $(A3)$![]() is also true. Here, we omit the detail.
is also true. Here, we omit the detail.
Multiplying the both sides of (2.6) by $u'$![]() and integrating from $0$
and integrating from $0$![]() to $T$
to $T$![]() , we have
, we have

By the definition of $\hbar$![]() , we get two cases as follows.
, we get two cases as follows.

Moreover, by $(H1)$![]() and the basic inequality $(x+y)^{r}\leq 2^{r}(x^{r}+y^{r}), x,y,r>0$
and the basic inequality $(x+y)^{r}\leq 2^{r}(x^{r}+y^{r}), x,y,r>0$![]() , we have
, we have

Thus, from (i) or (ii), we have

So, we can get

Noting that $\theta \in [0,p-1)$![]() , we claim that $\|u'\|_{{p}}$
, we claim that $\|u'\|_{{p}}$![]() is bounded, i.e, there exists a positive constant $D$
is bounded, i.e, there exists a positive constant $D$![]() such that $\|u'\|_{{p}}\leq D$
such that $\|u'\|_{{p}}\leq D$![]() . Otherwise, we can find the sequence $\{u'_{n}(t)\}_{n\in \mathbb {Z^{+}}}$
. Otherwise, we can find the sequence $\{u'_{n}(t)\}_{n\in \mathbb {Z^{+}}}$![]() which satisfies (2.8) such that
which satisfies (2.8) such that
Moreover, multiplying (2.8) by $\frac {1}{\|u'_{n}\|_{{p}}^{\theta }}$![]() , since $\theta \in [0,p-1)$
, since $\theta \in [0,p-1)$![]() , we have
, we have

which implies a contradiction as $n\to \infty$![]() . Thus, the claim is true. Therefore, we have
. Thus, the claim is true. Therefore, we have
On the other hand, (2.6) is equivalent to
Since $u(0)=u(T)$![]() , there exists $t^{*}\in (0,T)$
, there exists $t^{*}\in (0,T)$![]() such that $u'(t^{*})=0$
such that $u'(t^{*})=0$![]() . Integrating from $t^{*}$
. Integrating from $t^{*}$![]() to $t$
to $t$![]() on (2.9), we have
on (2.9), we have

Thus, we can obtain
where $l={\max }_{|u|\leq \overline {D},0\leq t\leq T}|W_{0}(t,u(t))|$![]() . It implies that $\|u'\|_{\infty }\leq K.$
. It implies that $\|u'\|_{\infty }\leq K.$![]()
Let
where $M>K+\overline {D}$![]() such that $a_{+}(t)\phi _{p}(M+1)+W_{0}(t,M+1)-e(t)>0$
such that $a_{+}(t)\phi _{p}(M+1)+W_{0}(t,M+1)-e(t)>0$![]() and $a_{-}(t)\phi _{p}(-M-1)+W_{0}(t,-M-1)-e(t)<0$
and $a_{-}(t)\phi _{p}(-M-1)+W_{0}(t,-M-1)-e(t)<0$![]() . Clearly, the problem (2.4) has no solution on $\mathbb {R}\cap \partial \Omega$
. Clearly, the problem (2.4) has no solution on $\mathbb {R}\cap \partial \Omega$![]() . Moreover, we can get
. Moreover, we can get

Thus, $F(a)$![]() has no solution on $\mathbb {R}\cap \partial \Omega$
has no solution on $\mathbb {R}\cap \partial \Omega$![]() . Making a homotopy
. Making a homotopy

where $u\in \mathbb {R}\cap \partial \Omega$![]() , we have
, we have

Based on the homotopic transformation, we have
Thus, the problem (2.4) has at least one solution.
Lemma 2.4 For $1< p<\infty,$![]() assume that the following conditions hold.
assume that the following conditions hold.
$(H3)$![]() There exist functions $a_{i}>0,i=1.2,$
There exist functions $a_{i}>0,i=1.2,$![]() and constant $\theta \in [0,p-1)$
and constant $\theta \in [0,p-1)$![]() such that for $(t,v)\in [0,T]\times \mathbb {R},$
such that for $(t,v)\in [0,T]\times \mathbb {R},$![]()
$(H4)$![]() There exist positive constants $\varrho,$
There exist positive constants $\varrho,$![]() $d$
$d$![]() and $\gamma \in (0,p-1]$
and $\gamma \in (0,p-1]$![]() such that for $t\in [0,T]$
such that for $t\in [0,T]$![]() ,
,
Then the problem (2.5) has at least one solution.
Proof. First, we can obtain the priori estimate that if $u\in C_{T}^{1}$![]() is a solution of the problem (2.5), then we have $|u(t)|\leq L,$
is a solution of the problem (2.5), then we have $|u(t)|\leq L,$![]() where $L$
where $L$![]() is a positive constant and independent of $\lambda$
is a positive constant and independent of $\lambda$![]() . Otherwise, we can find solutions $\{u_{n}(t)\}$
. Otherwise, we can find solutions $\{u_{n}(t)\}$![]() of the problem (2.5) corresponding with $\lambda =\lambda _{n}$
of the problem (2.5) corresponding with $\lambda =\lambda _{n}$![]() , namely, $u_{n}(t)$
, namely, $u_{n}(t)$![]() satisfies the following equation
satisfies the following equation

and periodic boundary condition such that
For any $u \in C_{T}^{1}\setminus \{0\}$![]() , let $z_{n}(t)=\frac {u_{n}(t)}{\left \| u_{n} \right \|_{\infty }}$
, let $z_{n}(t)=\frac {u_{n}(t)}{\left \| u_{n} \right \|_{\infty }}$![]() , so $\|z_{n}\|_{\infty }=1$
, so $\|z_{n}\|_{\infty }=1$![]() . Moreover, multiplying (2.11) by $\frac {u_{n}'}{\left \| u_{n} \right \|^{p}_{\infty }}$
. Moreover, multiplying (2.11) by $\frac {u_{n}'}{\left \| u_{n} \right \|^{p}_{\infty }}$![]() and integrating from 0 to $T$
and integrating from 0 to $T$![]() , we have
, we have

By definition of $\hbar$![]() , we get two cases as follows.
, we get two cases as follows.

By $(H3)$![]() , we can get
, we can get

Thus, from (i) or (ii), one has

which yields that

We claim that $\|z_{n}'\|_{{p}}\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . If not, we have the following two cases.
. If not, we have the following two cases.
For the case $(B1)$![]() , from (2.13), we have
, from (2.13), we have

which implies that $\varepsilon c^{p-1}\leq 0$![]() as $n\to \infty$
as $n\to \infty$![]() . This is impossible. Clearly, for the case $(B2)$
. This is impossible. Clearly, for the case $(B2)$![]() , we can also get a contradiction. Thus, $\|z_{n}'\|_{{p}}\to 0$
, we can also get a contradiction. Thus, $\|z_{n}'\|_{{p}}\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . Moreover, for any $t\in [0,T]$
. Moreover, for any $t\in [0,T]$![]() , by Hölder inequality, we have
, by Hölder inequality, we have

Since $\|z_{n}\|=1$![]() , we can obtain
, we can obtain
Thus, we have
Similarly, we have

Clearly, $\|u'_{n}\|_{{p}}$![]() is bounded, i.e, there exists a positive constant $\overline {L}$
is bounded, i.e, there exists a positive constant $\overline {L}$![]() such that ${\|u'_{n}\|_{{p}}\leq \overline {L}}$
such that ${\|u'_{n}\|_{{p}}\leq \overline {L}}$![]() . Otherwise,
. Otherwise,
From (2.15), we have

which implies a contradiction. Thus, $\|u'_{n}\|_{{p}}$![]() is bounded. Moreover, we can also get
is bounded. Moreover, we can also get

and

By $(H4)$![]() , we have
, we have

which implies that

However, integrating from 0 to $T$![]() on (2.11), we have
on (2.11), we have

This implies a contradiction for $n$![]() large enough. Therefore, $|u(t)|\leq L$
large enough. Therefore, $|u(t)|\leq L$![]() . By the similar way to lemma 2.2, we can obtain that there exists a positive constant $\Theta$
. By the similar way to lemma 2.2, we can obtain that there exists a positive constant $\Theta$![]() such that $|u'(t)|\leq \Theta$
such that $|u'(t)|\leq \Theta$![]() . Moreover, $\mbox {deg}_{B}(F,\mathbb {R}\cap \partial \Omega,0)\neq 0$
. Moreover, $\mbox {deg}_{B}(F,\mathbb {R}\cap \partial \Omega,0)\neq 0$![]() . Thus, the problem (2.5) has at least one solution.
. Thus, the problem (2.5) has at least one solution.
Remark 2.5 In view of the continuity theorem, the key step is to obtain a priori bound estimation of solutions. In fact, if $W_{1}(t,u,u')$![]() is written as $\overline {g}_{0}(u)+\overline {g}_{1}(t,u,u')$
is written as $\overline {g}_{0}(u)+\overline {g}_{1}(t,u,u')$![]() , by the method used in lemma 2.3, we can not get (2.13) that make us fail to obtain the prior estimation when $1< p<\infty$
, by the method used in lemma 2.3, we can not get (2.13) that make us fail to obtain the prior estimation when $1< p<\infty$![]() .
.
Now, we state and prove our main results for problems (1.1) and (1.2).
Theorem 2.6 For $2\leq p<\infty$![]() , assume that $(H1)$
, assume that $(H1)$![]() and the following conditions hold.
and the following conditions hold.
$(H5)$![]() There exist positive constants $\delta,\ \zeta,\ d$
There exist positive constants $\delta,\ \zeta,\ d$![]() such that for $t\in [0,T],$
such that for $t\in [0,T],$![]()
$(H6)$![]() $\mathop {\lim }\limits _{|u| \to \infty } \frac {{pG_{0}(u)}}{{|u|^{p} }} = \eta,$
$\mathop {\lim }\limits _{|u| \to \infty } \frac {{pG_{0}(u)}}{{|u|^{p} }} = \eta,$![]() where $\eta \in (0,\infty )\setminus \bigcup _{k=0}^{\infty }[\lambda _{2k}^{min},\lambda _{2k}^{max}]$
where $\eta \in (0,\infty )\setminus \bigcup _{k=0}^{\infty }[\lambda _{2k}^{min},\lambda _{2k}^{max}]$![]() .
.
Then the problem (1.1) has at least one solution.
Proof. In view of lemma 2.3, we claim that if $\{u_n(t)\}$![]() are solutions of the problem (2.4) corresponding to $\varepsilon = \{\varepsilon _n\}$
are solutions of the problem (2.4) corresponding to $\varepsilon = \{\varepsilon _n\}$![]() , where $\varepsilon _n\to 0$
, where $\varepsilon _n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , then there exist constants $\widetilde {D},\ \widetilde {K}>0$
, then there exist constants $\widetilde {D},\ \widetilde {K}>0$![]() , independent of $\varepsilon _n$
, independent of $\varepsilon _n$![]() , such that for $t\in [0,T]$
, such that for $t\in [0,T]$![]() ,
,
Otherwise,
For any $u \in C_{T}^{1}\setminus \{0\}$![]() , let $z_{n}(t)=\frac {u_{n}(t)}{\left \| u_{n} \right \|_{\infty }}$
, let $z_{n}(t)=\frac {u_{n}(t)}{\left \| u_{n} \right \|_{\infty }}$![]() , so $\|z_{n}\|_{\infty }=1$
, so $\|z_{n}\|_{\infty }=1$![]() . Moreover, dividing the problem (2.4) by $\left \| u_{n} \right \|_{\infty }^{p-1}$
. Moreover, dividing the problem (2.4) by $\left \| u_{n} \right \|_{\infty }^{p-1}$![]() , we have
, we have

which is equivalent to

Since $z_{n}(0)=z_{n}(T)$![]() , there exists $t_{*}\in (0,T)$
, there exists $t_{*}\in (0,T)$![]() such that $z_{n}'(t_{*})=0$
such that $z_{n}'(t_{*})=0$![]() . Thus, we have
. Thus, we have

From $\varepsilon _{n} \to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , there exists a positive constant $d_{1}$
, there exists a positive constant $d_{1}$![]() such that $e^{\varepsilon _{n}\hbar t}\leq d_{1}$
such that $e^{\varepsilon _{n}\hbar t}\leq d_{1}$![]() . Moreover, we have
. Moreover, we have

which implies that there exists a constant $M_{1}>0$![]() which is independent of $n$
which is independent of $n$![]() such that
such that

Based on $\|z_{n}\|=1$![]() and $(H5)$
and $(H5)$![]() , for any $t \in [0,T]$
, for any $t \in [0,T]$![]() , there exists a constant $M_{2}>0$
, there exists a constant $M_{2}>0$![]() which is independent of $n$
which is independent of $n$![]() such that
such that

which together with $e\in C([0,T])$![]() and the monotonicity of $\phi _{p}(\cdot )$
and the monotonicity of $\phi _{p}(\cdot )$![]() yield that
yield that
where $M_{3}>0$![]() is a constant and independent of $n$
is a constant and independent of $n$![]() . Thus, from the definition of $z_{n}(t)$
. Thus, from the definition of $z_{n}(t)$![]() , it follows that $z_{n}(t)$
, it follows that $z_{n}(t)$![]() is uniformly bounded. By the standard argument, we can get that $z_{n}(t)$
is uniformly bounded. By the standard argument, we can get that $z_{n}(t)$![]() is also equicontinuous. Moreover, from (2.22), we can also find a constant $M_{4}>0$
is also equicontinuous. Moreover, from (2.22), we can also find a constant $M_{4}>0$![]() which is independent of $n$
which is independent of $n$![]() such that
such that
Furthermore, $\forall t_{1},\ t_{2}\in [0,1]$![]() , assuming that $t_{1}\leq t_{2},$
, assuming that $t_{1}\leq t_{2},$![]() for any $n\in \mathbb {N}$
for any $n\in \mathbb {N}$![]() , we have
, we have

which together with the monotonicity and uniformly continuity of $\phi _{p}(\cdot )$![]() on $[-M_{3}^{q-1},M_{3}^{q-1}]$
on $[-M_{3}^{q-1},M_{3}^{q-1}]$![]() yield that $z_{n}'(t)$
yield that $z_{n}'(t)$![]() is also uniformly bounded and equicontinuous. By Arzelá–Ascoli theorem, there exists a subsequence of $\{z_{n}\}$
is also uniformly bounded and equicontinuous. By Arzelá–Ascoli theorem, there exists a subsequence of $\{z_{n}\}$![]() (without loss of generality, take its subsequence) and $z(t)\in C_{T}^{1}$
(without loss of generality, take its subsequence) and $z(t)\in C_{T}^{1}$![]() such that for any $t\in [0,T]$
such that for any $t\in [0,T]$![]() ,
,
Thus, there exists a $\widetilde {t}\in [0,T]$![]() such that $z(\widetilde {t})\neq 0.$
such that $z(\widetilde {t})\neq 0.$![]() Multiplying both sides of (2.4) by $\frac {u_{n}'(t)}{\|u_{n}\|^{p}}$
Multiplying both sides of (2.4) by $\frac {u_{n}'(t)}{\|u_{n}\|^{p}}$![]() and integrating from $\widetilde {t}$
and integrating from $\widetilde {t}$![]() to $t$
to $t$![]() , one has
, one has

Following $(H4)$![]() , we know that
, we know that
For any $\epsilon >0$![]() , there exists a constant $l_{1}>0$
, there exists a constant $l_{1}>0$![]() such that
such that
By the continuity of $G_{0}$![]() , define
, define
Thus, we have
Taking limit in the above equality, by arbitrariness of $\epsilon$![]() , we can obtain
, we can obtain
Moreover, by (2.24) and (2.25), we have

Furthermore, we know that
By (2.28)–(2.30), taking limit $n\to \infty$![]() in (2.27), we have
in (2.27), we have

where
Now, we claim that $z'(t)$![]() has only limited zero points on $[0, T].$
has only limited zero points on $[0, T].$![]() If not, assume that $z'(t)$
If not, assume that $z'(t)$![]() has unlimited zero points $\{\mu _{i}\}_{i\in \mathbb {N}}$
has unlimited zero points $\{\mu _{i}\}_{i\in \mathbb {N}}$![]() on $[0, T].$
on $[0, T].$![]() Without loss of generality, there exists a $\mu _{*}$
Without loss of generality, there exists a $\mu _{*}$![]() such that
such that
Following the continuity of $z'(t)$![]() , we have $z'(\mu _{*})=0$
, we have $z'(\mu _{*})=0$![]() and
and
By the above equality, we can get $z(\mu _{*})\neq 0$![]() . In fact, if $z(\mu _{*})=0$
. In fact, if $z(\mu _{*})=0$![]() , we have
, we have
By choosing a suitable radius $r_{1}$![]() and $r_{2}$
and $r_{2}$![]() such that $\widetilde {t}$
such that $\widetilde {t}$![]() belonging to the left neighbourhood of $(\mu _{*}-r_{1},\mu _{*})$
belonging to the left neighbourhood of $(\mu _{*}-r_{1},\mu _{*})$![]() or the right neighbourhood of $(\mu _{*},\mu _{*}+r_{2})$
or the right neighbourhood of $(\mu _{*},\mu _{*}+r_{2})$![]() , we just need to consider the following four cases.
, we just need to consider the following four cases.

For the case $(C1)$![]() , we can obtain
, we can obtain

which is impossible. For the case $(C2)$![]() , it follows
, it follows

which implies a contradiction. Moreover, by the same way, we can also obtain a contradiction under the case of $(C3)$![]() or $(C4)$
or $(C4)$![]() . Thus, $z(\mu _{*})\neq 0$
. Thus, $z(\mu _{*})\neq 0$![]() . Without loss of generality, assume that $z(\mu _{*})>0$
. Without loss of generality, assume that $z(\mu _{*})>0$![]() . According to its continuity, there exist constants $\xi,\nu >0$
. According to its continuity, there exist constants $\xi,\nu >0$![]() such that
such that
Choosing $n$![]() large enough, we can also get
large enough, we can also get
Since $\mu _{*}$![]() is a limiting point of $\{\mu _{i}\}$
is a limiting point of $\{\mu _{i}\}$![]() , so we can find two zero points called $\mu ^{*},\ \mu ^{**}$
, so we can find two zero points called $\mu ^{*},\ \mu ^{**}$![]() of $z'(t)$
of $z'(t)$![]() in $[\mu _{*}-\nu,\mu _{*}+\nu ]$
in $[\mu _{*}-\nu,\mu _{*}+\nu ]$![]() . Integrating from $\mu ^{*}$
. Integrating from $\mu ^{*}$![]() to $\mu ^{**}$
to $\mu ^{**}$![]() on (2.27), taking limit $n\to \infty$
on (2.27), taking limit $n\to \infty$![]() , we can obtain
, we can obtain

On the other hand, for $t\in [\mu ^{*}, \mu ^{**}]$![]() , choose $n$
, choose $n$![]() large enough such that
large enough such that
Then, we have
Thus, we can obtain

which contradicts to (2.34). Thus, $z'(t)$![]() has only limited zero points on $[0, T].$
has only limited zero points on $[0, T].$![]() Differentiating (2.31), one has
Differentiating (2.31), one has
Since $z'(t)$![]() has only limited zero points on $[0, T]$
has only limited zero points on $[0, T]$![]() , we have
, we have
which together with $\eta \in (0,\infty )\setminus \bigcup _{k=0}^{\infty }[\lambda _{2k}^{min},\lambda _{2k}^{max}]$![]() yield $z(t)\equiv 0$
yield $z(t)\equiv 0$![]() for $t\in [0,T]$
for $t\in [0,T]$![]() . In fact, if there exists a $z\in C_{T}^{1}$
. In fact, if there exists a $z\in C_{T}^{1}$![]() such that (2.36) is satisfied on a subset $\Delta \subset [0,T]$
such that (2.36) is satisfied on a subset $\Delta \subset [0,T]$![]() and $z\equiv 0$
and $z\equiv 0$![]() on $[0,T]\setminus \Delta,$
on $[0,T]\setminus \Delta,$![]() it must be an eigenvector corresponding to a half-eigenvalue, which implies a contradiction. Therefore, $z(t)\equiv 0$
it must be an eigenvector corresponding to a half-eigenvalue, which implies a contradiction. Therefore, $z(t)\equiv 0$![]() . However, it contradicts to $\|z\|_{\infty }=1$
. However, it contradicts to $\|z\|_{\infty }=1$![]() . Thus, there exists a constant $\widetilde {D} >0$
. Thus, there exists a constant $\widetilde {D} >0$![]() which is independent of $\varepsilon _n$
which is independent of $\varepsilon _n$![]() such that $|u_{n}(t)|\leq \widetilde {D}$
such that $|u_{n}(t)|\leq \widetilde {D}$![]() .
.
Since $u_{n}(0)=u_{n}(T)$![]() , there exists $t_{n}\in (0,T)$
, there exists $t_{n}\in (0,T)$![]() such that $u_{n}'(t_{n})=0$
such that $u_{n}'(t_{n})=0$![]() . By the same way to lemma 2.2, we can also get that there exists a constant $\widetilde {K} >0$
. By the same way to lemma 2.2, we can also get that there exists a constant $\widetilde {K} >0$![]() that is independent of $\varepsilon _n$
that is independent of $\varepsilon _n$![]() such that $|u'_{n}(t)|\leq \widetilde {K}$
such that $|u'_{n}(t)|\leq \widetilde {K}$![]() . By Arzelá–Ascoli theorem (without loss of generality, take its subsequence), there exist $u\in C_{T}^{1}$
. By Arzelá–Ascoli theorem (without loss of generality, take its subsequence), there exist $u\in C_{T}^{1}$![]() and $t_{0}\in [0,T]$
and $t_{0}\in [0,T]$![]() such that $\mathop {\lim }\limits _{n \to \infty } t_n = t_{0}$
such that $\mathop {\lim }\limits _{n \to \infty } t_n = t_{0}$![]() ,
,
Taking limit $n\to \infty$![]() in the following equation
in the following equation
we have
which implies that for all $t\in [0,T]$![]()
and $u(0) = u(T),u'(0) = u'(T).$![]() Thus, the problem (1.1) has at least one periodic solution.
Thus, the problem (1.1) has at least one periodic solution.
Remark 2.7 It should be mentioned that in the separated boundary conditions, typical existence results in this area usually assume that $\eta$![]() lies in the gap between half-eigenvalues with consecutive nodal counts, not between half-eigenvalues with the same nodal counts that may make the problem not have a solution (see [Reference Rynne23, Reference Rynne24]).
lies in the gap between half-eigenvalues with consecutive nodal counts, not between half-eigenvalues with the same nodal counts that may make the problem not have a solution (see [Reference Rynne23, Reference Rynne24]).
Theorem 2.8 For $1< p<\infty,$![]() if $(H3),$
if $(H3),$![]() $(H5)$
$(H5)$![]() and $(H6)$
and $(H6)$![]() hold. Then the problem (1.2) has at least one periodic solutions.
hold. Then the problem (1.2) has at least one periodic solutions.
Proof. Based on lemma 2.4, by similar way to theorem 2.6, the conclusion of theorem 2.8 is also true. Here, we omit the detail.
Remark 2.9 If $\overline {g}_{1}=0$![]() , $a_{\pm }$
, $a_{\pm }$![]() are positive constants and $\widetilde {{g}}_{0}(u)$
are positive constants and $\widetilde {{g}}_{0}(u)$![]() satisfies $(H5)$
satisfies $(H5)$![]() and $\mathop {\lim }\limits _{|u| \to \infty } \frac {{pG_{0}(u)}}{{|u|^{p} }} = \eta$
and $\mathop {\lim }\limits _{|u| \to \infty } \frac {{pG_{0}(u)}}{{|u|^{p} }} = \eta$![]() , letting
, letting
by theorem 2.8, the problem (1.2) has at least one periodic solutions, provided that $(a_{+}+\eta,a_{-}+\eta )\notin S_{p},$![]() which is corresponding to theorem 2.3 of [Reference Liu and Li17]. Thus, our main results generalize their conclusions.
which is corresponding to theorem 2.3 of [Reference Liu and Li17]. Thus, our main results generalize their conclusions.
Acknowledgements
The authors are grateful to the referees for a careful and thorough reading of this paper and also for their valuable suggestions and comments, which improved the former version of this paper.
Supported by the Natural Science Foundation of Jiangsu Province, China (No. BK20190620).