We elaborate on the construction of the Evans chain complex for higher-rank graph $C^*$-algebras. Specifically, we introduce a block matrix presentation of the differential maps. These block matrices are then used to identify a wide family of higher-rank graph $C^*$-algebras with trivial K-theory. Additionally, in the specialised case where the higher-rank graph consists of one vertex, we are able to use the Künneth theorem to explicitly compute the homology groups of the Evans chain complex.

In this work, we explore the dynamical implications of a spectral sequence analysis of a filtered chain complex associated to a non-singular Morse–Smale (NMS) flow $\varphi $ on a closed orientable $3$-manifold $M^3$ with no heteroclinic trajectories connecting saddle periodic orbits. We introduce the novel concepts of cancellations and reductions of pairs of periodic orbits based on Franks’ morsification and Smale’s cancellation theorems. The main goal is to establish an algebraic-dynamical correspondence between the unfolding of this spectral sequence associated to $\varphi $ and a family of flows obtained by cancelling and reducing pairs of periodic orbits of $\varphi $ on $M^3$. This correspondence is achieved through a spectral sequence sweeping algorithm (SSSA), which determines the order in which these cancellations and reductions of periodic orbits occur, producing a family of NMS flows that reaches a core flow when the spectral sequence converges.

The Jones polynomial is a famous link invariant that can be defined diagrammatically via a skein relation. Khovanov homology is a richer link invariant that categorifies the Jones polynomial. Using spectral sequences, we obtain a skein-type relation satisfied by the Khovanov homology. Thanks to this relation, we are able to generalize the Khovanov homology in order to obtain a categorification of the θ-invariant, which is itself a generalization of the Jones polynomial.

Suppose that B is a G-Banach algebra over 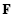= ℝ or ℂ X is a finite dimensional compact metric space, ζ : P → X is a standard principal G-bundle, and Aζ = Γ(X,P ×GB) is the associated algebra of sections. We produce a spectral sequence which converges to π*(GLoAζ) with

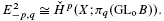
A related spectral sequence converging to K*+1(Aζ) (the real or complex topological K-theory) allows us to conclude that if B is Bott-stable, (i.e., if π*(GLoB) → K*+1(B) is an isomorphism for all * > 0) then so is Aζ.

Felix and Murillo introduced the group $\mathrm{Aut}_\varOmega(X)$ of self-maps $f$ of $X$, which satisfy $\sOm f=1_{\varOmega X}$, and proved that the group is nilpotent with the order of nilpotency bounded by the Lusternik–Schnirelmann category of $X$. In this paper we construct a spectral sequence converging to the group $\mathrm{Aut}_\varOmega(X)$ and derive several interesting consequences.

AMS 2000 Mathematics subject classification: Primary 55P42