In this paper we study a variation of the random $k$-SAT problem, called polarised random $k$-SAT, which contains both the classical random 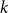$k$-SAT model and the random version of monotone $k$-SAT another well-known NP-complete version of SAT. In this model there is a polarisation parameter 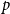$p$, and in half of the clauses each variable occurs negated with probability 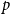$p$ and pure otherwise, while in the other half the probabilities are interchanged. For $p=1/2$ we get the classical random 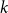$k$-SAT model, and at the other extreme we have the fully polarised model where 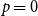$p=0$, or 1. Here there are only two types of clauses: clauses where all $k$ variables occur pure, and clauses where all 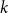$k$ variables occur negated. That is, for $p=0$, and 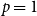$p=1$, we get an instance of random monotone $k$-SAT.

We show that the threshold of satisfiability does not decrease as 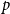$p$ moves away from $\frac{1}{2}$ and thus that the satisfiability threshold for polarised random 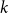$k$-SAT with $p\neq \frac{1}{2}$ is an upper bound on the threshold for random 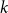$k$-SAT. Hence the satisfiability threshold for random monotone 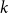$k$-SAT is at least as large as for random $k$-SAT, and we conjecture that asymptotically, for a fixed 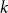$k$, the two thresholds coincide.

The decoupling between the representation of a certain problem, that is, its knowledge model, and the reasoning side is one of main strong points of model-based artificial intelligence (AI). This allows, for example, to focus on improving the reasoning side by having advantages on the whole solving process. Further, it is also well known that many solvers are very sensitive to even syntactic changes in the input. In this paper, we focus on improving the reasoning side by taking advantages of such sensitivity. We consider two well-known model-based AI methodologies, SAT and ASP, define a number of syntactic features that may characterise their inputs, and use automated configuration tools to reformulate the input formula or program. Results of a wide experimental analysis involving SAT and ASP domains, taken from respective competitions, show the different advantages that can be obtained by using input reformulation and configuration.

A complete classification of the complexity of the local and global satisfiability problems for graded modal language over traditional classes of frames has already been established. By “traditional” classes of frames, we mean those characterized by any positive combination of reflexivity, seriality, symmetry, transitivity, and the Euclidean property. In this paper, we fill the gaps remaining in an analogous classification of the graded modal language with graded converse modalities. In particular, we show its NExpTime-completeness over the class of Euclidean frames, demonstrating this way that over this class the considered language is harder than the language without graded modalities or without converse modalities. We also consider its variation disallowing graded converse modalities, but still admitting basic converse modalities. Our most important result for this variation is confirming an earlier conjecture that it is decidable over transitive frames. This contrasts with the undecidability of the language with graded converse modalities.

We study the fluted fragment, a decidable fragment of first-order logic with an unbounded number of variables, motivated by the work of W. V. Quine. We show that the satisfiability problem for this fragment has nonelementary complexity, thus refuting an earlier published claim by W. C. Purdy that it is in NExpTime. More precisely, we consider ${\cal F}{{\cal L}^m}$, the intersection of the fluted fragment and the m-variable fragment of first-order logic, for all $m \ge 1$. We show that, for $m \ge 2$, this subfragment forces $\left\lfloor {m/2} \right\rfloor$-tuply exponentially large models, and that its satisfiability problem is $\left\lfloor {m/2} \right\rfloor$-NExpTime-hard. We further establish that, for $m \ge 3$, any satisfiable ${\cal F}{{\cal L}^m}$-formula has a model of at most ($m - 2$)-tuply exponential size, whence the satisfiability (= finite satisfiability) problem for this fragment is in ($m - 2$)-NExpTime. Together with other, known, complexity results, this provides tight complexity bounds for ${\cal F}{{\cal L}^m}$ for all $m \le 4$.

As proved recently, the satisfaction problem for all prenex formulae in the set-theoretic Bernays-Shönfinkel-Ramsey class is semi-decidable over von Neumann's cumulative hierarchy. Here that semi-decidability result is strengthened into a decidability result for the same collection of formulae.

It is well known that, as n tends to ∞, the probability of satisfiability for a random 2-SAT formula on n variables, where each clause occurs independently with probability α / 2n, exhibits a sharp threshold at α = 1. We study a more general 2-SAT model in which each clause occurs independently but with probability αi / 2n, where i ∈ {0, 1, 2} is the number of positive literals in that clause. We generalize the branching process arguments used by Verhoeven (1999) to determine the satisfiability threshold for this model in terms of the maximum eigenvalue of the branching matrix.

As is well-known, the Bernays-Schönfinkel-Ramsey class of all prenex ∃*∀*-sentences which are valid in classical first-order logic is decidable. This paper paves the way to an analogous result which the authors deem to hold when the only available predicate symbols are ∈ and =, no constants or function symbols are present, and one moves inside a (rather generic) Set Theory whose axioms yield the well-foundedness of membership and the existence of infinite sets. Here semi-decidability of the satisfiability problem for the BSR class is proved by following a purely semantic approach, the remaining part of the decidability result being postponed to a forthcoming paper.

The aim of this paper is to study the threshold behavior for the satisfiability property of a random k-XOR-CNF formula or equivalently for the consistency of a random Boolean linear system with k variables per equation. For k ≥ 3 we show the existence of a sharp threshold for the satisfiability of a random k-XOR-CNF formula, whereas there are smooth thresholds for k=1 and k=2.

This article addresses computational synthesis systems that attempt to find a structural description that matches a set of initial functional requirements and design constraints with a finite sequence of production rules. It has been previously shown by the author that it is computationally difficult to identify a sequence of production rules that can lead to a satisficing design solution. As a result, computational synthesis, particularly with large volumes of selection information, requires effective design search procedures. Many computational synthesis systems utilize transformational search strategies. However, such search strategies are inefficient due to the combinatorial nature of the problem. In this article, the problem is approached using a completely different paradigm. The new approach encodes a design search problem as a Boolean (propositional) satisfiability problem, such that from every satisfying Boolean-valued truth assignment to the corresponding Boolean expression we efficiently can derive a solution to the original synthesis problem (along with its finite sequence of production rules). A major advantage of the proposed approach is the possibility of utilizing recently developed powerful randomized search algorithms for solving Boolean satisfiability problems, which considerably outperform the most widely used satisfiability algorithms. The new design-as-satisfiability technique provides a flexible framework for stating a variety of design constraints, and also represents properly the theory behind modern constraint-based design systems.