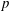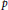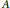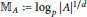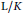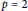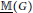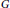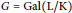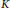For a finite abelian 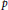 $p$-group
$p$-group 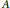 $A$ of rank
$A$ of rank  $d\,=\,\dim\,A/pA$, let
$d\,=\,\dim\,A/pA$, let 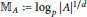 ${{\mathbb{M}}_{A}}\,:=\,\text{lo}{{\text{g}}_{p}}\,{{\left| A \right|}^{1/d}}$ be its (logarithmic) mean exponent. We study the behavior of the mean exponent of
${{\mathbb{M}}_{A}}\,:=\,\text{lo}{{\text{g}}_{p}}\,{{\left| A \right|}^{1/d}}$ be its (logarithmic) mean exponent. We study the behavior of the mean exponent of 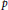 $p$-class groups in pro-
$p$-class groups in pro-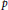 $p$ towers
$p$ towers 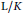 $\text{L/K}$ of number fields. Via a combination of results from analytic and algebraic number theory, we construct infinite tamely ramified pro-
$\text{L/K}$ of number fields. Via a combination of results from analytic and algebraic number theory, we construct infinite tamely ramified pro-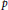 $p$ towers in which the mean exponent of
$p$ towers in which the mean exponent of 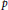 $p$-class groups remains bounded. Several explicit examples are given with
$p$-class groups remains bounded. Several explicit examples are given with 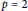 $p\,=\,2$. Turning to group theory, we introduce an invariant
$p\,=\,2$. Turning to group theory, we introduce an invariant 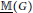 $\underline{\mathbb{M}}\left( G \right)$ attached to a finitely generated pro-
$\underline{\mathbb{M}}\left( G \right)$ attached to a finitely generated pro-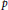 $p$ group
$p$ group 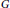 $G$; when
$G$; when 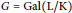 $G\,=\,\text{Gal}\left( \text{L/K} \right)$, where
$G\,=\,\text{Gal}\left( \text{L/K} \right)$, where  $L$ is the Hilbert
$L$ is the Hilbert 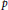 $p$-class field tower of a number field
$p$-class field tower of a number field 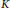 $K$,
$K$, 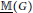 $\underline{\mathbb{M}}\left( G \right)$ measures the asymptotic behavior of the mean exponent of
$\underline{\mathbb{M}}\left( G \right)$ measures the asymptotic behavior of the mean exponent of 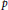 $p$-class groups inside
$p$-class groups inside 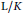 $\text{L/K}$. We compare and contrast the behavior of this invariant in analytic versus non-analytic groups. We exploit the interplay of group-theoretical and number-theoretical perspectives on this invariant and explore some open questions that arise as a result, which may be of independent interest in group theory.
$\text{L/K}$. We compare and contrast the behavior of this invariant in analytic versus non-analytic groups. We exploit the interplay of group-theoretical and number-theoretical perspectives on this invariant and explore some open questions that arise as a result, which may be of independent interest in group theory.
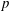 $p$ Groups
$p$ Groups