We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The $q$
-coloured Delannoy numbers $D_{n,k}(q)$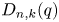
count the number of lattice paths from $(0,\,0)$
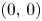to $(n,\,k)$
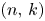using steps $(0,\,1)$
, $(1,\,0)$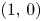
and $(1,\,1)$
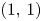, among which the $(1,\,1)$
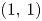steps are coloured with $q$
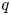colours. The focus of this paper is to study some analytical properties of the polynomial matrix $D(q)=[d_{n,k}(q)]_{n,k\geq 0}=[D_{n-k,k}(q)]_{n,k\geq 0}$
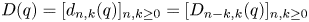, such as the strong $q$
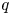-log-concavity of polynomial sequences located in a ray or a transversal line of $D(q)$
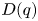and the $q$
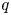-total positivity of $D(q)$
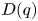. We show that the zeros of all row sums $R_n(q)=\sum \nolimits _{k=0}^{n}d_{n,k}(q)$
are in $(-\infty,\, -1)$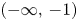
and are dense in the corresponding semi-closed interval. We also prove that the zeros of all antidiagonal sums $A_n(q)=\sum \nolimits _{k=0}^{\lfloor n/2 \rfloor }d_{n-k,k}(q)$
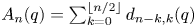are in the interval $(-\infty,\, -1]$
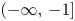and are dense there.
