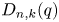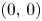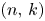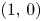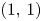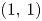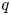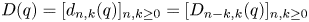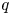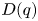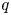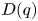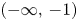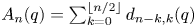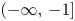1. Introduction
Delannoy numbers correspond to the number of paths from $(0,\,0)$![]() to $(n,\,k)$
to $(n,\,k)$![]() , with jumps $(0,\,1)$
, with jumps $(0,\,1)$![]() , $(1,\,1)$
, $(1,\,1)$![]() , or $(1,\,0)$
, or $(1,\,0)$![]() , which we denote by the sequence $(D_{n,k})_{n,k\in N}$
, which we denote by the sequence $(D_{n,k})_{n,k\in N}$![]() . Then a recurrence follows that
. Then a recurrence follows that
or a further expression

For the historic and academic backgrounds of Delannoy numbers, and the biography of Henri Delannoy, we refer the reader to [Reference Banderier and Schwer1] and the bibliographic references therein. There have been a lot of research interests in Delannoy numbers for their nice properties. For instance, a recent work is dedicated to their analytic properties [Reference Wang, Zheng and Chen21].
In particular, when $n=k$![]() , $D(n,\,n)$
, $D(n,\,n)$![]() denotes the central Delannoy numbers. We refer the reader to [Reference Banderier and Schwer1, Reference Sulanke16] for their combinatorial properties [Reference Sun17, Reference Sun18], for their work on certain number-theoretic properties [Reference Torres, Cabada and Nieto19], for their biological applications in the alignments between DNA sequences, etc.
denotes the central Delannoy numbers. We refer the reader to [Reference Banderier and Schwer1, Reference Sulanke16] for their combinatorial properties [Reference Sun17, Reference Sun18], for their work on certain number-theoretic properties [Reference Torres, Cabada and Nieto19], for their biological applications in the alignments between DNA sequences, etc.
If all the $(1,\,1)$![]() steps, i.e. the diagonal ones, of a Delannoy path are coloured with $q$
steps, i.e. the diagonal ones, of a Delannoy path are coloured with $q$![]() colours $(q \geq 0)$
colours $(q \geq 0)$![]() , then we call it $q$
, then we call it $q$![]() -coloured Delannoy path. Let $D_{n,k}(q)$
-coloured Delannoy path. Let $D_{n,k}(q)$![]() denote the number of $q$
denote the number of $q$![]() -coloured Delannoy paths from $(0,\,0)$
-coloured Delannoy paths from $(0,\,0)$![]() to $(n,\,k)$
to $(n,\,k)$![]() in this case. Then, analogous to (1.1) and (1.2), respectively, we have
in this case. Then, analogous to (1.1) and (1.2), respectively, we have
and

As a polynomial, $D_{n,k}(q)$![]() has some nice properties, which is partly due to the fact that it is both a Gaussian hypergeometric function $_{2}F_{1}(-n,\,-k;1;q+1)$
has some nice properties, which is partly due to the fact that it is both a Gaussian hypergeometric function $_{2}F_{1}(-n,\,-k;1;q+1)$![]() and a special Jacobi polynomial $P_n^{(0,-n-k-1)}(-2q-1)$
and a special Jacobi polynomial $P_n^{(0,-n-k-1)}(-2q-1)$![]() . $D_{n,k}(q)$
. $D_{n,k}(q)$![]() also appears in chemical graph theory, as the Clar covering polynomial of one kind of hexagonal systems [Reference Gutman and Borovićanin7]. Moreover, $D_{n,k}(q)$
also appears in chemical graph theory, as the Clar covering polynomial of one kind of hexagonal systems [Reference Gutman and Borovićanin7]. Moreover, $D_{n,k}(q)$![]() can be proved to have only real zeros by the Maló Theorem [Reference Maló10], which states that if both $\sum \nolimits _{i=0}^{n}a_iq^{i}$
can be proved to have only real zeros by the Maló Theorem [Reference Maló10], which states that if both $\sum \nolimits _{i=0}^{n}a_iq^{i}$![]() and $\sum \nolimits _{j=0}^{m}b_jq^{j}$
and $\sum \nolimits _{j=0}^{m}b_jq^{j}$![]() have only real zeros then $\sum \nolimits _{k=0}^{min\{n,m\}}a_kb_kq^{k}$
have only real zeros then $\sum \nolimits _{k=0}^{min\{n,m\}}a_kb_kq^{k}$![]() has only real zeros. It is also worth noting that many well-known combinatorial counting sequences are $q$
has only real zeros. It is also worth noting that many well-known combinatorial counting sequences are $q$![]() -coloured Delannoy numbers. For example, $D_{n,k}(0)$
-coloured Delannoy numbers. For example, $D_{n,k}(0)$![]() are the binomial coefficients and $D_{n,k}(1)$
are the binomial coefficients and $D_{n,k}(1)$![]() are the Delannoy numbers [Reference Banderier and Schwer1]. In a sense, that endowing the diagonal steps with being $q$
are the Delannoy numbers [Reference Banderier and Schwer1]. In a sense, that endowing the diagonal steps with being $q$![]() -coloured pleasantly brings more research materials to the existing setting. Our paper is to study some analytical properties of the matrix related to $q$
-coloured pleasantly brings more research materials to the existing setting. Our paper is to study some analytical properties of the matrix related to $q$![]() -coloured Delannoy numbers.
-coloured Delannoy numbers.
The $q$![]() -coloured Delannoy numbers constitute the square matrix
-coloured Delannoy numbers constitute the square matrix

whereas our paper focuses on the following triangular matrix

which is derived by arranging the $q$![]() -coloured Delannoy numbers in a triangle array, i.e. $d_{n,k}(q)=D_{n-k,k}(q)$
-coloured Delannoy numbers in a triangle array, i.e. $d_{n,k}(q)=D_{n-k,k}(q)$![]() . This matrix is more convenient for the following investigation than the former one (albeit more natural), and therefore is our protagonist here. It is interesting to mention in passing that $D(q)$
. This matrix is more convenient for the following investigation than the former one (albeit more natural), and therefore is our protagonist here. It is interesting to mention in passing that $D(q)$![]() can unify some combinatorial triangles. For example, $D(0)$
can unify some combinatorial triangles. For example, $D(0)$![]() is the well-known Pascal triangle, $D(1)$
is the well-known Pascal triangle, $D(1)$![]() is the Delannoy triangle [Reference Wang, Zheng and Chen21, Reference Yang, Zheng, Yuan and He25], $D(2)$
is the Delannoy triangle [Reference Wang, Zheng and Chen21, Reference Yang, Zheng, Yuan and He25], $D(2)$![]() and $D(3)$
and $D(3)$![]() also could be found in [Reference Barry2] and [Reference Sloane14, A081577, A081578].
also could be found in [Reference Barry2] and [Reference Sloane14, A081577, A081578].
The paper is organized as follows. In the next section, we show that the polynomial sequences located in a ray or a transversal line of $D(q)$![]() are strongly $q$
are strongly $q$![]() -log-concave. Section 3 proves that $D(q)$
-log-concave. Section 3 proves that $D(q)$![]() is $q$
is $q$![]() -totally positive. In § 4, we first show, for the row sums $R_n(q)$
-totally positive. In § 4, we first show, for the row sums $R_n(q)$![]() , that all their zeros lie in the open interval $(-\infty,\, -1)$
, that all their zeros lie in the open interval $(-\infty,\, -1)$![]() and are dense in the semi-closed interval $(-\infty,\, -1]$
and are dense in the semi-closed interval $(-\infty,\, -1]$![]() . And then, for the antidiagonal sums $A_n(q)$
. And then, for the antidiagonal sums $A_n(q)$![]() , we show that all zeros are in the interval $(-\infty,\, -1]$
, we show that all zeros are in the interval $(-\infty,\, -1]$![]() and are dense there. At the end of this paper, we finish with a remark that the coefficients $r_{n,i}$
and are dense there. At the end of this paper, we finish with a remark that the coefficients $r_{n,i}$![]() are asymptotically normal by central and local limit theorems.
are asymptotically normal by central and local limit theorems.
2. Strong $q$ -log-concavity of $D(q)$
-log-concavity of $D(q)$
Let $f(q)$![]() and $g(q)$
and $g(q)$![]() be two real polynomials in $q$
be two real polynomials in $q$![]() . We say that $f(q)$
. We say that $f(q)$![]() is $q$
is $q$![]() -non-negative if $f(q)$
-non-negative if $f(q)$![]() has non-negative coefficients. Denote $f(q)\geq _q g(q)$
has non-negative coefficients. Denote $f(q)\geq _q g(q)$![]() if the difference $f(q)-g(q)$
if the difference $f(q)-g(q)$![]() is $q$
is $q$![]() -non-negative. For a polynomial sequence $(f_n(q))_{n\geq 0}$
-non-negative. For a polynomial sequence $(f_n(q))_{n\geq 0}$![]() , it is called $q$
, it is called $q$![]() -log-concave (or $q$
-log-concave (or $q$![]() -log-convex) if
-log-convex) if
for $n \geq 1$![]() . It is called strongly $q$
. It is called strongly $q$![]() -log-concave (or strongly $q$
-log-concave (or strongly $q$![]() -log-convex) if
-log-convex) if
for $n \geq m \geq 1$![]() . Clearly, the strong $q$
. Clearly, the strong $q$![]() -log-concavity (strong $q$
-log-concavity (strong $q$![]() -log-convexity) of polynomial sequences implies the $q$
-log-convexity) of polynomial sequences implies the $q$![]() -log-concavity ($q$
-log-concavity ($q$![]() -log-convexity), which further implies the log-concavity (log-convexity) for any fixed $q \geq 0$
-log-convexity), which further implies the log-concavity (log-convexity) for any fixed $q \geq 0$![]() , however, not vice versa. The (strong) $q$
, however, not vice versa. The (strong) $q$![]() -log-concavity has been extensively studied; see [Reference Butler5, Reference Leroux8, Reference Sagan13].
-log-concavity has been extensively studied; see [Reference Butler5, Reference Leroux8, Reference Sagan13].
It is known that $D(0)$![]() is the Pascal triangle $P$
is the Pascal triangle $P$![]() . Su and Wang [Reference Su and Wang15] proved the log-concavity of the sequence located in a transversal line of $P$
. Su and Wang [Reference Su and Wang15] proved the log-concavity of the sequence located in a transversal line of $P$![]() or a line parallel to the boundary of $P$
or a line parallel to the boundary of $P$![]() . Yu [Reference Yu24] pointed out that such properties also hold in $D(1)$
. Yu [Reference Yu24] pointed out that such properties also hold in $D(1)$![]() which is the Delannoy triangle.
which is the Delannoy triangle.
The central coefficients $d_{2n,n}(q)$![]() of $D(q)$
of $D(q)$![]() are $q$
are $q$![]() -central Delannoy numbers
-central Delannoy numbers

Liu and Wang [Reference Liu and Wang9] proved that the sequence of $q$![]() -central Delannoy numbers $(D_n(q))_{n\geq 0}$
-central Delannoy numbers $(D_n(q))_{n\geq 0}$![]() is $q$
is $q$![]() -log-convex. Zhu [Reference Zhu26, Reference Zhu27] later proved that $(D_n(q))_{n\geq 0}$
-log-convex. Zhu [Reference Zhu26, Reference Zhu27] later proved that $(D_n(q))_{n\geq 0}$![]() is strongly $q$
is strongly $q$![]() -log-convex. Wang and Zhu [Reference Wang and Zhu23] gave a stronger result that $(D_n(q))_{n\geq 0}$
-log-convex. Wang and Zhu [Reference Wang and Zhu23] gave a stronger result that $(D_n(q))_{n\geq 0}$![]() forms a $q$
forms a $q$![]() -Stieltjes moment sequence, i.e., all minors of the corresponding Hankel matrix $[D_{i+j}(q)]$
-Stieltjes moment sequence, i.e., all minors of the corresponding Hankel matrix $[D_{i+j}(q)]$![]() are $q$
are $q$![]() -non-negative.
-non-negative.
In this section, we aim to study the strong $q$![]() -log-concavity of a polynomial sequence located in a ray or a transversal line of $D(q)$
-log-concavity of a polynomial sequence located in a ray or a transversal line of $D(q)$![]() . Let $(d_{n_i,k_i}(q))_{i\geq 0}$
. Let $(d_{n_i,k_i}(q))_{i\geq 0}$![]() be such a sequence. Then $(n_i)_{i\geq 0}$
be such a sequence. Then $(n_i)_{i\geq 0}$![]() and $(k_i)_{i\geq 0}$
and $(k_i)_{i\geq 0}$![]() form two arithmetic sequences (see Figure 1). Clearly, the common difference of $(n_i)_{i\geq 0}$
form two arithmetic sequences (see Figure 1). Clearly, the common difference of $(n_i)_{i\geq 0}$![]() can be assumed to be non-negative. Meanwhile the common difference of $(k_i)_{i\geq 0}$
can be assumed to be non-negative. Meanwhile the common difference of $(k_i)_{i\geq 0}$![]() can also be assumed to be non-negative without loss of generality since the symmetry of $D(q)$
can also be assumed to be non-negative without loss of generality since the symmetry of $D(q)$![]() leads to the fact that the sequences $(d_{n_i,k_i}(q))_{i\geq 0}$
leads to the fact that the sequences $(d_{n_i,k_i}(q))_{i\geq 0}$![]() and $(d_{n_i,n_i-k_i}(q))_{i\geq 0}$
and $(d_{n_i,n_i-k_i}(q))_{i\geq 0}$![]() are the same. Thus, to achieve our aim, it suffices to investigate the strong $q$
are the same. Thus, to achieve our aim, it suffices to investigate the strong $q$![]() -log-concavity of the sequence $(d_{n_0+ai,k_0+bi}(q))_{i\geq 0}$
-log-concavity of the sequence $(d_{n_0+ai,k_0+bi}(q))_{i\geq 0}$![]() for non-negative integers $a$
for non-negative integers $a$![]() and $b$
and $b$![]() , giving rise to our first main result of this paper.
, giving rise to our first main result of this paper.
Theorem 2.1 Let $n_0,$![]() $k_0,$
$k_0,$![]() $a$
$a$![]() and $b$
and $b$![]() be four non-negative integers and $n_0\geq k_0,$
be four non-negative integers and $n_0\geq k_0,$![]() $a+b\neq 0$
$a+b\neq 0$![]() . Define the sequence
. Define the sequence
If $a\leq b,$![]() then the polynomial sequence $(S_i(q))_{i\geq 0}$
then the polynomial sequence $(S_i(q))_{i\geq 0}$![]() is strongly $q$
is strongly $q$![]() -log-concave.
-log-concave.

Figure 1. The symmetric isosceles triangle $D(q)$![]() of $q$
of $q$![]() -coloured Delannoy numbers.
-coloured Delannoy numbers.
Before a combinatorial proof of this theorem, we need to introduce a few notions. Let $\mathfrak {D}(n,\,k)$![]() denote the set of all $q$
denote the set of all $q$![]() -coloured Delannoy paths from $(s,\,t)$
-coloured Delannoy paths from $(s,\,t)$![]() to $(s+n,\,t+k)$
to $(s+n,\,t+k)$![]() for fixed $s$
for fixed $s$![]() and $t$
and $t$![]() . Note that $S_i(q)$
. Note that $S_i(q)$![]() count the number of $q$
count the number of $q$![]() -coloured Delannoy paths from $(0,\,0)$
-coloured Delannoy paths from $(0,\,0)$![]() to $(n_0-k_0+(a-b)i,\,k_0+bi)$
to $(n_0-k_0+(a-b)i,\,k_0+bi)$![]() . Hence, for convenience we let
. Hence, for convenience we let
Then we have
where the weight of path $P$![]() , denoted by $w(P)$
, denoted by $w(P)$![]() , is defined as the product of the weights of all its steps. Suppose that $P$
, is defined as the product of the weights of all its steps. Suppose that $P$![]() has exactly $k$
has exactly $k$![]() diagonal steps (i.e. $(1,\,1)$
diagonal steps (i.e. $(1,\,1)$![]() steps). Then
steps). Then
since the weight of each diagonal step in P is $q$![]() , and the others $1$
, and the others $1$![]() . Moreover, $w(P,\,Q)=w(P)w(Q)$
. Moreover, $w(P,\,Q)=w(P)w(Q)$![]() is to denote the weight of a pair of $q$
is to denote the weight of a pair of $q$![]() -coloured Delannoy paths in the following.
-coloured Delannoy paths in the following.
Proof of Theorem 2.1 To show the strong $q$![]() -log-concavity of $(S_i(q))_{i\geq 0}$
-log-concavity of $(S_i(q))_{i\geq 0}$![]() , it suffices to show that
, it suffices to show that
for $i\geq j$![]() , i.e.,
, i.e.,
It is equivalent to
Let $N_k(\mathfrak {D}_i,\,\mathfrak {D}_j)$![]() denote the number of pairs of paths with exactly $k$
denote the number of pairs of paths with exactly $k$![]() diagonal steps in the set $(\mathfrak {D}_i,\,\mathfrak {D}_j)$
diagonal steps in the set $(\mathfrak {D}_i,\,\mathfrak {D}_j)$![]() . So it needs to prove
. So it needs to prove
To this end, we construct an injection from $(\mathfrak {D}_{i+1},\,\mathfrak {D}_{j-1})$![]() to $(\mathfrak {D}_i,\,\mathfrak {D}_j)$
to $(\mathfrak {D}_i,\,\mathfrak {D}_j)$![]() , i.e.,
, i.e.,
such that
Each pair of $(P_1,\,P_2)$![]() in $(\mathfrak {D}_{i+1},\,\mathfrak {D}_{j-1})$
in $(\mathfrak {D}_{i+1},\,\mathfrak {D}_{j-1})$![]() , as shown in Figure 2, follows such rules:
, as shown in Figure 2, follows such rules:
P1: $(0,\,0)\rightarrow (n_0-k_0+(a-b)(i+1),\,k_0+b(i+1))$
 ;
;P2: $((a-b)(i-j+1),\,b(i-j+1))\rightarrow (n_0-k_0+(a-b)i,\,k_0+bi)$
 .
.
Clearly, $P_1$![]() and $P_2$
and $P_2$![]() must intersect at least one lattice point in the shadow area. Let $A$
must intersect at least one lattice point in the shadow area. Let $A$![]() denote the first intersection point. Then we define the operation $\phi$
denote the first intersection point. Then we define the operation $\phi$![]() on $(P_1,\,P_2)$
on $(P_1,\,P_2)$![]() at the point $A$
at the point $A$![]() :
:
“Switch the initial segments of the two paths”,
as shown in Figure 3. With this operation $\phi$![]() , we could obtain a corresponding pair $(Q_1,\,Q_2)\in (\mathfrak {D}_i,\,\mathfrak {D}_j)$
, we could obtain a corresponding pair $(Q_1,\,Q_2)\in (\mathfrak {D}_i,\,\mathfrak {D}_j)$![]() , and
, and
Q1: $((a-b)(i-j+1),\,b(i-j+1))\rightarrow (n_0-k_0+(a-b)(i+1),\,k_0+b(i+1))$
 ;
;Q2: $(0,\,0)\rightarrow (n_0-k_0+(a-b)i,\,k_0+bi)$
 .
.

Figure 2. $(P_1,\,P_2)\in (\mathfrak {D}_{i+1},\,\mathfrak {D}_{j-1})$![]() .
.

Figure 3. Operation $\phi$![]() on $(P_1,\,P_2)$
on $(P_1,\,P_2)$![]() in Figure 2.
in Figure 2.
For instance, let $n_0=10$![]() , $k_0=3$
, $k_0=3$![]() , $a=0$
, $a=0$![]() and $b=1$
and $b=1$![]() , and take $i=2$
, and take $i=2$![]() , $j=1$
, $j=1$![]() . Then $(P_1,\,P_2)\in (\mathfrak {D}_{3},\,\mathfrak {D}_{0})$
. Then $(P_1,\,P_2)\in (\mathfrak {D}_{3},\,\mathfrak {D}_{0})$![]() , where $P_1$
, where $P_1$![]() goes from $(0,\,0)$
goes from $(0,\,0)$![]() to $(4,\,6)$
to $(4,\,6)$![]() and $P_2$
and $P_2$![]() from $(-2,\,2)$
from $(-2,\,2)$![]() to $(5,\,5)$
to $(5,\,5)$![]() , as shown in Figure 4. The operation $\phi$
, as shown in Figure 4. The operation $\phi$![]() on $(P_1,\,P_2)\in (\mathfrak {D}_{3},\,\mathfrak {D}_{0})$
on $(P_1,\,P_2)\in (\mathfrak {D}_{3},\,\mathfrak {D}_{0})$![]() at the point $A$
at the point $A$![]() will lead to a pair $(Q_1,\,Q_2)\in (\mathfrak {D}_{2},\,\mathfrak {D}_{1})$
will lead to a pair $(Q_1,\,Q_2)\in (\mathfrak {D}_{2},\,\mathfrak {D}_{1})$![]() as shown in Figure 4.
as shown in Figure 4.

Figure 4. $(P_1,\,P_2)\in (\mathfrak {D}_{3},\,\mathfrak {D}_{0})\rightarrow (Q_1,\,Q_2)\in (\mathfrak {D}_{2},\,\mathfrak {D}_{1})$![]() .
.
Note that the location of the first intersection point remains invariant under the operation $\phi$![]() , which means $\phi$
, which means $\phi$![]() is invertible and so that it is an injection. Meanwhile, it is easy to check that the number of diagonal steps also remains invariant under the injection $\phi$
is invertible and so that it is an injection. Meanwhile, it is easy to check that the number of diagonal steps also remains invariant under the injection $\phi$![]() , i.e., the number of diagonal steps in $(P_1,\,P_2)$
, i.e., the number of diagonal steps in $(P_1,\,P_2)$![]() is the same as that in $(Q_1,\,Q_2)$
is the same as that in $(Q_1,\,Q_2)$![]() . Therefore, (2.4) follows, by which (2.1) can be obtained as desired.
. Therefore, (2.4) follows, by which (2.1) can be obtained as desired.
From Theorem 2.1, we have the following corollary immediately.
Corollary 2.2 All the polynomial sequences located in a transversal of $D(q)$![]() or in a line parallel to the boundary of $D(q)$
or in a line parallel to the boundary of $D(q)$![]() are strongly $q$
are strongly $q$![]() -log-concave.
-log-concave.
Note that $D(0)$![]() and $D(1)$
and $D(1)$![]() are Pascal triangle and Delannoy triangle, respectively. The log-concavity of the sequences in these two triangles was mentioned at the beginning of this section. $D(2)$
are Pascal triangle and Delannoy triangle, respectively. The log-concavity of the sequences in these two triangles was mentioned at the beginning of this section. $D(2)$![]() and $D(3)$
and $D(3)$![]() are also Pascal-like triangles and could be found in [Reference Sloane14, A081577, A081578]. By Theorem 2.1, we can get the log-concavity of sequences in these two triangles.
are also Pascal-like triangles and could be found in [Reference Sloane14, A081577, A081578]. By Theorem 2.1, we can get the log-concavity of sequences in these two triangles.
Corollary 2.3 All the sequences located in a transversal of $D(2)$![]() (or $D(3)$
(or $D(3)$![]() ) or in a line parallel to the boundary of $D(2)$
) or in a line parallel to the boundary of $D(2)$![]() (or $D(3)$
(or $D(3)$![]() ) are log-concave.
) are log-concave.
Remark 2.4 A polynomial sequence $(a_i(q))_{i\geq 0}$![]() is called a $q$
is called a $q$![]() -Pólya frequency ($q$
-Pólya frequency ($q$![]() -PF for short) sequence if all minors of the corresponding Toeplitz matrix $[a_{i-j}(q)]_{i,j\geq 0}$
-PF for short) sequence if all minors of the corresponding Toeplitz matrix $[a_{i-j}(q)]_{i,j\geq 0}$![]() are $q$
are $q$![]() -non-negative. In fact, the polynomial sequence $(S_i(q))_{i\geq 0}$
-non-negative. In fact, the polynomial sequence $(S_i(q))_{i\geq 0}$![]() forms a q-PF sequence, which could be proved by the same technique used in the proof of Theorem $2$
forms a q-PF sequence, which could be proved by the same technique used in the proof of Theorem $2$![]() in [Reference Yu24].
in [Reference Yu24].
3. $q$ -total positivity of $D(q)$
-total positivity of $D(q)$
Let $f(q)$![]() and $g(q)$
and $g(q)$![]() be two real polynomials in $q$
be two real polynomials in $q$![]() . Let $M(q)=[m_{n,k}]_{n,k\geq 0}$
. Let $M(q)=[m_{n,k}]_{n,k\geq 0}$![]() be the matrix whose entries are all real polynomials in $q$
be the matrix whose entries are all real polynomials in $q$![]() . We say that $M(q)$
. We say that $M(q)$![]() is $q$
is $q$![]() -totally positive ( $q$
-totally positive ( $q$![]() -TP for short) if all minors are $q$
-TP for short) if all minors are $q$![]() -non-negative.
-non-negative.
Note that, since (1.4), the square matrix $[D_{n,k}(q)]_{n,k\geq 0}=PDP^{T}$![]() , where $P$
, where $P$![]() is the Pascal triangle and $D={\rm diag}(1,\,1+q,\,(1+q)^{2},\,(1+q)^{3},\,\ldots )$
is the Pascal triangle and $D={\rm diag}(1,\,1+q,\,(1+q)^{2},\,(1+q)^{3},\,\ldots )$![]() . Hence the $q$
. Hence the $q$![]() -total positivity of $[D_{n,k}(q)]_{n,k\geq 0}$
-total positivity of $[D_{n,k}(q)]_{n,k\geq 0}$![]() follows immediately from the Cauchy–Binet formula and the total positivity of the Pascal triangle (i.e., all its minors are non-negative).
follows immediately from the Cauchy–Binet formula and the total positivity of the Pascal triangle (i.e., all its minors are non-negative).
It is known that the triangle $D(q)$![]() is a Riordan array $(\frac {1}{1-x},\,\frac {x+qx^{2}}{1-x})$
is a Riordan array $(\frac {1}{1-x},\,\frac {x+qx^{2}}{1-x})$![]() (see [Reference Mu and Zheng12] for details). A (proper) Riordan array, denoted by $(d(x),\, h(x))$
(see [Reference Mu and Zheng12] for details). A (proper) Riordan array, denoted by $(d(x),\, h(x))$![]() , is an infinite lower triangular matrix whose generating function of the $k$
, is an infinite lower triangular matrix whose generating function of the $k$![]() th column is $d(x)h^{k}(x)$
th column is $d(x)h^{k}(x)$![]() for $k=0,\,1,\,2,\,\ldots$
for $k=0,\,1,\,2,\,\ldots$![]() , where $d(0)=1$
, where $d(0)=1$![]() , $h(0)=0$
, $h(0)=0$![]() and $h'(0)\neq 0$
and $h'(0)\neq 0$![]() . In this section, we consider the $q$
. In this section, we consider the $q$![]() -total positivity of $D(q)$
-total positivity of $D(q)$![]() . We first prove a lemma which is a $q$
. We first prove a lemma which is a $q$![]() -analogy of Theorem 3 in [Reference Mao, Mu and Wang11].
-analogy of Theorem 3 in [Reference Mao, Mu and Wang11].
Lemma 3.1 Let $M(q)=(d(x),\,h(x))$![]() be a Riordan array, where $d(x)=\sum \nolimits _{n\ge 0}d_n(q)x^{n}$
be a Riordan array, where $d(x)=\sum \nolimits _{n\ge 0}d_n(q)x^{n}$![]() and $h(x)=\sum \nolimits _{n\ge 0}h_n(q)x^{n}$
and $h(x)=\sum \nolimits _{n\ge 0}h_n(q)x^{n}$![]() . If the matrix
. If the matrix

is $q$![]() -TP, then so is the Riordan array $M(q)$
-TP, then so is the Riordan array $M(q)$![]() .
.
Proof. Let $T(q)=(h(x),\,x)=[h_{i-j}(q)]_{i,j\ge 0}$![]() and $v(q)=(d_0(q),\,d_1(q),\,\ldots )^{T}$
and $v(q)=(d_0(q),\,d_1(q),\,\ldots )^{T}$![]() . Then
. Then
Let $M_k(q)$![]() denote the submatrix $(v(q),\,T(q)v(q),\,\ldots,\,T(q)^{k-1}v(q))$
denote the submatrix $(v(q),\,T(q)v(q),\,\ldots,\,T(q)^{k-1}v(q))$![]() consisting of the first $k$
consisting of the first $k$![]() columns of $M(q)$
columns of $M(q)$![]() . Then
. Then

If $M_k(q)$![]() is $q$
is $q$![]() -TP, then so is $\left [\begin {smallmatrix} 1 & 0 \\ 0 & M_k(q) \\ \end {smallmatrix}\right ]$
-TP, then so is $\left [\begin {smallmatrix} 1 & 0 \\ 0 & M_k(q) \\ \end {smallmatrix}\right ]$![]() . The condition states that $(v(q),\,T(q))$
. The condition states that $(v(q),\,T(q))$![]() is $q$
is $q$![]() -TP. It follows that the product $M_{k+1}(q)$
-TP. It follows that the product $M_{k+1}(q)$![]() is also $q$
is also $q$![]() -TP from the classic Cauchy–Binet formula. Thus, the statement follows.
-TP from the classic Cauchy–Binet formula. Thus, the statement follows.
Theorem 3.2 The triangle $D(q)$![]() is $q$
is $q$![]() -totally positive.
-totally positive.
Proof. Note that $D(q)=(d(x),\,h(x))=(\frac {1}{1-x},\,\frac {x+qx^{2}}{1-x})$![]() . Let $T(q)=(h(x),\,x)$
. Let $T(q)=(h(x),\,x)$![]() and $v(q)=(d_0(q),\,d_1(q),\,d_2(q),\,\ldots )^{T}$
and $v(q)=(d_0(q),\,d_1(q),\,d_2(q),\,\ldots )^{T}$![]() . By Lemma 3.1, it suffices to show that $(v(q),\,T(q))$
. By Lemma 3.1, it suffices to show that $(v(q),\,T(q))$![]() is $q$
is $q$![]() -TP. We have
-TP. We have

One can check that both matrices on the right-hand side are $q$![]() -TP. Therefore, $(v(q),\,T(q))$
-TP. Therefore, $(v(q),\,T(q))$![]() is $q$
is $q$![]() -TP by the classic Cauchy–Binet formula, as required.
-TP by the classic Cauchy–Binet formula, as required.
4. Zeros of row sums
Let $R_n(q)=\sum \nolimits _i r_{n,i}q^{i}$![]() be the sum of the $n$
be the sum of the $n$![]() th row of $D(q)$
th row of $D(q)$![]() , i.e.,
, i.e.,

The first few entries of $(R_n(q))_{n\geq 0}$![]() are $(1,\,2,\,4+q,\,8+4q,\,\ldots )$
are $(1,\,2,\,4+q,\,8+4q,\,\ldots )$![]() . The coefficient matrix of $R_n(q)$
. The coefficient matrix of $R_n(q)$![]() is defined by the matrix
is defined by the matrix

Note that the polynomial $D_{n,k}(q)$![]() satisfies the recurrence (1.3), hence
satisfies the recurrence (1.3), hence
Thus, the row sum $R_n(q)$![]() satisfies the simple recurrence
satisfies the simple recurrence
with $R_1(q)=1$![]() , $R_2(q)=2$
, $R_2(q)=2$![]() .
.
Let $(f_n(z))_{n\ge 0}$![]() be a sequence of complex polynomials. We say that the complex number $z$
be a sequence of complex polynomials. We say that the complex number $z$![]() is a limit of zeros of the sequence $(f_n(z))_{n\ge 0}$
is a limit of zeros of the sequence $(f_n(z))_{n\ge 0}$![]() if there is such a sequence $(z_n)_{n\ge 0}$
if there is such a sequence $(z_n)_{n\ge 0}$![]() that $f_n(z_n)=0$
that $f_n(z_n)=0$![]() and $z_n\rightarrow z$
and $z_n\rightarrow z$![]() as $n\rightarrow +\infty$
as $n\rightarrow +\infty$![]() . Suppose now that $(f_n(z))_{n\ge 0}$
. Suppose now that $(f_n(z))_{n\ge 0}$![]() is a sequence of polynomials satisfying the recursion
is a sequence of polynomials satisfying the recursion

where $c_j(z)$![]() are polynomials in $z$
are polynomials in $z$![]() . Let $\lambda _j(z)$
. Let $\lambda _j(z)$![]() be all roots of the associated characteristic equation $\lambda ^{k}+\sum \nolimits _{j=1}^{k}c_j(z)\lambda ^{k-j}=0$
be all roots of the associated characteristic equation $\lambda ^{k}+\sum \nolimits _{j=1}^{k}c_j(z)\lambda ^{k-j}=0$![]() . It is well known that if $\lambda _j(z)$
. It is well known that if $\lambda _j(z)$![]() are distinct, then
are distinct, then

where $\alpha _j(z)$![]() is determined from the initial conditions.
is determined from the initial conditions.
Lemma 4.1 Beraha et al. [Reference Beraha, Kahane and Weiss4, Theorem]
Under the non-degeneracy requirements that in (4.2) no $\alpha _j(z)$![]() is identically zero and that no pair $i\neq j$
is identically zero and that no pair $i\neq j$![]() is $\lambda _i(z)\equiv \omega \lambda _j(z)$
is $\lambda _i(z)\equiv \omega \lambda _j(z)$![]() for some $\omega \in \mathbb {C}$
for some $\omega \in \mathbb {C}$![]() of unit modulus, then $z$
of unit modulus, then $z$![]() is a limit of zeros of $(f_n(z))_{n\ge 0}$
is a limit of zeros of $(f_n(z))_{n\ge 0}$![]() if and only if either
if and only if either
(i) two or more of the $\lambda _i(z)$
 are of equal modulus, and strictly greater (in modulus) than the others; or
are of equal modulus, and strictly greater (in modulus) than the others; or(ii) for some $j,$
 $\lambda _j(z)$
$\lambda _j(z)$ has modulus strictly greater than all the other $\lambda _i(z)$
has modulus strictly greater than all the other $\lambda _i(z)$ have, and $\alpha _j(z)=0$
have, and $\alpha _j(z)=0$ .
.
Theorem 4.2 Zeros of row sum $R_n(q)$![]() are real, distinct in $(-\infty,\, -1)$
are real, distinct in $(-\infty,\, -1)$![]() and are dense in the corresponding semi-closed interval $(-\infty,\, -1]$
and are dense in the corresponding semi-closed interval $(-\infty,\, -1]$![]() .
.
Proof. We first need to prove that

for which we only demonstrate the case that $n$![]() is even in the following since it is quite similar for odd $n$
is even in the following since it is quite similar for odd $n$![]() .
.
Note that
with $R_1=1$![]() , $R_2=2$
, $R_2=2$![]() . Hence the Binet form of the row sums is
. Hence the Binet form of the row sums is
where
are the roots of the characteristic equation $\lambda ^{2}-2\lambda -q=0$![]() . Let $\omega _k=e^{\frac {2k\pi i}{n+1}}$
. Let $\omega _k=e^{\frac {2k\pi i}{n+1}}$![]() . Then $\lambda ^{n+1}-1=\prod _{k=1}^{n+1}(\lambda -\omega _k)$
. Then $\lambda ^{n+1}-1=\prod _{k=1}^{n+1}(\lambda -\omega _k)$![]() . Note that
. Note that
Since $n$![]() is even, we have
is even, we have

and hence

Since $\lambda _1+\lambda _2=2$![]() and $\lambda _1\lambda _2=-q$
and $\lambda _1\lambda _2=-q$![]() , we have
, we have

Denote $z_{n,k}=-1/\cos ^{2}\frac {k\pi }{n+1},\,\ k=1,\,2,\,\cdots,\,n/2.$![]() Then the polynomial $R_n(q)$
Then the polynomial $R_n(q)$![]() has distinct real zeros $z_{n,1}>z_{n,2}>\cdots >z_{n,n/2}$
has distinct real zeros $z_{n,1}>z_{n,2}>\cdots >z_{n,n/2}$![]() . Since
. Since
all zeros of $R_n(q)$![]() are in $(-\infty,\, -1)$
are in $(-\infty,\, -1)$![]() .
.
We proceed to prove that each $q\in (-\infty,\, -1]$![]() is a limit of zeros of the sequence $(R_n(q))_{n\ge 0}$
is a limit of zeros of the sequence $(R_n(q))_{n\ge 0}$![]() . The non-degeneracy conditions of Lemma 4.1 are clearly satisfied by (4.4). So the limits of zeros of $(R_n(q))_{n\ge 0}$
. The non-degeneracy conditions of Lemma 4.1 are clearly satisfied by (4.4). So the limits of zeros of $(R_n(q))_{n\ge 0}$![]() are those $q$
are those $q$![]() for which $|\lambda _1(q)|=|\lambda _2(q)|$
for which $|\lambda _1(q)|=|\lambda _2(q)|$![]() , i.e.,
, i.e.,
by (4.5). In other words, $\sqrt {q+1}$![]() must be a pure imaginary. It follows that $q+1\le 0$
must be a pure imaginary. It follows that $q+1\le 0$![]() , i.e., $q\le -1$
, i.e., $q\le -1$![]() . Then the proof is completed.
. Then the proof is completed.
Let $A_n(q)$![]() be the sum of the $n$
be the sum of the $n$![]() th antidiagonal row of $D(q)$
th antidiagonal row of $D(q)$![]() , i.e.,
, i.e.,

The first few entries of $(A_n(q))_n$![]() are $(1,\,1,\,2,\,3+q,\,5+2q,\,\ldots )$
are $(1,\,1,\,2,\,3+q,\,5+2q,\,\ldots )$![]() . By (4.1), it is easy to check that $A_n(q)$
. By (4.1), it is easy to check that $A_n(q)$![]() satisfies
satisfies
with $A_1=1$![]() , $A_2=1$
, $A_2=1$![]() and $A_3=2$
and $A_3=2$![]() .
.
Theorem 4.3 Zeros of antidiagonal row sum $A_n(q)$![]() are in $(-\infty,\, -1]$
are in $(-\infty,\, -1]$![]() and are dense there.
and are dense there.
To prove this, we need the following lemma which can be found in [Reference Tran and Zumba20, Theorem 3].
Lemma 4.4 Consider the sequence of polynomials $\{P_n(q)\}_{n=0}^{\infty }$![]() generated by
generated by

where $a\in \mathbb {R}$![]() . If $-1\leq a\leq 1/3$
. If $-1\leq a\leq 1/3$![]() , then all the zeros of $P_n(q)$
, then all the zeros of $P_n(q)$![]() are in the real interval
are in the real interval

and are also dense in $I_a$![]() .
.
Proof of Theorem 4.3 By (4.6), the generating function of $A_n(q)$![]() follows that
follows that

which can also be derived from (4.7) with substitutions $x\rightarrow -x$![]() and $a\rightarrow -1$
and $a\rightarrow -1$![]() . So $A_n(q)$
. So $A_n(q)$![]() meets the condition of Lemma 4.4, and therefore, the zeros of $A_n(q)$
meets the condition of Lemma 4.4, and therefore, the zeros of $A_n(q)$![]() are in $(-\infty,\, -1]$
are in $(-\infty,\, -1]$![]() and are dense there.
and are dense there.
5. Remarks
In this section, we give some remarks on the asymptotic normality of coefficients of row sums. Let $a_{n,k}$![]() be a double-indexed sequence of non-negative numbers and let
be a double-indexed sequence of non-negative numbers and let

denote the normalized probabilities. Following Bender [Reference Bender3], we say that the sequence $a_{n,k}$![]() is asymptotically normal by a central limit theorem if
is asymptotically normal by a central limit theorem if

where $\mu _n$![]() and $\sigma ^{2}_n$
and $\sigma ^{2}_n$![]() are the mean and variance of $a_{n,k}$
are the mean and variance of $a_{n,k}$![]() , respectively. We say that $a_{n,k}$
, respectively. We say that $a_{n,k}$![]() is asymptotically normal by a local limit theorem on $\mathbb {R}$
is asymptotically normal by a local limit theorem on $\mathbb {R}$![]() if
if
In this case,

where $k=\mu _n+x\sigma _n$![]() and $x=O(1)$
and $x=O(1)$![]() . Clearly, the validity of (5.2) implies that of (5.1).
. Clearly, the validity of (5.2) implies that of (5.1).
Many well-known combinatorial sequences enjoy central and local limit theorems, such as the binomial coefficients $\binom {n}{k}$![]() , the signless Stirling numbers $c(n,\,k)$
, the signless Stirling numbers $c(n,\,k)$![]() of the first kind, the Stirling numbers $S(n,\,k)$
of the first kind, the Stirling numbers $S(n,\,k)$![]() of the second kind, the Eulerian numbers $A(n,\,k)$
of the second kind, the Eulerian numbers $A(n,\,k)$![]() [Reference Canfield6], and the Delannoy numbers $d(n,\,k)$
[Reference Canfield6], and the Delannoy numbers $d(n,\,k)$![]() [Reference Wang, Zheng and Chen21]. Besides, the asymptotic normality of Laplacian coefficients of graphs was discovered in [Reference Wang, Zhang and Zhu22]. A standard approach to demonstrating asymptotic normality is the following criterion (see [Reference Bender3, Theorem 2] for instance and [Reference Canfield6, Example 3.4.2] for historical remarks).
[Reference Wang, Zheng and Chen21]. Besides, the asymptotic normality of Laplacian coefficients of graphs was discovered in [Reference Wang, Zhang and Zhu22]. A standard approach to demonstrating asymptotic normality is the following criterion (see [Reference Bender3, Theorem 2] for instance and [Reference Canfield6, Example 3.4.2] for historical remarks).
Lemma 5.1 Suppose that $S_n(q)=\sum \nolimits _{k=0}^{n}a_{n,k}q^{k}$![]() have only real zeros and $S_n(q)=\prod _{i=1}^{n}(q+r_i),$
have only real zeros and $S_n(q)=\prod _{i=1}^{n}(q+r_i),$![]() where all $a_{n,k}$
where all $a_{n,k}$![]() and $r_i$
and $r_i$![]() are non-negative. Let
are non-negative. Let

and

Then if $\sigma _n^{2}\rightarrow +\infty,$![]() the numbers $a_{n,k}$
the numbers $a_{n,k}$![]() are asymptotically normal (by central and local limit theorems) with the mean $\mu _n$
are asymptotically normal (by central and local limit theorems) with the mean $\mu _n$![]() and variance $\sigma _n^{2}$
and variance $\sigma _n^{2}$![]() .
.
For the asymptotic normality of $r_{n,i}$![]() (the coefficients of row sums $R_n(q)$
(the coefficients of row sums $R_n(q)$![]() ), we have the following result.
), we have the following result.
Theorem 5.2 The coefficients $r_{n,i}$![]() are asymptotically normal (by central and local limit theorems) with the mean $\mu _n\sim \frac {(2-\sqrt 2)n}{4}$
are asymptotically normal (by central and local limit theorems) with the mean $\mu _n\sim \frac {(2-\sqrt 2)n}{4}$![]() and variance $\sigma _n^{2}\sim \frac {n}{8\sqrt 2}$
and variance $\sigma _n^{2}\sim \frac {n}{8\sqrt 2}$![]() .
.
Its proof can be similarly produced by referring to [Reference Wang, Zheng and Chen21, Theorem 3.2].
Acknowledgement
This work was supported in part by the National Natural Science Foundation of China (Nos. 11701249, 12101110), the Scientific Research Fund of Liaoning Provincial Education Department (Nos. LJKR0463, 2019-BS-152), and the Priority Academic Program Development of Jiangsu Higher Education Institutions. The authors wish to thank the referee for his/her valuable suggestions.
Declaration of Competing Interest
The authors declare that they have no conflict of interest.