We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate a dichotomy property for Hardy–Littlewood maximal operators, noncentred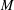 
$M$ and centred 
$M^{c}$, that was noticed by Bennett et al. [‘Weak-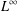
$L^{\infty }$ and BMO’, Ann. of Math. (2) 113 (1981), 601–611]. We illustrate the full spectrum of possible cases related to the occurrence or not of this property for 
$M$ and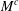 
$M^{c}$ in the context of nondoubling metric measure spaces 
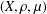$(X,\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707})$. In addition, if 
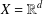$X=\mathbb{R}^{d}$, 
$d\geq 1$, and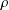 
$\unicode[STIX]{x1D70C}$ is the metric induced by an arbitrary norm on 
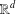$\mathbb{R}^{d}$, then we give the exact characterisation (in terms of 
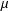$\unicode[STIX]{x1D707}$) of situations in which 
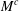$M^{c}$ possesses the dichotomy property provided that 
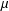$\unicode[STIX]{x1D707}$ satisfies some very mild assumptions.
$L^{p(\cdot )}$ OVER NONDOUBLING MEASURE SPACES
