For any prime p, let $y(p)$ denote the smallest integer y such that every reduced residue class (mod p) is represented by the product of some subset of $\{1,\dots ,y\}$ . It is easy to see that $y(p)$ is at least as large as the smallest quadratic nonresidue (mod p); we prove that $y(p) \ll _\varepsilon p^{1/(4 \sqrt e)+\varepsilon }$ , thus strengthening Burgess’ classical result. This result is of intermediate strength between two other results, namely Burthe’s proof that the multiplicative group (mod p) is generated by the integers up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ , and Munsch and Shparlinski’s result that every reduced residue class (mod p) is represented by the product of some subset of the primes up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ . Unlike the latter result, our proof is elementary and similar in structure to Burgess’ proof for the least quadratic nonresidue.

For each positive integer n, let $U(\mathbf {Z}/n\mathbf {Z})$ denote the group of units modulo n, which has order $\phi (n)$ (Euler’s function) and exponent $\lambda (n)$ (Carmichael’s function). The ratio $\phi (n)/\lambda (n)$ is always an integer, and a prime p divides this ratio precisely when the (unique) Sylow p-subgroup of $U(\mathbf {Z}/n\mathbf {Z})$ is noncyclic. Write W(n) for the number of such primes p. Banks, Luca, and Shparlinski showed that for certain constants $C_1, C_2>0$,

$$ \begin{align*} C_1 \frac{\log\log{n}}{(\log\log\log{n})^2} \le W(n) \le C_2 \log\log{n} \end{align*} $$

$\log \log {n}/\log \log \log {n}$

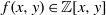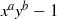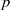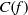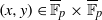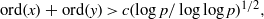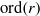Given $f(x,y)\in \mathbb Z[x,y]$ with no common components with $x^a-y^b$ and $x^ay^b-1$, we prove that for $p$ sufficiently large, with $C(f)$ exceptions, the solutions $(x,y)\in \overline {\mathbb F}_p\times \overline {\mathbb F}_p$ of $f(x,y)=0$ satisfy $ {\rm ord}(x)+{\rm ord}(y)\gt c (\log p/\log \log p)^{1/2},$ where $c$ is a constant and ${\rm ord}(r)$ is the order of $r$ in the multiplicative group 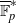$\overline {\mathbb F}_p^*$. Moreover, for most 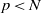$p\lt N$, 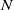$N$ being a large number, we prove that, with 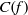$C(f)$ exceptions, ${\rm ord}(x)+{\rm ord}(y)\gt p^{1/4+\epsilon (p)},$ where $\epsilon (p)$ is an arbitrary function tending to 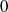$0$ when $p$ goes to 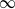$\infty $.

We discuss the problem of constructing elements of multiplicative high order in finite fields of large degree over their prime field. We obtain such elements by evaluating rational functions on elliptic curves, at points whose order is small with respect to their degree. We discuss several special cases, including an old construction of Wiedemann, giving the first nontrivial estimate for the order of the elements in this construction.

Nous démontrons une nouvelle minoration de la hauteur normalisée d’une sous-variété algébrique d’un tore multiplicatif (et par conséquent des petits points d’une telle sous-variété). Si dans le cas torique, une preuve effective de la conjecture de Bogomolov généralisée était déjà connue ainsi que des estimations “pluri-exponentielles” en le degré de la variété (Schmidt et Bombieri–Zannier), puis monomiales inverses (par le deuxième auteur et Philippon), notre approche qui est entièrement nouvelle, permet de démontrer à un $\varepsilon$-près les conjectures les plus précises (en fonction du degré) que l’on peut formuler dans ce cadre. On obtient ainsi pour ce problème l’exact analogue de ce que l’on sait obtenir dans le cadre du problème de Lehmer. Enfin, nous démontrons pour les sous-variétés de codimension au moins 2 une conjecture du deuxième auteur et Philippon.