Using the theory of 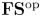 ${\mathbf {FS}} {^\mathrm {op}}$ modules, we study the asymptotic behavior of the homology of
${\mathbf {FS}} {^\mathrm {op}}$ modules, we study the asymptotic behavior of the homology of 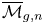 ${\overline {\mathcal {M}}_{g,n}}$, the Deligne–Mumford compactification of the moduli space of curves, for
${\overline {\mathcal {M}}_{g,n}}$, the Deligne–Mumford compactification of the moduli space of curves, for 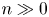 $n\gg 0$. An
$n\gg 0$. An 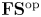 ${\mathbf {FS}} {^\mathrm {op}}$ module is a contravariant functor from the category of finite sets and surjections to vector spaces. Via copies that glue on marked projective lines, we give the homology of
${\mathbf {FS}} {^\mathrm {op}}$ module is a contravariant functor from the category of finite sets and surjections to vector spaces. Via copies that glue on marked projective lines, we give the homology of 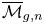 ${\overline {\mathcal {M}}_{g,n}}$ the structure of an
${\overline {\mathcal {M}}_{g,n}}$ the structure of an 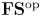 ${\mathbf {FS}} {^\mathrm {op}}$ module and bound its degree of generation. As a consequence, we prove that the generating function
${\mathbf {FS}} {^\mathrm {op}}$ module and bound its degree of generation. As a consequence, we prove that the generating function 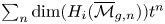 $\sum _{n} \dim (H_i({\overline {\mathcal {M}}_{g,n}})) t^n$ is rational, and its denominator has roots in the set
$\sum _{n} \dim (H_i({\overline {\mathcal {M}}_{g,n}})) t^n$ is rational, and its denominator has roots in the set 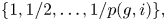 $\{1, 1/2, \ldots, 1/p(g,i)\},$ where
$\{1, 1/2, \ldots, 1/p(g,i)\},$ where  $p(g,i)$ is a polynomial of order
$p(g,i)$ is a polynomial of order  $O(g^2 i^2)$. We also obtain restrictions on the decomposition of the homology of
$O(g^2 i^2)$. We also obtain restrictions on the decomposition of the homology of  ${\overline {\mathcal {M}}_{g,n}}$ into irreducible
${\overline {\mathcal {M}}_{g,n}}$ into irreducible 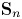 $\mathbf {S}_n$ representations.
$\mathbf {S}_n$ representations.
 $\mathcal {M}_{0}(\mathbb {P}^r, d)$, for
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, for  $d$ odd
$d$ odd
 $A_{\infty }$-STRUCTURES
$A_{\infty }$-STRUCTURES
 with Symmetric Divisors
with Symmetric Divisors