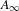Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-06T18:53:32.402Z Has data issue: false hasContentIssue false
  • English
  • Français

MODULI OF CURVES WITH NONSPECIAL DIVISORS AND RELATIVE MODULI OF $A_{\infty }$-STRUCTURES

Part of: Homological methods Curves

Published online by Cambridge University Press:  30 October 2017

Alexander Polishchuk
Alexander Polishchuk*
Affiliation:
University of Oregon, USA (apolish@uoregon.edu) National Research University Higher School of Economics, Russia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, for each 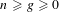$n\geqslant g\geqslant 0$ we consider the moduli stack 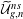$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ of curves $(C,p_{1},\ldots ,p_{n},v_{1},\ldots ,v_{n})$ of arithmetic genus $g$ with $n$ smooth marked points 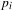$p_{i}$ and nonzero tangent vectors 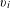$v_{i}$ at them, such that the divisor 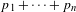$p_{1}+\cdots +p_{n}$ is nonspecial (has 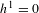$h^{1}=0$) and ample. With some mild restrictions on the characteristic we show that it is a scheme, affine over the Grassmannian 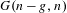$G(n-g,n)$. We also construct an isomorphism of 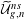$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ with a certain relative moduli of 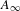$A_{\infty }$-structures (up to an equivalence) over a family of graded associative algebras parametrized by 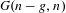$G(n-g,n)$.

Keywords

A∞-algebramoduli of curvesSato Grassmannian

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 16E45: Differential graded algebras and applications
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 6 , November 2019 , pp. 1295 - 1329
Copyright
© Cambridge University Press 2017 

Footnotes

Supported in part by the NSF grant DMS-1400390 and by the Russian Academic Excellence Project ‘5-100’.

References

Boggi, M., Compactifications of configurations of points on ¶1 and quadratic transformations of projective space, Indag. Math. (N.S.) 10 (1999), 191–202.Google Scholar
Ciocan-Fontanine, I. and Kapranov, M., Derived Hilbert schemes, J. Amer. Math. Soc. 15 (2002), 787–815.Google Scholar
Fedorchuk, M. and Smyth, D. I., Alternate compactifications of moduli spaces of curves, in Handbook of Moduli: Vol. I, pp. 331–414 (Int. Press, Somerville, MA, 2013).Google Scholar
Giansiracusa, N., Jensen, D. and Moon, H.-B., GIT compactifications of M 0, n and flips, Adv. Math. 248 (2013), 242–278.Google Scholar
Lekili, Y. and Perutz, T., Arithmetic mirror symmetry for the 2-torus, arxiv: 1211.4632.Google Scholar
Lekili, Y. and Polishchuk, A., A modular compactification of ${\mathcal{M}}_{1,n}$ from $A_{\infty }$ -structures, Crelle’s J., preprint arXiv:1408.0611 (to appear).Google Scholar
Manetti, M., Deformation theory via differential graded Lie algebras, Seminari di Geometria Algebrica 1998–1999 (Scuola Normale Superiore, 1999) arXiv:math.QA/0507284.Google Scholar
Mumford, D. and Fogarty, J., Geometric Invariant Theory (Springer-Verlag, Berlin, 1982).Google Scholar
Pinkham, H. C., Deformations of Algebraic Varieties with 𝔾m Action, Astérisque, 20, (Soc. Math. France, Paris, 1974).Google Scholar
Polishchuk, A., Moduli of curves as moduli of $A_{\infty }$ -structures, Duke Math. J., preprint arXiv:1312.4636 (to appear).Google Scholar
Polishchuk, A., Moduli of curves, Gröbner bases, and the Krichever map, Adv. Math. 305 (2017), 682–756.Google Scholar
Polishchuk, A., Moduli spaces of nonspecial pointed curves of arithmetic genus 1, Math. Ann. 369 (2017), 1021–1060.Google Scholar
Seidel, P., Homological mirror symmetry for the quartic surface, Mem. Amer. Math. Soc., Volume 236 (1116) (2015) vi+129pp.Google Scholar
Smyth, D. I., Modular compactifications of the space of pointed elliptic curves I, Compos. Math. 147(3) (2011), 877–913.Google Scholar
Smyth, D. I., Modular compactifications of the space of pointed elliptic curves II, Compos. Math. 147(6) (2011), 1843–1884.Google Scholar