Let 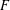 $F$ be an integral linear recurrence,
$F$ be an integral linear recurrence,  $G$ an integer-valued polynomial splitting over the rationals and
$G$ an integer-valued polynomial splitting over the rationals and 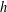 $h$ a positive integer. Also, let
$h$ a positive integer. Also, let 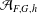 ${\mathcal{A}}_{F,G,h}$ be the set of all natural numbers
${\mathcal{A}}_{F,G,h}$ be the set of all natural numbers  $n$ such that
$n$ such that  $\gcd (F(n),G(n))=h$. We prove that
$\gcd (F(n),G(n))=h$. We prove that 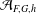 ${\mathcal{A}}_{F,G,h}$ has a natural density. Moreover, assuming that
${\mathcal{A}}_{F,G,h}$ has a natural density. Moreover, assuming that  $F$ is nondegenerate and
$F$ is nondegenerate and  $G$ has no fixed divisors, we show that the density of
$G$ has no fixed divisors, we show that the density of 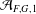 ${\mathcal{A}}_{F,G,1}$ is 0 if and only if
${\mathcal{A}}_{F,G,1}$ is 0 if and only if 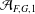 ${\mathcal{A}}_{F,G,1}$ is finite.
${\mathcal{A}}_{F,G,1}$ is finite.
 $n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE
$n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE  $n$TH TERM OF A LINEAR RECURRENCE
$n$TH TERM OF A LINEAR RECURRENCE