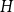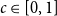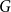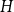Given a fixed graph $H$ and a constant $c \in [0,1]$, we can ask what graphs $G$ with edge density $c$ asymptotically maximise the homomorphism density of $H$ in 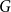$G$. For all 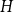$H$ for which this problem has been solved, the maximum is always asymptotically attained on one of two kinds of graphs: the quasi-star or the quasi-clique. We show that for any 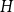$H$ the maximising 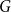$G$ is asymptotically a threshold graph, while the quasi-clique and the quasi-star are the simplest threshold graphs, having only two parts. This result gives us a unified framework to derive a number of results on graph homomorphism maximisation, some of which were also found quite recently and independently using several different approaches. We show that there exist graphs 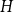$H$ and densities $c$ such that the optimising graph 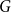$G$ is neither the quasi-star nor the quasi-clique (Day and Sarkar, SIAM J. Discrete Math. 35(1), 294–306, 2021). We also show that for $c$ large enough all graphs 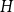$H$ maximise on the quasi-clique (Gerbner et al., J. Graph Theory 96(1), 34–43, 2021), and for any 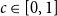$c \in [0,1]$ the density of $K_{1,2}$ is always maximised on either the quasi-star or the quasi-clique (Ahlswede and Katona, Acta Math. Hung. 32(1–2), 97–120, 1978). Finally, we extend our results to uniform hypergraphs.

We develop a theory of graph algebras over general fields. This is modelled after the theory developed by Freedman et al. (2007, J. Amer. Math. Soc.20 37–51) for connection matrices, in the study of graph homomorphism functions over real edge weight and positive vertex weight. We introduce connection tensors for graph properties. This notion naturally generalizes the concept of connection matrices. It is shown that counting perfect matchings, and a host of other graph properties naturally defined as Holant problems (edge models), cannot be expressed by graph homomorphism functions with both complex vertex and edge weights (or even from more general fields). Our necessary and sufficient condition in terms of connection tensors is a simple exponential rank bound. It shows that positive semidefiniteness is not needed in the more general setting.