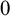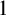1 results
ASYMPTOTIC TRUTH-VALUE LAWS IN MANY-VALUED LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
This paper studies which truth-values are most likely to be taken on finite models by arbitrary sentences of a many-valued predicate logic. The classical zero-one law (independently proved by Fagin and Glebskiĭ et al.) states that every sentence in a purely relational language is almost surely false or almost surely true, meaning that the probability that the formula is true in a randomly chosen finite structures of cardinal n is asymptotically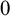
$0$ or 
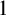$1$ as n grows to infinity. We obtain generalizations of this result for any logic with values in a finite lattice-ordered algebra, and for some infinitely valued logics, including Łukasiewicz logic. The finitely valued case is reduced to the classical one through a uniform translation and Oberschelp’s generalization of the zero-one law. Moreover, it is shown that the complexity of determining the almost sure value of a given sentence is PSPACE-complete (generalizing Grandjean’s result for the classical case), and for some logics we describe completely the set of truth-values that can be taken by sentences almost surely.
