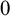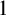1. Introduction
Given a property P of finite structures, a natural question has been often considered (beginning with [Reference Erdős16] in the context of graph theory): what is the probability that a structure satisfies P when randomly selected among finite structures with the same domain for a suitable probability measure? More interestingly, what are the asymptotic probabilities? Or, more precisely, what do these probabilities converge to (if anything) as the size of the domain of the structures grows to infinite? Sometimes, when the properties under consideration are expressible by formulas of a given logic, we may have a ‘zero-one law’: the probabilities converge to either
![]() $0$
or
$0$
or
![]() $1$
(and so we can say that the formula is either almost surely false or almost surely true). After early preliminary developments for monadic predicate logic [Reference Carnap11], the topic of logical zero-one laws was properly started independently in the papers by Glebskiĭ et al [Reference Glebskiĭ, Kogan, Liogon’kii and Talanov.19] and Fagin [Reference Fagin17] where they establish a zero-one law for first-order classical logic on finite purely relational vocabularies. The argument in [Reference Glebskiĭ, Kogan, Liogon’kii and Talanov.19] proceeds by a rather involved quantifier elimination, whereas the one in [Reference Fagin17] makes use of the so-called ‘extension axioms’ that form a complete theory axiomatizing a countable random structure. Lynch in [Reference Lynch33] attributes the discovery of this theory to Stanisław Jaśkowski; both the theory and the random structure appeared first in print in [Reference Gaifman18], where Gaifman acknowledged that the latter was an example suggested to him by Michael Rabin and Dana Scott. An important related result was obtained by Etienne Grandjean in [Reference Grandjean23] when he proved that the set of almost surely true formulas is PSPACE-complete. The reader may consult [Reference Ebbinghaus and Flum15, Reference Gurevich25, Reference Libkin32] for didactic introductions to zero-one laws and [Reference Compton and Rival14] for a rather comprehensive survey.
$1$
(and so we can say that the formula is either almost surely false or almost surely true). After early preliminary developments for monadic predicate logic [Reference Carnap11], the topic of logical zero-one laws was properly started independently in the papers by Glebskiĭ et al [Reference Glebskiĭ, Kogan, Liogon’kii and Talanov.19] and Fagin [Reference Fagin17] where they establish a zero-one law for first-order classical logic on finite purely relational vocabularies. The argument in [Reference Glebskiĭ, Kogan, Liogon’kii and Talanov.19] proceeds by a rather involved quantifier elimination, whereas the one in [Reference Fagin17] makes use of the so-called ‘extension axioms’ that form a complete theory axiomatizing a countable random structure. Lynch in [Reference Lynch33] attributes the discovery of this theory to Stanisław Jaśkowski; both the theory and the random structure appeared first in print in [Reference Gaifman18], where Gaifman acknowledged that the latter was an example suggested to him by Michael Rabin and Dana Scott. An important related result was obtained by Etienne Grandjean in [Reference Grandjean23] when he proved that the set of almost surely true formulas is PSPACE-complete. The reader may consult [Reference Ebbinghaus and Flum15, Reference Gurevich25, Reference Libkin32] for didactic introductions to zero-one laws and [Reference Compton and Rival14] for a rather comprehensive survey.
Zero-one laws have been only sporadically investigated in the the setting of many-valued logics, although they offer a number of intriguing issues that are invisible in the two-valued context. Indeed, in a many-valued setting we have a set of truth values A (with more than two elements) and formulas can take any element of A as a truth-value in a given structure. Given a formula
![]() $\varphi $
, we can say that
$\varphi $
, we can say that
![]() $\varphi $
takes a truth-value
$\varphi $
takes a truth-value
![]() $a \in A$
almost surely if the fraction of finite structures of cardinal n in which
$a \in A$
almost surely if the fraction of finite structures of cardinal n in which
![]() $\varphi $
takes value a tends to
$\varphi $
takes value a tends to
![]() $1$
as n grows to infinity. Then, a natural question is: do we have such general asymptotic truth-value laws for any many-valued logic? That is, in the presence of a multiplicity of truth-values, are some of the values taken by sentences almost surely? Exactly which of them? And, whenever we do have such a law, what is the complexity of determining the truth-value that an arbitrary formula almost surely takes?
$1$
as n grows to infinity. Then, a natural question is: do we have such general asymptotic truth-value laws for any many-valued logic? That is, in the presence of a multiplicity of truth-values, are some of the values taken by sentences almost surely? Exactly which of them? And, whenever we do have such a law, what is the complexity of determining the truth-value that an arbitrary formula almost surely takes?
Zero-one laws have indeed been obtained for some finitely valued fuzzy logics in [Reference Badia and Noguera5, Reference Kosik and Fermüller30], but, to the best of our knowledge, zero-one laws for infinitely valued logics remain largely unexplored. In the related context of semiring semantics, analogous issues have been recently put forward and successfully addressed by Grädel et al in [Reference Grädel, Helal, Naaf, Wilke, Baier and Fisman22] for sentences given in negation normal form (involving only the additional connectives of disjunction and conjunction) and letting interpretations assign truth-values directly to the literals (both atomic and negated atomic formulas) of the logic.
In this article, we consider asymptotic truth-value laws in many-valued logics with a general approach that allows for arbitrary probability measures and arbitrary lattice-based algebras, obtaining as main results:
-
• a general zero-one law for finitely valued predicate logics, and
-
• a zero-law for infinitely valued Łukasiewicz logic and other
 $[0,1]$
-valued predicate logics.
$[0,1]$
-valued predicate logics.
Moreover, for finitely values logics, we provide examples in which all values are almost sure and examples in which only a few are, and we generalize Grandjean’s theorem on the complexity of asymptotic truth-values.
The article is arranged as follows. In Section 2, we recall some necessary notions from classical finite model theory and its zero-one laws. In Section 3, we present our general approach to these issues in the case of finitely valued logics, in Section 3.1 we obtain the general zero-one law for finitely valued logics, in Section 3.2 we discuss random models (which are behind the proof of the previous result) and their axiomatizations, and in Section 3.3 we show that the complexity of the problem of determining the asymptotic truth-value of an arbitrary formula is in PSPACE and, actually, it is PSPACE-complete in the presence of crisp identity, hence generalizing Grandjean’s result for classical predicate logic. In Section 4, we provide natural examples of logics in which all truth-values are actually almost sure, and a rather wide class of logics in which the almost sure values are few. In Section 5, we prove the zero-one law for infinitely valued Łukasiewicz predicate logic. In Section 6, we consider again the problem of describing sets of almost sure values, now for infinitely valued logics, and we prove a zero-one law for a large family of
![]() $[0,1]$
-valued logics satisfying De Morgan laws. In particular, we obtain that all rational numbers in
$[0,1]$
-valued logics satisfying De Morgan laws. In particular, we obtain that all rational numbers in
![]() $[0,1]$
are almost sure values of infinitely valued Łukasiewicz predicate logic. Finally, Section 7 contains some concluding remarks and open questions.
$[0,1]$
are almost sure values of infinitely valued Łukasiewicz predicate logic. Finally, Section 7 contains some concluding remarks and open questions.
For readers less familiar with the literature on many-valued logic, a modern comprehensive reference in the general field of mathematical fuzzy logic is [Reference Cintula, Fermüller, Hájek and Noguera12], while [Reference Hájek26] remains even today a rather useful source that contains detailed proofs of many essential results; we recommend [Reference Mundici35] as a nice article highlighting the importance of infinitely valued Łukasiewicz logic among other non-classical logics.
2. Zero-one laws in two-valued predicate logic
In this section, we recall some facts from classical finite model theory that we aim to generalize later to the context of many-valued logics.
Consider first a purely relational vocabulary
![]() $\tau $
for the usual finitary first-order logic that we will denote by
$\tau $
for the usual finitary first-order logic that we will denote by
![]() $\mathcal {L}_{\omega \omega }$
, as it is customary in abstract model theory [Reference Barwise and Feferman6] and even in some works on many-valued logics (see, e.g., [Reference Badia and Noguera4]), where the
$\mathcal {L}_{\omega \omega }$
, as it is customary in abstract model theory [Reference Barwise and Feferman6] and even in some works on many-valued logics (see, e.g., [Reference Badia and Noguera4]), where the
![]() $\omega $
subscripts represent the finitary character of, respectively, conjunctions/disjunctions and quantifier strings. Sometimes, we will also refer to the stronger logics
$\omega $
subscripts represent the finitary character of, respectively, conjunctions/disjunctions and quantifier strings. Sometimes, we will also refer to the stronger logics
![]() $\mathcal {L}_{\omega _1\omega }$
and
$\mathcal {L}_{\omega _1\omega }$
and
![]() $\mathcal {L}_{\infty \omega }$
which allow for conjunctions and disjunctions of, respectively, countably many or arbitarily many formulas, while keeping the finitary character of quantifier strings.
$\mathcal {L}_{\infty \omega }$
which allow for conjunctions and disjunctions of, respectively, countably many or arbitarily many formulas, while keeping the finitary character of quantifier strings.
A
![]() $\tau $
-sentence is said to be parametric in the sense of [Reference Oberschelp and Jungnickel36, p. 277] (or, alternatively, it is an Oberschelp condition) if it is equivalent to a finite conjunction of first-order formulas of the form:
$\tau $
-sentence is said to be parametric in the sense of [Reference Oberschelp and Jungnickel36, p. 277] (or, alternatively, it is an Oberschelp condition) if it is equivalent to a finite conjunction of first-order formulas of the form:
which abbreviates
![]() $\forall x_{1}\dots \forall x_{k}\,(\bigwedge \nolimits _{i<j}\lnot (x_{i}=x_{j})\rightarrow \phi (x_{1},\dots ,x_{k}))$
, where
$\forall x_{1}\dots \forall x_{k}\,(\bigwedge \nolimits _{i<j}\lnot (x_{i}=x_{j})\rightarrow \phi (x_{1},\dots ,x_{k}))$
, where
![]() $\phi (x_{1},\dots ,x_{k})$
is a quantifier-free formula such that all of its atomic subformulas
$\phi (x_{1},\dots ,x_{k})$
is a quantifier-free formula such that all of its atomic subformulas
![]() $Rx_{i_{1}}\dots x_{i_{k}} $
distinct from identities have
$Rx_{i_{1}}\dots x_{i_{k}} $
distinct from identities have
In the case where
![]() $k=1$
, any formula
$k=1$
, any formula
![]() $\forall x\,\phi (x)$
where
$\forall x\,\phi (x)$
where
![]() $\phi $
is quantifier-free, is parametric. For example,
$\phi $
is quantifier-free, is parametric. For example,
![]() $\forall x\,\lnot Rxx\wedge \forall ^{\not =}x,y\,(Rxy\rightarrow Ryx)$
is parametric, whereas
$\forall x\,\lnot Rxx\wedge \forall ^{\not =}x,y\,(Rxy\rightarrow Ryx)$
is parametric, whereas
![]() $\forall ^{\not =}x,y,z\,(Rxy\wedge Ryz\rightarrow Rxz)$
is not. It is not difficult to check that any universal formula of the form
$\forall ^{\not =}x,y,z\,(Rxy\wedge Ryz\rightarrow Rxz)$
is not. It is not difficult to check that any universal formula of the form
![]() $\forall x_{1}\dots \forall x_{k}\,\phi (x_{1},\dots ,x_{k})$
where each atomic subformula of
$\forall x_{1}\dots \forall x_{k}\,\phi (x_{1},\dots ,x_{k})$
where each atomic subformula of
![]() $\phi $
distinct from identities contains all the variables
$\phi $
distinct from identities contains all the variables
![]() $x_{1},\dots ,x_{k}$
is parametric. A class of structures is called an Oberschelp class if it can be axiomatized by parametric sentences.
$x_{1},\dots ,x_{k}$
is parametric. A class of structures is called an Oberschelp class if it can be axiomatized by parametric sentences.
Oberschelp’s extension [Reference Oberschelp and Jungnickel36, Theorem 3] of the classical zero-one law says: on finite models and finite purely relational vocabularies, for any class
![]() $\mathbb {K}$
definable by a finite set of parametric sentences, any first-order sentence
$\mathbb {K}$
definable by a finite set of parametric sentences, any first-order sentence
![]() $\phi $
is almost surely satisfied by finite members of
$\phi $
is almost surely satisfied by finite members of
![]() $\mathbb {K}$
or almost surely not satisfied. More precisely, if
$\mathbb {K}$
or almost surely not satisfied. More precisely, if
![]() $\mathbb {K}_{n}$
is the set of models in
$\mathbb {K}_{n}$
is the set of models in
![]() $\mathbb {K}$
with domain
$\mathbb {K}$
with domain
![]() $[n]=\{1,\ldots ,n\},$
then
$[n]=\{1,\ldots ,n\},$
then
 $$ \begin{align*} \mu _{n}(\phi )=\frac{|\{\mathfrak{M}\in \mathbb{K}_{n}: \mathfrak{M\models } \phi \}|}{|\mathbb{K}_{n}|} \ \textit{converges to}\ 0 \ \textit{or}\ 1. \end{align*} $$
$$ \begin{align*} \mu _{n}(\phi )=\frac{|\{\mathfrak{M}\in \mathbb{K}_{n}: \mathfrak{M\models } \phi \}|}{|\mathbb{K}_{n}|} \ \textit{converges to}\ 0 \ \textit{or}\ 1. \end{align*} $$
Oberschelp’s result actually holds for sentences of the variable-bounded infinitary logic
![]() $\mathcal {L}_{\infty \omega }^{\omega }$
, i.e., the fragment of the infinitary logic
$\mathcal {L}_{\infty \omega }^{\omega }$
, i.e., the fragment of the infinitary logic
![]() $\mathcal {L}_{\infty \omega }$
determined by formulas containing finitely many variables only. This is a generalization of a well-known result by Kolaitis and Vardi for the class of all finite models [Reference Kolaitis and Vardi29]. An accessible presentation of these results can be found in [Reference Ebbinghaus and Flum15].
$\mathcal {L}_{\infty \omega }$
determined by formulas containing finitely many variables only. This is a generalization of a well-known result by Kolaitis and Vardi for the class of all finite models [Reference Kolaitis and Vardi29]. An accessible presentation of these results can be found in [Reference Ebbinghaus and Flum15].
If there are no Oberschelp conditions, the counting probability measure
![]() $\mu _{n}$
in the above zero-one law corresponds to assigning probability
$\mu _{n}$
in the above zero-one law corresponds to assigning probability
![]() $\frac {1}{2}$
to the probabilistically independent atomic events
$\frac {1}{2}$
to the probabilistically independent atomic events
![]() $R(i_{1},\ldots ,i_{k})$
,
$R(i_{1},\ldots ,i_{k})$
,
![]() $i_{1},\ldots ,i_{k}\in [n]$
, in the random model
$i_{1},\ldots ,i_{k}\in [n]$
, in the random model
![]() $\mathfrak {M}\in \mathbb {K}_{n}$
. The zero-one law holds, with the same asymptotic probability for each
$\mathfrak {M}\in \mathbb {K}_{n}$
. The zero-one law holds, with the same asymptotic probability for each
![]() $\phi $
, if the random model is obtained by assigning a fixed probability
$\phi $
, if the random model is obtained by assigning a fixed probability
![]() $p_{R}\in (0,1)$
to the atomic event
$p_{R}\in (0,1)$
to the atomic event
![]() $R(x_{i_1},\ldots ,x_{i_k})$
for each
$R(x_{i_1},\ldots ,x_{i_k})$
for each
![]() $R\in \tau $
.Footnote
1
There is a wealth of positive and negative results pertaining to the case in which
$R\in \tau $
.Footnote
1
There is a wealth of positive and negative results pertaining to the case in which
![]() $p_{R}$
varies with n (cf. [Reference Spencer37]) or the class
$p_{R}$
varies with n (cf. [Reference Spencer37]) or the class
![]() $\mathbb {K}$
is given by non-parametric conditions (cf. [Reference Grove, Halpern and Koller24]).
$\mathbb {K}$
is given by non-parametric conditions (cf. [Reference Grove, Halpern and Koller24]).
3. The case of finitely valued predicate logics
Let
![]() $\boldsymbol {A}={\langle {A,\wedge ^{\boldsymbol {A}},\vee ^{\boldsymbol {A}},\ldots } \rangle }$
be an algebra (which can be finite or infinite) with a lattice reduct
$\boldsymbol {A}={\langle {A,\wedge ^{\boldsymbol {A}},\vee ^{\boldsymbol {A}},\ldots } \rangle }$
be an algebra (which can be finite or infinite) with a lattice reduct
![]() ${\langle {A,\wedge ^{\boldsymbol {A}},\vee ^{\boldsymbol {A}}}\rangle }$
and possibly with additional operations. We will call
${\langle {A,\wedge ^{\boldsymbol {A}},\vee ^{\boldsymbol {A}}}\rangle }$
and possibly with additional operations. We will call
![]() $\boldsymbol {A}$
a lattice algebra. The underlying lattice may be bounded, in which case
$\boldsymbol {A}$
a lattice algebra. The underlying lattice may be bounded, in which case
![]() $0$
and
$0$
and
![]() $1$
will denote, respectively, the bottom and top element (which may, but need not, be denoted by constants of the signature of
$1$
will denote, respectively, the bottom and top element (which may, but need not, be denoted by constants of the signature of
![]() $\boldsymbol {A}$
).
$\boldsymbol {A}$
).
For the associated
![]() $\boldsymbol {A}$
-valued logic
$\boldsymbol {A}$
-valued logic
![]() $\mathcal {L}^{\boldsymbol {A}}$
and a first-order relational vocabulary
$\mathcal {L}^{\boldsymbol {A}}$
and a first-order relational vocabulary
![]() $\tau $
, the first-order logic
$\tau $
, the first-order logic
![]() $\mathcal {L}^{\boldsymbol {A}}(\tau )$
is built in the usual way from variables
$\mathcal {L}^{\boldsymbol {A}}(\tau )$
is built in the usual way from variables
![]() $x_{1},x_{2},\ldots $
, relation symbols in
$x_{1},x_{2},\ldots $
, relation symbols in
![]() $\tau $
, connectives
$\tau $
, connectives
![]() $\wedge , \vee , \ldots $
(corresponding to the operations of
$\wedge , \vee , \ldots $
(corresponding to the operations of
![]() $\boldsymbol {A}$
), and quantifiers
$\boldsymbol {A}$
), and quantifiers
![]() $\forall $
and
$\forall $
and
![]() $\exists $
.
$\exists $
.
Models are
![]() $\boldsymbol {A}$
-valued
$\boldsymbol {A}$
-valued
![]() $\tau $
-structures
$\tau $
-structures
![]() $\mathfrak {M}={\langle {M,R^{\mathfrak {M}}}\rangle }_{R\in \tau }$
with domain
$\mathfrak {M}={\langle {M,R^{\mathfrak {M}}}\rangle }_{R\in \tau }$
with domain
![]() $M\not =\emptyset $
, where
$M\not =\emptyset $
, where
![]() $R^{\mathfrak {M}}\colon M^{\tau (R)}\longrightarrow A$
, and
$R^{\mathfrak {M}}\colon M^{\tau (R)}\longrightarrow A$
, and
![]() $\tau (R)$
denotes the arity of
$\tau (R)$
denotes the arity of
![]() $R\in \tau $
;
$R\in \tau $
;
![]() $\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
will denote the class of all
$\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
will denote the class of all
![]() $\boldsymbol {A}$
-valued
$\boldsymbol {A}$
-valued
![]() $\tau $
-structures.
$\tau $
-structures.
Define inductively for each formula
![]() $\varphi (x_{1},\ldots ,x_{k})$
in
$\varphi (x_{1},\ldots ,x_{k})$
in
![]() $\mathcal {L}^{\boldsymbol {A}}(\tau )$
with k free variables, a mapping
$\mathcal {L}^{\boldsymbol {A}}(\tau )$
with k free variables, a mapping
![]() $||\varphi ||^{\mathfrak {M}}\colon M^{k}\longrightarrow A,$
interpreting the atomic formulas according to
$||\varphi ||^{\mathfrak {M}}\colon M^{k}\longrightarrow A,$
interpreting the atomic formulas according to
![]() $\mathfrak {M}$
, the connectives according to
$\mathfrak {M}$
, the connectives according to
![]() $\boldsymbol {A}$
, and the quantifiers as suprema and infima in
$\boldsymbol {A}$
, and the quantifiers as suprema and infima in
![]() $\boldsymbol {A}$
(
$\boldsymbol {A}$
(
![]() $\mathfrak {M}$
is supposed to be safe, that is, the required infima and suprema exist, which in the context of finite structures is always guaranteed).
$\mathfrak {M}$
is supposed to be safe, that is, the required infima and suprema exist, which in the context of finite structures is always guaranteed).
For a finite (or complete) algebra
![]() $\boldsymbol {A}$
, we may extend the semantics to the infinitary logic
$\boldsymbol {A}$
, we may extend the semantics to the infinitary logic
![]() $\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {A}}$
by setting
$\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {A}}$
by setting
![]() $||\bigwedge \nolimits _{n}\varphi _{n}||^{\mathfrak {M}}:=\inf _{n}||\varphi _{n}||^{\mathfrak {M}}$
(all formulas
$||\bigwedge \nolimits _{n}\varphi _{n}||^{\mathfrak {M}}:=\inf _{n}||\varphi _{n}||^{\mathfrak {M}}$
(all formulas
![]() $\varphi _{n}$
having free variables in a common finite set) and similarly for
$\varphi _{n}$
having free variables in a common finite set) and similarly for
![]() $\bigvee _{n}\varphi _{n}$
.
$\bigvee _{n}\varphi _{n}$
.
The classical logics
![]() $\mathcal {L}_{\omega \omega }$
and
$\mathcal {L}_{\omega \omega }$
and
![]() $\mathcal {L}_{\omega _{1}\omega }$
may be, respectively, identified with
$\mathcal {L}_{\omega _{1}\omega }$
may be, respectively, identified with
![]() $\mathcal {L}^{\boldsymbol {B}_{2}}$
and
$\mathcal {L}^{\boldsymbol {B}_{2}}$
and
![]() $\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {B}_{2}}$
, where
$\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {B}_{2}}$
, where
![]() $\boldsymbol {B}_{2}$
is the two-element Boolean algebra.
$\boldsymbol {B}_{2}$
is the two-element Boolean algebra.
3.1. The zero-one law for finitely valued predicate logics
Let
![]() $\boldsymbol {A}$
be a finite lattice algebra,
$\boldsymbol {A}$
be a finite lattice algebra,
![]() $\tau \,$
a finite relational vocabulary, and
$\tau \,$
a finite relational vocabulary, and
![]() $\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
be the class of
$\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
be the class of
![]() $\boldsymbol {A}$
-valued
$\boldsymbol {A}$
-valued
![]() $\tau $
-structures with domain
$\tau $
-structures with domain
![]() $[n]=\{1,\ldots ,n\}$
.Footnote
2
Given
$[n]=\{1,\ldots ,n\}$
.Footnote
2
Given
![]() $\varphi (x_{1},\ldots ,x_{k})\in \mathcal {L}^{\boldsymbol {A}}(\tau )$
,
$\varphi (x_{1},\ldots ,x_{k})\in \mathcal {L}^{\boldsymbol {A}}(\tau )$
,
![]() $i_{1},\ldots ,i_{k}\leq n,$
and
$i_{1},\ldots ,i_{k}\leq n,$
and
![]() $a\in A$
, define the probability that a randomly chosen model
$a\in A$
, define the probability that a randomly chosen model
![]() $\mathfrak {M} \in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
assigns the value a to
$\mathfrak {M} \in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
assigns the value a to
![]() $\varphi (i_{1},\ldots ,i_{k})$
as:
$\varphi (i_{1},\ldots ,i_{k})$
as:
 $$ \begin{align*} \mu _{n}(\varphi (i_{1},\ldots,i_{k})=a):=\frac{|\{\mathfrak{M}\in \mathrm{Mod}_{\tau,n}^{\boldsymbol{A}}: ||\varphi ||^{\mathfrak{M}}(i_{1},\ldots,i_{k})=a\}|}{|\mathrm{Mod}_{\tau ,n}^{\boldsymbol{A}}|}. \end{align*} $$
$$ \begin{align*} \mu _{n}(\varphi (i_{1},\ldots,i_{k})=a):=\frac{|\{\mathfrak{M}\in \mathrm{Mod}_{\tau,n}^{\boldsymbol{A}}: ||\varphi ||^{\mathfrak{M}}(i_{1},\ldots,i_{k})=a\}|}{|\mathrm{Mod}_{\tau ,n}^{\boldsymbol{A}}|}. \end{align*} $$
This definition assigns the same weight to all models in
![]() $\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}},$
and the same probability
$\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}},$
and the same probability
to the event that an atomic statement
![]() $R(i_{1},\ldots ,i_{\tau (R)})$
takes the value
$R(i_{1},\ldots ,i_{\tau (R)})$
takes the value
![]() $a\in A,$
for any a and numbers
$a\in A,$
for any a and numbers
![]() $i_{1},\ldots ,i_{\tau (R)}\in [n]$
.
$i_{1},\ldots ,i_{\tau (R)}\in [n]$
.
More generally, and reciprocally, we may fix, for each
![]() $R\in \tau $
a probability distribution
$R\in \tau $
a probability distribution
![]() $p_{R} \colon A\longrightarrow [0,1]$
(that is,
$p_{R} \colon A\longrightarrow [0,1]$
(that is,
![]() $\sum _{a\in A}p_{R}(a)=1$
) such that
$\sum _{a\in A}p_{R}(a)=1$
) such that
![]() $p_{R}(a)>0$
for any
$p_{R}(a)>0$
for any
![]() $a\in A$
, and define a probability distribution Pr
$a\in A$
, and define a probability distribution Pr
![]() $_{n}\colon \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}\longrightarrow [0,1]$
in the class of
$_{n}\colon \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}\longrightarrow [0,1]$
in the class of
![]() $\boldsymbol {A}$
-valued models with domain
$\boldsymbol {A}$
-valued models with domain
![]() $[n]$
:
$[n]$
:
obtained by identifying
![]() $\mathfrak {M}$
with its atomic
$\mathfrak {M}$
with its atomic
![]() $\boldsymbol {A}$
-valued diagram. Then, we may define for any formula
$\boldsymbol {A}$
-valued diagram. Then, we may define for any formula
![]() $\varphi (x_{1},\ldots ,x_{k})\in \mathcal {L}^{\boldsymbol {A}}(\tau )$
,
$\varphi (x_{1},\ldots ,x_{k})\in \mathcal {L}^{\boldsymbol {A}}(\tau )$
,
![]() $a\in A,$
and
$a\in A,$
and
![]() $i_{1},\ldots ,i_{k}\in [n],$
$i_{1},\ldots ,i_{k}\in [n],$
Notice that, for the sake of clarity, we are using the simplified notation
![]() $\varphi (i_{1},\ldots ,i_{k})=a$
to denote the event
$\varphi (i_{1},\ldots ,i_{k})=a$
to denote the event
![]() $ ||\varphi ||^{\mathfrak {M}}(i_{1},\ldots ,i_{k})=a$
for an arbitrary model
$ ||\varphi ||^{\mathfrak {M}}(i_{1},\ldots ,i_{k})=a$
for an arbitrary model
![]() $\mathfrak {M}\in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
.
$\mathfrak {M}\in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
.
It is not hard to check that, under this definition,
and the atomic events
![]() $R(i_{1},\ldots ,i_{k})=a$
,
$R(i_{1},\ldots ,i_{k})=a$
,
![]() $R^{\prime }(j_{1},\ldots ,j_{k})=b$
are (probabilistically) independent if
$R^{\prime }(j_{1},\ldots ,j_{k})=b$
are (probabilistically) independent if
![]() $R \neq R'$
or
$R \neq R'$
or
![]() ${\langle {i_{1},\ldots ,i_{k}}\rangle } \neq {\langle {j_{1},\ldots ,j_{k}}\rangle }$
.
${\langle {i_{1},\ldots ,i_{k}}\rangle } \neq {\langle {j_{1},\ldots ,j_{k}}\rangle }$
.
The next theorem generalizes the classical zero-one law to the finitely-valued context.
Theorem 1. For any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
and
$\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
and
![]() $a\in A$
,
$a\in A$
,
![]() $\lim _{n}\mu _{n}(\varphi =a)=1$
or
$\lim _{n}\mu _{n}(\varphi =a)=1$
or
![]() $\lim _{n}\mu _{n}(\varphi =a)=0$
. Equivalently, for any sentence
$\lim _{n}\mu _{n}(\varphi =a)=0$
. Equivalently, for any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, there is a (unique)
$\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, there is a (unique)
![]() $a\in A$
such that
$a\in A$
such that
![]() $\lim _{n}\mu _{n}(\varphi =a)=1$
.
$\lim _{n}\mu _{n}(\varphi =a)=1$
.
Proof. The equivalence of both statements follows from the fact that, for each
![]() $\varphi $
, the events
$\varphi $
, the events
![]() $\varphi =a$
, with
$\varphi =a$
, with
![]() $a\in A$
, are exhaustive and mutually incompatible. The first formulation follows from the classical zero-one laws via the following multi-translation
$a\in A$
, are exhaustive and mutually incompatible. The first formulation follows from the classical zero-one laws via the following multi-translation
![]() $\theta \longmapsto {\langle {\theta ^{a}}\rangle }_{a\in A}$
, defined by simultaneous induction, from
$\theta \longmapsto {\langle {\theta ^{a}}\rangle }_{a\in A}$
, defined by simultaneous induction, from
![]() $\mathcal {L}^{\boldsymbol {A}}(\tau )$
into classical
$\mathcal {L}^{\boldsymbol {A}}(\tau )$
into classical
![]() $\mathcal {L}_{\omega \omega }(\tau \times A)$
,
$\mathcal {L}_{\omega \omega }(\tau \times A)$
,
![]() $\tau \times A=\{R^{a}:R\in \tau ,a\in A\}$
:
$\tau \times A=\{R^{a}:R\in \tau ,a\in A\}$
:
![]() $\circ (\varphi _{1},\ldots ,\varphi _{k})^{a}:=\bigvee _{\circ ^{\boldsymbol {A}}(b_{1},\ldots ,b_{k})=a}\varphi _{1}^{b_{1}}\wedge \ldots \wedge \varphi _{k}^{b_{k}}$
, for any connective
$\circ (\varphi _{1},\ldots ,\varphi _{k})^{a}:=\bigvee _{\circ ^{\boldsymbol {A}}(b_{1},\ldots ,b_{k})=a}\varphi _{1}^{b_{1}}\wedge \ldots \wedge \varphi _{k}^{b_{k}}$
, for any connective
![]() $\circ $
of arity k in the signature of
$\circ $
of arity k in the signature of
![]() $\boldsymbol {A}$
$\boldsymbol {A}$
 $$ \begin{align*} &(\forall x\varphi )^{a}:=(\bigvee\nolimits_{b_{1}\wedge \ldots\wedge b_{m}=a,\text{ }m\leq |A|}\exists x\,\varphi^{b_{1}}\wedge \ldots\wedge \exists x\,\varphi^{b_{m}})\wedge \forall x\,(\bigvee\nolimits_{b\geq a}\varphi ^{b})\\ &(\exists x\,\varphi )^{a}:=(\bigvee\nolimits_{b_{1}\vee \ldots\vee b_{m}=a,\text{ }m\leq|A|}\exists x\,\varphi^{b_{1}}\wedge \ldots\wedge \exists x\, \varphi^{b_{m}})\wedge \forall x\,(\bigvee\nolimits_{b\leq a}\varphi ^{b}), \end{align*} $$
$$ \begin{align*} &(\forall x\varphi )^{a}:=(\bigvee\nolimits_{b_{1}\wedge \ldots\wedge b_{m}=a,\text{ }m\leq |A|}\exists x\,\varphi^{b_{1}}\wedge \ldots\wedge \exists x\,\varphi^{b_{m}})\wedge \forall x\,(\bigvee\nolimits_{b\geq a}\varphi ^{b})\\ &(\exists x\,\varphi )^{a}:=(\bigvee\nolimits_{b_{1}\vee \ldots\vee b_{m}=a,\text{ }m\leq|A|}\exists x\,\varphi^{b_{1}}\wedge \ldots\wedge \exists x\, \varphi^{b_{m}})\wedge \forall x\,(\bigvee\nolimits_{b\leq a}\varphi ^{b}), \end{align*} $$
and the corresponding model transformations from
![]() $\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
into
$\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
into
![]() $\mathrm {Mod}_{\tau \times A}$
:
$\mathrm {Mod}_{\tau \times A}$
:
where
![]() $(R^{a})^{\mathfrak {M}_{\tau \times A}}:=\{\overline {i}\in M : R^{\mathfrak {M}}(\overline {i})=a\}$
, which are easily seen to satisfy:
$(R^{a})^{\mathfrak {M}_{\tau \times A}}:=\{\overline {i}\in M : R^{\mathfrak {M}}(\overline {i})=a\}$
, which are easily seen to satisfy:
The model transformations establish a domain-preserving bijection between
![]() $\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
and the class
$\mathrm {Mod}_{\tau }^{\boldsymbol {A}}$
and the class
![]() $\mathbb {K}\subseteq \mathrm {Mod}_{\tau \times A}$
of classical models of the parametric
$\mathbb {K}\subseteq \mathrm {Mod}_{\tau \times A}$
of classical models of the parametric
![]() $(\tau \times A)$
-sentences
$(\tau \times A)$
-sentences
 $$ \begin{align*} &\forall x_{1}\ldots x_{\tau (R)}\,\bigvee\nolimits_{a\in A}R^{a}(x_{1},\ldots,x_{\tau (R)}),\\ &\forall x_{1}\ldots x_{\tau (R)}\,\bigwedge\nolimits_{a\not=b}\lnot (R^{a}(x_{1},\ldots,x_{\tau(R)})\wedge R^{b}(x_{1},\ldots,x_{\tau (R)})). \end{align*} $$
$$ \begin{align*} &\forall x_{1}\ldots x_{\tau (R)}\,\bigvee\nolimits_{a\in A}R^{a}(x_{1},\ldots,x_{\tau (R)}),\\ &\forall x_{1}\ldots x_{\tau (R)}\,\bigwedge\nolimits_{a\not=b}\lnot (R^{a}(x_{1},\ldots,x_{\tau(R)})\wedge R^{b}(x_{1},\ldots,x_{\tau (R)})). \end{align*} $$
Being an Oberschelp class,
![]() $\mathbb {K}$
satisfies the classical zero-one law if we assign probability
$\mathbb {K}$
satisfies the classical zero-one law if we assign probability
![]() $\mu _{n}^{\mathbb {K}}(R^{a}(x_{1},\ldots ,x_{k})):=p_{R}(a)$
to the classical atomic events
$\mu _{n}^{\mathbb {K}}(R^{a}(x_{1},\ldots ,x_{k})):=p_{R}(a)$
to the classical atomic events
![]() $R^{a}(x_{1},\ldots ,x_{k})$
. The latter assignment yields
$R^{a}(x_{1},\ldots ,x_{k})$
. The latter assignment yields
![]() $\Pr _{n}(\mathfrak {M}_{\tau \times A})=\Pr _{n}(\mathfrak {M)}$
for
$\Pr _{n}(\mathfrak {M}_{\tau \times A})=\Pr _{n}(\mathfrak {M)}$
for
![]() $\mathfrak {M} \in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
and the transformation is bijective from
$\mathfrak {M} \in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
and the transformation is bijective from
![]() $\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
onto
$\mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}}$
onto
![]() $\mathbb {K}_n$
(models in
$\mathbb {K}_n$
(models in
![]() $\mathbb {K}$
with domain
$\mathbb {K}$
with domain
![]() $[n]$
). Then,
$[n]$
). Then,
![]() $\mu _{n}(\varphi =a)=\\ \mu _{n}\{\mathfrak {M}\in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}} : ||\varphi ||^{\mathfrak {M}}=a\}=\mu _{n}^{\mathbb {K}}\{\mathfrak {M}_{\tau \times A}\in \mathbb {K}_{n} : \mathfrak {M}_{\tau \times A}\models \varphi ^{a}\}=\mu _{n}^{\mathbb {K}}(\varphi ^{a})$
. Thus,
$\mu _{n}(\varphi =a)=\\ \mu _{n}\{\mathfrak {M}\in \mathrm {Mod}_{\tau ,n}^{\boldsymbol {A}} : ||\varphi ||^{\mathfrak {M}}=a\}=\mu _{n}^{\mathbb {K}}\{\mathfrak {M}_{\tau \times A}\in \mathbb {K}_{n} : \mathfrak {M}_{\tau \times A}\models \varphi ^{a}\}=\mu _{n}^{\mathbb {K}}(\varphi ^{a})$
. Thus,
![]() $\mu _{n}(\varphi =a)$
converges to
$\mu _{n}(\varphi =a)$
converges to
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Remark 2. Theorem 1 holds if the models are restricted to any class of
![]() $\boldsymbol {A}$
-valued structures satisfying conditions that are parametrically expressible in
$\boldsymbol {A}$
-valued structures satisfying conditions that are parametrically expressible in
![]() $\mathcal {L}_{\omega \omega }(\tau \times A)$
via the translation. Just add these conditions to the definition of the class
$\mathcal {L}_{\omega \omega }(\tau \times A)$
via the translation. Just add these conditions to the definition of the class
![]() $\mathbb {K}$
in the proof. For example,
$\mathbb {K}$
in the proof. For example,
![]() $\boldsymbol {A}$
-valued irreflexive symmetric graphs:
$\boldsymbol {A}$
-valued irreflexive symmetric graphs:
 $$ \begin{align*} &\quad \forall x\, R^{0}xx, \forall ^{\not=}xy\,\bigwedge\nolimits_{a\in A}(R^{a}xy\leftrightarrow R^{a}yx)\ (\textit{irreflexivity is expressed by using}\\ &\quad\textit{degree 0 on the relation}), \end{align*} $$
$$ \begin{align*} &\quad \forall x\, R^{0}xx, \forall ^{\not=}xy\,\bigwedge\nolimits_{a\in A}(R^{a}xy\leftrightarrow R^{a}yx)\ (\textit{irreflexivity is expressed by using}\\ &\quad\textit{degree 0 on the relation}), \end{align*} $$
or structures with crisp identity:
Remark 3. Theorem 1 holds also for sentences in finite vocabularies of the variable-bounded sublogic
![]() $(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{\omega }$
of
$(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{\omega }$
of
![]() $\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {A}}$
, where each formula has finitely many free and bound variables, because of the obvious extension of the translation to the infinitary logic; for example,
$\mathcal {L}_{\omega _{1}\omega }^{\boldsymbol {A}}$
, where each formula has finitely many free and bound variables, because of the obvious extension of the translation to the infinitary logic; for example,
 $$ \begin{align*}(\bigwedge\nolimits_{n}\varphi _{n})^{a}:=\big[\bigvee_{b_{1}\wedge \ldots\wedge b_{k}=a,k\leq |A|,n_{1},\ldots,n_{k}}(\varphi_{n_{1}}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{b_{m}})\big]\wedge \bigwedge\nolimits_{n}\bigvee _{b\geq a}\varphi _{n}^{b}, \end{align*} $$
$$ \begin{align*}(\bigwedge\nolimits_{n}\varphi _{n})^{a}:=\big[\bigvee_{b_{1}\wedge \ldots\wedge b_{k}=a,k\leq |A|,n_{1},\ldots,n_{k}}(\varphi_{n_{1}}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{b_{m}})\big]\wedge \bigwedge\nolimits_{n}\bigvee _{b\geq a}\varphi _{n}^{b}, \end{align*} $$
sends it to classical
![]() $\mathcal {L}_{\omega _{1}\omega }^{\omega }$
, known to satisfy the zero-one law under Oberschelp’s conditions [Reference Ebbinghaus and Flum15, Reference Kolaitis and Vardi29]).
$\mathcal {L}_{\omega _{1}\omega }^{\omega }$
, known to satisfy the zero-one law under Oberschelp’s conditions [Reference Ebbinghaus and Flum15, Reference Kolaitis and Vardi29]).
Remark 4. Zero-one laws have been studied for classical modal logics (e.g., [Reference Goranko and Kapron21, Reference Halpern and Kapron27, Reference Le Bars31, Reference Verbrugge39]). In [Reference Halpern and Kapron27], the authors prove zero-one laws for model validity for various systems of modal logic and state a similar result for frame validity. Unfortunately, the latter is refuted in [Reference Le Bars31] using ideas from [Reference Goranko and Kapron21]. In the finitely valued case, any fully modal sentence of the
![]() $\boldsymbol {A}$
-valued version S
$\boldsymbol {A}$
-valued version S
![]() $5_{c}^{\boldsymbol {A}}$
of propositional bimodal logic S
$5_{c}^{\boldsymbol {A}}$
of propositional bimodal logic S
![]() $5$
over finite universal crisp frames (cf. [Reference Caicedo, Metcalfe, Rodríguez and Rogger9, Reference Caicedo and Rodríguez10]) satisfies a zero-one law for model validity, because this logic may be interpreted as the one-variable fragment of
$5$
over finite universal crisp frames (cf. [Reference Caicedo, Metcalfe, Rodríguez and Rogger9, Reference Caicedo and Rodríguez10]) satisfies a zero-one law for model validity, because this logic may be interpreted as the one-variable fragment of
![]() $\mathcal {L}^{\boldsymbol {A}}$
on unary predicates via the translation
$\mathcal {L}^{\boldsymbol {A}}$
on unary predicates via the translation
![]() $\varphi \mapsto \widehat {\varphi }$
:
$\varphi \mapsto \widehat {\varphi }$
:
 $$ \begin{align*} &\widehat{p_{i}}:=P_{i}(w)\\ &\widehat{\square \varphi}:=\forall w\widehat{\varphi }(w)\\ &\widehat{\vphantom{A^,}\Diamond \varphi}:=\exists w\widehat{\varphi }(w)\\ &\widehat{t(\varphi _{1},\ldots,\varphi _{k})}:=t(\widehat{\varphi }_{1}(w),\ldots,\widehat{\varphi }_{k}(w)), \end{align*} $$
$$ \begin{align*} &\widehat{p_{i}}:=P_{i}(w)\\ &\widehat{\square \varphi}:=\forall w\widehat{\varphi }(w)\\ &\widehat{\vphantom{A^,}\Diamond \varphi}:=\exists w\widehat{\varphi }(w)\\ &\widehat{t(\varphi _{1},\ldots,\varphi _{k})}:=t(\widehat{\varphi }_{1}(w),\ldots,\widehat{\varphi }_{k}(w)), \end{align*} $$
which sends any fully modal formula to a sentence.
3.2. Finitely valued random models and extension axioms
In the above proof, the finitely valued zero-one law lurks a countable
![]() $\boldsymbol {A}$
-valued random model, corresponding to the classical random model that one obtains for the language of the translation.
$\boldsymbol {A}$
-valued random model, corresponding to the classical random model that one obtains for the language of the translation.
Theorem 5. There is a countable
![]() $\boldsymbol {A}$
-valued
$\boldsymbol {A}$
-valued
![]() $\tau $
-model
$\tau $
-model
![]() $\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
such that, for any sentence
$\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
such that, for any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, we have
$\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, we have
![]() $\lim _n \mu _{n}(\varphi =a)= 1$
iff
$\lim _n \mu _{n}(\varphi =a)= 1$
iff
![]() $||\varphi ||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=a $
.
$||\varphi ||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=a $
.
Proof. Take the
![]() $\boldsymbol {A}$
-model
$\boldsymbol {A}$
-model
![]() $\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
corresponding to the countable
$\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
corresponding to the countable
![]() $\omega $
-categorical random model
$\omega $
-categorical random model
![]() $\mathfrak {R}_{\tau \times A}$
of the class
$\mathfrak {R}_{\tau \times A}$
of the class
![]() $\mathbb {K}$
introduced in the proof of Theorem 1. Then,
$\mathbb {K}$
introduced in the proof of Theorem 1. Then,
![]() $\lim _n\mu _{n}(\varphi =a)= 1$
iff
$\lim _n\mu _{n}(\varphi =a)= 1$
iff
![]() $\lim _n \mu _{n}^{\mathbb {K}}(\varphi ^{a})= 1$
iff
$\lim _n \mu _{n}^{\mathbb {K}}(\varphi ^{a})= 1$
iff
![]() $\mathfrak {R}_{\tau \times A}\models \varphi ^{a}$
iff
$\mathfrak {R}_{\tau \times A}\models \varphi ^{a}$
iff
![]() $||\varphi ||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=a$
.
$||\varphi ||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=a$
.
The classical extension axioms characterizing
![]() $\mathfrak {R}_{\tau \times A}$
, and indirectly
$\mathfrak {R}_{\tau \times A}$
, and indirectly
![]() $\mathfrak {R}^{\boldsymbol {A}}_{\tau }$
, are rarely expressible in
$\mathfrak {R}^{\boldsymbol {A}}_{\tau }$
, are rarely expressible in
![]() $\mathcal {L}^{\boldsymbol {A}}$
, but they are expressible in (
$\mathcal {L}^{\boldsymbol {A}}$
, but they are expressible in (
![]() $\mathcal {L}_{\omega \omega })_{\tau \times A}$
as:
$\mathcal {L}_{\omega \omega })_{\tau \times A}$
as:
where
![]() $F_{k+1}$
is the set of atomic
$F_{k+1}$
is the set of atomic
![]() $\tau $
-formulas with variables in
$\tau $
-formulas with variables in
![]() $x_{1},\ldots ,x_{k},x_{k+1}$
, truly containing the variable
$x_{1},\ldots ,x_{k},x_{k+1}$
, truly containing the variable
![]() $x_{k+1}$
, and
$x_{k+1}$
, and
![]() $f\colon F_{k+1}\longrightarrow A$
. These axioms are automatically consistent with the set of parametric sentences defining the class
$f\colon F_{k+1}\longrightarrow A$
. These axioms are automatically consistent with the set of parametric sentences defining the class
![]() $\mathbb {K}$
in the proof of Theorem 1. If there are additional parametric conditions, only the extension axioms consistent with them are considered.
$\mathbb {K}$
in the proof of Theorem 1. If there are additional parametric conditions, only the extension axioms consistent with them are considered.
Example 6. According to Remark 2, the random
![]() $\boldsymbol {A}$
-valued irreflexive symmetric graph may be described as the unique countable
$\boldsymbol {A}$
-valued irreflexive symmetric graph may be described as the unique countable
![]() $\boldsymbol {A}$
-weighted irreflexive symmetric graph
$\boldsymbol {A}$
-weighted irreflexive symmetric graph
![]() $\mathfrak {R}={\langle {G,R}\rangle }$
such that, for any distinct
$\mathfrak {R}={\langle {G,R}\rangle }$
such that, for any distinct
![]() $x_{1},\ldots ,x_{k}\in G$
and
$x_{1},\ldots ,x_{k}\in G$
and
![]() $a_1,\ldots , a_k\in A$
, there is an
$a_1,\ldots , a_k\in A$
, there is an
![]() $x_{k+1}\not =x_{1},\ldots ,x_{k}$
in G such that
$x_{k+1}\not =x_{1},\ldots ,x_{k}$
in G such that
![]() $R(x_{i},x_{k+1})=a_i$
. This structure was studied as a Fraïssé limit in [Reference Badia and Noguera3].
$R(x_{i},x_{k+1})=a_i$
. This structure was studied as a Fraïssé limit in [Reference Badia and Noguera3].
Since the extension axioms and thus the random model are independent of the probabilities
![]() $\{p_{R}\}_{R\in \tau }$
, we can use Theorem 5 to obtain the following corollary.
$\{p_{R}\}_{R\in \tau }$
, we can use Theorem 5 to obtain the following corollary.
Corollary 7. For any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}$
, the value
$\varphi \in \mathcal {L}^{\boldsymbol {A}}$
, the value
![]() $a\in A$
such that
$a\in A$
such that
![]() $\lim _n \mu _{n}(\varphi =a)= 1$
depends only on
$\lim _n \mu _{n}(\varphi =a)= 1$
depends only on
![]() $\varphi $
and not on the probability distributions
$\varphi $
and not on the probability distributions
![]() $p_{R}$
(provided that
$p_{R}$
(provided that
![]() $p_{R}(a)>0$
for all
$p_{R}(a)>0$
for all
![]() $a\in A)$
.
$a\in A)$
.
We call the value a in Corollary 7 the almost sure or asymptotic truth-value of
![]() $\varphi $
. This corollary entails that assigning the same probability
$\varphi $
. This corollary entails that assigning the same probability
![]() $\frac {1}{|A|}$
to all truth-values has the same effect in the limit as assigning a positive probability to each one.
$\frac {1}{|A|}$
to all truth-values has the same effect in the limit as assigning a positive probability to each one.
Remark 8. If
![]() $p_{R}$
is allowed to take value 0 at some
$p_{R}$
is allowed to take value 0 at some
![]() $a\in A$
, this corresponds to asking the Oberschelp conditions
$a\in A$
, this corresponds to asking the Oberschelp conditions
![]() $\forall x_{1}\ldots \forall x_{n}\,\lnot R^{a}(x_{1},\ldots ,x_{n})$
. Thus, the asympotic value of
$\forall x_{1}\ldots \forall x_{n}\,\lnot R^{a}(x_{1},\ldots ,x_{n})$
. Thus, the asympotic value of
![]() $\varphi $
still exists and depends on the support of
$\varphi $
still exists and depends on the support of
![]() $p_{R}$
only.
$p_{R}$
only.
3.3. Complexity of almost sure values
Grandjean [Reference Grandjean23] showed that the problem of determining for the classical zero-one law if a sentence is almost surely true or not is in PSPACE, and it has been observed [Reference Compton and Rival14] that this holds in the presence of Oberschelp conditions. Moreover, it is PSPACE-complete, even for the vocabulary of pure identity.
Since our translation is exponential in the length of the original formula, it yields only an exponential space upper bound for the computation of the almost sure value of an
![]() $\boldsymbol {A}$
-valued sentence. However, the shape of the translation will allow us to give a simple direct proof of an upper polynomial space bound. PSPACE-completeness will be achieved for logics with crisp identity.
$\boldsymbol {A}$
-valued sentence. However, the shape of the translation will allow us to give a simple direct proof of an upper polynomial space bound. PSPACE-completeness will be achieved for logics with crisp identity.
Theorem 9. For any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, the almost sure value of
$\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
, the almost sure value of
![]() $\varphi $
may be computed in polynomial space.
$\varphi $
may be computed in polynomial space.
We denote by
![]() $Ext_A$
the set of all extension axioms. It is enough to show that for any
$Ext_A$
the set of all extension axioms. It is enough to show that for any
![]() $a\in A$
, it may be determined in polynomial space whether
$a\in A$
, it may be determined in polynomial space whether
![]() $Ext_A\vdash \varphi ^{a}$
. Then, one may check this for each
$Ext_A\vdash \varphi ^{a}$
. Then, one may check this for each
![]() $a\in A$
utilizing the same space until finding the (unique) a for which it holds. Using Grandjean’s strategy [Reference Grandjean23], we can do this without writing
$a\in A$
utilizing the same space until finding the (unique) a for which it holds. Using Grandjean’s strategy [Reference Grandjean23], we can do this without writing
![]() $\varphi ^{a}$
explicitly.
$\varphi ^{a}$
explicitly.
Given a sequence of variables
![]() $\mathbf {x}=x_{1},\ldots ,x_{k}$
, a complete description of
$\mathbf {x}=x_{1},\ldots ,x_{k}$
, a complete description of
![]() $\mathbf {x}$
is a
$\mathbf {x}$
is a
![]() $(\tau \times A)$
-formula
$(\tau \times A)$
-formula
![]() $\Delta (\mathbf {x)}$
of the form
$\Delta (\mathbf {x)}$
of the form
![]() $\bigwedge \nolimits _{\psi \in At_{k}}{\psi }^{f(\psi )}$
where
$\bigwedge \nolimits _{\psi \in At_{k}}{\psi }^{f(\psi )}$
where
![]() $At_{k}$
is the set of atomic
$At_{k}$
is the set of atomic
![]() $\tau $
-formulas with variables in
$\tau $
-formulas with variables in
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $f \colon At_{k} \to A$
. It is easy to see that any such
$f \colon At_{k} \to A$
. It is easy to see that any such
![]() $\Delta (\mathbf {x)}$
is realizable in the classical random model
$\Delta (\mathbf {x)}$
is realizable in the classical random model
![]() $\mathfrak {R}_{\tau \times A}$
, because existential sentences are always almost surely true.
$\mathfrak {R}_{\tau \times A}$
, because existential sentences are always almost surely true.
Notice that, due to the strong homogeneity of
![]() $\mathfrak {R}_{\tau \times A}$
(any isomorphism between finite substructures may be extended to an automorphism, see [Reference Hodges28]), all tuples of
$\mathfrak {R}_{\tau \times A}$
(any isomorphism between finite substructures may be extended to an automorphism, see [Reference Hodges28]), all tuples of
![]() $\mathfrak {R}_{\tau \times A}$
satisfying the same complete description
$\mathfrak {R}_{\tau \times A}$
satisfying the same complete description
![]() $\Delta (\mathbf {x)\ }$
have the same type in
$\Delta (\mathbf {x)\ }$
have the same type in
![]() $\mathfrak {R}_{\tau \times A}$
; therefore, the theory
$\mathfrak {R}_{\tau \times A}$
; therefore, the theory
![]() $Ext_{A}+\Delta (\mathbf {x)}$
is complete for all formulas with their free variables in
$Ext_{A}+\Delta (\mathbf {x)}$
is complete for all formulas with their free variables in
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
In what follows,
![]() $|\alpha |$
will denote the length of a formula or a sequence of variables, or the cardinality of a finite set. For simplicity we assume that the symbols in
$|\alpha |$
will denote the length of a formula or a sequence of variables, or the cardinality of a finite set. For simplicity we assume that the symbols in
![]() $\tau $
and
$\tau $
and
![]() $\tau \times A$
as well as the variables have length
$\tau \times A$
as well as the variables have length
![]() $1$
. Particularly,
$1$
. Particularly,
![]() $|\theta ^{a}|=|\theta |$
for any atomic
$|\theta ^{a}|=|\theta |$
for any atomic
![]() $\theta \in \mathcal {L}_{\tau }^{\boldsymbol {A}}$
and
$\theta \in \mathcal {L}_{\tau }^{\boldsymbol {A}}$
and
![]() $a\in A$
.
$a\in A$
.
Set
![]() $M_{\tau }=\max \{\tau (R):R\in \tau \}$
. Then, it is easy to check that
$M_{\tau }=\max \{\tau (R):R\in \tau \}$
. Then, it is easy to check that
![]() $|\Delta (\mathbf {x)|=}\sum _{R\in \tau }(\tau (R)+c^{\prime })|\mathbf {x}|^{\tau (R)}\leq |\tau |(M_{\tau }+c^{\prime })|\mathbf {x}|^{M_{\tau }}=c|\mathbf {x}|^{M_{\tau }}$
for a suitable constant c.
$|\Delta (\mathbf {x)|=}\sum _{R\in \tau }(\tau (R)+c^{\prime })|\mathbf {x}|^{\tau (R)}\leq |\tau |(M_{\tau }+c^{\prime })|\mathbf {x}|^{M_{\tau }}=c|\mathbf {x}|^{M_{\tau }}$
for a suitable constant c.
Lemma 10. Given a complete description
![]() $\Delta (\mathbf {x})$
, any formula
$\Delta (\mathbf {x})$
, any formula
![]() $\theta \in \mathcal {L}_{\tau }^{\boldsymbol {A}}$
with its free variables contained in
$\theta \in \mathcal {L}_{\tau }^{\boldsymbol {A}}$
with its free variables contained in
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $a\in A$
, it may be decided whether
$a\in A$
, it may be decided whether
![]() $Ext_{A}+\Delta (\mathbf {x})\vdash \theta ^{a}$
or not in space
$Ext_{A}+\Delta (\mathbf {x})\vdash \theta ^{a}$
or not in space
![]() $c(|\mathbf {x}| + |\theta |)^{M_{\tau }}$
.
$c(|\mathbf {x}| + |\theta |)^{M_{\tau }}$
.
Proof. Induction on the complexity of
![]() $\theta $
.
$\theta $
.
-
(1) If
 $\theta $
is atomic, then
$\theta $
is atomic, then
 $Ext_{A}+\Delta (\mathbf {x})\vdash \theta ^{a}$
iff
$Ext_{A}+\Delta (\mathbf {x})\vdash \theta ^{a}$
iff
 $\theta ^{a}$
is a conjunct of
$\theta ^{a}$
is a conjunct of
 $\Delta (\mathbf {x),}$
and this is clearly verifiable in space
$\Delta (\mathbf {x),}$
and this is clearly verifiable in space
 $|\Delta (\mathbf {x)}|+|\theta ^{a}|=|\Delta (\mathbf {x)}|+|\theta |\leq c|\mathbf {x}|^{M_{\tau }}+|\theta |\leq c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
.
$|\Delta (\mathbf {x)}|+|\theta ^{a}|=|\Delta (\mathbf {x)}|+|\theta |\leq c|\mathbf {x}|^{M_{\tau }}+|\theta |\leq c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
. -
(2) If
 $\theta $
is
$\theta $
is
 $\circ (\varphi _{1},\ldots ,\varphi _{k})$
where
$\circ (\varphi _{1},\ldots ,\varphi _{k})$
where
 $\circ $
is a connective, then by definition of the translation and completeness of
$\circ $
is a connective, then by definition of the translation and completeness of
 $Ext_{A} + \Delta (\mathbf {x})$
:
$Ext_{A} + \Delta (\mathbf {x})$
:
 $Ext_{A} + \Delta (\mathbf {x})\vdash \theta ^{a}$
iff there are
$Ext_{A} + \Delta (\mathbf {x})\vdash \theta ^{a}$
iff there are
 $b_{1},\ldots ,b_{k}\in A$
such that
$b_{1},\ldots ,b_{k}\in A$
such that
 $\circ ^{\boldsymbol {A}}(b_{1},\ldots ,b_{k})=a$
and But the k statements in the display may be verified each one in space
$\circ ^{\boldsymbol {A}}(b_{1},\ldots ,b_{k})=a$
and But the k statements in the display may be verified each one in space $$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})\vdash \varphi _{i}^{b_{i}},\text{ for } i=1,\ldots,k. \end{align*} $$
$$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})\vdash \varphi _{i}^{b_{i}},\text{ for } i=1,\ldots,k. \end{align*} $$
 $ c(|\mathbf {x}|+|\theta |)^{M_{\tau }} \geq c(|\mathbf {x}|+|\varphi _{i}|)^{M_{\tau }}$
by induction hypothesis. And we may do this sequentially in the same space for each
$ c(|\mathbf {x}|+|\theta |)^{M_{\tau }} \geq c(|\mathbf {x}|+|\varphi _{i}|)^{M_{\tau }}$
by induction hypothesis. And we may do this sequentially in the same space for each
 $b_{i}$
of each relevant tuple
$b_{i}$
of each relevant tuple
 $b_{1},\ldots ,b_{k}$
, until finding a tuple for which the displayed statement holds.
$b_{1},\ldots ,b_{k}$
, until finding a tuple for which the displayed statement holds.
-
(3) If
 $\theta $
is
$\theta $
is
 $\forall x\,\varphi (x)$
, then by definition of the translation and completeness:
$\forall x\,\varphi (x)$
, then by definition of the translation and completeness:
 $Ext_{A}+\Delta (\mathbf {x})\vdash (\forall x\,\theta (x))^{a}$
iff there are
$Ext_{A}+\Delta (\mathbf {x})\vdash (\forall x\,\theta (x))^{a}$
iff there are
 $b_{1},\ldots ,b_{m}\in A$
such that
$b_{1},\ldots ,b_{m}\in A$
such that
 $b_{1}\wedge \ldots \wedge b_{m}=a$
, and
$b_{1}\wedge \ldots \wedge b_{m}=a$
, and  $$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})\vdash \exists x\,\varphi (x)^{b_{1}},\ldots,\exists x\,\varphi (x)^{b_{m}},\forall x\,(\bigvee_{b\geq a}\varphi (x)^{b}), \end{align*} $$
$$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})\vdash \exists x\,\varphi (x)^{b_{1}},\ldots,\exists x\,\varphi (x)^{b_{m}},\forall x\,(\bigvee_{b\geq a}\varphi (x)^{b}), \end{align*} $$
equivalently,
 $$ \begin{align*} Ext_{A}+\Delta (\mathbf{x}) &\quad\vdash\quad \exists x\,\varphi (x)^{b_{i}},\text{ for }i=1,\ldots,m \\ Ext_{A}+\Delta (\mathbf{x}) &\quad\not\vdash\quad \exists x\,\varphi (x)^{b},\text{ for all }b\not\geq a \end{align*} $$
$$ \begin{align*} Ext_{A}+\Delta (\mathbf{x}) &\quad\vdash\quad \exists x\,\varphi (x)^{b_{i}},\text{ for }i=1,\ldots,m \\ Ext_{A}+\Delta (\mathbf{x}) &\quad\not\vdash\quad \exists x\,\varphi (x)^{b},\text{ for all }b\not\geq a \end{align*} $$
because
 $\forall x\,(\bigvee _{b\geq a}\varphi (x)^{b})$
is equivalent in
$\forall x\,(\bigvee _{b\geq a}\varphi (x)^{b})$
is equivalent in
 $Ext_{A}$
to
$Ext_{A}$
to
 $\bigwedge \nolimits _{b\not \geq a}\lnot \exists x\,\varphi (x)^{b}$
, and
$\bigwedge \nolimits _{b\not \geq a}\lnot \exists x\,\varphi (x)^{b}$
, and
 $Ext_{A}+\Delta (\mathbf {x})\vdash \lnot \exists x\,\varphi (x)^{b}$
iff
$Ext_{A}+\Delta (\mathbf {x})\vdash \lnot \exists x\,\varphi (x)^{b}$
iff
 $Ext_{A}+\Delta (\mathbf {x})\not \vdash \exists x\,\varphi (x)^{b}$
due to completeness. Now,
$Ext_{A}+\Delta (\mathbf {x})\not \vdash \exists x\,\varphi (x)^{b}$
due to completeness. Now,
 $Ext_{A}+\Delta (\mathbf {x})\vdash \exists x\,\varphi (x)^{b_{1}}$
if and only if there is an expansion
$Ext_{A}+\Delta (\mathbf {x})\vdash \exists x\,\varphi (x)^{b_{1}}$
if and only if there is an expansion
 $\Delta ^{\prime }(x,\mathbf {x})$
of
$\Delta ^{\prime }(x,\mathbf {x})$
of
 $\Delta (\mathbf {x})$
such that
$\Delta (\mathbf {x})$
such that  $$ \begin{align*} Ext_{A}+\Delta ^{\prime }(x,\mathbf{x})\vdash \varphi (x)^{b_{1}}, \end{align*} $$
$$ \begin{align*} Ext_{A}+\Delta ^{\prime }(x,\mathbf{x})\vdash \varphi (x)^{b_{1}}, \end{align*} $$
(if
 $\mathbf {a}$
is a tuple in
$\mathbf {a}$
is a tuple in
 $\mathfrak {R}_{\tau \times A}$
satisfying
$\mathfrak {R}_{\tau \times A}$
satisfying
 $\Delta (\mathbf {x})$
and b is a witness of
$\Delta (\mathbf {x})$
and b is a witness of
 $\exists x\,\varphi (x,\mathbf {a})^{b_{1}}$
, then the complete description
$\exists x\,\varphi (x,\mathbf {a})^{b_{1}}$
, then the complete description
 $\Delta ^{\prime }(x,\mathbf {x})$
of
$\Delta ^{\prime }(x,\mathbf {x})$
of
 $\mathfrak {R}_{\tau \times A}\upharpoonright \{b,\mathbf {a}\}$
does the job
$\mathfrak {R}_{\tau \times A}\upharpoonright \{b,\mathbf {a}\}$
does the job
 $)$
. By induction hypothesis, we may check this for each possible expansion of
$)$
. By induction hypothesis, we may check this for each possible expansion of
 $\Delta (\mathbf {x})$
in space
$\Delta (\mathbf {x})$
in space
 $c(|\mathbf {x}|+1+|\varphi (x)|)^{M_{\tau }}\leq c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
. Doing this sequentially in the same space for each
$c(|\mathbf {x}|+1+|\varphi (x)|)^{M_{\tau }}\leq c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
. Doing this sequentially in the same space for each
 $b_{1},\ldots ,b_{m}, b$
such that
$b_{1},\ldots ,b_{m}, b$
such that
 $b_{1}\wedge \ldots \wedge b_{m}=a$
and
$b_{1}\wedge \ldots \wedge b_{m}=a$
and
 $b\not \geq a$
, we may check whether
$b\not \geq a$
, we may check whether
 $Ext_{A}+\Delta (\mathbf {x})\vdash (\forall x\,\theta (x))^{a}$
.
$Ext_{A}+\Delta (\mathbf {x})\vdash (\forall x\,\theta (x))^{a}$
. -
(4) If
 $\theta $
is
$\theta $
is
 $\exists x\,\varphi (x)$
, then, similarly to the previous case,
$\exists x\,\varphi (x)$
, then, similarly to the previous case,
 $Ext_{A}+\Delta (\mathbf {x})\vdash (\exists x\,\varphi (x))^{a}$
iff there are
$Ext_{A}+\Delta (\mathbf {x})\vdash (\exists x\,\varphi (x))^{a}$
iff there are
 $b_{1},\ldots ,b_{m}\in A$
such that
$b_{1},\ldots ,b_{m}\in A$
such that
 $b_{1}\vee \ldots \vee b_{m}=a$
, and
$b_{1}\vee \ldots \vee b_{m}=a$
, and  $$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})&\quad\vdash\quad \exists x\,\varphi (x)^{b_{i}},\text{ for }i=1,\dots,m \\ Ext_{A}+\Delta (\mathbf{x}) &\quad\not\vdash\quad \exists x\,\varphi (x)^{b},\text{ for all }b\not\leq a \end{align*} $$
$$ \begin{align*} Ext_{A}+\Delta (\mathbf{x})&\quad\vdash\quad \exists x\,\varphi (x)^{b_{i}},\text{ for }i=1,\dots,m \\ Ext_{A}+\Delta (\mathbf{x}) &\quad\not\vdash\quad \exists x\,\varphi (x)^{b},\text{ for all }b\not\leq a \end{align*} $$
and this claim may be verified in space
 $c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
.
$c(|\mathbf {x}|+|\theta |)^{M_{\tau }}$
.
Corollary 11. The almost sure value of any sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
may be computed in space
$\varphi \in \mathcal {L}^{\boldsymbol {A}}(\tau )$
may be computed in space
![]() $c(1+|\varphi |)^{M_{\tau }}$
.
$c(1+|\varphi |)^{M_{\tau }}$
.
Proof. Let
![]() $\Delta (x)$
be any complete description in one variable. Then,
$\Delta (x)$
be any complete description in one variable. Then,
![]() $Ext_{A}\vdash \varphi ^{a}$
iff
$Ext_{A}\vdash \varphi ^{a}$
iff
![]() $Ext_{A}+\exists x\Delta (x)\vdash \varphi ^{a}$
(because
$Ext_{A}+\exists x\Delta (x)\vdash \varphi ^{a}$
(because
![]() $Ext_{A}\vdash \exists x\,\Delta (x))$
iff
$Ext_{A}\vdash \exists x\,\Delta (x))$
iff
![]() $Ext_{A}+\Delta (x)\vdash \varphi ^{a}$
. Thus,
$Ext_{A}+\Delta (x)\vdash \varphi ^{a}$
. Thus,
![]() $Ext_{A}\vdash \varphi ^{a}$
may be decided in space
$Ext_{A}\vdash \varphi ^{a}$
may be decided in space
![]() $c(1+|\varphi |)^{M_{\tau }}$
. Check this for any
$c(1+|\varphi |)^{M_{\tau }}$
. Check this for any
![]() $a\in A$
until finding the only a for which it holds.
$a\in A$
until finding the only a for which it holds.
If the logic satisfies additional Oberschelp conditions in the translation (besides the necessary ones), the previous result is obtained by considering only complete descriptions compatible with those conditions.
![]() $\boldsymbol {A}$
-valued logic with crisp identity, in symbols
$\boldsymbol {A}$
-valued logic with crisp identity, in symbols
![]() $\mathcal {L}_{\approx }^{\boldsymbol {A}}$
, will be
$\mathcal {L}_{\approx }^{\boldsymbol {A}}$
, will be
![]() $\mathcal {L}^{\boldsymbol {A}}$
enriched with a distinguished binary relation symbol
$\mathcal {L}^{\boldsymbol {A}}$
enriched with a distinguished binary relation symbol
![]() $\approx $
interpreted in each model as the characteristic function of the diagonal.
$\approx $
interpreted in each model as the characteristic function of the diagonal.
This corresponds to having the Oberschelp conditions
![]() $\forall x\,(x\approx ^{1}x)$
,
$\forall x\,(x\approx ^{1}x)$
,
![]() $\forall ^{\not =}xy\,(x\approx ^{0}y)$
in the translated logic. Hence, this logic has a zero-one law and satisfies the above results.
$\forall ^{\not =}xy\,(x\approx ^{0}y)$
in the translated logic. Hence, this logic has a zero-one law and satisfies the above results.
Theorem 12. If
![]() $\boldsymbol {A}$
has a term u such that
$\boldsymbol {A}$
has a term u such that
![]() $u^{\boldsymbol {A}}(1)=0$
and
$u^{\boldsymbol {A}}(1)=0$
and
![]() $u^{\boldsymbol {A}}(0)=1$
, then computing the almost sure values of sentences of
$u^{\boldsymbol {A}}(0)=1$
, then computing the almost sure values of sentences of
![]() $\mathcal {L}_{\approx }^{\boldsymbol {A}}$
is PSPACE-complete.
$\mathcal {L}_{\approx }^{\boldsymbol {A}}$
is PSPACE-complete.
Proof. Consider the translation
![]() $\varphi \longmapsto \widehat {\varphi }$
from classical pure identity logic into
$\varphi \longmapsto \widehat {\varphi }$
from classical pure identity logic into
![]() $\mathcal {L}_{\approx }^{\boldsymbol {A}}$
that sends
$\mathcal {L}_{\approx }^{\boldsymbol {A}}$
that sends
![]() $=$
to
$=$
to
![]() $\approx $
and
$\approx $
and
![]() $\lnot $
to u. A straightforward induction on the complexity of
$\lnot $
to u. A straightforward induction on the complexity of
![]() $\varphi $
shows that, for any
$\varphi $
shows that, for any
![]() $\mathbf {m}$
in
$\mathbf {m}$
in
![]() $\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
,
$\mathfrak {R}_{\tau }^{\boldsymbol {A}}$
,
![]() $||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}(\mathbf {m})\in \{0,1\}$
and
$||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}(\mathbf {m})\in \{0,1\}$
and
![]() $||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}(\mathbf {m})=1$
iff
$||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}(\mathbf {m})=1$
iff
![]() $\mathfrak {R}_{\tau \times A}\models \varphi [ \mathbf {m}]$
. Notice that for the classical random model of the extension axioms of this logic:
$\mathfrak {R}_{\tau \times A}\models \varphi [ \mathbf {m}]$
. Notice that for the classical random model of the extension axioms of this logic:
![]() $\mathfrak {R}_{\tau \times A}\models m\approx ^{1}n$
iff
$\mathfrak {R}_{\tau \times A}\models m\approx ^{1}n$
iff
![]() $m=n$
,
$m=n$
,
![]() $\mathfrak {R}_{\tau \times A}\models m\approx ^{0}n\,$
iff
$\mathfrak {R}_{\tau \times A}\models m\approx ^{0}n\,$
iff
![]() $m\not =n$
. Therefore, for any classical identity sentence
$m\not =n$
. Therefore, for any classical identity sentence
![]() $\varphi $
,
$\varphi $
,
![]() $\lim _n\mu _{n}(\widehat {\varphi }=1)= 1$
iff
$\lim _n\mu _{n}(\widehat {\varphi }=1)= 1$
iff
![]() $||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=1$
iff
$||\widehat {\varphi }||^{\mathfrak {R}_{\tau }^{\boldsymbol {A}}}=1$
iff
![]() $Ext_{A}\vdash \varphi $
iff
$Ext_{A}\vdash \varphi $
iff
![]() $I_{\infty }\vdash \varphi $
, where
$I_{\infty }\vdash \varphi $
, where
![]() $I_{\infty }$
is the theory of identity in infinite sets. But deducibility in the latter theory is PSPACE-hard by results of Stockmeyer [Reference Stockmeyer38].
$I_{\infty }$
is the theory of identity in infinite sets. But deducibility in the latter theory is PSPACE-hard by results of Stockmeyer [Reference Stockmeyer38].
4. The set of almost sure values in finitely valued predicate logics
Call
![]() $a\in A$
an almost sure truth-value of
$a\in A$
an almost sure truth-value of
![]() $\mathcal {L}^{\boldsymbol {A}}$
(of
$\mathcal {L}^{\boldsymbol {A}}$
(of
![]() $\boldsymbol {A}$
) if there is a sentence
$\boldsymbol {A}$
) if there is a sentence
![]() $\varphi \in \mathcal {L}^{\boldsymbol {A}}$
such that
$\varphi \in \mathcal {L}^{\boldsymbol {A}}$
such that
![]() $\lim _n\mu _{n}(\varphi =a)=1$
. Do all the elements of A arise as almost sure values? If not, which are those values? We will see that for many familiar classes of finite algebras the answer to the first question is positive (for example
$\lim _n\mu _{n}(\varphi =a)=1$
. Do all the elements of A arise as almost sure values? If not, which are those values? We will see that for many familiar classes of finite algebras the answer to the first question is positive (for example
![]() $\mathrm {MV}$
-chains for Łukasiewicz logic, or
$\mathrm {MV}$
-chains for Łukasiewicz logic, or
![]() $\mathrm {G}$
-chains for Gödel logic), for others have a small subset of almost sure values (
$\mathrm {G}$
-chains for Gödel logic), for others have a small subset of almost sure values (
![]() $0$
or
$0$
or
![]() $1$
for Boolean algebras, at most four values for De Morgan algebras, at most three for the lattice-negation reducts of G-chains, etc.).
$1$
for Boolean algebras, at most four values for De Morgan algebras, at most three for the lattice-negation reducts of G-chains, etc.).
The first assertion follows from the following general lemma.
Lemma 13. Let
![]() $t(v_{1},\ldots ,v_{k})$
be a term in the signature of a finite lattice algebra
$t(v_{1},\ldots ,v_{k})$
be a term in the signature of a finite lattice algebra
![]() $\boldsymbol {A}$
, then
$\boldsymbol {A}$
, then
![]() $m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
$m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
![]() $s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure truth-values of
$s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure truth-values of
![]() $\mathcal {L}^{\boldsymbol {A}}$
.
$\mathcal {L}^{\boldsymbol {A}}$
.
Proof. Let
![]() $R(x)$
be an atomic formula with a single variable x. We show that
$R(x)$
be an atomic formula with a single variable x. We show that
Fix tuples
![]() ${\langle {a_{j}^{1}}\rangle }_{j},\ldots ,{\langle {a_{j}^{\ell }}\rangle }_{j}\in |A|^{k}$
, such that
${\langle {a_{j}^{1}}\rangle }_{j},\ldots ,{\langle {a_{j}^{\ell }}\rangle }_{j}\in |A|^{k}$
, such that
![]() $t^{\boldsymbol {A}}(a_{1}^{1},\ldots ,a_{k}^{1})\wedge ^{\boldsymbol {A}}\ldots \wedge ^{\boldsymbol {A}}t^{\boldsymbol {A}}(a_{1}^{\ell },\ldots ,a_{k}^{\ell })=m,$
and for each
$t^{\boldsymbol {A}}(a_{1}^{1},\ldots ,a_{k}^{1})\wedge ^{\boldsymbol {A}}\ldots \wedge ^{\boldsymbol {A}}t^{\boldsymbol {A}}(a_{1}^{\ell },\ldots ,a_{k}^{\ell })=m,$
and for each
![]() $n\geq k\ell $
find
$n\geq k\ell $
find
![]() $K\subseteq [ n]^{k}$
of cardinal
$K\subseteq [ n]^{k}$
of cardinal
![]() $|K|=\lfloor n/k\ell \rfloor $
such that all tuples in K have all their components distinct, and two different tuples in K are distinct at each coordinate. Then,
$|K|=\lfloor n/k\ell \rfloor $
such that all tuples in K have all their components distinct, and two different tuples in K are distinct at each coordinate. Then,
 $$ \begin{align*} &\quad \mu _{n}(\forall x_{1}\ldots\forall x_{k}\,t(R(x_{1}),\ldots,R(x_{k}))=m)\\ &\quad =\Pr_{n}(\inf_{i_{1},\ldots,i_{k}\in [ n]}t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))=m)\\ &\quad \geq \Pr_{n}\ (\text{for some } {\langle {i_{j}^{1}}\rangle}_{j},\ldots,{\langle {i_{j}^{\ell}}\rangle}_{j} \text{ in } [n]^{k}:R(i_{j}^{i})=a_{j}^{i}, \text{ for } i=1,\ldots,\ell , j=1,\ldots,k)\\ &\quad \geq \Pr_{n}\ (\text{for some }{\langle{i_{j}^{1}}\rangle}_{j},\ldots,{\langle{i_{j}^{\ell}}\rangle}_{j} \text{ in } K:R(i_{j}^{i})=a_{j}^{i}, \text{ for } i=1,\ldots,\ell , j= 1,\ldots,k)\\ &\quad =1-\Pr_{n}\ (\text{for all } {\langle {i_{j}^{1}}\rangle}_{j},\ldots,{\langle {i_{j}^{\ell}}\rangle}_{j} \text{ in } K \text{ is false: } R(i_{j}^{i})=a_{j}^{i},\\ &\qquad\qquad\text{ for } i=1,\ldots,\ell, j=1,\ldots,k)\\ &\quad =1-\prod\nolimits_{{\langle {i_{1}^{1},\ldots, i_{k}^{1}}\rangle},\ldots,{\langle {i_{1}^{\ell},\ldots, i_{k}^{\ell}}\rangle} \in K}[1-\Pr_{n}(R(i_{j}^{i})=a_{j}^{i} \text{ for } i=1,\ldots,\ell, j=1,\ldots,k))]\\ &\quad =1-(1-p_{R}(a_{1}^{1})\ldots p_{R}(a_{k}^{\ell }))^{\lfloor n/k\ell \rfloor}. \end{align*} $$
$$ \begin{align*} &\quad \mu _{n}(\forall x_{1}\ldots\forall x_{k}\,t(R(x_{1}),\ldots,R(x_{k}))=m)\\ &\quad =\Pr_{n}(\inf_{i_{1},\ldots,i_{k}\in [ n]}t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))=m)\\ &\quad \geq \Pr_{n}\ (\text{for some } {\langle {i_{j}^{1}}\rangle}_{j},\ldots,{\langle {i_{j}^{\ell}}\rangle}_{j} \text{ in } [n]^{k}:R(i_{j}^{i})=a_{j}^{i}, \text{ for } i=1,\ldots,\ell , j=1,\ldots,k)\\ &\quad \geq \Pr_{n}\ (\text{for some }{\langle{i_{j}^{1}}\rangle}_{j},\ldots,{\langle{i_{j}^{\ell}}\rangle}_{j} \text{ in } K:R(i_{j}^{i})=a_{j}^{i}, \text{ for } i=1,\ldots,\ell , j= 1,\ldots,k)\\ &\quad =1-\Pr_{n}\ (\text{for all } {\langle {i_{j}^{1}}\rangle}_{j},\ldots,{\langle {i_{j}^{\ell}}\rangle}_{j} \text{ in } K \text{ is false: } R(i_{j}^{i})=a_{j}^{i},\\ &\qquad\qquad\text{ for } i=1,\ldots,\ell, j=1,\ldots,k)\\ &\quad =1-\prod\nolimits_{{\langle {i_{1}^{1},\ldots, i_{k}^{1}}\rangle},\ldots,{\langle {i_{1}^{\ell},\ldots, i_{k}^{\ell}}\rangle} \in K}[1-\Pr_{n}(R(i_{j}^{i})=a_{j}^{i} \text{ for } i=1,\ldots,\ell, j=1,\ldots,k))]\\ &\quad =1-(1-p_{R}(a_{1}^{1})\ldots p_{R}(a_{k}^{\ell }))^{\lfloor n/k\ell \rfloor}. \end{align*} $$
For the last two identities, we use that the
![]() $k\ell $
events
$k\ell $
events
![]() $R(i_{j}^{i})=a_{j}^{i}$
form a mutually independent set for distinct
$R(i_{j}^{i})=a_{j}^{i}$
form a mutually independent set for distinct
![]() $i_{1}^{1},\ldots , i_{k}^{1},\ldots ,i_{1}^{\ell },\ldots , i_{k}^{\ell }\in K$
. Since
$i_{1}^{1},\ldots , i_{k}^{1},\ldots ,i_{1}^{\ell },\ldots , i_{k}^{\ell }\in K$
. Since
![]() $p_{R}(a_{i}^{j})>0$
, the last quantity converges to
$p_{R}(a_{i}^{j})>0$
, the last quantity converges to
![]() $1$
. A similar proof shows that
$1$
. A similar proof shows that
Example 14. It follows that
![]() $0$
and
$0$
and
![]() $1$
are always almost sure values, even if they do not appear in the signature of A, because they are inf and sup of the term
$1$
are always almost sure values, even if they do not appear in the signature of A, because they are inf and sup of the term
![]() $t(v):=v$
.
$t(v):=v$
.
Example 15. Let
![]() ${\mathrm {L}}_{N+1}={\langle {\{0,\frac {1}{N},\ldots ,\frac {N-1}{N},1\},\wedge ,\vee ,\lnot ,\rightarrow }\rangle }$
be the
${\mathrm {L}}_{N+1}={\langle {\{0,\frac {1}{N},\ldots ,\frac {N-1}{N},1\},\wedge ,\vee ,\lnot ,\rightarrow }\rangle }$
be the
![]() $\mathrm {MV}$
-chain of
$\mathrm {MV}$
-chain of
![]() $N+1$
elements, where
$N+1$
elements, where
![]() $\wedge ,\vee $
, are
$\wedge ,\vee $
, are
![]() $\min $
and
$\min $
and
![]() $\max $
, and
$\max $
, and
![]() $\lnot ,\rightarrow $
are Łukasiewicz negation and implication. Then all values of
$\lnot ,\rightarrow $
are Łukasiewicz negation and implication. Then all values of
![]() ${\mathrm {L}}_{N+1}$
are almost sure values of the corresponding predicate logic. To see this, notice that using (Chang) connectives:
${\mathrm {L}}_{N+1}$
are almost sure values of the corresponding predicate logic. To see this, notice that using (Chang) connectives:
![]() $a\oplus b:=\lnot a\rightarrow b$
,
$a\oplus b:=\lnot a\rightarrow b$
,
![]() $a\odot b:=\lnot (a\rightarrow \lnot b)$
,
$a\odot b:=\lnot (a\rightarrow \lnot b)$
,
![]() $na:=a\oplus \ldots \oplus a$
,
$na:=a\oplus \ldots \oplus a$
,
![]() $a^{n}:=a\odot \ldots \odot a$
$a^{n}:=a\odot \ldots \odot a$
![]() $(n\geq 1)$
, the term
$(n\geq 1)$
, the term
![]() $t(v)=v^{N}\oplus \lnot v$
has minimum value
$t(v)=v^{N}\oplus \lnot v$
has minimum value
![]() $\frac {1}{N}$
in
$\frac {1}{N}$
in
![]() ${\mathrm {L}}_{N+1}$
(taken at
${\mathrm {L}}_{N+1}$
(taken at
![]() $a=\frac {N-1}{N})$
, and thus
$a=\frac {N-1}{N})$
, and thus
![]() $t_{k/N}(v)=k(v^{N}\oplus \lnot v)=v^{k}\rightarrow kv^{N} $
has minimum value
$t_{k/N}(v)=k(v^{N}\oplus \lnot v)=v^{k}\rightarrow kv^{N} $
has minimum value
![]() $\frac {k}{N}$
.
$\frac {k}{N}$
.
Example 16. Let
![]() $\boldsymbol {G}_{N+1}={\langle {\{0=g_{0}<\ldots <g_{N}=1\},\wedge ,\vee ,\lnot ,\rightarrow }\rangle }$
be the G-chain of
$\boldsymbol {G}_{N+1}={\langle {\{0=g_{0}<\ldots <g_{N}=1\},\wedge ,\vee ,\lnot ,\rightarrow }\rangle }$
be the G-chain of
![]() $N+1$
elements, where
$N+1$
elements, where
![]() $\lnot ,\rightarrow $
are Gödel implication and negation, then all values of
$\lnot ,\rightarrow $
are Gödel implication and negation, then all values of
![]() $\boldsymbol {G}_{N+1}$
are almost sure values of the corresponding predicate logic. Define:
$\boldsymbol {G}_{N+1}$
are almost sure values of the corresponding predicate logic. Define:
 $$ \begin{align*} &t_{1}(v_{1}):=v_{1}\vee \lnot v_{1}, t_{k+1}(v_{1},\ldots,v_{k+1}):=v_{k+1}\vee (v_{k+1}\rightarrow t_{k}(v_{1},\ldots,v_{k}))\\ &\qquad \qquad =v_{k+1}\vee (v_{k+1}\rightarrow (v_{k}\vee (v_{k}\rightarrow \ldots\rightarrow (v_{2}\vee (v_{2}\rightarrow (v_{1}\vee \lnot v_{1}))\ldots))) \end{align*} $$
$$ \begin{align*} &t_{1}(v_{1}):=v_{1}\vee \lnot v_{1}, t_{k+1}(v_{1},\ldots,v_{k+1}):=v_{k+1}\vee (v_{k+1}\rightarrow t_{k}(v_{1},\ldots,v_{k}))\\ &\qquad \qquad =v_{k+1}\vee (v_{k+1}\rightarrow (v_{k}\vee (v_{k}\rightarrow \ldots\rightarrow (v_{2}\vee (v_{2}\rightarrow (v_{1}\vee \lnot v_{1}))\ldots))) \end{align*} $$
then the minimum possible value of
![]() $t_{1}(v_{1})$
in
$t_{1}(v_{1})$
in
![]() $\boldsymbol {G}_{N+1}$
is
$\boldsymbol {G}_{N+1}$
is
![]() $g_{1}\vee \lnot g_{1}=g_{1},$
since
$g_{1}\vee \lnot g_{1}=g_{1},$
since
![]() $g_{0}\vee \lnot g_{0} =1$
and
$g_{0}\vee \lnot g_{0} =1$
and
![]() $g_{j}\vee \lnot g_{j}=g_{j}$
for
$g_{j}\vee \lnot g_{j}=g_{j}$
for
![]() $g_{j}>g_{1}$
. For
$g_{j}>g_{1}$
. For
![]() $2\leq k\leq N$
:
$2\leq k\leq N$
:
obtained at
![]() $g_{1},\ldots ,g_{k},$
because
$g_{1},\ldots ,g_{k},$
because
 $$ \begin{align*} t_{k}(x_{1},\ldots,x_{k})=\left\{ \begin{array}{cc} 1 & \text{ if }x_{i+1}\leq x_{i}\text{ for some }i \\ x_{k} & \text{ if }x_{i}<x_{i+1}\text{ for all }i. \end{array} \right. \end{align*} $$
$$ \begin{align*} t_{k}(x_{1},\ldots,x_{k})=\left\{ \begin{array}{cc} 1 & \text{ if }x_{i+1}\leq x_{i}\text{ for some }i \\ x_{k} & \text{ if }x_{i}<x_{i+1}\text{ for all }i. \end{array} \right. \end{align*} $$
Remark 17. Notice that in the proof of Lemma 13, we have used a single predicate symbol and k variables to write the sentences
 $$ \begin{align*} &\forall x\, t(P_{1}(x),..,P_{k}(x))\\ &\exists x\, t(P_{1}(x),..,P_{k}(x)) \end{align*} $$
$$ \begin{align*} &\forall x\, t(P_{1}(x),..,P_{k}(x))\\ &\exists x\, t(P_{1}(x),..,P_{k}(x)) \end{align*} $$
having the desired almost sure values m and s. We may use instead k (unary) predicates and a single variable with a similar proof. Therefore, via the translation explained in Remark 4, the formulas
![]() $\square t(p_{1},\ldots ,p_{k})$
and
$\square t(p_{1},\ldots ,p_{k})$
and
![]() $\Diamond t(p_{1},\ldots ,p_{k})$
of the S
$\Diamond t(p_{1},\ldots ,p_{k})$
of the S
![]() $5_{c}^{A}$
have almost sure values m and
$5_{c}^{A}$
have almost sure values m and
![]() $s,$
respectively
$s,$
respectively
![]() $.$
It follows then from Example 15 that all values of
$.$
It follows then from Example 15 that all values of
![]() ${\mathrm {L}}_{N+1}$
are almost sure values of S
${\mathrm {L}}_{N+1}$
are almost sure values of S
![]() $5_{c}^{{\mathrm {L}}_{N+1}}$
, since the formula
$5_{c}^{{\mathrm {L}}_{N+1}}$
, since the formula
![]() $\square (p^{k}\rightarrow kp^{N})$
has almost sure value
$\square (p^{k}\rightarrow kp^{N})$
has almost sure value
![]() $\frac {k}{N},$
and it follows, from Example 16, that all values of G
$\frac {k}{N},$
and it follows, from Example 16, that all values of G
![]() $_{N+1}$
are almost sure values of S
$_{N+1}$
are almost sure values of S
![]() $5_{c}^{G_{N+1}},$
since the modal formula
$5_{c}^{G_{N+1}},$
since the modal formula
![]() $\square (p_{k}\vee (p_{k}\rightarrow (p_{k-1}\vee (p_{k-1}\rightarrow (\ldots (p_{1}\vee \lnot p_{1})\ldots ))$
takes the almost sure value
$\square (p_{k}\vee (p_{k}\rightarrow (p_{k-1}\vee (p_{k-1}\rightarrow (\ldots (p_{1}\vee \lnot p_{1})\ldots ))$
takes the almost sure value
![]() $g_{k}$
.
$g_{k}$
.
We turn now to algebras with few almost sure values and obtain the following result inspired by the techniques in [Reference Grädel, Helal, Naaf, Wilke, Baier and Fisman22]. Notice that the proof of this theorem actually gives a new proof of the zero-one law in the cases considered.
Theorem 18. Let
![]() $\boldsymbol {A}={\langle {A,\wedge ,\vee ,\lnot }\rangle }$
be a finite distributive lattice with a negation satisfying:
$\boldsymbol {A}={\langle {A,\wedge ,\vee ,\lnot }\rangle }$
be a finite distributive lattice with a negation satisfying:
-
(1)
 $\lnot (v\wedge w)=\lnot v\vee \lnot w$
,
$\lnot (v\wedge w)=\lnot v\vee \lnot w$
,
 $\lnot (v\vee w)=\lnot v\wedge \lnot w$
$\lnot (v\vee w)=\lnot v\wedge \lnot w$
-
(2)
 $v\leq \lnot \lnot v$
$v\leq \lnot \lnot v$
-
(3)
 $\lnot 1=0$
.
$\lnot 1=0$
.
Then, the almost sure values of
![]() $\mathcal {L}^{\boldsymbol {A}}$
are
$\mathcal {L}^{\boldsymbol {A}}$
are
![]() $0$
,
$0$
,
![]() $\varepsilon ,\varepsilon ^{\prime },\delta ,\delta ^{\prime }\!$
, and
$\varepsilon ,\varepsilon ^{\prime },\delta ,\delta ^{\prime }\!$
, and
![]() $1$
, where
$1$
, where
 $$ \begin{align*} &\varepsilon =\sup\nolimits_{x\in A}(x\wedge \lnot x), \varepsilon ^{\prime}=\sup\nolimits_{x\in A}(\lnot x\wedge \lnot \lnot x),\,\\ &\delta =\inf\nolimits_{x\in A}(x\vee \lnot x), \delta ^{\prime}=\inf\nolimits_{x\in A}(\lnot x\vee \lnot \lnot x). \end{align*} $$
$$ \begin{align*} &\varepsilon =\sup\nolimits_{x\in A}(x\wedge \lnot x), \varepsilon ^{\prime}=\sup\nolimits_{x\in A}(\lnot x\wedge \lnot \lnot x),\,\\ &\delta =\inf\nolimits_{x\in A}(x\vee \lnot x), \delta ^{\prime}=\inf\nolimits_{x\in A}(\lnot x\vee \lnot \lnot x). \end{align*} $$
Proof. We already know these values are almost sure by Lemma 13. In order to see that they are the only ones, notice first the following derived laws of
![]() $\boldsymbol {A}$
:
$\boldsymbol {A}$
:
-
(4)
 $v\leq w$
implies
$v\leq w$
implies
 $\lnot w\leq \lnot v$
$\lnot w\leq \lnot v$
-
(5)
 $\lnot \lnot \lnot v=\lnot v$
$\lnot \lnot \lnot v=\lnot v$
-
(6)
 $\lnot 0=\lnot \lnot 1=1$
,
$\lnot 0=\lnot \lnot 1=1$
,
 $\lnot \lnot 0=0$
.
$\lnot \lnot 0=0$
. -
(7)
 $0\leq \varepsilon \leq \varepsilon ^{\prime }\leq \delta \leq \delta ^{\prime }\leq 1$
,
$0\leq \varepsilon \leq \varepsilon ^{\prime }\leq \delta \leq \delta ^{\prime }\leq 1$
,
 $\lnot \varepsilon =\lnot \varepsilon ^{\prime }=\delta ^{\prime }$
,
$\lnot \varepsilon =\lnot \varepsilon ^{\prime }=\delta ^{\prime }$
,
 $\lnot \delta =\lnot \delta ^{\prime }=\varepsilon ^{\prime },$
thus
$\lnot \delta =\lnot \delta ^{\prime }=\varepsilon ^{\prime },$
thus
 $E=\{0,\varepsilon ,\varepsilon ^{\prime }, \delta ,\delta ^{\prime },1\} $
is a subalgebra of
$E=\{0,\varepsilon ,\varepsilon ^{\prime }, \delta ,\delta ^{\prime },1\} $
is a subalgebra of
 $\boldsymbol {A}$
.
$\boldsymbol {A}$
.
Expand
![]() $\boldsymbol {A}$
to the algebra
$\boldsymbol {A}$
to the algebra
![]() $\boldsymbol {A}^{+}={\langle {A,\wedge ,\vee ,\lnot ,0,\varepsilon ,\varepsilon ^{\prime },\delta ,\delta ^{\prime },1}\rangle }$
and use the same symbols in the signature to denote the constants in E. By distributivity, (1), (5), (6), and (7), any term
$\boldsymbol {A}^{+}={\langle {A,\wedge ,\vee ,\lnot ,0,\varepsilon ,\varepsilon ^{\prime },\delta ,\delta ^{\prime },1}\rangle }$
and use the same symbols in the signature to denote the constants in E. By distributivity, (1), (5), (6), and (7), any term
![]() $t(v_{1},\ldots ,v_{k})$
in the signature of
$t(v_{1},\ldots ,v_{k})$
in the signature of
![]() $\boldsymbol {A}^{+}$
may be put in disjunctive normal form:
$\boldsymbol {A}^{+}$
may be put in disjunctive normal form:
![]() $\bigvee \nolimits _{s}C_{s}$
with
$\bigvee \nolimits _{s}C_{s}$
with
![]() $C_{s}=e\wedge \bigwedge \nolimits _{r}\lnot ^{n_{r}}v_{i_{r}},$
where
$C_{s}=e\wedge \bigwedge \nolimits _{r}\lnot ^{n_{r}}v_{i_{r}},$
where
![]() $e\in E$
,
$e\in E$
,
![]() $v_{i_{r}}\in \{v_{1},\ldots ,v_{k}\}$
and
$v_{i_{r}}\in \{v_{1},\ldots ,v_{k}\}$
and
![]() $n_{r}\leq 2$
. Moreover, by (2), we may assume no pair
$n_{r}\leq 2$
. Moreover, by (2), we may assume no pair
![]() $\{v_{i},\lnot \lnot v_{i}\}$
appears in
$\{v_{i},\lnot \lnot v_{i}\}$
appears in
![]() $C_{s}$
, since
$C_{s}$
, since
![]() $v_{i}\wedge \lnot \lnot v_{i}=v_{i}$
. By idempotency and commutativity of
$v_{i}\wedge \lnot \lnot v_{i}=v_{i}$
. By idempotency and commutativity of
![]() $\wedge $
, we may assume that each variable appears at most once in
$\wedge $
, we may assume that each variable appears at most once in
![]() $C_{s}$
as:
$C_{s}$
as:
![]() $v_{i}$
,
$v_{i}$
,
![]() $\lnot v_{i},$
or
$\lnot v_{i},$
or
![]() $\lnot \lnot v_{i},$
or at most twice as:
$\lnot \lnot v_{i},$
or at most twice as:
![]() $v_{i}\wedge \lnot v_{i},$
or
$v_{i}\wedge \lnot v_{i},$
or
![]() $\lnot v_{i}\wedge \lnot \lnot v_{i}$
. Similarly,
$\lnot v_{i}\wedge \lnot \lnot v_{i}$
. Similarly,
![]() $t(v_{1},\ldots ,v_{k})$
may be put in conjunctive normal form
$t(v_{1},\ldots ,v_{k})$
may be put in conjunctive normal form
![]() $\bigwedge \nolimits _{s}D_{s}$
with
$\bigwedge \nolimits _{s}D_{s}$
with
![]() $D_{s}=e\vee \bigvee \nolimits _{r}\lnot ^{n_{r}}v_{i_{r}}$
and no occurrence of both
$D_{s}=e\vee \bigvee \nolimits _{r}\lnot ^{n_{r}}v_{i_{r}}$
and no occurrence of both
![]() $v_{i},\lnot \lnot v_{i}$
. We prove now a result on elimination of quantifiers. Let
$v_{i},\lnot \lnot v_{i}$
. We prove now a result on elimination of quantifiers. Let
![]() $Ext(\ell )$
denote the conjunction of the extension axioms
$Ext(\ell )$
denote the conjunction of the extension axioms
![]() $Ext_{\boldsymbol {A}}(k,f)$
for
$Ext_{\boldsymbol {A}}(k,f)$
for
![]() $k\leq \ell ,$
and define for formulas
$k\leq \ell ,$
and define for formulas
![]() $\varphi ,\psi \in \mathcal {L}_{\tau }^{\boldsymbol {A}^{+}}$
:
$\varphi ,\psi \in \mathcal {L}_{\tau }^{\boldsymbol {A}^{+}}$
:
![]() $\varphi \equiv _{Ext(\ell )}\psi $
iff
$\varphi \equiv _{Ext(\ell )}\psi $
iff
![]() $||\varphi (m_{1},\ldots ,m_{k})||^{\mathfrak {M}}=||\psi (m_{1},\ldots ,m_{k})||^{\mathfrak {M}}$
for any model
$||\varphi (m_{1},\ldots ,m_{k})||^{\mathfrak {M}}=||\psi (m_{1},\ldots ,m_{k})||^{\mathfrak {M}}$
for any model
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() $\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}}$
satisfying
$\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}}$
satisfying
![]() $Ext(\ell )$
, and any
$Ext(\ell )$
, and any
![]() $m_{1},\ldots ,m_{k}\in M$
.
$m_{1},\ldots ,m_{k}\in M$
.
Claim. Any formula
![]() $\varphi \in (\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}})^{(\ell )}$
is
$\varphi \in (\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}})^{(\ell )}$
is
![]() $Ext(\ell )$
-equivalent to a quantifier-free formula in the same free variables as
$Ext(\ell )$
-equivalent to a quantifier-free formula in the same free variables as
![]() $\varphi $
.
$\varphi $
.
We proceed by induction on the complexity of
![]() $\varphi $
. Assume by induction hypothesis that
$\varphi $
. Assume by induction hypothesis that
![]() $\varphi (x_{1},\ldots ,x_{k},x_{k+1})\equiv _{Ext(\ell )}\psi (x_{1},\ldots ,x_{k},x_{k+1})$
quantifier-free, and
$\varphi (x_{1},\ldots ,x_{k},x_{k+1})\equiv _{Ext(\ell )}\psi (x_{1},\ldots ,x_{k},x_{k+1})$
quantifier-free, and
![]() $k+1\leq \ell ,$
we must show the same for
$k+1\leq \ell ,$
we must show the same for
![]() $\exists x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
and
$\exists x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
and
![]() $\forall x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
. By the previous algebraic remarks, we may assume
$\forall x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
. By the previous algebraic remarks, we may assume
![]() $\psi $
is in disjunctive normal form, i.e.,
$\psi $
is in disjunctive normal form, i.e.,
![]() $\bigvee \nolimits _{s}C_{s}(x_{1},\ldots ,x_{k},x_{k+1})$
where each
$\bigvee \nolimits _{s}C_{s}(x_{1},\ldots ,x_{k},x_{k+1})$
where each
![]() $C_{s}$
is a conjunction:
$C_{s}$
is a conjunction:
![]() $C_{s}^{\prime }(x_{1},\ldots ,x_{k})$
being the part not containing the variable
$C_{s}^{\prime }(x_{1},\ldots ,x_{k})$
being the part not containing the variable
![]() $x_{k+1}$
, such that each atomic
$x_{k+1}$
, such that each atomic
![]() $R_{r}(x_{1},\ldots ,x_{k},x_{k+1})$
appearing in
$R_{r}(x_{1},\ldots ,x_{k},x_{k+1})$
appearing in
![]() $C_{s}$
does it in one and only one of the following forms:
$C_{s}$
does it in one and only one of the following forms:
Substitute the first three types of formulas with (the symbol)
![]() $1$
, the fourth with
$1$
, the fourth with
![]() $\varepsilon ,$
and the fifth with
$\varepsilon ,$
and the fifth with
![]() $\varepsilon ^{\prime }; $
and let c be the minimum of e and the substituted constants to obtain:
$\varepsilon ^{\prime }; $
and let c be the minimum of e and the substituted constants to obtain:
Since we have substituted the highest possible values in each case, we have for any model
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $x_{1},\ldots ,x_{k},i\in M$
:
$x_{1},\ldots ,x_{k},i\in M$
:
On the other hand, if
![]() $\mathfrak {M}$
satisfies
$\mathfrak {M}$
satisfies
![]() $Ext(\ell )$
and
$Ext(\ell )$
and
![]() $k+1\leq \ell ,$
there is, for any
$k+1\leq \ell ,$
there is, for any
![]() $x_{1},\ldots ,x_{k}$
in M, an
$x_{1},\ldots ,x_{k}$
in M, an
![]() $i_{0}\in M$
such that for each
$i_{0}\in M$
such that for each
![]() $R_{r}$
appearing in
$R_{r}$
appearing in
![]() $C_{s}(x_{1},\ldots ,x_{k},x_{k+1}),$
the atomic formula
$C_{s}(x_{1},\ldots ,x_{k},x_{k+1}),$
the atomic formula
![]() $R_{r}(x_{1},\ldots ,x_{k},i_{0})$
takes a value making the configuration in which it appears to take the highest possible value; that is,
$R_{r}(x_{1},\ldots ,x_{k},i_{0})$
takes a value making the configuration in which it appears to take the highest possible value; that is,
Therefore, for any
![]() $x_{1},\ldots ,x_{k}\in M$
$x_{1},\ldots ,x_{k}\in M$
 $$ \begin{align*} ||\exists x_{k+1}\,C_{s}(x_{1},\ldots,x_{k},x_{k+1})||^{\mathfrak{M}}&=\sup_{i\in M}||C_{s}(x_{1},\ldots,x_{k},i)||^{\mathfrak{M}}\\ &=||C_{s}^{+}(x_{1},\ldots,x_{k})||^{\mathfrak{M}} \end{align*} $$
$$ \begin{align*} ||\exists x_{k+1}\,C_{s}(x_{1},\ldots,x_{k},x_{k+1})||^{\mathfrak{M}}&=\sup_{i\in M}||C_{s}(x_{1},\ldots,x_{k},i)||^{\mathfrak{M}}\\ &=||C_{s}^{+}(x_{1},\ldots,x_{k})||^{\mathfrak{M}} \end{align*} $$
and, finally,
 $$ \begin{align*} ||\exists x_{k+1}\,\varphi (x_{1},\ldots,x_{k},x_{k+1})||^{\mathfrak{M}}&=||\bigvee\nolimits_{s}\exists x_{k+1}\,C_{s}(x_{1},\ldots,x_{k},i)||^{\mathfrak{M}}\\ &=||\bigvee\nolimits_{s}C_{s}^{+}(x_{1},\ldots,x_{k})||^{\mathfrak{M}}, \end{align*} $$
$$ \begin{align*} ||\exists x_{k+1}\,\varphi (x_{1},\ldots,x_{k},x_{k+1})||^{\mathfrak{M}}&=||\bigvee\nolimits_{s}\exists x_{k+1}\,C_{s}(x_{1},\ldots,x_{k},i)||^{\mathfrak{M}}\\ &=||\bigvee\nolimits_{s}C_{s}^{+}(x_{1},\ldots,x_{k})||^{\mathfrak{M}}, \end{align*} $$
showing that
![]() $\exists x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})\equiv _{Ext(\ell )}\bigvee \nolimits _{s}C_{s}^{+}(x_{1},\ldots ,x_{k})$
.
$\exists x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})\equiv _{Ext(\ell )}\bigvee \nolimits _{s}C_{s}^{+}(x_{1},\ldots ,x_{k})$
.
Symmetrically, one eliminates the quantifier in
![]() $\forall x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
using a conjunctive normal form of
$\forall x_{k+1}\,\varphi (x_{1},\ldots ,x_{k},x_{k+1})$
using a conjunctive normal form of
![]() $\psi $
and substituting in the elementary disjunction each configuration by its lowest possible value:
$\psi $
and substituting in the elementary disjunction each configuration by its lowest possible value:
 $$ \begin{align*} &R_{r} \text{ alone}, \lnot R_{r} \text{ alone}, \lnot \lnot R_{r} \text{ alone go to } 0,\\ &R_{r}\vee \lnot R_{r} \text{ goes to } \delta,\\ &\lnot R_{r}\vee \lnot \lnot R_{r} \text{ goes to } \delta ^{\prime }. \end{align*} $$
$$ \begin{align*} &R_{r} \text{ alone}, \lnot R_{r} \text{ alone}, \lnot \lnot R_{r} \text{ alone go to } 0,\\ &R_{r}\vee \lnot R_{r} \text{ goes to } \delta,\\ &\lnot R_{r}\vee \lnot \lnot R_{r} \text{ goes to } \delta ^{\prime }. \end{align*} $$
Finally, any sentence
![]() $\varphi \in (\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}})^{(\ell )}$
is
$\varphi \in (\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}})^{(\ell )}$
is
![]() $Ext(\ell )$
-equivalent to a quantifier-free sentence
$Ext(\ell )$
-equivalent to a quantifier-free sentence
![]() $\psi $
in
$\psi $
in
![]() $\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}},$
necessarily a
$\mathcal {L}_{\tau }^{\boldsymbol {A}^{+}},$
necessarily a
![]() $\wedge ,\vee ,\lnot $
combination of elements of E and thus an element e of E. Hence,
$\wedge ,\vee ,\lnot $
combination of elements of E and thus an element e of E. Hence,
![]() $\lim _n \mu _{n}(\varphi =e)\geq \lim _n \mu _{n}(Ext(\ell ))= 1$
.
$\lim _n \mu _{n}(\varphi =e)\geq \lim _n \mu _{n}(Ext(\ell ))= 1$
.
Clearly, the conditions of the theorem are satisfied by De Morgan algebras, which include Boolean algebras and the
![]() $\{\wedge ,\vee ,\lnot \}$
-reducts of
$\{\wedge ,\vee ,\lnot \}$
-reducts of
![]() $\mathrm {MV}$
-algebras. They are satisfied also by the
$\mathrm {MV}$
-algebras. They are satisfied also by the
![]() $\{\wedge ,\vee ,\lnot \}$
-reduct of any G-algebra since the law
$\{\wedge ,\vee ,\lnot \}$
-reduct of any G-algebra since the law
![]() $\lnot (v\wedge w)=\lnot v\vee \lnot w$
fails in arbitrary Heyting algebras but holds in prelinear ones.
$\lnot (v\wedge w)=\lnot v\vee \lnot w$
fails in arbitrary Heyting algebras but holds in prelinear ones.
Example 19. The almost sure values for any finite Boolean algebra are just
![]() $0$
and
$0$
and
![]() $1$
, since
$1$
, since
![]() $\varepsilon =\varepsilon ^{\prime }=0$
and
$\varepsilon =\varepsilon ^{\prime }=0$
and
![]() $\delta =\delta ^{\prime }=1$
.
$\delta =\delta ^{\prime }=1$
.
Example 20. The almost sure values for the
![]() $\{\wedge ,\vee ,\lnot \}$
-fragment of
$\{\wedge ,\vee ,\lnot \}$
-fragment of
![]() $\mathcal {L}^{{\mathrm {L}} _{N+1}}$
are
$\mathcal {L}^{{\mathrm {L}} _{N+1}}$
are
![]() $\{0,\frac {1}{2},1\}$
for even N, and
$\{0,\frac {1}{2},1\}$
for even N, and
![]() $\{0,\frac {N-1}{2N},\frac {N+1}{2N},1\}$
for odd N. Indeed,
$\{0,\frac {N-1}{2N},\frac {N+1}{2N},1\}$
for odd N. Indeed,
![]() $\varepsilon =\varepsilon ^{\prime }=\delta =\delta ^{\prime }=\frac {N/2}{N}$
in the first case, and
$\varepsilon =\varepsilon ^{\prime }=\delta =\delta ^{\prime }=\frac {N/2}{N}$
in the first case, and
![]() $\varepsilon =\varepsilon ^{\prime }=\max (v\wedge (1-v))=\frac {(N-1)/2}{N}$
,
$\varepsilon =\varepsilon ^{\prime }=\max (v\wedge (1-v))=\frac {(N-1)/2}{N}$
,
![]() $\delta =\delta ^{\prime }=\min (v\vee (1-v))=\frac {(N+1)/2}{N}$
in the second.
$\delta =\delta ^{\prime }=\min (v\vee (1-v))=\frac {(N+1)/2}{N}$
in the second.
Example 21. For any finite
![]() $\mathrm {G}$
-algebra
$\mathrm {G}$
-algebra
![]() $\boldsymbol {G}$
, the almost sure values of the
$\boldsymbol {G}$
, the almost sure values of the
![]() $\{\wedge ,\vee ,\lnot \}$
-fragment of
$\{\wedge ,\vee ,\lnot \}$
-fragment of
![]() $\mathcal {L}^{\boldsymbol {G}}$
are
$\mathcal {L}^{\boldsymbol {G}}$
are
![]() $0,\delta ,1,$
where
$0,\delta ,1,$
where
![]() $\delta =\inf (v\vee \lnot v)$
, since
$\delta =\inf (v\vee \lnot v)$
, since
![]() $\varepsilon =\varepsilon ^{\prime }=0$
and
$\varepsilon =\varepsilon ^{\prime }=0$
and
![]() $\delta ^{\prime }=\inf (\lnot v\vee \lnot \lnot v) = 0$
. Notice that
$\delta ^{\prime }=\inf (\lnot v\vee \lnot \lnot v) = 0$
. Notice that
![]() $\delta $
is the minimum dense element of
$\delta $
is the minimum dense element of
![]() $\boldsymbol {G}$
and the smallest positive element if
$\boldsymbol {G}$
and the smallest positive element if
![]() $\boldsymbol {G}$
is a chain.
$\boldsymbol {G}$
is a chain.
Example 22. The almost sure values for a finite De Morgan algebra are at most four since
![]() $\varepsilon =\varepsilon ^{\prime }$
and
$\varepsilon =\varepsilon ^{\prime }$
and
![]() $\delta =\delta ^{\prime }$
. Examples 19 and 20 show they may be exactly two, exactly three or exactly four.
$\delta =\delta ^{\prime }$
. Examples 19 and 20 show they may be exactly two, exactly three or exactly four.
Example 23. As the conditions of the theorem are equational, they are preserved by finite products; in particular, the reader may verify that the logic associated with the algebra ![]() has 5 distinct almost sure values:
has 5 distinct almost sure values:
![]() $0,\varepsilon =\varepsilon ^{\prime },\delta ,\delta ^{\prime },1$
. We let the reader find an example where six distinct values are achieved.
$0,\varepsilon =\varepsilon ^{\prime },\delta ,\delta ^{\prime },1$
. We let the reader find an example where six distinct values are achieved.
Notice that no new almost sure values are added by
![]() $(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(\omega )}$
because any sentence of this logic is asymptotically equivalent to a finitary one, as we prove next using our translation. Let
$(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(\omega )}$
because any sentence of this logic is asymptotically equivalent to a finitary one, as we prove next using our translation. Let
![]() $(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
denote the formulas in
$(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
denote the formulas in
![]() $(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(\omega )}$
utilizing at most the variables
$(\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(\omega )}$
utilizing at most the variables
![]() $\mathbf {x}=x_{1},\ldots ,x_{k}$
, free or bound. Define
$\mathbf {x}=x_{1},\ldots ,x_{k}$
, free or bound. Define
![]() $(\mathcal {L}^{\boldsymbol {A}})^{(k)}$
similarly, and denote by
$(\mathcal {L}^{\boldsymbol {A}})^{(k)}$
similarly, and denote by
![]() $\theta _{k}$
the conjunction of the classical extension axioms
$\theta _{k}$
the conjunction of the classical extension axioms
![]() $Ext_A(i,f)$
for
$Ext_A(i,f)$
for
![]() $i\leq k$
.
$i\leq k$
.
Lemma 24. Given a finite lattice algebra
![]() $\boldsymbol {A}$
, for any formula
$\boldsymbol {A}$
, for any formula
![]() $\varphi \in (\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
, there is a formula
$\varphi \in (\mathcal {L}^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
, there is a formula
![]() $\varphi ^{\prime }\in (\mathcal {L}^{\boldsymbol {A}})^{(k)}$
such that
$\varphi ^{\prime }\in (\mathcal {L}^{\boldsymbol {A}})^{(k)}$
such that
![]() $\theta _{k}\models \forall \mathbf {x}[\varphi ^{a}\leftrightarrow \varphi ^{\prime }{}^{a}]$
for any
$\theta _{k}\models \forall \mathbf {x}[\varphi ^{a}\leftrightarrow \varphi ^{\prime }{}^{a}]$
for any
![]() $a\in A$
. Hence,
$a\in A$
. Hence,
![]() $||\varphi ||^{\mathfrak {M}}=||\varphi ^{\prime }||^{\mathfrak {M}}$
in almost all finite models.
$||\varphi ||^{\mathfrak {M}}=||\varphi ^{\prime }||^{\mathfrak {M}}$
in almost all finite models.
Proof. We do it by induction on the complexity of
![]() $\varphi $
. We prove the inductive step for infinite conjunctions; the other inductive steps are similar or trivial. Assume
$\varphi $
. We prove the inductive step for infinite conjunctions; the other inductive steps are similar or trivial. Assume
![]() $\varphi _{n}\in (\mathcal {L}_{\tau }^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
,
$\varphi _{n}\in (\mathcal {L}_{\tau }^{\boldsymbol {A}})_{\omega _{1}\omega }^{(k)}$
,
![]() $\tau $
finite, and
$\tau $
finite, and
![]() $\theta _{k}\models \forall \mathbf {x}[\varphi _{n}^{a}\leftrightarrow \varphi _{n}^{\prime }{}^{a}]$
with
$\theta _{k}\models \forall \mathbf {x}[\varphi _{n}^{a}\leftrightarrow \varphi _{n}^{\prime }{}^{a}]$
with
![]() $\varphi _{n}^{\prime }\in (\mathcal {L}_{\tau }^{\boldsymbol {A}})^{(k)}$
for each
$\varphi _{n}^{\prime }\in (\mathcal {L}_{\tau }^{\boldsymbol {A}})^{(k)}$
for each
![]() $a\in A$
and
$a\in A$
and
![]() $n\in \omega $
. Then the classical random
$n\in \omega $
. Then the classical random
![]() $\tau $
-model
$\tau $
-model
![]() $\mathfrak {R}_{\tau \times A}$
(cf. Theorem 5) satisfies for each
$\mathfrak {R}_{\tau \times A}$
(cf. Theorem 5) satisfies for each
![]() $a\in A$
:
$a\in A$
:
 $$ \begin{align*} (\bigwedge_{n\in \omega}\varphi_{n})^{a}\leftrightarrow \lbrack \underset{b1\wedge \ldots\wedge b_{k}=a,k\leq |A|,n_{1},\ldots, n_{k}\in \omega }{\bigvee}\varphi_{n_{1}}^{\prime}{}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{\prime}{}^{b_{k}}]\wedge \bigwedge_{b\geq a}\bigvee\nolimits_{n\in \omega }\varphi_{n}^{\prime}{}^{b}. \end{align*} $$
$$ \begin{align*} (\bigwedge_{n\in \omega}\varphi_{n})^{a}\leftrightarrow \lbrack \underset{b1\wedge \ldots\wedge b_{k}=a,k\leq |A|,n_{1},\ldots, n_{k}\in \omega }{\bigvee}\varphi_{n_{1}}^{\prime}{}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{\prime}{}^{b_{k}}]\wedge \bigwedge_{b\geq a}\bigvee\nolimits_{n\in \omega }\varphi_{n}^{\prime}{}^{b}. \end{align*} $$
As
![]() $Th(R)$
is
$Th(R)$
is
![]() $\omega $
-categorical, by the Ryll–Nardzewski theorem, there is a finite subset
$\omega $
-categorical, by the Ryll–Nardzewski theorem, there is a finite subset
![]() $S\subseteq \omega $
such that any formula
$S\subseteq \omega $
such that any formula
![]() $\varphi _{n}^{\prime }(\mathbf {x})^{b}$
(with
$\varphi _{n}^{\prime }(\mathbf {x})^{b}$
(with
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $b\in A$
) is equivalent to one in the set
$b\in A$
) is equivalent to one in the set
![]() $\{\varphi _{n}^{\prime }(\mathbf {x})^{b}:n\in S, b\in A\}$
. Thus,
$\{\varphi _{n}^{\prime }(\mathbf {x})^{b}:n\in S, b\in A\}$
. Thus,
![]() $(\bigwedge _{n\in \omega }\varphi _{n})^{a}$
is equivalent in
$(\bigwedge _{n\in \omega }\varphi _{n})^{a}$
is equivalent in
![]() $\mathfrak {R}_{\tau \times A}$
to
$\mathfrak {R}_{\tau \times A}$
to
 $$ \begin{align*} \lbrack \underset{b1\wedge \ldots\wedge b_{k}, k\leq |A|,n_{1},\ldots, n_{k}\in S}{\bigvee}\varphi _{n_{1}}^{\prime}{}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{\prime}{}^{b_{k}}]\wedge \bigwedge_{b\geq a}\bigvee_{n\in S}\varphi _{n}^{\prime}{}^{b}, \end{align*} $$
$$ \begin{align*} \lbrack \underset{b1\wedge \ldots\wedge b_{k}, k\leq |A|,n_{1},\ldots, n_{k}\in S}{\bigvee}\varphi _{n_{1}}^{\prime}{}^{b_{1}}\wedge \ldots\wedge \varphi_{n_{k}}^{\prime}{}^{b_{k}}]\wedge \bigwedge_{b\geq a}\bigvee_{n\in S}\varphi _{n}^{\prime}{}^{b}, \end{align*} $$
clearly equivalent to
![]() $(\bigwedge _{n\in S}\varphi _{n}^{\prime })^{a}$
. Then
$(\bigwedge _{n\in S}\varphi _{n}^{\prime })^{a}$
. Then
![]() $\theta _{k}\models \forall \mathbf {x}[(\bigwedge _{n\in \omega }\varphi _{n})^{a}\leftrightarrow (\bigwedge _{n\in S}\varphi _{n})^{a}]$
; otherwise, by [Reference Ebbinghaus and Flum15, Claim (4), in Section 4.2], we obtain
$\theta _{k}\models \forall \mathbf {x}[(\bigwedge _{n\in \omega }\varphi _{n})^{a}\leftrightarrow (\bigwedge _{n\in S}\varphi _{n})^{a}]$
; otherwise, by [Reference Ebbinghaus and Flum15, Claim (4), in Section 4.2], we obtain
![]() $\theta _{k}\models \lnot \forall \mathbf {x}[(\bigwedge _{n\in \omega }\varphi _{n})^{a}\leftrightarrow (\bigwedge _{n\in S}\varphi _{n})^{a}]$
, contradicting that the equivalence holds in
$\theta _{k}\models \lnot \forall \mathbf {x}[(\bigwedge _{n\in \omega }\varphi _{n})^{a}\leftrightarrow (\bigwedge _{n\in S}\varphi _{n})^{a}]$
, contradicting that the equivalence holds in
![]() $\mathfrak {R}_{\tau \times A}$
.
$\mathfrak {R}_{\tau \times A}$
.
5. A zero-one law for infinitely valued Łukasiewicz predicate logic
Proving zero-one laws for logics given by infinite lattice algebras seems challenging. The translation yields in this case infinitary formulas with essentially infinite vocabularies, and it is known that in the case of vocabularies with an infinite supply of unary predicate symbols, the zero-one law for classical
![]() $\mathcal {L}_{\omega _{1}\omega }^{\omega }$
fails [Reference Ebbinghaus and Flum15, Exercise 4.1.9.]. Moreover, we cannot expect positive probabilities
$\mathcal {L}_{\omega _{1}\omega }^{\omega }$
fails [Reference Ebbinghaus and Flum15, Exercise 4.1.9.]. Moreover, we cannot expect positive probabilities
![]() $p_{R}(a)$
for all the truth-values (except for countable A).
$p_{R}(a)$
for all the truth-values (except for countable A).
We will deal mainly with infinitely valued Łukasiewicz logic, determined by the standard
![]() $\mathrm {MV}$
-algebra
$\mathrm {MV}$
-algebra
![]() $[0,1]_{\mathrm {L}}={\langle {[0,1],\wedge ,\vee ,\rightarrow ,\lnot }\rangle }$
with crip identity (cf. [Reference Hájek26]).
$[0,1]_{\mathrm {L}}={\langle {[0,1],\wedge ,\vee ,\rightarrow ,\lnot }\rangle }$
with crip identity (cf. [Reference Hájek26]).
Consider
![]() $\sigma $
-additive Borel probability measures
$\sigma $
-additive Borel probability measures
![]() $\{p_{R}\}_{R\in \tau }$
over
$\{p_{R}\}_{R\in \tau }$
over
![]() $[0,1]$
which assign positive measure to all non-trivial intervals of
$[0,1]$
which assign positive measure to all non-trivial intervals of
![]() $[0,1]$
, say,
$[0,1]$
, say,
![]() $p_{R}=$
Lebesgue measure. These induce a product measure
$p_{R}=$
Lebesgue measure. These induce a product measure
![]() $\rho _{n}$
in the infinite space of models with domain
$\rho _{n}$
in the infinite space of models with domain
![]() $[n]$
:
$[n]$
:
![]() $\mathrm {Mod}_{\tau ,n}^{[0,1]}=\prod _{R\in \tau }[0,1]^{[n]^{\tau (R)}}\!$
, which permits to define for any measurable set
$\mathrm {Mod}_{\tau ,n}^{[0,1]}=\prod _{R\in \tau }[0,1]^{[n]^{\tau (R)}}\!$
, which permits to define for any measurable set
![]() $S \subseteq [0,1]$
the probability that a sentence
$S \subseteq [0,1]$
the probability that a sentence
![]() $\varphi $
takes a value in
$\varphi $
takes a value in
![]() $S:$
$S:$
(the map
![]() $\mathfrak {M}\longmapsto \varphi ^{\mathfrak {M}}$
is measurable because it may be shown to be continuous).
$\mathfrak {M}\longmapsto \varphi ^{\mathfrak {M}}$
is measurable because it may be shown to be continuous).
It is important to stress that for each pair of predicates R and
![]() $R^{\prime }$
, and
$R^{\prime }$
, and
![]() $i_{1},\ldots ,i_{k},i_{1}^{\prime },\ldots ,i_{k}^{\prime }\in [ n]$
, we have that
$i_{1},\ldots ,i_{k},i_{1}^{\prime },\ldots ,i_{k}^{\prime }\in [ n]$
, we have that
![]() $R(i_{1},\ldots ,i_{k}) \in S$
and
$R(i_{1},\ldots ,i_{k}) \in S$
and
![]() $R^{\prime }(i_{1}^{\prime },\ldots ,i_{k}^{\prime }) \in S'$
become independent events provided that the tuples
$R^{\prime }(i_{1}^{\prime },\ldots ,i_{k}^{\prime }) \in S'$
become independent events provided that the tuples
![]() ${\langle {R,i_{1},\ldots ,i_{k}}\rangle }$
and
${\langle {R,i_{1},\ldots ,i_{k}}\rangle }$
and
![]() ${\langle {R^{\prime },i_{1}^{\prime },\ldots ,i_{k}^{\prime }}\rangle }$
are distinct.
${\langle {R^{\prime },i_{1}^{\prime },\ldots ,i_{k}^{\prime }}\rangle }$
are distinct.
For simplicity, we will use the notation
![]() $\mathfrak {M}\models \varphi $
as an equivalent of
$\mathfrak {M}\models \varphi $
as an equivalent of
![]() $||\varphi ||^{\mathfrak {M}} = 1$
.
$||\varphi ||^{\mathfrak {M}} = 1$
.
Theorem 25. For any sentence
![]() $\varphi \in \mathcal {L }^{[0,1]_{\mathrm {L}}}$
, there is a unique
$\varphi \in \mathcal {L }^{[0,1]_{\mathrm {L}}}$
, there is a unique
![]() $a\in [ 0,1]$
such that
$a\in [ 0,1]$
such that
Equivalently,
The two formulations are clearly equivalent. They say that
![]() $\varphi $
takes approximately value a with probability
$\varphi $
takes approximately value a with probability
![]() $1$
, for any degree of approximation. To prove the theorem, we will need the following observations on the expressivity of the logic (see [Reference Belluce7, Reference Chang13, Reference Mundici34]). For each fraction
$1$
, for any degree of approximation. To prove the theorem, we will need the following observations on the expressivity of the logic (see [Reference Belluce7, Reference Chang13, Reference Mundici34]). For each fraction
![]() $r=\frac {n}{m} \in [0,1]$
, there are connectives of Łukasiewicz logic
$r=\frac {n}{m} \in [0,1]$
, there are connectives of Łukasiewicz logic
![]() $( )_{\geq r}$
,
$( )_{\geq r}$
,
![]() $( )_{\leq r}$
such that
$( )_{\leq r}$
such that
 $$ \begin{align*} \mathfrak{M} &\models \varphi _{\geq r} \text{ iff } ||\varphi||^{\mathfrak{M}}\geq r,\\ \mathfrak{M} &\models \varphi _{\geq r} \text{ iff } ||\varphi||^{\mathfrak{M}}\leq r. \end{align*} $$
$$ \begin{align*} \mathfrak{M} &\models \varphi _{\geq r} \text{ iff } ||\varphi||^{\mathfrak{M}}\geq r,\\ \mathfrak{M} &\models \varphi _{\geq r} \text{ iff } ||\varphi||^{\mathfrak{M}}\leq r. \end{align*} $$
More generally and precisely (see [Reference Caicedo and Iovino8]),
 $$ \begin{align*} &||\varphi_{\geq r}||^{\mathfrak{M}}\geq 1-\varepsilon \text{ iff } ||\varphi||^{\mathfrak{M}}\geq r-\frac{\varepsilon }{m}\\ &||\varphi_{\leq r}||^{\mathfrak{M}}\geq 1-\varepsilon \text{ iff } ||\varphi||^{\mathfrak{M}}\leq r+\frac{\varepsilon }{m} \end{align*} $$
$$ \begin{align*} &||\varphi_{\geq r}||^{\mathfrak{M}}\geq 1-\varepsilon \text{ iff } ||\varphi||^{\mathfrak{M}}\geq r-\frac{\varepsilon }{m}\\ &||\varphi_{\leq r}||^{\mathfrak{M}}\geq 1-\varepsilon \text{ iff } ||\varphi||^{\mathfrak{M}}\leq r+\frac{\varepsilon }{m} \end{align*} $$
We will assume also that the logic
![]() $\mathcal {L}^{[0,1]_{\mathrm {L}}}$
has a ‘crisp identity’
$\mathcal {L}^{[0,1]_{\mathrm {L}}}$
has a ‘crisp identity’
![]() $\approx $
taking only the values
$\approx $
taking only the values
![]() $0$
or
$0$
or
![]() $1$
.Footnote
3
$1$
.Footnote
3
Given
![]() $k,N\in \omega ,$
let
$k,N\in \omega ,$
let
![]() $F_{k+1}$
consist of all the atomic formulas distinct from identities truly containing the variable
$F_{k+1}$
consist of all the atomic formulas distinct from identities truly containing the variable
![]() $x_{k+1},$
and
$x_{k+1},$
and
![]() $A_{N}=\{[\frac {j}{N},\frac {j+1}{N}]$
,
$A_{N}=\{[\frac {j}{N},\frac {j+1}{N}]$
,
![]() $j=0,\ldots , N-1\}$
. For each choice of intervals
$j=0,\ldots , N-1\}$
. For each choice of intervals
![]() $g \colon F_{k+1}\longrightarrow A_{N}$
, define the extension axiom
$g \colon F_{k+1}\longrightarrow A_{N}$
, define the extension axiom
![]() $Ext_{A}(k,N,g)$
:
$Ext_{A}(k,N,g)$
:
 $$ \begin{align*} \forall x_{1}\ldots x_{k}\,(\bigvee\nolimits_{i\not=j}x_{i}&\approx x_{j}\vee \exists x_{k+1}\,\bigwedge\nolimits_{i\leq k}\lnot x_{k+1}\\&\approx x_{j}\wedge \bigwedge\nolimits_{\varphi \in F_{k+1}}\varphi _{g(\varphi)}(x_{1},\ldots, x_{k},x_{k+1})) \end{align*} $$
$$ \begin{align*} \forall x_{1}\ldots x_{k}\,(\bigvee\nolimits_{i\not=j}x_{i}&\approx x_{j}\vee \exists x_{k+1}\,\bigwedge\nolimits_{i\leq k}\lnot x_{k+1}\\&\approx x_{j}\wedge \bigwedge\nolimits_{\varphi \in F_{k+1}}\varphi _{g(\varphi)}(x_{1},\ldots, x_{k},x_{k+1})) \end{align*} $$
Then define the sentence
![]() $Ext_{A}(k,N)$
:
$Ext_{A}(k,N)$
:
and the theory
Due to the semantical interpretation of quantifiers as infima and suprema, we have that
![]() $Ext_{A}(k,N,g)^{M}\geq 1-\varepsilon $
if and only if for any distinct
$Ext_{A}(k,N,g)^{M}\geq 1-\varepsilon $
if and only if for any distinct
![]() $i_{1},\ldots ,i_{k}$
in M there is an i in
$i_{1},\ldots ,i_{k}$
in M there is an i in
![]() $M\setminus \{i_{1},\ldots ,i_{k}\}$
such that
$M\setminus \{i_{1},\ldots ,i_{k}\}$
such that
![]() $||\varphi _{g(\varphi )}||^{\mathfrak {M}}(i_{1},\ldots ,i_{k},i)\geq 1-\varepsilon $
for each
$||\varphi _{g(\varphi )}||^{\mathfrak {M}}(i_{1},\ldots ,i_{k},i)\geq 1-\varepsilon $
for each
![]() $\varphi \in F_{k+1}$
. More precisely, if
$\varphi \in F_{k+1}$
. More precisely, if
![]() $g(\varphi )=[\frac {j}{N},\frac {j+1}{N}],$
$g(\varphi )=[\frac {j}{N},\frac {j+1}{N}],$
 $$ \begin{align*} ||\varphi ||^{\mathfrak{M}}(i_{1},\ldots ,i_{k},i)\in \left[ \frac{j}{N}-\frac{\varepsilon }{m},\frac{j+1}{N}+\frac{\varepsilon }{m}\right], \end{align*} $$
$$ \begin{align*} ||\varphi ||^{\mathfrak{M}}(i_{1},\ldots ,i_{k},i)\in \left[ \frac{j}{N}-\frac{\varepsilon }{m},\frac{j+1}{N}+\frac{\varepsilon }{m}\right], \end{align*} $$
for each
![]() $\varphi \in F_{k+1}$
, which is a relaxation of the intended condition
$\varphi \in F_{k+1}$
, which is a relaxation of the intended condition
 $$ \begin{align*}||\varphi ||^{\mathfrak{M}}(i_{1},\ldots ,i_{k},i_{k+1})\in \left[ \frac{j}{N},\frac{j+1}{N}\right].\end{align*} $$
$$ \begin{align*}||\varphi ||^{\mathfrak{M}}(i_{1},\ldots ,i_{k},i_{k+1})\in \left[ \frac{j}{N},\frac{j+1}{N}\right].\end{align*} $$
In the following, we will denote by
![]() $g(\varphi )_{\pm \varepsilon }$
the displayed relaxed interval.
$g(\varphi )_{\pm \varepsilon }$
the displayed relaxed interval.
Lemma 26. For any
![]() $\varepsilon>0$
, the sequence
$\varepsilon>0$
, the sequence
![]() $\mu _{n}(Ext_{A}(k,N,g)\geq 1-\varepsilon )$
converges to
$\mu _{n}(Ext_{A}(k,N,g)\geq 1-\varepsilon )$
converges to
![]() $1$
.
$1$
.
Proof. Fix to natural numbers k and N, a mapping
![]() $g \colon F_{k+1}\longrightarrow A_{N}$
and recall that according to the previous observation
$g \colon F_{k+1}\longrightarrow A_{N}$
and recall that according to the previous observation
![]() $Ext_{A}(k,g,N)^{M}<1-\varepsilon $
means that there are distinct
$Ext_{A}(k,g,N)^{M}<1-\varepsilon $
means that there are distinct
![]() $i_{1},\ldots ,i_{k}$
in
$i_{1},\ldots ,i_{k}$
in
![]() $[n]$
such that:
$[n]$
such that:
for all
![]() $i\in [ n]\setminus \{i_{1},\ldots ,i_{k}\}$
, it is false that
$i\in [ n]\setminus \{i_{1},\ldots ,i_{k}\}$
, it is false that
![]() $\bigwedge \nolimits _{\varphi \in F_{k+1}}||\varphi ||^{\mathfrak {M}}(i_{1},\ldots ,i_{k},i)\in g(\varphi )_{\pm \varepsilon }$
.
$\bigwedge \nolimits _{\varphi \in F_{k+1}}||\varphi ||^{\mathfrak {M}}(i_{1},\ldots ,i_{k},i)\in g(\varphi )_{\pm \varepsilon }$
.
Let
![]() $S(M,\varepsilon ,i_{1},\ldots ,i_{k})$
be the above classical statement for fixed
$S(M,\varepsilon ,i_{1},\ldots ,i_{k})$
be the above classical statement for fixed
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $i_{1},\ldots ,i_{k}$
, and
$i_{1},\ldots ,i_{k}$
, and
![]() $\mathfrak {M}$
chosen randomly in
$\mathfrak {M}$
chosen randomly in
![]() $\mathrm {Mod}_{\tau ,n}^{[0,1]}$
. Then, since the set of events
$\mathrm {Mod}_{\tau ,n}^{[0,1]}$
. Then, since the set of events
is independent,
But
![]() $\mu _n (\varphi (i_{1},\ldots ,i_{k},i)\in g(\varphi )_{\pm \varepsilon })=p_{R}(g(\varphi )_{\pm \varepsilon })\geq p_{R}([\frac {j}{N},\frac {j+1}{N}])>0,$
for some relation symbol R and some j. Then, taking
$\mu _n (\varphi (i_{1},\ldots ,i_{k},i)\in g(\varphi )_{\pm \varepsilon })=p_{R}(g(\varphi )_{\pm \varepsilon })\geq p_{R}([\frac {j}{N},\frac {j+1}{N}])>0,$
for some relation symbol R and some j. Then, taking
![]() $\delta _{N}=\min \{p_{R}([\frac {j}{N},\frac {j+1}{N}]):R\in \tau $
,
$\delta _{N}=\min \{p_{R}([\frac {j}{N},\frac {j+1}{N}]):R\in \tau $
,
![]() $0\leq j\leq N-1\},$
we have
$0\leq j\leq N-1\},$
we have
Therefore,
which clearly converges to
![]() $0,$
since
$0,$
since
![]() $1-\delta _{N}<1$
. Therefore,
$1-\delta _{N}<1$
. Therefore,
![]() $\mu _{n}(Ext_{A}(k,g,N)\geq 1-\varepsilon )$
converges to
$\mu _{n}(Ext_{A}(k,g,N)\geq 1-\varepsilon )$
converges to
![]() $1$
.
$1$
.
Recall that
![]() $Ext_{A}(k,N,g)^{\mathfrak {M}}\geq 1-\varepsilon $
iff
$Ext_{A}(k,N,g)^{\mathfrak {M}}\geq 1-\varepsilon $
iff
![]() $M\models Ext_{A}(k,N,g)_{\geq 1-\varepsilon }$
. Therefore, the previous lemma shows that any finite subset of the theory
$M\models Ext_{A}(k,N,g)_{\geq 1-\varepsilon }$
. Therefore, the previous lemma shows that any finite subset of the theory
![]() $Ext^{\ast }=\{\psi _{\geq 1-\varepsilon }:\psi \in Ext$
,
$Ext^{\ast }=\{\psi _{\geq 1-\varepsilon }:\psi \in Ext$
,
![]() $\varepsilon>0)$
is satisfiable. Hence, by satisfiability compactness of Łukasiewicz logic it has a model, which will be necessarily a model of
$\varepsilon>0)$
is satisfiable. Hence, by satisfiability compactness of Łukasiewicz logic it has a model, which will be necessarily a model of
![]() $Ext$
. As
$Ext$
. As
![]() $Ext$
is countable, this model may be chosen to be countable by the downward Löwenheim–Skolem theorem.
$Ext$
is countable, this model may be chosen to be countable by the downward Löwenheim–Skolem theorem.
Definition 1. Let
![]() $\overline {a},\overline {b}$
be tuples of the same length k of distinct elements of
$\overline {a},\overline {b}$
be tuples of the same length k of distinct elements of
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B},$
respectively, then
$\mathfrak {B},$
respectively, then
![]() $\overline {a}\sim _{\varepsilon }\overline {b}$
if and only if
$\overline {a}\sim _{\varepsilon }\overline {b}$
if and only if
![]() $|\varphi ^{\mathfrak {A}}(\overline {a})-\varphi ^{\mathfrak {B}}(\overline {b})|\leq \varepsilon $
for any atomic
$|\varphi ^{\mathfrak {A}}(\overline {a})-\varphi ^{\mathfrak {B}}(\overline {b})|\leq \varepsilon $
for any atomic
![]() $\varphi $
with variables in
$\varphi $
with variables in
![]() $\{x_{1},\ldots ,x_{k}\}$
. We say then that the pair
$\{x_{1},\ldots ,x_{k}\}$
. We say then that the pair
![]() $\overline {a},\overline {b}$
(or the assignment
$\overline {a},\overline {b}$
(or the assignment
![]() $a_{i}\mapsto b_{i})$
is an
$a_{i}\mapsto b_{i})$
is an
![]() $\varepsilon $
-partial isomorphism.
$\varepsilon $
-partial isomorphism.
Considering tuples enumerating
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
respectively, we may define, similarly, the notion of
$\mathfrak {B}$
respectively, we may define, similarly, the notion of
![]() $\varepsilon $
-isomorphism. Partial
$\varepsilon $
-isomorphism. Partial
![]() $\varepsilon $
-isomorphisms between models of
$\varepsilon $
-isomorphisms between models of
![]() $Ext$
have the extension property, more precisely.
$Ext$
have the extension property, more precisely.
Lemma 27. If
![]() $\mathfrak {A},\mathfrak {B}\models Ext(k,N)$
,
$\mathfrak {A},\mathfrak {B}\models Ext(k,N)$
,
![]() $N\geq \frac {2}{\varepsilon }$
, then
$N\geq \frac {2}{\varepsilon }$
, then
![]() $\overline {a}\sim _{\varepsilon }\overline {b}$
(of length
$\overline {a}\sim _{\varepsilon }\overline {b}$
(of length
![]() $\leq k)$
implies for any
$\leq k)$
implies for any
![]() $a\in A\setminus \{\overline {a}\}$
there is
$a\in A\setminus \{\overline {a}\}$
there is
![]() $b\in B\setminus \{\overline {b}\}$
such that
$b\in B\setminus \{\overline {b}\}$
such that
![]() $\overline {a}a\sim _{\varepsilon }\overline {bb}$
and viceversa. Particular case: for any
$\overline {a}a\sim _{\varepsilon }\overline {bb}$
and viceversa. Particular case: for any
![]() $a\in A$
, there is
$a\in A$
, there is
![]() $b\in B$
such that
$b\in B$
such that
![]() $a\sim _{\varepsilon } b$
.
$a\sim _{\varepsilon } b$
.
Proof. Assume
![]() $\overline {a}\sim _{\varepsilon }\overline {b},$
and consider
$\overline {a}\sim _{\varepsilon }\overline {b},$
and consider
![]() $g \colon F_{k+1}\longrightarrow A_{N}$
such that
$g \colon F_{k+1}\longrightarrow A_{N}$
such that
![]() $\varphi ^{\mathfrak {A}}(\overline {a},a)\in g(\varphi )$
for each
$\varphi ^{\mathfrak {A}}(\overline {a},a)\in g(\varphi )$
for each
![]() $\varphi \in F_{k+1}$
, then
$\varphi \in F_{k+1}$
, then
![]() $Ext(k,N,g)$
is an extension axiom which must be satisfied by
$Ext(k,N,g)$
is an extension axiom which must be satisfied by
![]() $\mathfrak {B};$
hence, there is b such that
$\mathfrak {B};$
hence, there is b such that
![]() $||\varphi _{g(\varphi )}||^{\mathfrak {B}}(\overline {b},b)\geq 1-\varepsilon /2$
. From this, we obtain that
$||\varphi _{g(\varphi )}||^{\mathfrak {B}}(\overline {b},b)\geq 1-\varepsilon /2$
. From this, we obtain that
![]() $\varphi ^{\mathfrak {B}}(\overline {b},b)\in [ \frac {j}{N}-\varepsilon /2,\frac {j+1}{N}+\varepsilon /2],$
thus
$\varphi ^{\mathfrak {B}}(\overline {b},b)\in [ \frac {j}{N}-\varepsilon /2,\frac {j+1}{N}+\varepsilon /2],$
thus
![]() $|\varphi ^{\mathfrak {A}}(\overline {a},a)-\varphi ^{\mathfrak {B}}(\overline {b},b)|\leq \frac {1}{N}+\frac {\varepsilon }{2}\leq \varepsilon |.$
$|\varphi ^{\mathfrak {A}}(\overline {a},a)-\varphi ^{\mathfrak {B}}(\overline {b},b)|\leq \frac {1}{N}+\frac {\varepsilon }{2}\leq \varepsilon |.$
We will utilize the following observation:
![]() $|(r\oplus s)-(r^{\prime }\oplus s^{\prime })|\leq 2\max \{|r-r^{\prime }|,|s-s^{\prime }|\}$
. For any formula #
$|(r\oplus s)-(r^{\prime }\oplus s^{\prime })|\leq 2\max \{|r-r^{\prime }|,|s-s^{\prime }|\}$
. For any formula #
![]() $\varphi$
, let
$\varphi$
, let
![]() $(\varphi )$
be the number of occurrences of
$(\varphi )$
be the number of occurrences of
![]() $\oplus $
in
$\oplus $
in
![]() $\varphi $
.
$\varphi $
.
Lemma 28. If
![]() $\mathfrak {A},\mathfrak {B}\models Ext(k,N)$
,
$\mathfrak {A},\mathfrak {B}\models Ext(k,N)$
,
![]() $N\geq \frac {2}{\varepsilon },$
then for any formula
$N\geq \frac {2}{\varepsilon },$
then for any formula
![]() $\varphi $
with free variables in
$\varphi $
with free variables in
![]() $\{x_{1},\ldots ,x_{k}\}$
,
$\{x_{1},\ldots ,x_{k}\}$
,
![]() $\overline {a}\sim _{\varepsilon }\overline {b}$
implies
$\overline {a}\sim _{\varepsilon }\overline {b}$
implies
![]() $|\varphi ^{\mathfrak {A}}(\overline {a})-\varphi ^{\mathfrak {B}}(\overline {b})|\leq 2^{\#(\varphi )}\varepsilon $
.
$|\varphi ^{\mathfrak {A}}(\overline {a})-\varphi ^{\mathfrak {B}}(\overline {b})|\leq 2^{\#(\varphi )}\varepsilon $
.
Proof. By induction on the complexity of ![]() based in
based in
![]() $\oplus $
,
$\oplus $
,
![]() $\lnot $
,
$\lnot $
,
![]() $\exists $
.
$\exists $
.
-
• If
 $\varphi $
is atomic, then the result is immediate by definition of partial
$\varphi $
is atomic, then the result is immediate by definition of partial
 $\varepsilon $
-isomorphism.
$\varepsilon $
-isomorphism. -
• If
 $\varphi $
is
$\varphi $
is
 $\lnot \theta $
, then it is trivial because
$\lnot \theta $
, then it is trivial because
 $|(\lnot \theta )^{\mathfrak {A}}[\overline {a}]-(\lnot \theta )^{\mathfrak {B}}[\overline {b}]|=|\theta ^{\mathfrak {A}}[\overline {a}]-\theta ^{\mathfrak {B}}[\overline {b}]|.$
$|(\lnot \theta )^{\mathfrak {A}}[\overline {a}]-(\lnot \theta )^{\mathfrak {B}}[\overline {b}]|=|\theta ^{\mathfrak {A}}[\overline {a}]-\theta ^{\mathfrak {B}}[\overline {b}]|.$
-
• If
 $\varphi $
is
$\varphi $
is
 $\theta \oplus \theta ^{\prime }$
, then, by induction hypothesis,
$\theta \oplus \theta ^{\prime }$
, then, by induction hypothesis,
 $|\theta ^{\mathfrak {A}}[\overline {a}]-\theta ^{\mathfrak {B}}[\overline {b}]|\leq 2^{\#(\theta )}\varepsilon $
,
$|\theta ^{\mathfrak {A}}[\overline {a}]-\theta ^{\mathfrak {B}}[\overline {b}]|\leq 2^{\#(\theta )}\varepsilon $
,
 $|\theta ^{\prime \mathfrak {A}}[\overline {a}]- \theta ^{\prime \mathfrak {B}}[\overline {b}]|\leq 2^{\#(\theta ^{\prime })}\varepsilon $
and
$|\theta ^{\prime \mathfrak {A}}[\overline {a}]- \theta ^{\prime \mathfrak {B}}[\overline {b}]|\leq 2^{\#(\theta ^{\prime })}\varepsilon $
and
 $|(\theta \oplus \theta ^{\prime })^{\mathfrak {A}}[\overline {a}]-(\theta \oplus \theta ^{\prime })^{\mathfrak {B}}[\overline {b}]|\leq 2\cdot 2^{\max (\#(\theta ),\#(\theta ^{\prime }))}\varepsilon \leq 2^{\#(\theta )+\#(\theta ^{\prime })+1}\varepsilon =2^{\#(\varphi )}\varepsilon .$
$|(\theta \oplus \theta ^{\prime })^{\mathfrak {A}}[\overline {a}]-(\theta \oplus \theta ^{\prime })^{\mathfrak {B}}[\overline {b}]|\leq 2\cdot 2^{\max (\#(\theta ),\#(\theta ^{\prime }))}\varepsilon \leq 2^{\#(\theta )+\#(\theta ^{\prime })+1}\varepsilon =2^{\#(\varphi )}\varepsilon .$
-
• If
 $\varphi $
is
$\varphi $
is
 $\exists v\,\theta $
and
$\exists v\,\theta $
and
 $\overline {a}\sim _{\varepsilon }\overline {b}$
, then, by the previous lemma, for each
$\overline {a}\sim _{\varepsilon }\overline {b}$
, then, by the previous lemma, for each
 $a\in A$
there is
$a\in A$
there is
 $b_{a}\in B$
such that
$b_{a}\in B$
such that
 $\overline {a}a\sim _{\varepsilon }\overline {b}b_{a},$
and the inductive hypothesis yields
$\overline {a}a\sim _{\varepsilon }\overline {b}b_{a},$
and the inductive hypothesis yields
 $|\theta ^{\mathfrak {A}}[\overline {a}a]-\theta ^{\mathfrak {B}}[\overline {b}b_{a}]|\leq 2^{\#(\theta )}\varepsilon .$
Hence,
$|\theta ^{\mathfrak {A}}[\overline {a}a]-\theta ^{\mathfrak {B}}[\overline {b}b_{a}]|\leq 2^{\#(\theta )}\varepsilon .$
Hence,
 $\theta ^{\mathfrak {A}}[\overline {a}a]\leq \theta ^{\mathfrak {B}}[\overline {b}b_{a}]+2^{\#(\theta )}\varepsilon $
. Taking suprema over a, we obtain
$\theta ^{\mathfrak {A}}[\overline {a}a]\leq \theta ^{\mathfrak {B}}[\overline {b}b_{a}]+2^{\#(\theta )}\varepsilon $
. Taking suprema over a, we obtain
 $(\exists v\,\theta )^{\mathfrak {A}}[\overline {a}]\leq \sup _{b_{a}}\theta ^{\mathfrak {B}}[\overline {b}b_{a}]+2^{\#(\theta )}\varepsilon \leq (\exists v\,\theta )^{\mathfrak {B}}+2^{\#(\theta )}\varepsilon [\overline {b}],$
and thus
$(\exists v\,\theta )^{\mathfrak {A}}[\overline {a}]\leq \sup _{b_{a}}\theta ^{\mathfrak {B}}[\overline {b}b_{a}]+2^{\#(\theta )}\varepsilon \leq (\exists v\,\theta )^{\mathfrak {B}}+2^{\#(\theta )}\varepsilon [\overline {b}],$
and thus
 $(\exists v\,\theta )^{\mathfrak {A}}[\overline {a}]-(\exists v\,\theta )^{\mathfrak {B}}[\overline {b}]\leq 2^{\#(\theta )}\varepsilon .$
Symmetrically, we get the same for the negation and thus
$(\exists v\,\theta )^{\mathfrak {A}}[\overline {a}]-(\exists v\,\theta )^{\mathfrak {B}}[\overline {b}]\leq 2^{\#(\theta )}\varepsilon .$
Symmetrically, we get the same for the negation and thus
 $|(\exists v\,\theta )^{\mathfrak {A}}[\overline {b}]-(\exists v\theta )^{B}[\overline {a}]|\leq 2^{\#(\theta )}\varepsilon =2^{\#(\varphi )}\varepsilon $
.
$|(\exists v\,\theta )^{\mathfrak {A}}[\overline {b}]-(\exists v\theta )^{B}[\overline {a}]|\leq 2^{\#(\theta )}\varepsilon =2^{\#(\varphi )}\varepsilon $
.
We will write
![]() $\mathfrak {A}\equiv _{\mathcal {L }^{[0,1]_{\mathrm {L}}}}\mathfrak {B}$
whenever
$\mathfrak {A}\equiv _{\mathcal {L }^{[0,1]_{\mathrm {L}}}}\mathfrak {B}$
whenever
![]() $\varphi ^{\mathfrak {A}}=\varphi ^{\mathfrak {B}}$
for each sentence
$\varphi ^{\mathfrak {A}}=\varphi ^{\mathfrak {B}}$
for each sentence
![]() $\varphi $
.
$\varphi $
.
Corollary 29 (Completeness).
If
![]() $\mathfrak {A},\mathfrak {B}\models Ext$
, then
$\mathfrak {A},\mathfrak {B}\models Ext$
, then
![]() $\mathfrak {A}\equiv _{\mathcal {L}^{[0,1]_{\mathrm {L}}}}\mathfrak {B}$
. Therefore,
$\mathfrak {A}\equiv _{\mathcal {L}^{[0,1]_{\mathrm {L}}}}\mathfrak {B}$
. Therefore,
![]() $Ext$
is complete.
$Ext$
is complete.
Proof. Given a sentence
![]() $\varphi $
and
$\varphi $
and
![]() $\varepsilon>0,$
let
$\varepsilon>0,$
let
![]() $x_{1},\ldots ,x_{k}$
be its variables and
$x_{1},\ldots ,x_{k}$
be its variables and
![]() $N\geq 2\cdot 2^{\#(\varphi )}/\varepsilon $
. Then, by Lemma 27, there are
$N\geq 2\cdot 2^{\#(\varphi )}/\varepsilon $
. Then, by Lemma 27, there are
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
such that
$b\in B$
such that
![]() $a\sim _{\varepsilon /2^{\#(\varphi )}}b$
and, by Lemma 28,
$a\sim _{\varepsilon /2^{\#(\varphi )}}b$
and, by Lemma 28,
![]() $|\varphi ^{\mathfrak {A}}-\varphi ^{\mathfrak {B}}|=|\varphi ^{\mathfrak {A}}[a]-\varphi ^{\mathfrak {B}}[b]|\leq 2^{\#(\varphi )}\varepsilon /2^{\#(\varphi )}=\varepsilon $
. Since this is true for all
$|\varphi ^{\mathfrak {A}}-\varphi ^{\mathfrak {B}}|=|\varphi ^{\mathfrak {A}}[a]-\varphi ^{\mathfrak {B}}[b]|\leq 2^{\#(\varphi )}\varepsilon /2^{\#(\varphi )}=\varepsilon $
. Since this is true for all
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $\varphi ^{\mathfrak {A}}=\varphi ^{\mathfrak {B}}$
.
$\varphi ^{\mathfrak {A}}=\varphi ^{\mathfrak {B}}$
.
It is easy to see that a theory T is complete iff for any sentence
![]() $\varphi $
and rational r, we have
$\varphi $
and rational r, we have
![]() $T\models \varphi _{\geq r}$
or
$T\models \varphi _{\geq r}$
or
![]() $T\models \varphi _{\leq r}.$
$T\models \varphi _{\leq r}.$
Proof of Theorem 25.
Fix a sentence
![]() $\varphi $
. By completeness, one has
$\varphi $
. By completeness, one has
![]() $Ext\models \varphi _{\geq r}$
or
$Ext\models \varphi _{\geq r}$
or
![]() $Ext\models \varphi _{\leq r}\,$
for each rational
$Ext\models \varphi _{\leq r}\,$
for each rational
![]() $r\in [ 0,1]$
. Then, the sets
$r\in [ 0,1]$
. Then, the sets
![]() $L=\{r\in \mathbb {Q}:Ext\models \varphi _{\geq r}\}$
,
$L=\{r\in \mathbb {Q}:Ext\models \varphi _{\geq r}\}$
,
![]() $U=\{s\in \mathbb {Q}:Ext\models \varphi _{\leq s}\}$
are easily seen to determine a real cut
$U=\{s\in \mathbb {Q}:Ext\models \varphi _{\leq s}\}$
are easily seen to determine a real cut
![]() $a\in [ 0,1]$
. Assume first that
$a\in [ 0,1]$
. Assume first that
![]() $a\in (0,1)$
and let
$a\in (0,1)$
and let
![]() $a\in (r,s)$
and
$a\in (r,s)$
and
![]() $r<r^{\prime }<a<s^{\prime }<s$
. Then,
$r<r^{\prime }<a<s^{\prime }<s$
. Then,
![]() $Ext\models \varphi _{\geq r^{\prime }}\wedge \varphi _{\leq s^{\prime }}$
by construction. Take a positive
$Ext\models \varphi _{\geq r^{\prime }}\wedge \varphi _{\leq s^{\prime }}$
by construction. Take a positive
![]() $\varepsilon <s-s^{\prime },rs^{\prime }-r$
. By the approximate consequence compactness of Ł, there is a subset
$\varepsilon <s-s^{\prime },rs^{\prime }-r$
. By the approximate consequence compactness of Ł, there is a subset
![]() $Ext^{\ast }\subseteq _{fin}Ext$
such that
$Ext^{\ast }\subseteq _{fin}Ext$
such that
![]() $Ext^{\ast }\models (\varphi _{\geq r^{\prime }}\wedge \varphi _{\leq s^{\prime }})_{\geq 1-\varepsilon }$
, thus
$Ext^{\ast }\models (\varphi _{\geq r^{\prime }}\wedge \varphi _{\leq s^{\prime }})_{\geq 1-\varepsilon }$
, thus
![]() $Ext^{\ast }\models \varphi _{[ r^{\prime }-\varepsilon ,\text { }s^{\prime }+\varepsilon ]}$
. From the fact that
$Ext^{\ast }\models \varphi _{[ r^{\prime }-\varepsilon ,\text { }s^{\prime }+\varepsilon ]}$
. From the fact that
![]() $\lim _n \mu _{n}(Ext^{\ast })= 1$
, we obtain
$\lim _n \mu _{n}(Ext^{\ast })= 1$
, we obtain
![]() $\lim _n \mu _{n}(\varphi \in [ r^{\prime }-\varepsilon ,s^{\prime }+\varepsilon ])= 1$
and, a fortiori,
$\lim _n \mu _{n}(\varphi \in [ r^{\prime }-\varepsilon ,s^{\prime }+\varepsilon ])= 1$
and, a fortiori,
![]() $\lim _n\mu _{n}(\varphi \in (r,s))= 1$
. This shows the existence of a. Uniqueness follows easily since
$\lim _n\mu _{n}(\varphi \in (r,s))= 1$
. This shows the existence of a. Uniqueness follows easily since
![]() $b\not =a$
implies the existence of rationals
$b\not =a$
implies the existence of rationals
![]() $u,v$
, r such that
$u,v$
, r such that
![]() $u<b<r<a<s.$
As
$u<b<r<a<s.$
As
![]() $\varphi \in (r,s)$
has asymptotic probability
$\varphi \in (r,s)$
has asymptotic probability
![]() $1$
, the incompatible event
$1$
, the incompatible event
![]() $\varphi \in (u,r)$
must have asymptotic probability
$\varphi \in (u,r)$
must have asymptotic probability
![]() $0$
.
$0$
.
If
![]() $a\in [ 0,s)$
, choose
$a\in [ 0,s)$
, choose
![]() $a<s^{\prime }<s$
. Then,
$a<s^{\prime }<s$
. Then,
![]() $Ext\models \varphi _{\leq s^{\prime }}$
and
$Ext\models \varphi _{\leq s^{\prime }}$
and
![]() $Ext^{\ast }\models (\varphi _{\leq s^{\prime }})_{1-\varepsilon }$
for an
$Ext^{\ast }\models (\varphi _{\leq s^{\prime }})_{1-\varepsilon }$
for an
![]() $\varepsilon <s-s^{\prime }$
, and hence
$\varepsilon <s-s^{\prime }$
, and hence
![]() $Ext^{\ast }\models \varphi _{[ 0,s^{\prime }+\varepsilon ]}$
. Since
$Ext^{\ast }\models \varphi _{[ 0,s^{\prime }+\varepsilon ]}$
. Since
![]() $\lim _n\mu _{n}(Ext^{\ast })= 1$
, we have
$\lim _n\mu _{n}(Ext^{\ast })= 1$
, we have
![]() $\lim _n\mu _{n}(\varphi \in [ 0,s^{\prime }+\varepsilon ])= 1$
, and, a fortiori,
$\lim _n\mu _{n}(\varphi \in [ 0,s^{\prime }+\varepsilon ])= 1$
, and, a fortiori,
![]() $\lim _n \mu _{n}(\varphi \in [ 0,s))= 1$
. The case
$\lim _n \mu _{n}(\varphi \in [ 0,s))= 1$
. The case
![]() $a=1$
is similar.
$a=1$
is similar.
Remark 30. The inductive step in Lemma 28 works without extra effort for any continuous connective
![]() $\circ $
under the rank definition:
$\circ $
under the rank definition:
![]() $\#(\circ (\theta _{1},\ldots $
,
$\#(\circ (\theta _{1},\ldots $
,
![]() $\theta _{k}))=\max _{i}\#(\theta _{i})+1$
. So
$\theta _{k}))=\max _{i}\#(\theta _{i})+1$
. So
![]() $Ext$
is complete for any expansion of Łukasiewicz logic by continuous connectives, and thus for full continuous logic with crisp identity, and the same is true of the zero-one law.
$Ext$
is complete for any expansion of Łukasiewicz logic by continuous connectives, and thus for full continuous logic with crisp identity, and the same is true of the zero-one law.
Remark 31. From lemmas 27 and 28, one may show that, for any countable
![]() $\mathfrak {A},\mathfrak {B}\models Ext$
and
$\mathfrak {A},\mathfrak {B}\models Ext$
and
![]() $\varepsilon>0$
, there are enumerations
$\varepsilon>0$
, there are enumerations
![]() $a_{0},a_{1},\ldots $
of A and
$a_{0},a_{1},\ldots $
of A and
![]() $b_{0},b_{1},\ldots $
of B such that
$b_{0},b_{1},\ldots $
of B such that
![]() $a_{i}\mapsto b_{i}$
is an
$a_{i}\mapsto b_{i}$
is an
![]() $\varepsilon $
-isomorphism. These enumerations depend on
$\varepsilon $
-isomorphism. These enumerations depend on
![]() $\varepsilon $
and it is not possible to obtain
$\varepsilon $
and it is not possible to obtain
![]() $\omega $
-categoricity in this way. However, it follows from the above proof that any sentence
$\omega $
-categoricity in this way. However, it follows from the above proof that any sentence
![]() $\phi $
takes in all models of
$\phi $
takes in all models of
![]() $Ext$
the same value, precisely its almost sure truth-value.
$Ext$
the same value, precisely its almost sure truth-value.
6. Further results for infinitely valued predicate logics
Although we cannot expect a complete description of the infinitely valued case, in this section we still obtain some results generalizing those in Section 4. In particular, we obtain that all rational numbers in
![]() $[0,1]$
are almost sure values of infinitely valued Łukasiewicz predicate logic, and we prove a zero-one law for a large family of logics satisfying De Morgan laws with values in closed sublattices of
$[0,1]$
are almost sure values of infinitely valued Łukasiewicz predicate logic, and we prove a zero-one law for a large family of logics satisfying De Morgan laws with values in closed sublattices of
![]() $[0,1]$
.
$[0,1]$
.
Observe that the analogue of Lemma 13 holds for infinitely valued Łukasiewicz logic with a similar proof, due to the continuity of McNaughton functions.
Theorem 32. Let
![]() $t(v_{1},\ldots ,v_{k})$
be a term in the signature of
$t(v_{1},\ldots ,v_{k})$
be a term in the signature of
![]() $\mathrm {MV}$
-algebras. Then, the values
$\mathrm {MV}$
-algebras. Then, the values
![]() $m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
$m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
![]() $s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure for
$s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure for
![]() $\boldsymbol {A}=[0,1]_{\mathrm {L}}$
.
$\boldsymbol {A}=[0,1]_{\mathrm {L}}$
.
Proof. Notice first that m and s exist by compactness of
![]() $[0,1]$
and the continuity of
$[0,1]$
and the continuity of
![]() $t^{\boldsymbol {A}}$
. Let
$t^{\boldsymbol {A}}$
. Let
![]() $R(x)$
be an atomic formula in one variable. We show that for any open interval V of
$R(x)$
be an atomic formula in one variable. We show that for any open interval V of
![]() $[0,1]$
containing m:
$[0,1]$
containing m:
By definition of m, there is a tuple
![]() ${\langle {a_{j}}\rangle }_{j}\in |A|^{k}$
such that
${\langle {a_{j}}\rangle }_{j}\in |A|^{k}$
such that
![]() $t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})\in V$
and by continuity of
$t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})\in V$
and by continuity of
![]() $t^{\boldsymbol {A}}$
, there are open intervals
$t^{\boldsymbol {A}}$
, there are open intervals
![]() $V_{j}$
such that
$V_{j}$
such that
![]() $a_{j}\in V_{j}$
and
$a_{j}\in V_{j}$
and
![]() $v_{j}\in V_{j}$
implies
$v_{j}\in V_{j}$
implies
![]() $t^{\boldsymbol {A}}(v_{1},\ldots ,v_{k})\in V.$
$t^{\boldsymbol {A}}(v_{1},\ldots ,v_{k})\in V.$
For each
![]() $n\geq k$
, find
$n\geq k$
, find
![]() $K\subseteq [ n]^{k}$
of cardinal
$K\subseteq [ n]^{k}$
of cardinal
![]() $|K|=\lfloor n/k\rfloor $
such that all tuples in K have all their components distinct, and two different tuples in K are distinct at each coordinate. Then,
$|K|=\lfloor n/k\rfloor $
such that all tuples in K have all their components distinct, and two different tuples in K are distinct at each coordinate. Then,
 $$ \begin{align*} &\quad \mu _{n}(\forall x_{1}\ldots\forall x_{k}\,(t(R(x_{1}),\ldots,R(x_{k}))\in V)\\ &\quad =\Pr (\inf\limits_{i_{1},\ldots,i_{k}\in [n]}t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))\in V)\\ &\quad =\Pr (\text{for some } (i_{j})_{j} \text{ in } [n]^{k}:t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))\in V) (\text{since } V \text{ is an open}\\ &\qquad\quad\text{interval containing } m)\\ &\quad \geq \Pr (\text{for some } (i_{j})_{j} \text{ in } [n]^{k}:R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k).\\ &\quad \geq \Pr (\text{for some } (i_{j})_{j} \text{ in } K:R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k)\\ &\quad =1-\Pr (\text{for all } (i_{j})_{j} \text{ in } K \text{ is false: } R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k)\\ &\quad =1-\prod\nolimits_{(i_{1}\ldots i_{k})\in K}[1-\Pr (R(i_{j})\in V_{j} \text{ for } j=1,\ldots,k)]\\ &\quad =1-(1-p_{R}(V_{1})\ldots p_{R}(V_{k}))^{\lfloor n/k\rfloor}. \end{align*} $$
$$ \begin{align*} &\quad \mu _{n}(\forall x_{1}\ldots\forall x_{k}\,(t(R(x_{1}),\ldots,R(x_{k}))\in V)\\ &\quad =\Pr (\inf\limits_{i_{1},\ldots,i_{k}\in [n]}t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))\in V)\\ &\quad =\Pr (\text{for some } (i_{j})_{j} \text{ in } [n]^{k}:t^{\boldsymbol{A}}(R(i_{1}),\ldots,R(i_{k}))\in V) (\text{since } V \text{ is an open}\\ &\qquad\quad\text{interval containing } m)\\ &\quad \geq \Pr (\text{for some } (i_{j})_{j} \text{ in } [n]^{k}:R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k).\\ &\quad \geq \Pr (\text{for some } (i_{j})_{j} \text{ in } K:R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k)\\ &\quad =1-\Pr (\text{for all } (i_{j})_{j} \text{ in } K \text{ is false: } R(i_{j})\in V_{j}, \text{ for } j=1,\ldots,k)\\ &\quad =1-\prod\nolimits_{(i_{1}\ldots i_{k})\in K}[1-\Pr (R(i_{j})\in V_{j} \text{ for } j=1,\ldots,k)]\\ &\quad =1-(1-p_{R}(V_{1})\ldots p_{R}(V_{k}))^{\lfloor n/k\rfloor}. \end{align*} $$
For the last two identities, we use that the events
![]() $R(i_{j})\in V_{j}$
form a mutually independent set for the coordinates of the k-tupes in K. Since
$R(i_{j})\in V_{j}$
form a mutually independent set for the coordinates of the k-tupes in K. Since
![]() $p_{R}(V_{i})>0$
, the last quantity converges to
$p_{R}(V_{i})>0$
, the last quantity converges to
![]() $1$
when n goes to
$1$
when n goes to
![]() $\infty $
.
$\infty $
.
A similar argument shows that, for any open set V containing s,
converges to
![]() $1$
.
$1$
.
Corollary 33. All rational numbers are almost sure values of
![]() $[0,1]$
-valued Łukasiewicz logic (
$[0,1]$
-valued Łukasiewicz logic (
![]() $\mathcal {L}^{[0,1]_{\mathrm {L}}}$
).
$\mathcal {L}^{[0,1]_{\mathrm {L}}}$
).
Proof. Use the same terms of Example 15.
It is easy to see that Theorem 32 generalizes to any bounded linearly ordered lattice algebra for which the additional operations are continuous with respect to the order topology because its proof only uses the continuity of the functions interpreting the terms.
Theorem 34. Let
![]() $t(v_{1},\ldots ,v_{k})$
be a term for a bounded linearly ordered lattice algebra
$t(v_{1},\ldots ,v_{k})$
be a term for a bounded linearly ordered lattice algebra
![]() $\boldsymbol {A}$
. If
$\boldsymbol {A}$
. If
![]() $t^{\boldsymbol {A}}$
is continuous w.r.t. the order topology, then
$t^{\boldsymbol {A}}$
is continuous w.r.t. the order topology, then
![]() $m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
$m=\inf _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
and
![]() $s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure for
$s=\sup _{a_{1},\ldots ,a_{k}\in A}t^{\boldsymbol {A}}(a_{1},\ldots ,a_{k})$
are almost sure for
![]() $\mathcal {L}^{\boldsymbol {A}}$
whenever they exist.
$\mathcal {L}^{\boldsymbol {A}}$
whenever they exist.
Example 35. Consider Łukasiewicz logic with product. Then observe that
![]() $\frac {1}{2}(\sqrt {5}-1)=\inf (\lnot v\vee (v\cdot v))$
is an almost-sure value.
$\frac {1}{2}(\sqrt {5}-1)=\inf (\lnot v\vee (v\cdot v))$
is an almost-sure value.
Example 36. Let
![]() $\boldsymbol {G}_\uparrow $
be the G-chain consisting of an ascending sequence from
$\boldsymbol {G}_\uparrow $
be the G-chain consisting of an ascending sequence from
![]() $0$
to
$0$
to
![]() $1$
. Then, it may be checked that Gödel implication is continuous in this case. Therefore, all elements of
$1$
. Then, it may be checked that Gödel implication is continuous in this case. Therefore, all elements of
![]() $\boldsymbol {G}_\uparrow $
are almost sure (compare with Example 39 below).
$\boldsymbol {G}_\uparrow $
are almost sure (compare with Example 39 below).
Finally, notice that the analogue of Lemma 18 holds for infinite closed sublattices of
![]() $[0,1]$
with a continuous negation and actually gives a proof of the zero-one law in this case.
$[0,1]$
with a continuous negation and actually gives a proof of the zero-one law in this case.
Theorem 37. Let
![]() $\boldsymbol {A}={\langle {A,\wedge ,\vee ,\lnot }\rangle }$
be an infinite closed sublattice of
$\boldsymbol {A}={\langle {A,\wedge ,\vee ,\lnot }\rangle }$
be an infinite closed sublattice of
![]() $[0,1]$
containing
$[0,1]$
containing
![]() $0$
and
$0$
and
![]() $1$
with a continuous negation satisfying:
$1$
with a continuous negation satisfying:
-
(1)
 $\lnot (v\wedge w)=\lnot v\vee \lnot w$
,
$\lnot (v\wedge w)=\lnot v\vee \lnot w$
,
 $\lnot (v\vee w)=\lnot v\wedge \lnot w$
$\lnot (v\vee w)=\lnot v\wedge \lnot w$
-
(2)
 $v\leq \lnot \lnot v$
$v\leq \lnot \lnot v$
-
(3)
 $\lnot 1=0$
$\lnot 1=0$
Then,
![]() $\mathcal {L}^{\boldsymbol {A}}$
satisfies the zero-one law and its only almost sure values are
$\mathcal {L}^{\boldsymbol {A}}$
satisfies the zero-one law and its only almost sure values are
![]() $0$
,
$0$
,
![]() $1$
, and
$1$
, and
 $$ \begin{align*} &\varepsilon = \sup\limits_{x\in A}(x\wedge \lnot x), \varepsilon ^{\prime}=\sup\limits_{x\in A}(\lnot x\wedge \lnot \lnot x),\\ &\delta =\inf\limits_{x\in A}(x\vee \lnot x), \delta ^{\prime}=\inf\limits_{x\in A}(\lnot x\vee \lnot \lnot x). \end{align*} $$
$$ \begin{align*} &\varepsilon = \sup\limits_{x\in A}(x\wedge \lnot x), \varepsilon ^{\prime}=\sup\limits_{x\in A}(\lnot x\wedge \lnot \lnot x),\\ &\delta =\inf\limits_{x\in A}(x\vee \lnot x), \delta ^{\prime}=\inf\limits_{x\in A}(\lnot x\vee \lnot \lnot x). \end{align*} $$
Proof. This is essentially the same argument as in Theorem 18. By compactness of
![]() $\boldsymbol {A}$
and continuity of the operations, the displayed infima and suprema are attained, for example
$\boldsymbol {A}$
and continuity of the operations, the displayed infima and suprema are attained, for example
![]() $\varepsilon =(a\wedge \lnot a)$
for some
$\varepsilon =(a\wedge \lnot a)$
for some
![]() $a \in A$
, and they are almost sure by Theorem 34. Thus, only finitely many extension axioms are needed to ensure that the suprema of the various configurations R,
$a \in A$
, and they are almost sure by Theorem 34. Thus, only finitely many extension axioms are needed to ensure that the suprema of the various configurations R,
![]() $\lnot R$
,
$\lnot R$
,
![]() $\lnot \lnot R$
,
$\lnot \lnot R$
,
![]() $R\wedge \lnot R$
,
$R\wedge \lnot R$
,
![]() $\lnot R\wedge \lnot \lnot R$
appearing in the proof of Lemma 18 are realized (the same holds for the infima), and the quantifier elimination may be achieved with asymptotic probability
$\lnot R\wedge \lnot \lnot R$
appearing in the proof of Lemma 18 are realized (the same holds for the infima), and the quantifier elimination may be achieved with asymptotic probability
![]() $1$
.
$1$
.
Example 38. The logic given by the
![]() $\{\land , \lor , \neg \}$
-reduct of the Łukasiewicz algebra
$\{\land , \lor , \neg \}$
-reduct of the Łukasiewicz algebra
![]() $[0,1]_{\mathrm {L}}$
has almost sure values
$[0,1]_{\mathrm {L}}$
has almost sure values
![]() $\{0,\frac {1}{2},1\}.$
$\{0,\frac {1}{2},1\}.$
Example 39. The logic given by the
![]() $\{\wedge , \vee , \neg \}$
-reduct of any closed subalgebra of the standard
$\{\wedge , \vee , \neg \}$
-reduct of any closed subalgebra of the standard
![]() $\mathrm {G}$
-chain over
$\mathrm {G}$
-chain over
![]() $[0,1]$
in which
$[0,1]$
in which
![]() $0$
is isolated has a zero-one law, and its almost sure values are
$0$
is isolated has a zero-one law, and its almost sure values are
![]() $\{0,\delta ,1\}$
where
$\{0,\delta ,1\}$
where
![]() $\delta $
is the minimum positive element since
$\delta $
is the minimum positive element since
![]() $\wedge , \vee $
are continuous and, under isolation of
$\wedge , \vee $
are continuous and, under isolation of
![]() $0$
, Gödel negation becomes continuous.
$0$
, Gödel negation becomes continuous.
7. Final remarks
The translation we have used in the case of finite algebras has appeared in [Reference Badia, Caicedo and Noguera1, Reference Badia, Fagin and Noguera2] and permits to transfer straightforwardly from classical to finitely valued logics most relevant model-theoretic facts and concepts: compactness, ultraproducts, elementary embeddings, type omission, etc.
Grädel et al. [Reference Grädel, Helal, Naaf, Wilke, Baier and Fisman22] consider certain semirings
![]() $\boldsymbol {A}={\langle {A,+,\cdot ,0,1}\rangle }$
as algebras of truth values in which
$\boldsymbol {A}={\langle {A,+,\cdot ,0,1}\rangle }$
as algebras of truth values in which
![]() $\vee $
and
$\vee $
and
![]() $\wedge $
are interpreted as
$\wedge $
are interpreted as
![]() $+$
and
$+$
and
![]() $\cdot $
, and the quantifiers
$\cdot $
, and the quantifiers
![]() $\exists $
and
$\exists $
and
![]() $\forall $
are interpreted as iterated
$\forall $
are interpreted as iterated
![]() $+$
and
$+$
and
![]() $\cdot $
, respectively. Negation is allowed at the atomic level only, and no further operations (connectives) are allowed. In this setting, they obtain zero-one laws for finite distributive lattices and “absorptive” semirings such as
$\cdot $
, respectively. Negation is allowed at the atomic level only, and no further operations (connectives) are allowed. In this setting, they obtain zero-one laws for finite distributive lattices and “absorptive” semirings such as
![]() ${\langle {{\mathrm {L}}_{N+1},\vee ,\odot ,0,1}\rangle }$
. Our results in the present paper generalize those on lattice semirings because we do not require distributivity, and we allow arbitrary additional operations. Moreover, the treatment of negation in [Reference Grädel, Helal, Naaf, Wilke, Baier and Fisman22] can be expressed in terms of Oberschelp conditions.
${\langle {{\mathrm {L}}_{N+1},\vee ,\odot ,0,1}\rangle }$
. Our results in the present paper generalize those on lattice semirings because we do not require distributivity, and we allow arbitrary additional operations. Moreover, the treatment of negation in [Reference Grädel, Helal, Naaf, Wilke, Baier and Fisman22] can be expressed in terms of Oberschelp conditions.
Notice that the zero-one law fails for the simplest non-lattice semiring, namely the two-element field
![]() $\mathbb {F}_{2}={\langle {\{0,1\},+,\cdot ,0,1}\rangle }$
, as witnessed by the sentence
$\mathbb {F}_{2}={\langle {\{0,1\},+,\cdot ,0,1}\rangle }$
, as witnessed by the sentence
![]() $\exists x(Px\vee \lnot Px)$
whose value in universes of cardinal n is
$\exists x(Px\vee \lnot Px)$
whose value in universes of cardinal n is
![]() $\Sigma _{x\in [n]}1$
, which oscillates between
$\Sigma _{x\in [n]}1$
, which oscillates between
![]() $0$
and
$0$
and
![]() $1$
with the parity of n (negation is interpreted by the function
$1$
with the parity of n (negation is interpreted by the function
![]() $v+1$
so that
$v+1$
so that
![]() $Pi\vee \lnot Pi$
takes the value
$Pi\vee \lnot Pi$
takes the value
![]() $v+v+1 = 1$
for any
$v+v+1 = 1$
for any
![]() $i \in [n]$
, and
$i \in [n]$
, and
![]() $\exists $
is interpreted by
$\exists $
is interpreted by
![]() $\Sigma $
).
$\Sigma $
).
It is worth noting that, in the context of continuous model theory, a zero-one law is proved in [Reference Goldbring, Hart and Kruckman20] for the theory of metric spaces, which yields a zero-one law for Łukasiewicz of pure identity under certain restrictions.
We conclude with some questions that merit further investigation:
-
(1) Does
 $\mathcal {L}^{[0,1]_{\mathrm {L}}}$
have almost sure irrational values?
$\mathcal {L}^{[0,1]_{\mathrm {L}}}$
have almost sure irrational values? -
(2) Does full Łukasiewicz logic over
 $[0,1]$
with product and its (discontinuous) residuated implication have a zero-one law?
$[0,1]$
with product and its (discontinuous) residuated implication have a zero-one law? -
(3) Does full Gödel logic over
 $[0,1]$
have a zero-one law?
$[0,1]$
have a zero-one law? -
(4) The set
 $A_{as}$
of almost sure values of a logic
$A_{as}$
of almost sure values of a logic
 $\mathcal {L}^{\boldsymbol {A}}$
is an invariant of
$\mathcal {L}^{\boldsymbol {A}}$
is an invariant of
 $\boldsymbol {A}$
, in fact, a subalgebra. Is there a characterization of
$\boldsymbol {A}$
, in fact, a subalgebra. Is there a characterization of
 $A_{as}$
in purely algebraic terms?
$A_{as}$
in purely algebraic terms?
Acknowledgments
We are grateful to an anonymous reviewer for this journal who provided very useful remarks (including interesting historical insights) that helped improve substantially the quality of the article.
Funding statement
Badia was supported by the Australian Research Council grant DE220100544. Badia and Noguera were also supported by the European Union’s Marie Sklodowska–Curie grant no. 101007627 (MOSAIC project) and by GNSAGA, gruppo nazionale di ricerca INdAM.