An embedding of a metric graph 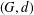$(G,d)$ on a closed hyperbolic surface is essential if each complementary region has a negative Euler characteristic. We show, by construction, that given any metric graph, its metric can be rescaled so that it admits an essential and isometric embedding on a closed hyperbolic surface. The essential genus $g_{e}(G)$ of $(G,d)$ is the lowest genus of a surface on which such an embedding is possible. We establish a formula to compute 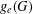$g_{e}(G)$ and show that, for every integer 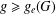$g\geq g_{e}(G)$, there is an embedding of 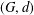$(G,d)$ (possibly after a rescaling of $d$) on a surface of genus 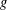$g$. Next, we study minimal embeddings where each complementary region has Euler characteristic $-1$. The maximum essential genus 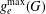$g_{e}^{\max }(G)$ of 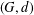$(G,d)$ is the largest genus of a surface on which the graph is minimally embedded. We describe a method for an essential embedding of 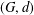$(G,d)$, where 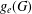$g_{e}(G)$ and 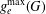$g_{e}^{\max }(G)$ are realised.

A filling of a closed hyperbolic surface is a set of simple closed geodesics whose complement is a disjoint union of hyperbolic polygons. The systolic length is the length of a shortest essential closed geodesic on the surface. A geodesic is called systolic, if the systolic length is realised by its length. For every $g\geq 2$, we construct closed hyperbolic surfaces of genus $g$ whose systolic geodesics fill the surfaces with complements consisting of only two components. Finally, we remark that one can deform the surfaces obtained to increase the systole.