In 1955, Lehto showed that, for every measurable function $\psi $ on the unit circle ${\mathbb T}$ , there is a function f holomorphic in the unit disc ${{\mathbb D}}$ , having $\psi $ as radial limit a.e. on ${\mathbb T}$ . We consider an analogous boundary value problem, where the unit disc is replaced by a Stein domain on a complex manifold and radial approach to a boundary point p is replaced by (asymptotically) total approach to p.

Let 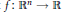$f\,:\,{{\mathbb{R}}^{n}}\,\to \,\mathbb{R}$ be 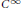${{C}^{\infty }}$ and let 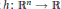$h\,:\,{{\mathbb{R}}^{n}}\,\to \,\mathbb{R}$ be positive and continuous. For any unbounded nondecreasing sequence 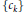$\{{{c}_{k}}\}$ of nonnegative real numbers and for any sequence without accumulation points $\{{{x}_{m}}\}$ in 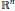${{\mathbb{R}}^{n}}$, there exists an entire function 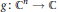$g\,:\,{{\mathbb{C}}^{n}}\,\to \,\mathbb{C}$ taking real values on 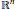${{\mathbb{R}}^{n}}$ such that

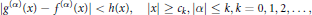$$\left| {{g}^{\left( \alpha \right)}}\left( x \right)-{{f}^{\left( \alpha \right)}}\left( x \right) \right|\text{ }<h\left( x \right),\left| x \right|\ge {{c}_{k}},\left| \alpha \right|\le k,k=0,1,2,...,$$

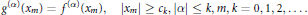$${{g}^{\left( \alpha \right)}}\left( {{x}_{m}} \right)\,=\,{{f}^{\left( \alpha \right)}}\left( {{x}_{m}} \right),\,\,\,\left| {{x}_{m}} \right|\,\ge \,{{c}_{k}},\,\left| \alpha \right|\,\le \,k,\,m,\,k\,=\,0,\,1,\,2,\,.\,.\,.\,.$$

This is a version for functions of several variables of the case $n\,=\,1$ due to $L$. Hoischen.