Let $n$ be an integer congruent to $0$ or $3$ modulo $4$. Under the assumption of the ABC conjecture, we prove that, given any integer $m$ fulfilling only a certain coprimeness condition, there exist infinitely many imaginary quadratic fields having an everywhere unramified Galois extension of group $A_n \times C_m$. The same result is obtained unconditionally in special cases.

In this article, we provide an explicit upper bound for $h_K \mathcal {R}_K d_K^{-1/2}$ which depends on an effective constant in the error term of the Ideal Theorem.

Let p be a prime with $p\equiv 1\pmod {4}$ . Gauss first proved that $2$ is a quartic residue modulo p if and only if $p=x^2+64y^2$ for some $x,y\in \Bbb Z$ and various expressions for the quartic residue symbol $(\frac {2}{p})_4$ are known. We give a new characterisation via a permutation, the sign of which is determined by $(\frac {2}{p})_4$ . The permutation is induced by the rule $x \mapsto y-x$ on the $(p-1)/4$ solutions $(x,y)$ to $x^2+y^2\equiv 0 \pmod {p}$ satisfying $1\leq x < y \leq (p-1)/2$ .

We construct a random model to study the distribution of class numbers in special families of real quadratic fields ${\open Q}(\sqrt d )$ arising from continued fractions. These families are obtained by considering continued fraction expansions of the form $\sqrt {D(n)} = [f(n),\overline {u_1,u_2, \ldots ,u_{s-1} ,2f(n)]} $ with fixed coefficients u1, …, us−1 and generalize well-known families such as Chowla's 4n2 + 1, for which analogous results were recently proved by Dahl and Lamzouri [‘The distribution of class numbers in a special family of real quadratic fields’, Trans. Amer. Math. Soc. (2018), 6331–6356].

We explicitly find regulators of an infinite family $\{{{L}_{m}}\}$ of the simplest quartic function fields with a parameter $m$ in a polynomial ring ${{\mathbb{F}}_{q}}\left( t \right)$, where ${{\mathbb{F}}_{q}}$ is the finite field of order $q$ with odd characteristic. In fact, this infinite family of the simplest quartic function fields are subfields of maximal real subfields of cyclotomic function fields having the same conductors. We obtain a lower bound on the class numbers of the family $\{{{L}_{m}}\}$ and some result on the divisibility of the divisor class numbers of cyclotomic function fields that contain $\{{{L}_{m}}\}$ as their subfields. Furthermore, we find an explicit criterion for the characterization of splitting types of all the primes of the rational function field ${{\mathbb{F}}_{q}}\left( t \right)$ in $\{{{L}_{m}}\}$.

We construct unconditionally several families of number fields with the largest possible class numbers. They are number fields of degree 4 and 5 whose Galois closures have the Galois group ${{A}_{4}},\,{{S}_{4}}$, and ${{S}_{5}}$. We first construct families of number fields with smallest regulators, and by using the strong Artin conjecture and applying the zero density result of Kowalski–Michel, we choose subfamilies of $L$-functions that are zero-free close to 1. For these subfamilies, the $L$-functions have the extremal value at $s\,=\,1$, and by the class number formula, we obtain the extreme class numbers.

For a real quadratic field , let tk be the exact power of 2 dividing the class number hk of k and ηk the fundamental unit of k. The aim of this paper is to study tk and the value of Nk/ℚ(ηk). Various methods have been successfully applied to obtain results related to this topic. The idea of our work is to select a special circular unit ℰk of k and investigate C(k)=〈±ℰk 〉. We examine the indices [E(k):C(k)] and [C(k):CS (k)] , where E(k) is the group of units of k, and CS (k) is that of circular units of k defined by Sinnott. Then by using the Sinnott’s index formula [E(k):CS (k)]=hk, we obtain as much information about tk and Nk/ℚ (ηk) as possible.

We give an explicit treatment of cubic function fields of characteristic at least five. This includes an efficient technique for converting such a field into standard form, formulae for the field discriminant and the genus, simple necessary and sufficient criteria for non-singularity of the defining curve, and a characterization of all triangular integral bases. Our main result is a description of the signature of any rational place in a cubic extension that involves only the defining curve and the order of the base field. All these quantities only require simple polynomial arithmetic as well as a few square-free polynomial factorizations and, in some cases, square and cube root extraction modulo an irreducible polynomial. We also illustrate why and how signature computation plays an important role in computing the class number of the function field. This in turn has applications to the study of zeros of zeta functions of function fields.

In this paper, we generalize the Kučera's group-determinant formulae to obtain the real and relative class number formulae of any subfield of cyclotomic function fields with arbitrary conductor in the form of a product of determinants. From these formulae, we generalize the relative class number formula of Rosen and Bae-Kang and obtain analogous results of Tsumura and Hirabayashi for an intermediate field in the tower of cyclotomic function fields with prime power conductor.

We construct certain elements in the motivic cohomology group $H^3_{\mathcal{M}}(E\times E',\mathbb{Q}(2))$, where $E$ and $E'$ are elliptic curves over $\mathbb{Q}$. When $E$ is not isogenous to $E'$ these elements are analogous to circular units in real quadratic fields, as they come from modular parametrizations of the elliptic curves. We then find an analogue of the class-number formula for real quadratic fields, which specializes to the usual quadratic class-number formula when $E$ and $E'$ are quadratic twists.

AMS 2000 Mathematics subject classification: Primary 11F67; 14G35. Secondary 11F11; 11E45; 14G10

Assuming the generalized Riemann hypothesis (GRH) and Artin conjecture for Artin L-functions, we prove that there exists a totally real number field of any fixed degree (>1) with an arbitrarily large discriminant whose normal closure has the full symmetric group as Galois group and whose class number is essentially as large as possible. One ingredient is an unconditional construction of totally real fields with small regulators. Another is the existence of Artin L-functions with large special values. Assuming the GRH and Artin conjecture it is shown that there exist an Artin L-functions with arbitrarily large conductor whose value at s = 1 is extremal and whose associated Galois representation has a fixed image, which is an arbitrary nontrivial finite irreducible subgroup of GL(n, $\open C$;) with property GalT.

We derive lower bounds for the rank of Picard groups of modular varieties associated with natural congruence subgroups of the orthogonal group of an even lattice of signature (2, l). As an example we consider the Siegel modular group of genus 2. The analytic part of this paper also leads to certain class number identities.

We find a lower bound on the number of imaginary quadratic extensions of the function field ${{\mathbb{F}}_{q}}\left( T \right)$ whose class groups have an element of a fixed order.

More precisely, let $q\,\ge \,5$ be a power of an odd prime and let $g$ be a fixed positive integer $\ge \,3$. There are $\gg \,{{q}^{\ell \left( \frac{1}{2}+\frac{1}{g} \right)}}$ polynomials $D\,\in \,{{\mathbb{F}}_{q}}\left[ T \right]$ with $\deg \left( D \right)\,\le \,\ell $ such that the class groups of the quadratic extensions ${{\mathbb{F}}_{q}}\left( T,\,\sqrt{D} \right)$ have an element of order $g$.

Stark conjectured that given a positive integer h, there are only a finite number of CM-fields L with class number equal to h. We prove this conjecture for fields L of degree [ges ]6 whose normal closure is solvable.

We give explicit formulas for the 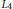${{L}_{4}}$ norm (or equivalently for the merit factors) of various sequences of polynomials related to the polynomials

$$f\left( z \right):=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n}{N} \right){{z}^{n}}.}$$

and

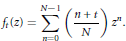$${{f}_{t}}(z)\,=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n+t}{N} \right){{z}^{n}}.}$$

where 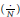$\left( \frac{.}{N} \right)$ is the Jacobi symbol.

Two cases of particular interest are when 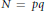$N\,=\,pq$ is a product of two primes and $p\,=\,q\,+\,2$ or 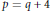$p\,=\,q\,+\,4$. This extends work of Høholdt, Jensen and Jensen and of the authors.

This study arises from a number of conjectures of Erdős, Littlewood and others that concern the norms of polynomials with −1, 1 coefficients on the disc. The current best examples are of the above form when 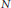$N$ is prime and it is natural to see what happens for composite 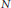$N$.

First, we prove that a non-abelian normal CM-field of degree 16 has odd relative class number if and only if it is dihedral, or is a compositum of two normal octic CM-fields with the same maximal real subfield, or has Galois group $G_9 =\langle a,b,z: a^2=b^2=z^4=1,b^{-1}ab=az^2,az=za,bz=zb\rangle$. Then, we solve several relative class number one problems. (1) We solve the relative class number one problem for the dihedral CM-fields of 2-power degrees. First, we remind the reader of the characterization of the dihedral CM-fields of 2-power degrees with odd relative class numbers. Second, we give lower bounds on relative class numbers of dihedral CM-fields of 2-power degrees with odd relative class numbers. We thus obtain an upper bound on the discriminants of the dihedral CM-fields of 2-power degrees with relative class number equal to 1. Third, we compute the relative class numbers of all the dihedral CM-fields of 2-power degrees with odd relative class numbers and discriminants less than or equal to this latter bound. We end up with a list of twenty-four dihedral CM-fields of 2-power degrees with relativeclass numbers equal to 1, and show that exactly twenty-one of them have class number 1. (2) We determine all the non-abelian normal CM-fields of degree 16 with Galois group $G_9$ which have relative class number 1 (there is only one such number field), and then those which have class number 1 (there is only one such number field). (3) We determine some of the non-abelian normal CM-fields $N =N_1N_2$ of degree 16 which are composita of two normal octic CM-fields $N_1$ and $N_2$ with the same maximal real subfield which have relative class number 1, and then those which have class number 1. Indeed, we focus on the case where one of the $N_i$ is a quaternion octic CM-field and prove that there is only one such compositum with relative class number 1 and that this compositum has class number 1.

1991 Mathematics Subject Classification: primary 11R29; secondary 11R21, 11R42, 11M20, 11Y40.

The jacobian variety of the Catalan curve $y^q = x^p - 1$ is shown to be nondegenerate. As an application, a 0-1-matrix whose determinant computes the relative class number of the $pq$-th cyclotomic field is constructed.

We provide a criterion for the class group of a complex quadratic field to have exponent at most 2. This is given in terms of the factorization of a generalized Euler-Rabinowitsch polynomial and has consequences for consecutive distinct initial prime-producing quadratic polynomials which we cite as applications.

In this paper, we use the Lagrange neighbour and our equivalence theorem for primitive ideals to obtain lower bounds which are sharper than those given in the literature for class numbers of real quadratic fields in general, but applied to greatest advantage when d is of ERD type.

Let h(m) denote the class number of the quadratic field Q(√m). In this paper necessary and sufficient conditions for h (m) to be divisible by 16 are determined when m = −p, where p is a prime congruent to 1 modulo 8, and when m = −2p, where p is a prime congruent to ±1 modulo 8.