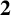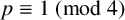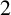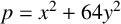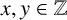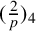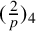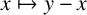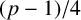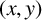1 Introduction
For an odd prime p, an integer a with
$(a,p)=1$
is called a quartic or biquadratic residue modulo p provided
$x^4\equiv a\pmod {p}$
is solvable. Clearly a is a quartic residue if and only if
$ a^{{(p-1)}/{4}}\equiv 1\pmod {p}.$
We need only consider
$p\equiv 1 \pmod {4}$
, since for
$p\equiv 3\pmod {4}$
, the quartic residues coincide with quadratic residues.
Concerning quartic residuacity of
$2$
modulo p, we may further assume
$p=8n+1$
so that
$(\frac 2p)=1$
. Then the quartic residue symbol
$(\frac {2}{p})_4 = \pm 1 $
is determined by the congruence
$(\frac {2}{p})_4 \equiv 2^{{(p-1)}/{4}} \pmod {p}.$
It was observed by Euler and first proved by Gauss [Reference Gauss5] via the law of quartic reciprocity (see [Reference Berndt, Evans and Williams2, Reference Ireland and Rosen7]) that
$$ \begin{align*} \bigg(\frac{2}{p}\bigg)_4 = 1 \iff p= x^2+64y^2\quad \mbox{for some } x,y \in \Bbb Z. \end{align*} $$
Barrucand and Cohn [Reference Barrucand and Cohn1] proved several more equivalences:
$$ \begin{align} (-1)^n \bigg(\frac{2}{p}\bigg)_4=1 &\iff \bigg(\frac{1+\sqrt{2} }{p}\bigg)=1 \iff (-1)^{ h(-4p)/4} =1\notag \\ &\iff p\!=\! a^2+32b^2\quad \mbox{for some } a,b \in \Bbb Z \notag \\ &\iff p\!=\!c^2-32d^2\quad \mbox{for some } c,d \in \Bbb Z \mbox{ with } |c|\equiv 1\pmod{4} \notag \\ &\iff p\!=\!e^2+16f^2\quad \mbox{with } e,f \in \Bbb Z \mbox{ and } (-1)^{{(e-1)}/2}e-1 \equiv 4f \pmod{8}. \end{align} $$
Here,
$h(-4p)$
is the class number of
$\Bbb Q(\sqrt {-p})$
and
$\sqrt {2}$
denotes any integer x satisfying
$x^2\equiv 2 \pmod {p}.$
(A simple proof for the last three expressions can be found in [Reference Williams10].) Hasse [Reference Hasse6] obtained a simple expression via the class number of
$\Bbb Q(\sqrt {-2p})$
:
$$ \begin{align} \bigg(\frac{2}{p}\bigg)_4 = (-1)^{h(-8p)/4}. \end{align} $$
(Note that (1.2) is related to (1.1) because
$h(-4p)+h(-8p)\equiv 4n \pmod {8}$
by [Reference Pizer9, Proposition 2].) Lehmer [Reference Lehmer8] modified the argument of Gauss’ lemma to prove
$$ \begin{align*} \bigg(\frac{2}{p}\bigg)_4= 1 \iff \bigg|\bigg\{1\leq x \leq \frac{p-1}{4} : \bigg( \frac{x}{p} \bigg)=-1\bigg\}\bigg| \equiv0 \pmod2. \end{align*} $$
Let
$\Bbb F_p$
denote the finite field with p elements. The Legendre symbol
$(\frac {a}{p})$
can be defined as the sign of the permutation of
$\Bbb F_p$
sending
$x \mapsto ax$
by Zolotarev’s theorem (see [Reference Conway3, Reference Dressler and Shult4]). Our aim is to find a simple permutation, the sign of which is determined by the quartic residuacity of
$2$
modulo p.
Assume
$p\equiv 1 \pmod {4}$
from now on. For such primes, there are nontrivial solutions to
$x^2+y^2\equiv 0\pmod {p}$
in
$\Bbb F_p^{*}$
. Moreover, for any x with
$1\leq x \leq (p-1)/2$
, there exists a unique y with
$1\leq y \leq (p-1)/2$
such that
$(x,y)$
is a solution. So there are
$(p-1)/4$
essentially different solutions. For example, for
$p=29$
, we need only consider seven pairs
$(x,y)$
with
$1\leq x < y \leq (p-1)/2$
:
$$ \begin{align} (1,12), \ (2,5), \ (3,7), \ (4,10), \ (6,14), \ (8,9), \ (11,13). \end{align} $$
Observe that the difference of the two numbers in any pair always gives the first component of another pair, that is,
$12-1=11, \ 13-11=2, \ 5-2=3 $
and so on. This observation leads to the following theorem.
Theorem 1.1. Let p be a prime with
$p\equiv 1\pmod {4}$
. Set
$$ \begin{align} A: = \{ (a,\tilde{a})\in \Bbb Z\times\Bbb Z: a^2+\tilde{a}^2\equiv 0 \pmod{p}, \quad 1\leq a <\tilde{a}\leq (p-1)/2 \}. \end{align} $$
Then we can define a permutation
$\psi _p$
of A by the rule
$a \mapsto \tilde {a}-a $
applied to the first component.
The theorem implies
$$ \begin{align*} \sum_{(a,\tilde{a})\in A} a = \sum_{(a,\tilde{a})\in A} (\tilde{a}-a) = \frac{1}{2} \sum_{(a,\tilde{a})\in A} \tilde{a}. \end{align*} $$
However,
$\{1,2,\ldots ,(p-1)/2\}$
is partitioned into
$(p-1)/4$
pairs in A. Thus
$$ \begin{align*} \sum_{(a,\tilde{a})\in A} (a+ \tilde{a}) = \sum_{x=1}^{(p-1)/2} x = \frac{p^2-1}{8}. \end{align*} $$
Thus we immediately obtain the next corollary.
Corollary 1.2. We have
$$ \begin{align*} \sum_{(a,\tilde{a})\in A} a = \frac{p^2-1}{24} \quad \mbox{and} \quad \sum_{(a,\tilde{a})\in A} \tilde{a} = \frac{p^2-1}{12}. \end{align*} $$
We now study the sign of
$\psi _p$
. Let
$\{x\}_p$
as usual denote the least nonnegative residue of x modulo p. Set
$i=\{\prod _{x=1}^{(p-1)/2}x\}_p$
so that
$i^2\equiv -1\pmod {p}$
by Wilson’s theorem.
We define
${\mathcal U}_4= \{\pm 1, \pm i\}$
. Then
$ \Bbb F_p^{*} / {\mathcal U}_4$
is a cyclic group of order
$(p-1)/4$
and multiplication by
$i-1$
induces a permutation
$\Psi _p$
of this quotient group. As an example, for
$p= 29$
again,
$i=\{14!\}_{29}=12$
. Thus
$\Psi _{29}$
is obtained from multiplication by 11 and can be illustrated by its action on cosets as follows:
$$ \begin{gather*} \hookrightarrow \begin{Bmatrix} 1 \\ 12 \\ 17 \\ 28 \end{Bmatrix} \mapsto \begin{Bmatrix} 11 \\ 13 \\ 16 \\ 18 \end{Bmatrix} \mapsto \begin{Bmatrix} 2 \\ 5 \\ 24 \\ 27 \end{Bmatrix} \mapsto \begin{Bmatrix} 3 \\ 7 \\ 22 \\ 26 \end{Bmatrix} \mapsto \begin{Bmatrix} 4 \\ 10 \\ 19 \\ 25 \end{Bmatrix} \mapsto \begin{Bmatrix} 6 \\ 14 \\ 15 \\ 23 \end{Bmatrix} \mapsto \begin{Bmatrix} 8 \\ 9 \\ 20 \\ 21 \end{Bmatrix} \mapsto \end{gather*} $$
Comparing this with (1.3), we see that the permutation
$\psi _p$
shows the behaviour of certain representatives in the cosets under
$\Psi _p$
. This is because for any pair
$(a,\tilde {a})\in A$
, we have
$\tilde {a}=\pm ia \pmod {p}.$
Hence the rule of
$\psi _p$
can be considered as
$a \mapsto \{\pm (\pm i-1)a\}_p$
. However, all the four possibilities
$\pm (i\pm 1)$
are in the same coset in
$ \Bbb F_p^{*} / {\mathcal U}_4$
, which implies that
$\psi _p$
induces
$\Psi _p$
in the quotient group. Hence they have the same sign.
Theorem 1.3. For a prime
$p\equiv 1\pmod {4}$
, define
$i=\{\prod _{x=1}^{(p-1)/2}x\}_p$
and
${\mathcal U}_4= \{\pm 1, \pm i\}$
. Then the sign of
$\psi _p$
in Theorem 1.1 is equal to that of
$\Psi _p$
, the permutation of
$ \Bbb F_p^{*} / {\mathcal U}_4$
induced by
$x \mapsto (i-1)x$
. Further
$$ \begin{align*} {{\mathrm{sign}}}\;(\psi_p)= {{\mathrm{sign}}}\;(\Psi_p)=\begin{cases} \displaystyle(-1)^{n} \bigg (\frac{2}{p} \bigg)_4 &\text{if} \ p=8n+1,\\ 1 &\text{if} \ p=8n+5. \end{cases} \\ \end{align*} $$
In other words,
$\psi _p$
is an odd permutation only in two cases:
-
(i)
$p\equiv 1\pmod {16}$
and
$2$
is a quartic nonresidue modulo p; -
(ii)
$p\equiv 9\pmod {16}$
and
$2$
is a quartic residue modulo p.
Now consider the mapping
$\tilde {a} \mapsto a+\tilde {a}$
. As in the argument before Theorem 1.3, it induces the same permutation
$\Psi _p$
. In view of Theorem 1.1,
$(a,\tilde {a})$
is sent by
$\psi _p$
to either
$(\tilde {a}-a, \ a+\tilde {a})$
or
$(\tilde {a}-a, \ p-(a+\tilde {a}) )$
, depending on which one belongs to A. This gives the next corollary.
Corollary 1.4. For an integer x, determine
$\|x\|_p $
as the unique integer such that
$0\leq \|x\|_p< p/2$
and
$ \| x \|_p \equiv \pm x \pmod {p}.$
Then the permutation
$\psi _p$
of A sends
$\tilde {a}$
to
$\|a+\tilde {a}\|_p$
applied to the second component.
Theorems 1.1 and 1.3 will be proved in the next two sections, respectively.
2 Proof of Theorem 1.1
Let i be defined as in Theorem 1.3 so that
$i^2\equiv -1 \pmod {p}$
and let
$\|x\|_p $
be as in Corollary 1.4. Clearly
$\|x\|_p = \|-x\|_p$
and
$\|xy\|_p = \|\,\|x\|_py\,\|_p$
. Define
$$ \begin{align*} {\mathcal V}_p:=\bigg\{1\leq x\leq \frac{p-1}{2}:\, x<\|ix\|_p\bigg\}. \end{align*} $$
Clearly
$ |{\mathcal V}_p|={(p-1)}/{4}.$
For each
$a\in \{1,\ldots ,(p-1)/2\}$
, we set
$\tilde {a}:=\|ia\|_p.$
In view of the definition of A in (1.4), we have
$\{(a,\tilde {a}): a\in {\mathcal V}_p\}=A $
.
For convenience, we use the same
$\psi _p$
for the mapping
$a\mapsto \tilde {a}-a$
with domain
${\mathcal V}_p$
. It suffices to prove that
$\psi _p$
is a permutation of
${\mathcal V}_p$
. First we show that
$\psi _p({\mathcal V}_p)\subseteq {\mathcal V}_p$
. As
$\tilde {a}=\|ia\|_p$
, we partition
${\mathcal V}_p$
into
$V_1\cup V_2$
, where
$$ \begin{align*}V_1:=\{a\in{\mathcal V}_p:\,\tilde{a}=\{ia\}_p \} \quad\mbox{and}\quad V_2:=\{a\in{\mathcal V}_p:\,\tilde{a}= p-\{ia\}_p\}. \end{align*} $$
For
$a\in V_1$
, we have
$a< \tilde {a} =\{ia\}_p\leq (p-1)/2$
and hence
$$ \begin{align*}\psi_p(a)=\{i a\}_p-a=\{(i-1) a\}_p. \end{align*} $$
Furthermore, as
$i^2\equiv -1\pmod {p}$
,
$$ \begin{align*}\|i \psi_p(a)\|_p=\|i(i-1)a)\|_p=\|(i+1)a\|_p. \end{align*} $$
To show
$\psi _p(a)\in {\mathcal V}_p$
, we need to verify
$$ \begin{align} \{(i-1) a\}_p<\|(i+1)a\|_p. \end{align} $$
If
$\{ (i+1) a \}_p> p/2$
, then
$$ \begin{align*}\{(i-1)a\}_p < \{i a\}_p = \tilde{a} < \{(i+1)a\}_p.\end{align*} $$
Thus
$$ \begin{align*}\{(i+1)a\}_p + \{(i-1)a\}_p = 2\{i a\}_p =2\tilde{a} < p.\end{align*} $$
Then (2.1) holds since
$$ \begin{align*}\|{(i+1)a}\|_p = p - \{(i+1)a\}_p> \{(i-1)a\}_p.\end{align*} $$
If
$\{(i+1)a\}_p < p/2$
, then (2.1) is also true since
$$ \begin{align*}\|{(i+1)a}\|_p = \{(i+1)a\}_p = \{ 2a+ (i-1)a \}_p = 2a + \{(i-1)a\}_p> \{(i-1)a\}_p.\end{align*} $$
Therefore,
$\psi _p(V_1)\subseteq {\mathcal V}_p$
. Using a similar argument,
$\psi _p(V_2)\subseteq {\mathcal V}_p$
. Thus it suffices to show that
$\psi _p$
is an injection to prove the theorem.
Assume, on the contrary, there exist distinct
$a_1,a_2\in {\mathcal V}_p$
such that
$\psi _p(a_1)=\psi _p(a_2)$
. If
$a_1,a_2 \in V_1$
, then
$a_1 \not \equiv a_2 \pmod {p}$
and
$\{(i-1)a_1\}_p = \{(i-1)a_2\}_p,$
which is evidently impossible. Similarly,
$a_1,a_2\in V_2$
is impossible. So we may assume that
$a_1\in V_1$
and
$a_2\in V_2$
, that is,
$\tilde {a}_1\equiv ia_1\pmod {p}$
and
$\tilde {a}_2\equiv -ia_2\pmod {p}$
. Then
$$ \begin{align*}(i-1)a_1\equiv \psi_p(a_1)=\psi_p(a_2)\equiv (-i-1)a_2\equiv i(i-1)a_2\pmod{p}. \end{align*} $$
It follows that
$$ \begin{align*}a_1\equiv i a_2\equiv-\tilde{a}_2\pmod{p}, \end{align*} $$
which contradicts the fact that
$1\leq a_1,\tilde {a}_2\leq (p-1)/2$
.
Thus
$\psi _p$
is an injection and the proof is complete.
3 Proof of Theorem 1.3
Since
$\Bbb F_p^{*}$
is cyclic,
$\Bbb F_p^{*} / {\mathcal U}_4$
is also a cyclic group and of order
$(p-1)/4$
. Let the order of the coset of
$1+i$
be m. Then
$\Psi _p$
is composed of
$(p-1)/4m$
disjoint cycles of length m. Thus
$$ \begin{align} {{\textrm{sign}}}\;(\psi_p) = (-1)^ {{(m-1)(p-1)}/{4m}}. \end{align} $$
Now we divide the discussion into five cases.
Case (i):
$p\equiv 1\pmod {16}$
and
$2$
is a quartic residue modulo p.
Case (ii):
$p\equiv 9\pmod {16}$
and
$2$
is a quartic nonresidue modulo p.
In these two cases,
$$ \begin{align*} [(1+i)^{{(p-1)}/{8}}]^4 \equiv (-4)^{{(p-1)}/{8}} \equiv (-1)^{{(p-1)}/8}2^{{(p-1)}/4} \equiv 1 \pmod{p}, \end{align*} $$
which implies
$(1+i)^{{(p-1)}/{8}} \in {\mathcal U}_4$
. Hence
$(p-1)/8$
is divisible by m and
$\psi _p$
is even from (3.1).
Case (iii):
$p\equiv 1\pmod {16}$
and
$2$
is a quartic nonresidue modulo p.
Case (iv):
$p\equiv 9\pmod {16}$
and
$2$
is a quartic residue modulo p.
In these two cases,
$$ \begin{align*} [(1+i)^{{(p-1)}/{8}}]^4 \equiv (-4)^{{(p-1)}/{8}} \equiv (-1)^{{(p-1)}/8}2^{{(p-1)}/4} \equiv -1 \pmod{p}. \end{align*} $$
Therefore,
$(1+i)^{{(p-1)}/4}\in {\mathcal U}_4$
while
$(1+i)^{{(p-1)}/8} \not \in {\mathcal U}_4$
. In other words, m, a factor of
$(p-1)/4$
, does not divide
$(p-1)/8$
. So
$q=(p-1)/4m$
must be odd while m is even. Thus
$\psi _p$
is odd from (3.1).
Case (v):
$p\equiv 5\pmod {8}$
. Now m must be odd since it divides
$(p-1)/4$
from the definition. Thus
${{\textrm {sign}}}\;\psi _p=1$
in view of (3.1). The proof is complete.□
Acknowledgements
We are deeply grateful to the anonymous referee, whose valuable suggestions enabled us to simplify our proof substantially. We would also like to thank Professor Zhi-Wei Sun for his guidance.
