For a given list assignment 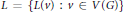 $L\,=\,\{L\left( v \right)\,:\,v\,\in \,V\left( G \right)\}$, a graph
$L\,=\,\{L\left( v \right)\,:\,v\,\in \,V\left( G \right)\}$, a graph 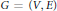 $G\,=\,\left( V,\,E \right)$ is
$G\,=\,\left( V,\,E \right)$ is  $L$-colorable if there exists a proper coloring
$L$-colorable if there exists a proper coloring  $c$ of
$c$ of 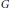 $G$ such that
$G$ such that 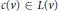 $c\left( v \right)\,\in \,L\left( v \right)$ for all
$c\left( v \right)\,\in \,L\left( v \right)$ for all 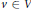 $v\,\in \,V$. If
$v\,\in \,V$. If 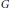 $G$ is
$G$ is  $L$-colorable for every list assignment
$L$-colorable for every list assignment  $L$ having
$L$ having 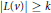 $\left| L\left( v \right) \right|\,\ge \,k$ for all
$\left| L\left( v \right) \right|\,\ge \,k$ for all 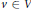 $v\,\in \,V$, then
$v\,\in \,V$, then 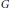 $G$ is said to be
$G$ is said to be  $k$-choosable. Montassier (Inform. Process. Lett. 99 (2006) 68-71) conjectured that every planar graph without cycles of length 4, 5, 6, is 3-choosable. In this paper, we prove that every planar graph without 5-, 6- and 10-cycles, and without two triangles at distance less than 3 is 3-choosable.
$k$-choosable. Montassier (Inform. Process. Lett. 99 (2006) 68-71) conjectured that every planar graph without cycles of length 4, 5, 6, is 3-choosable. In this paper, we prove that every planar graph without 5-, 6- and 10-cycles, and without two triangles at distance less than 3 is 3-choosable.