We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
$(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
Let 
$\mathbb {F}$ be a field and 
$(s_0,\ldots ,s_{n-1})$ be a finite sequence of elements of 
$\mathbb {F}$. In an earlier paper [G. H. Norton, ‘On the annihilator ideal of an inverse form’, J. Appl. Algebra Engrg. Comm. Comput. 28 (2017), 31–78], we used the 
$\mathbb {F}[x,z]$ submodule 
$\mathbb {F}[x^{-1},z^{-1}]$ of Macaulay’s inverse system 
$\mathbb {F}[[x^{-1},z^{-1}]]$ (where z is our homogenising variable) to construct generating forms for the (homogeneous) annihilator ideal of 
$(s_0,\ldots ,s_{n-1})$. We also gave an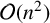 
$\mathcal {O}(n^2)$ algorithm to compute a special pair of generating forms of such an annihilator ideal. Here we apply this approach to the sequence r of the title. We obtain special forms generating the annihilator ideal for 
$(r_0,\ldots ,r_{n-1})$ without polynomial multiplication or division, so that the algorithm becomes linear. In particular, we obtain its linear complexities. We also give additional applications of this approach.
