We introduce a novel amortised resource analysis couched in a type-and-effect system. Our analysis is formulated in terms of the physicist’s method of amortised analysis and is potentialbased. The type system makes use of logarithmic potential functions and is the first such system to exhibit logarithmic amortised complexity. With our approach, we target the automated analysis of self-adjusting data structures, like splay trees, which so far have only manually been analysed in the literature. In particular, we have implemented a semi-automated prototype, which successfully analyses the zig-zig case of splaying, once the type annotations are fixed.

von Neumann [(1951). Various techniques used in connection with random digits. National Bureau of Standards Applied Math Series 12: 36–38] introduced a simple algorithm for generating independent unbiased random bits by tossing a (possibly) biased coin with unknown bias. While his algorithm fails to attain the entropy bound, Peres [(1992). Iterating von Neumann's procedure for extracting random bits. The Annals of Statistics 20(1): 590–597] showed that the entropy bound can be attained asymptotically by iterating von Neumann's algorithm. Let $b(n,p)$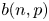 denote the expected number of unbiased bits generated when Peres’ algorithm is applied to an input sequence consisting of the outcomes of $n$ 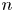tosses of the coin with bias $p$. With $p=1/2$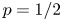, the coin is unbiased and the input sequence consists of $n$ 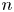unbiased bits, so that $n-b(n,1/2)$ 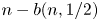may be referred to as the cost incurred by Peres’ algorithm when not knowing $p=1/2$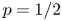. We show that $\lim _{n\to \infty }\log [n-b(n,1/2)]/\log n =\theta =\log [(1+\sqrt {5})/2]$ 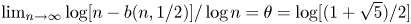(where $\log$ 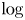is the logarithm to base $2$), which together with limited numerical results suggests that $n-b(n,1/2)$ may be a regularly varying sequence of index $\theta$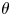. (A positive sequence $\{L(n)\}$ is said to be regularly varying of index $\theta$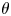 if $\lim _{n\to \infty }L(\lfloor \lambda n\rfloor )/L(n)=\lambda ^\theta$ 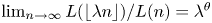for all $\lambda > 0$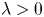, where $\lfloor x\rfloor$ 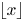denotes the largest integer not exceeding $x$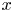.) Some open problems on the asymptotic behavior of $nh(p)-b(n,p)$ 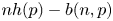are briefly discussed where $h(p)=-p\log p- (1-p)\log (1-p)$ denotes the Shannon entropy of a random bit with bias $p$.

We investigate the average similarity of random strings as captured by the average number of ‘cousins’ in the underlying tree structures. Analytical techniques including poissonization and the Mellin transform are used for accurate calculation of the mean. The string alphabets we consider are m-ary, and the corresponding trees are m-ary trees. Certain analytic issues arise in the m-ary case that do not have an analog in the binary case.