In an earlier paper, Romanowska, Ślusarski and Smith described a duality between the category of polytopes (finitely generated real convex sets considered as barycentric algebras) and a certain category of intersections of hypercubes, considered as barycentric algebras with additional constant operations. The present paper provides an extension of this duality to a much more general class of so-called quasipolytopes, that is, convex sets with polytopes as closures. The dual spaces of quasipolytopes are Płonka sums of open polytopes, which are considered as barycentric algebras with some additional operations. In constructing this duality, we use several known and new dualities: the Hofmann–Mislove–Stralka duality for semilattices; the Romanowska–Ślusarski–Smith duality for polytopes; a new duality for open polytopes; and a new duality for injective Płonka sums of polytopes.

In this paper we prove a commutative algebraic extension of a generalized Skolem–Mahler– Lech theorem. Let 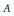$A$ be a finitely generated commutative $K$–algebra over a field of characteristic 0, and let $\sigma$ be a $K$–algebra automorphism of 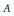$A$. Given ideals 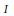$I$ and 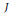$J$ of 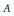$A$, we show that the set 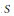$S$ of integers $m$ such that 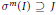${{\sigma }^{m}}(I)\,\supseteq \,J$ is a finite union of complete doubly infinite arithmetic progressions in $m$, up to the addition of a finite set. Alternatively, this result states that for an affine scheme 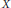$X$ of finite type over $K$, an automorphism $\sigma \,\in \,\text{Au}{{\text{t}}_{k}}(X)$, and $Y$ and $Z$ any two closed subschemes of 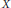$X$, the set of integers $m$ with 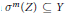${{\sigma }^{m}}(Z)\,\subseteq \,Y$ is as above. We present examples showing that this result may fail to hold if the affine scheme 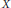$X$ is not of finite type, or if 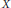$X$ is of finite type but the field $K$ has positive characteristic.

We strengthen certain results concerning actions of $\left( \mathbb{C},\,+ \right)$ on ${{\mathbb{C}}^{3}}$ and embeddings of ${{\mathbb{C}}^{2}}$ in ${{\mathbb{C}}^{3}}$, and show that these results are in fact valid over any field of characteristic zero.