This paper provides an assessment of current rotor design comparison practices. First, the employed CFD method is validated for a number of rotor designs and is shown to achieve accurate performance predictions in hover and high-speed forward flight. Based on CFD results, a detailed investigation is performed in terms of comparing different rotor designs. The CFD analysis highlighted the need of high fidelity methods due to the subtle aerodynamics involved in advanced planforms. Nevertheless, the paper suggests that the correct basis for comparison in terms of performance metrics must be used to inform decisions about the suitability of the rotor blades designs for specific applications. In particular, when comparing blades of advanced planforms, direct torque and thrust comparisons are better than the commonly used lift to drag ratio and figure of merit.

It is shown that 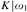$K|{\omega _1}$ need not be solid in the sense previously introduced by the authors: it is consistent that there is no inner model with a Woodin cardinal yet there is an inner model W and a Cohen real x over W such that 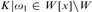$K|{\omega _1}\,\, \in \,\,W[x] \setminus W$. However, if 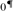${0^{\rm{\P}}}$ does not exist and 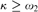$\kappa \ge {\omega _2}$ is a cardinal, then 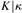$K|\kappa$ is solid. We draw the conclusion that solidity is not forcing absolute in general, and that under the assumption of 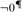$\neg {0^{\rm{\P}}}$, the core model is contained in the solid core, previously introduced by the authors.

It is also shown, assuming 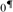${0^{\rm{\P}}}$ does not exist, that if there is a forcing that preserves 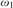${\omega _1}$, forces that every real has a sharp, and increases 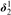$\delta _2^1$, then 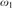${\omega _1}$ is measurable in K.