NOMENCLATURE

Latin

a

speed of sound

A

rotor disk area

AR

aspect ratio, $R/c_{ref}$

c

rotor chord

$c_{ref}$

reference rotor chord (first aerodynamic section)

$C_p$

pressure coefficient, $(p - p_\infty)/(1/2\rho(\Omega r/R)^2)$

$C_D$

drag coefficient, $D/(\rho (\Omega R)^2 \pi R^2)$

$C_f$

skin friction coefficient, $\tau_w/(1/2\rho(\Omega r/R)^2)$

$C_L$

lift coefficient, $L/(\rho (\Omega R)^2 \pi R^2)$

$C_q$

blade section torque coefficient, $dT/dr \times 2/(\rho c_{ref} (\Omega r)^2)$

$C_Q$

torque coefficient, $Q/(\rho (\Omega R)^2 \pi R^3)$

$C_t$

blade section thrust coefficient, $dQ/dr \times 2/(\rho c_{ref}R(\Omega r)^2)$

$C_T$

thrust coefficient, $T/(\rho (\Omega R)^2 \pi R^2)$

D

drag force

DL

disk loading, $T/A$

FoM

figure of merit, $C_T^{3/2}/(\sqrt{2}C_Q)$

L

rotor lift

L/D

lift to drag ratio, $C_L/C_Q \mu$

$(L/D)_e$

equivalent lift to drag ratio, $C_L/(C_Q/\mu - C_D)$

$N_b$

number of blades

M

Mach number, $V_\infty / a_\infty$

$M_{TIP}$

blade tip Mach number, $\Omega R / a_\infty$

p

pressure

P

rotor power

PL

power loading, $W/P$

Q

rotor torque

r

local radial position

R

rotor radius

R

flow equation residual vector

T

rotor thrust

V

velocity

V

flow equation cell volume

W

flow equation solution vector

W

weight

$y^+$

dimensionless wall distance

Greek

$\alpha_s$

shaft angle

$\beta_0$

coning angle

$\beta_{1s},\beta_{1c}$

flapping harmonics

$\mu$

rotor advance ratio, $M_{\infty}/M_{TIP}$

$\Omega$

rotor rotational speed

$\psi$

azimuthal angle

$\rho$

density

$\sigma_N$

nominal rotor solidity, $\sigma_{N}=N_b/(\pi R/c_{ref})$

$\sigma_G$

geometric rotor solidity, $\sigma_G = \int_{0}^{1} \sigma(r) dr$

$\sigma_T$

thrust-weighted rotor solidity, $\sigma_T = 3\int_{0}^{1} \sigma(r)r^2 dr$

$\theta_0$

collective angle

$\Theta$

blade linear twist angle

$\theta_{1s},\theta_{1c}$

pitching harmonics

Acronyms

ACRB

Advanced Chinook Rotor Blade

ALE

Arbitrary Langrangian-Eulerian

BERP

British Experimental Rotor Programme

BILU

Block Incomplete Lower-Upper

CFD

Computational Fluid Dynamics

HMB3

Helicopter Multi-Block v3.0

LBERP

Langley BERP rotor blade

LBL

Langley Baseline rotor blade

LBLs

Langley Baseline (scaled) rotor blade

MUSCL

Monotonic Upwind Scheme for Conservation Laws

NFAC

National Full-Scale Aerodynamics Complex (at NASA Ames)

PSP

Pressure Sensitive Paint rotor blade

URANS

Unsteady Reynolds Averaged Navier-Stokes

Subscripts and superscripts

ref

reference

i,j,k

cell index

*

sonic

$\infty$

freestream

2.0 CFD METHOD

The Helicopter Multi-Block (HMB3)^{(Reference Steijl, Barakos and Badcock11,Reference Steijl and Barakos12)} code of Glasgow University is used within this study. The HMB3 code solves the Unsteady Reynolds Averaged Navier–Stokes (URANS) equations in integral form using the Arbitrary Lagrangian Eulerian (ALE) formulation for time-dependent domains, which may include moving boundaries. The Navier–Stokes equations are discretised using a cell-centred finite volume approach on a multi-block structured grid. The spatial discretisation of these equations leads to a set of ordinary differential equations in time,

(1)\begin{eqnarray}\frac{d}{dt} ({\bf W}_{i,\,j,\,k}\ V_{i,\,j,\,k}) = - {{\bf R}}_{i,\,j,\,k}({\bf W})\end{eqnarray}

where i, j, k represent the cell index, W and R are the vector of conservative flow variables and flux residual respectively, and $V_{i,\,j,\,k}$ is the volume of the cell i, j, k. To evaluate the convective fluxes, the Osher^{(Reference Osher and Chakravarthy13)} approximate Riemann solver is used, while the viscous terms are discretised using a second order central differencing spatial discretisation. The Monotone Upstream-centred Schemes for Conservation Laws, which is referred to in the literature as the MUSCL approach and developed by Leer^{(Reference van Leer14)}, is used to provide high-order accuracy in space. The HMB solver uses the alternative form of the Albada limiter^{(Reference van Albada, van Leer and Roberts15)} activated in regions where a large gradients are encountered mainly due to shock waves, avoiding non-physical spurious oscillations. An implicit dual-time stepping method is employed to perform the temporal integration, where the solution is marching in pseudo-time iterations to achieve fast convergence, which is solved using a first-order backward difference. The linearised system of equations is solved using the Generalised Conjugate Gradient method with a Block Incomplete Lower-Upper (BILU) factorisation as a pre-conditioner^{(Reference Axelsson16)}. To allow an easy sharing of the calculation load on parallel computers, multi-block structured meshes are used^{(Reference Woodgate and Barakos17)}.

3.0 BLADE GEOMETRIES

Four blade planforms, shown in Fig. 1 are the subject of this study: the Langley Baseline blade (LBL) with a rectangular planform, the Langley BERP blade (LBERP) with a paddle-shaped tip and the PSP blade with a swept-tapered blade tip and a scaled Langley Baseline blade (LBLs) to examine solidity effects.

Figure 1. Planform geometries of the Langley Baseline (nominal and scaled), Langley BERP and PSP blades scaled to a chord of 1.0 with a radius equal to the blade aspect ratio.

The LBERP and LBL blades were tested by Yeager et al^{(Reference Yeager, Noonan, Singleton, Wilbur and Mirick6)} at model scale in a Freon-12 medium with a higher density than air. This allowed tests closer to full scale Reynolds numbers. The two blades tested have the same radius, aerofoils and twist distribution. Both blades have a linear twist of approximately $-9$ degrees, with a constant blade twist outboards of 0.866R. A RC(4)-10 aerofoil section is used inboards up to 0.84R, whereas the tip section used from 0.866R is the RC(3)-07 aerofoil. The aerodynamics of these two aerofoils are described by Noonan^{(Reference Noonan18,Reference Noonan19)} . A linear transition was assumed between the two aerofoil sections. The main difference between the two blades is in the blade tip shape. The chord of the blade with the rectangular planform, referred to as the LBL blade is also increased by 9% compared to the LBERP blade with the paddle-shaped blade tip. This was done to match the thrust weighted solidities of the two blades, leading to slightly different aspect ratios of the two blades (13.76 for LBERP and 12.62 for LBL). As stated previously, the matching of thrust weighted solidity may favour the LBL blade, due to higher geometric solidity (0.101 for LBL compared to 0.096 for the LBERP blade), based on the findings of Perry^{(Reference Perry1)}. For this reason, an additional geometry was generated, the scaled LBL blade (LBLs). The same reference chord (inboard chord value) as for the LBERP was used for this design, hence the nominal solidity was matched. For the LBERP blade, a number of geometric uncertainties exist such as the exact blade tip shape and thickness distribution across the blade tip. The RC(3)-07 aerofoil was used up to 0.945R and then the thickness was tapered off linearly to an assumed trailing edge thickness of 0.04% c.

The PSP (Pressure Sensitive Paint) rotor blade was also tested at model scale by Wong et al^{(Reference Wong, Watkins, Goodman, Crafton, Forlines, Goss, Gregory and Juliano10)}, and has fewer geometric uncertainties than the LBERP blade. This model-scale blade was developed to test the PSP technique for rotor blades, hence the name “PSP blade”. The rotor blade has a linear blade twist of -14 degrees and a geometric solidity of 0.1033. The blade planform was generated using three radial stations. First, the RC(4)-12 aerofoil was used up to 65% R. Then, the RC(4)-10 aerofoil from 70% R to 80% R. Finally, the RC(6)-08 aerofoil was used from 85% R to the tip. The planform of the PSP model rotor has a 60% tapered and $30^\circ$ swept tip.

The differences in the rotor geometric properties are shown in Table 1. The simulated blade tip Mach numbers are also presented.

Table 1 Differences in the rotor designs geometric properties along with the simulated blade tip Mach numbers

Based on the geometric properties, a few observations can be made. Firstly, solely based on the definition of thrust coefficient ($T=C_T \rho(\Omega R)^2 \pi R^2$), the simulated blade designs will produce very different values of net thrust at the same thrust coefficient. This is due to the different blade tip Mach numbers and blade aspect ratios alone, hence not accounting for solidity effects or the planform shape. The LBERP blade produces 19% more net thrust than the LBL blade and 49% more net thrust than the PSP blade at a constant thrust coefficient and assuming a unit chord length. The net thrust produced by the LBERP and LBLs blades is equal. These aspects must be taken into account when comparing the different designs. Regarding, solidity effects, the nominal solidity is based solely on the reference blade chord and blade radius and does not take into account variation of chord along the blade radius. The geometric solidity considers the advanced planform shape, whereas the thrust-weighted solidity, as stated previously, provides a higher weighting of blade area located further outboards, hence the $r^2$ term in the integral. As can be seen from the geometric properties, the thrust-weighted solidities of the LBL and LBERP blades are matched, whereas the nominal solidity is matched for the LBERP and LBLs blades. Due to the different blade solidities, disk loadings and blade tip Mach numbers, comparison of the blade designs using standard performance metrics may not be possible, as analysed in Section 6, Rotor Design Comparison.

The analysis in further sections is aimed at comparing the different rotor designs scaled to the same rotor diameter. For the LBL and LBERP blades, this will be performed at matched thrust-weighted solidity as well as matched nominal solidity to examine solidity effects. The investigation will assess hover and high-speed forward flight to determine the performance benefits of each design and will possibly lead to a refined understanding of the impact of tip effects and the use of commonly used parameters such as figure of merit, lift to drag ratio and thrust-weighted solidity.

4.0 COMPUTATIONAL SETUP

For all cases, the Chimera meshing technique was used, and the flow field was computed for isolated rotors. The boundary layer was assumed to be fully turbulent, with the $k\omega$-SST turbulence model used to close the RANS equations and aeroelastic effects neglected. This assumption is valid as the experiments for all the examined rotor blades were performed at model scale, for fairly stiff blades, hence aeroelastic effects are not expected to be significant. In hover, to minimise computational costs a steady-state approach was used. A quarter of the rotor disk was modelled, with periodic boundary conditions in the azimuthal direction. This assumption is valid if the wake generated by the rotor can be considered as periodic and the blades do not experience deep stall. A source/sink model was used for the simulations with Froude boundary conditions imposed at the inflow and outflow. A typical computational domain is shown in Fig. 2. In forward flight, the full rotor disk with four blades was simulated as the flow is unsteady. A hub was also included in the computational domain and modelled as a generic ellipsoidal surface. In forward flight a matrix trimming method was used to achieve the target thrust coefficient while minimising rolling and yawing moments, with the full description found in Ref. (Reference Steijl, Barakos and Badcock11). For the blades, a C-topology around the leading edge of the blade was selected, whereas an H-topology was employed at the trailing edge. For the LBERP blade, an O-grid is used around the tip of the blade. The topologies of the meshes for the three blades are shown in Fig. 2.

Figure 2. Computational domain in hover and blade mesh topologies for the LBL, LBERP and PSP blades (hover). (a) Computational domain. (b) PSP blade blocking. (c) LBERP blade blocking. (d) LBL blade blocking.

The LBLs blade grid was generated by scaling the LBL grid in the spanwise direction. In forward flight, a coarser blade grid was generated for the PSP blade to minimise computational costs, whereas the same grids were used for the LBL and LBERP blades as in hover. The background grids have a non-uniform spacing with a clustering in the regions of the tip vortex and preceding blade tip vortices. Grid stretching is also employed towards the CFD domain boundaries. As these regions are far away from the rotor disk grid streching has a negligible impact on the overall solution. This leads to grid sizes of 10–12 million cells in hover and 32–45 million cells in forward flight. The detailed mesh properties for each of the rotor blades are presented in Table 2. For each of the blade grids, a wall distance of $1.0 \times 10^{-5}$$c_{ref}$ was used, which ensured a $y^+ < 1$.

Table 2 Grid sizes in millions of cells for the simulated rotor blades in hover and forward flight with mesh points in the chordwise, spanwise and normal directions

For our simulations, each of the blades is scaled to a root chord of 1, hence the LBL blade is simulated for a 9% lower radius compared to the LBERP blade. The LBLs blade has the same radius as the LBERP blade. The LBL and LBERP blades were tested at a blade tip Mach number of 0.628 with a Reynolds number (based on tip speed) of $2.51 \times 10^6$ for the LBERP and $2.74 \times 10^6$ for the LBL blades accounting for the properties of the Freon gas. The PSP rotor blade was simulated at a lower blade tip Mach number of 0.58 and Reynolds number, based on the reference blade chord $c_{ref}$ of 5.45 inches and on the blade-tip speed, equal to $1.94 \times 10^6$. The computed test cases are shown in Table 3.

Table 3 Computational cases in hover and forward flight for the LBERP, LBL, LBLs and PSP blades

As seen from Table 3, the simulated test cases are split into three sections. For CFD validation, a collective sweep is performed in hover. In forward flight, the LBERP and LBL blades are simulated in high-speed forward flight, whereas a thrust-sweep at $\mu=0.35$ is performed for the PSP rotor blade due to available experimental surface pressure data. For analysis of solidity effects, the results from the CFD validation are used for the LBL and LBERP blades, with the same simulations performed for the LBLs blade. For a more in depth comparison, the three blades (LBL, LBERP and PSP) are trimmed to the same thrust coefficient, $C_T=0.008$. The results at $13.5^\circ$ collective are also compared for the LBL and LBERP blades. In forward flight, an additional simulation is performed for the PSP blade, to match the high-speed conditions simulated for the LBL and LBERP blades.

5.0 RESULTS AND DISCUSSION – CFD VALIDATION

This section presents comparisons of the CFD predictions with experimental data. In hover, performance predictions are obtained for all three blade designs and compared with experimental data. In forward flight, integrated loads are only available for the Langley blades, however the surface pressure predictions on the advancing and retreating blades are presented for the PSP blade. The hover performance predictions and comparisons with experimental data for the three blades are shown in Figs. 3–4.

The hover performance predictions show very good agreement with experimental data for all three simulated blades. For the LBERP and LBL blades, the CFD FoM curves fit well within the experimental data scatter. The calibration accuracies are reported in Ref. (Reference Yeager, Noonan, Singleton, Wilbur and Mirick6), although the scatter in the experimental data points is larger. The main benefit of the LBERP blade is seen, where no significant performance loss can be observed at higher blade loading. Over the operational range of blade loadings for light/medium-weight helicopters the LBERP blade does not achieve the FoM of the LBL blade. At high thrust coefficients, the performance of the LBERP blade surpasses the LBL blade. This is in agreement with literature^{(Reference Perry1,Reference Robinson and Brocklehurst21,Reference Brocklehurst and Barakos22)} . The LBERP blade is able to operate at high loading conditions without major losses in thrust, making it well suited to heavy-lift applications. The LBERP blade also has a lower geometric solidity when compared to the rectangular blade. As can be seen in the performance results, at each collective, the LBERP blade has a higher $C_T/\sigma$, which is especially visible at higher loading. Regarding the accuracy of the CFD results, it can be claimed that the use of the steady-state method is sufficient here, since no extensive stall is detected. The experimental data scatter is larger than the difference between CFD and experiments. Therefore increasing the simulation fidelity, through the use of higher order numerical schemes or more advanced turbulent models does not lead to firmer conclusions. Higher fidelity simulations could only be justified when comparing with experimental data sets with fewer uncertainties.

For the PSP blade, very good predictions are also obtained when compared with experimental data. The experimental PSP blade measurement accurracy is reported in Ref. (Reference Overmeyer and Martin20), with FoM uncertainties approaching $\pm1$ counts at low thrust, and reducing to $\pm0.5-0.75$ counts at high thrust. Excellent agreement can be seen for low and medium thrust levels, with a minor underprediction of approximately two counts in FoM at high thrust. This occurs as a result of modelling the rotor as isolated. The inclusion of the fuselage employed during experiments, improves the FoM by 1.4 counts when compared to an isolated rotor at $C_T/\sigma=0.094$, as found by Jain^{(Reference Jain23)}. This shows that modelling installation effects is important for accurate hover predictions, especially at high blade loading. Blade surface pressure predictions are also available for the PSP rotor blade in hover at four thrust coefficients and were presented previously^{(Reference Fitzgibbon, Jimenez-Garcia, Woodgate and Barakos24)}. Unfortunately, no further data is available for CFD hover validation for these blades. For in-depth CFD validation, quantities such as surface pressure, sectional loads and vortex properties must be measured. Compensating errors may be present in the comparisons between CFD predictions and experimental data leading to a false sense of good agreement. The first step will be the future PSP tests in the large NASA NFAC wind tunnel facility, which will provide a comprehensive data set for CFD validation. However, further testing is required for more advanced planforms.

Figure 3. Hover performance predictions for the LBERP and LBL blades and comparisons with experimental data from Yeager et al^{(Reference Yeager, Noonan, Singleton, Wilbur and Mirick6)}.

Figure 4. Hover performance predictions for the PSP rotor blade, and comparison with experimental data from Overmeyer and Martin^{(Reference Overmeyer and Martin20)}.

The three blades are also simulated in high speed forward flight. Predictions of the integrated loads for the LBERP and LBL geometries are presented in Table 4.

Table 4 Integrated loads predictions for the LBERP and LBL blades in forward flight and comparisons with experimental data from Yeager et al^{(Reference Yeager, Noonan, Singleton, Wilbur and Mirick6)}

Very good agreement can be seen for both blades with experimental data. The predicted performance of the LBERP blade is further away from experiment due to a higher degree of geometric uncertainty^{(Reference Fitzgibbon, Jimenez-Garcia, Woodgate and Barakos24)}. Aeroelastic effects may also be more significant for the LBERP blade at high advance ratio, due to the advanced planform shape. Furthermore, the experimental trim states for these cases were unknown. Unfortunately, no further data is available for further validation of the CFD results for these blades. These results are analysed further in the section focused on rotor designs comparisons. For further validation of the CFD code for forward flight simulations, the PSP blade forward flight results are analysed at $\mu=0.35$ and three thrust coefficients of $C_T$ = 0.004, 0.006 and 0.008. Integrated loads are not available for these cases, however, surface pressure data was measured by Wong et al^{(Reference Wong, Watkins, Goodman, Crafton, Forlines, Goss, Gregory and Juliano10)}. The surface pressure predictions for the advancing and retreating blade sides are shown in Fig. 5.

Figure 5. Surface pressure predictions for the PSP blade in forward flight at three thrust levels. Comparisons are shown for the upper surface of the rotor at $\textit{r/R}\,\text{=\,0.99}$ for the advancing and retreating blade sides with experimental data from transducers and the PSP technique^{(Reference Wong, Watkins, Goodman, Crafton, Forlines, Goss, Gregory and Juliano10)}. (a) Advancing blade side. (b) Retreating blade side.

The CFD data agrees very well with the data from the pressure transducers. Excellent agreement is seen on the retreating blade side, whereas on the advancing side, the surface pressure is slightly overpredicted. The pressure transducers, do not however, resolve the suction peak, hence this key feature of the pressure distributions cannot be verified. The pressure sensitive paint data fails to capture the correct curve trends, which is especially visible on the retreating blade side, where the dynamic pressure is low. Some errors may occur due to the fact that the pressure using the PSP technique was extracted at $r/R=0.982$, whereas the pressure transducers were installed at $r/R=0.99$. However, based on the CFD predictions the differences between these two radial stations are small. Unfortunately, further experimental data for the PSP rotor blade in forward flight is unavailable.

6.0 ROTOR DESIGN COMPARISON

6.1 Performance metrics

The typically used performance metrics are analysed first, in terms of their usage when comparing different rotor designs at a specific design point. In hover, the key efficiency parameter is the figure of merit which relates the ideal power from momentum theory with the actual power required. The figure of merit is written in terms of dimensional units in Equation 2.

(2)\begin{equation}FoM = \frac{C_T^{3/2}}{\sqrt{2} C_Q} = \frac{T \sqrt{\rm DL} }{P\sqrt{2\rho}}\end{equation}

where, DL (= T/A) is the rotor disk loading, T is the rotor thrust, P is the rotor power and A is the disk area.

Based on Equation 2, rotors with a higher disk loading will achieve higher values of FoM due to the 3/2 power factor of the thrust coefficient. However, for high rotor efficiency, high power loading (defined as weight/power ratio) is sought for, and is maximised by minimizing disk loading and maximising FoM. The disk loading value, however, is usually set based on the vehicle class and sizing requirements. Rotors at high disk loading will be driven to higher values of FoM, due to a higher ratio between induced and profile power, as shown by Prouty^{(Reference Prouty25)}. Furthermore, a higher solidity (geometric) rotor will lead to a shift in the maximum FoM value to higher thrust coefficients by delaying the onset of stall. For this reason, the solidity (in many cases thrust-weighted) of a rotor is constrained in many hover optimisation studies^{(Reference Leon, Le Pape, Desideri, Alfano and Costes7-Reference Imiela9,Reference Le Pape and Beaumier26)} , when the objective is to maximise the FoM. This can be avoided by reformulating the objective as a power minimisation problem at constant thrust. The power required at a specific weight is more important in real-life rotor design than the FoM value. To compare the different rotor designs, the net thrust values are given in Table 5. The values are based on CFD results, and hence account for the planform shape as well as solidity effects. The scaled values assume a constant chord length among the three rotor blade designs, giving similar conclusions as seen in Section 3, Blade Geometries. The PSP rotor blade, which was tested experimentally, delivers a higher net thrust compared to the Langley blades, due to the higher rotor radius. However, when scaled to the rotor radius of the Langley blades (1.428m), the PSP rotor delivers a much lower net thrust, primarily due to the lower tip speed. The LBL blade design delivers a higher net thrust than the LBERP blade due to higher geometric solidity (larger chord length). As shown here, rotors at the same thrust coefficient can be operating at different net thrusts, due to different chord length and planform geometry. Nevertheless, the main reason for the higher FoM for the PSP rotor when compared to the Langley blade designs, comes from reduced compressibility effects due to the lower blade tip Mach number (0.58 compared to 0.628). For rotors operating at the same net thrust, higher FoM values are obtained at lower blade tip Mach number (the lower limit of the blade tip Mach number is constrained by forward flight design considerations). Based on the interplay of many design parameters, the use of the FoM metric alone has its limitations when comparing different rotors for a particular design point, operating at different disk loadings, tip Mach numbers and net thrust values. For similar planforms and for similar disk areas, the FoM comparison makes more sense.

Table 5 Net thrust values for the three rotor blade designs at $\textit{C}_{\textit{T}}=\text{0.008}$ based on the scaled blades (scaled by a unit chord) used within the CFD simulations, the experimental values and values scaled to an equal rotor radius

In forward flight, the aerodynamic efficiency measure often used is the lift to drag ratio (L/D), shown in Equation 3.

(3)\begin{align}\frac{L}{D} = \frac{W V_\infty}{P} = \frac{C_L}{C_Q} \mu\\[-18pt]\nonumber\end{align}

where W is the weight of the helicopter, $V_\infty$ is the flight speed and P is the rotor power, and $\mu$ is the rotor advance ratio.

In rotorcraft, this parameter is proportional to the power loading and flight speed of the helicopter. Rotors with high disk loading will generally have a lower power loading, and hence lower lift to drag ratio. Therefore, this parameter will favour rotor designs with low disk loading. The lift to drag ratio will decrease with increasing weight of the helicopter. Heavy-lift helicopters will generally have poor lift to drag ratios, however, may have a much wider flight envelope in terms of payload than lower loaded helicopters. Direct comparison of rotor designs in terms of lift to drag ratio is only valid for rotors with the same disk loading, as well as aircraft weight. Furthermore, this parameter does not directly account for differences in the generated propulsive force. For this reason, an equivalent lift to drag ratio, $(L/D)_e$, is also often used, defined in Equation 4.

(4)\begin{align}\left( \frac{L}{D} \right)_e = \frac{C_L}{C_Q/\mu - C_D}\\[-18pt]\nonumber\end{align}

where $C_D$ is the drag coefficient which is equal to the propulsive force coefficient (assumed trim).

The calculated lift to drag ratios, as well as equivalent lift-to-drag ratios when scaled to two different full-scale helicopter rotors (UH-60A and AH-64) are shown in Table 6. This is done to demonstrate the $L/D_e$ metric for full-scale rotors.

Table 6 Comparison of various lift-to-drag ratio values for the LBERP, LBL and PSP rotor designs at $\textit{C}_{\textit{T}}=\text{0.0081}$ and $\mu=\text{0.4}$. Same propulsive force coefficient assumed for the AH-64 and UH-60A helicopters

At a constant thrust coefficient of $0.0081$, the PSP rotor blade generates 20% less net thrust than the Langley blades (scaled to the same rotor radius), primarily due to the lower blade tip Mach number. This leads to higher L/D ratio of the PSP rotor compared to the Langley blades. The equivalent lift to drag ratios are calculated by scaling the model-scale rotor blades to full-scale radius. The drag coefficient is calculated based on the prescribed shaft angle. Therefore, the propulsive force generated by the PSP rotor blade is lower than for the LBL and LBERP designs. The propulsive force required for the UH-60A and AH-64A helicopters was assumed as constant (although the equivalent flat plate areas will not be due to different rotor radii). The equivalent lift to drag ratio is the same for any helicopter as the value is only dependent on the rotor lift and torque and the required propulsive force. However, the Apache helicopter is operated at a higher disk loading, and hence for a given thrust coefficient, the weight of the aircraft will be lower. Here, at $C_T=0.0081$, the UH-60A operates at 22,132lbs whereas the Apache rotor operates at 18,362lbs. In fact, the condition of $C_T=0.0081$ and $\mu=0.4$ is outside the flight envelopes of both helicopters. Based on these observations it can be stated, that the L/D and $(L/D)_e$ values may be misleading for different rotor designs. The rotors must be compared for the same helicopter weight and disk loading to gain valuable insight.

Based on the analysis of figure of merit and lift-to-drag ratio, care must be taken when comparing rotors that come from different helicopters, due to different blade tip Mach numbers, disk loadings and net thrusts at a constant thrust coefficient. For this reason, when comparing rotors operating at different conditions, moving to the dimensional form of forces and moments may be more valuable. In optimisation studies, however, when the blade has a constant disk loading, radius and blade tip Mach number the figure of merit and lift-to-drag ratio parameters can be used as long as the objective function is correctly formulated.

6.2 Solidity effects

The effects of rotor solidity matching, are examined for the LBERP and LBL blade designs. The blades tested by Yeager et al^{(Reference Yeager, Noonan, Singleton, Wilbur and Mirick6)} were matched based on thrust-weighted solidity. Here, an additional, scaled LBL blade is simulated to match the nominal solidity of the LBERP blade. This study is aimed at investigating the findings of Perry^{(Reference Perry5)} who claimed that the definition of thrust weighted solidity is misleading. The solidity values for each of the blade designs was presented in the blade geometries section in Table 1. Firstly, the effect on the hover performance is examined. The hover predictions are shown in Fig. 6, based on thrust coefficient and blade loading ($C_T/\sigma_G$). For clarity, the experimental measurements are removed.

Figure 6. Effects of rotor solidity matching (nominal vs thrust-weighted) on the hover performance of the LBERP and LBL blades based on thrust coefficient and blade loading. (a) FoM vs $\textit{C}_{\textit{T}}$. (b) FoM vs $\textit{C}_{\textit{T}}/\sigma_{\textit{G}}$.

The hover performance results indicate a performance loss at high thrust coefficients for the LBLs blade when compared to the nominal LBL blade. A similar peak FoM is obtained with a much sharper performance deterioration with increasing thrust. The LBLs blade has equal performance to the LBERP blade at a lower thrust coefficient when comparing with the LBL blade. When the FoM is based on blade loading the LBLs curve is slightly shifted with respect to the LBL curve as the geometric solidity of the LBLs blade is now lower than the LBERP blade. This leads to equal performance of the LBERP and LBLs blade at a slightly higher collective, hence the sharp drop in FoM is slightly delayed. To examine the cause behind this behaviour of the performance curves, the surface pressure skin friction coefficient distributions along with skin friction lines at $13.5^\circ$ collective are investigated for the LBL and LBLs blade, shown in Fig. 7.

Figure 7. Surface pressure coefficient and skin friction distributions with skin friction lines near the blade tip for the LBL and LBLs blades at high thrust ($\text{13.5}^\circ$ collective). (a) $\textit{C}_{\textit{P}}$, LBL blade. (b) $\textit{C}_{\textit{P}}$, LBLs blade. (c) $\textit{C}_{\textit{F}}$, LBL blade. (d) $\textit{C}_{\textit{F}}$, LBLs blade.

As can be seen from Fig. 7, a stronger suction peak is seen inboards of the aerofoil transition as well as near the blade tip for the LBLs blade when compared to the LBL blade. This is due to the fact, that the load is distributed across a shorter chord leading to a sharper adverse pressure gradient. The pressure recovery at the trailing edge is also weaker indicating stronger stall for the LBLs blade. This also indicates that the LBLs blade will first encounter stall at a lower collective angle. The LBLs blade therefore, has poorer performance than the LBL blade showing the effect of rotor solidity on the stall boundary.

Solidity effects are also examined in high-speed forward flight ($C_T=0.0081,\mu=0.4$), with integrated loads shown in Table 7.

Table 7 Solidity effects on the rotor forward flight performance at high-speed, $\textit{C}_{\textit{T}}=\text{0.0081}, \mu =\text{0.4}$

Based on Table 7 the baseline LBL blade is slightly worse than the LBERP blade in terms of torque coefficient as predicted by the experiments. At the same trim state, the LBLs blade does not deliver the required thrust coefficient. This is not surprising due to the shorter chord of the blade and lower geometric solidity. After trimming to the required thrust coefficient the LBLs blade is worse than the LBERP blade. Here, a more extreme trim state is needed to attain the required thrust, with increased collective and longitudinal cyclic angles. On the retreating blade side, the blade pitch angle is increased by 1.51 degrees, leading to significantly higher power requirements, and hence worse performance compared to the LBERP design. This is confirmed by examining the skin friction lines shown in Fig. 8 (to highlight flow separation).

Figure 8. Retreating side skin friction lines and skin friction coefficient distributions for the nominal and scaled LBL rotor blades. (a) Nominal LBL blade. (b) Scaled LBL blade.

A significantly higher separation region can be seen for the scaled LBL blade, especially at 240–260$^\circ$ azimuthal locations. The lower blade solidity promotes stall on the retreating side leading to an increase in power. This statement is consistent with the findings of Perry^{(Reference Perry5)}, who compared the flight envelopes of a tapered planform with a BERP planform. As seen by Perry^{(Reference Perry5)} the definition of thrust-weighted solidity can give misleading results and will promote planforms with lower area near the blade tip. In our case, the differences between the LBL and LBERP blades are not as drastic as those described by Perry (who compared a BERP with a tapered planform)^{(Reference Perry5)} due to a lower area mismatch between the two blades. However, the matching of thrust-weighted solidity still promotes the LBL blade as it delivers a higher thrust of 1.5% when compared to the LBERP blade, purely due to larger chord. The main reason for the use of thrust-weighted solidity is to account for the additional blade weight of a blade with additional area near the blade tip, as seen for a BERP design. However, as stated by Perry^{(Reference Perry5)} the weight increase is of second order due to the outer structure of the blade only being a light fairing. To generate the same thrust, the blade chord of the tapered blade would have to be increased by 7.5%^{(Reference Perry5)} which would incur much more significant weight penalties. Another aspect is that the success of the BERP rotor design did not only come from the planform but also due to the advanced aerofoils which were designed with the planform shape. The use of the same aerofoils on a rectangular and BERP-like planform as seen for the LBL and LBERP blades may promote one of the blades. Furthermore, the addition of anhedral can greatly improve the hover performance^{(Reference Brocklehurst and Barakos22)}, and hence is examined in Section 6.3.2, Study on anhedral effects.

6.3 Further design comparisons based on CFD results

6.3.1 Hover results and discussion

Based on the findings from the performance metrics and solidity effects, comparisons of the three blade designs at a constant thrust coefficient can only be made from a qualitative point of view due to the different net thrusts produced. Firstly, the hover solutions are examined at $C_T=0.008$ for the three blade designs, along with the high thrust cases (13.5 deg collective) for the LBERP and LBL blades. The surface pressure distributions and skin friction lines are shown in Figs. 9–10.

Figure 9. Surface pressure and skin friction coefficient distributions along with skin friction lines across the blade tip for the LBERP, LBL and PSP blade designs at $\textit{C}_{\textit{T}}$=0.008. (a) LBERP, $\textit{C}_{\textit{p}}$. (b) LBERP, $\textit{C}_{\textit{f}}$. (c) LBL, ${\textit{C}_{\textit{p}}}$. (d) LBL, $\textit{C}_{\textit{f}}$. (e) PSP, $\textit{C}_{\textit{p}}$. (f) PSP, $\textit{C}_{\textit{f}}$.

Figure 10. Surface pressure and skin friction coefficient distributions along with skin friction lines across the blade tip for the LBERP and LBL designs at 13.5 degrees collective. (a) LBERP, $\textit{C}_{\textit{p}}$. (b) LBERP, $\textit{C}_{\textit{f}}$. (c) LBL, $\textit{C}_{\textit{p}}$. (d) LBL, $\textit{C}_{\textit{f}}$.

The typical characteristics of the blade loading distribution across the blade tips for each blade design can be seen in the pressure coefficient distribution plots. For the LBERP tip, two regions of high suction exist, which are inboard of the notch and round the swept tip. With increasing collective these suction regions grow, propagate inboard and cover a larger portion of the paddle-shape tip. The effect of the tip vortex is also clearly seen. The tip vortex separates inboards of the very tip of the blade, which is especially visible for the high collective case, due to a reduced pressure recovery near the trailing edge. This could be one of the causes for the poor performance of the LBERP blade, as the blade tip vortex is expected to form round the curve tip. Such behaviour of the tip vortex can be seen for the production BERP III and BERP IV blades based on the surface pressure distributions in hover (Euler computation)^{(Reference Robinson and Brocklehurst21)}. The early vortex separation for the LBERP blade is potentially attributed to the too low blade thickness in this region. Tapering off the blade quadratically rather than linearly could potentially prevent this, leading to a more optimal blade thickness distribution. The high collective angle used here (13.5 degrees), may be out of the operational range of light/medium weight helicopter making the BERP-like design better suited for heavy-lift applications. The pressure distribution for the LBL blade is typical of a rectangular blade design. A sharp suction peak can be seen near the leading edge at the tip of the blade which leads to decreased performance compared to more modern blade designs such as a design with a parabolic blade tip. The rapid aerofoil transition, causes a non-smooth pressure distribution, which can especially be seen in Fig. 9c). At the higher collective the pressure contours indicate the onset of separation across the blade tip, as the blade pressure is no longer recovered at the trailing edge. The PSP blade pressure contours, show the effect of sweeping the blade tip. A reduced suction is seen when compared to the rectangular blade, with the sweep onset acting as a aerodynamic discontinuity. The more favourable pressure contours, however, are also due to the lower blade tip Mach number.

Further observations can be made based on the skin friction lines. For the LBERP blade, the skin friction lines at the very tip of the blade indicate the presence of the tip vortex. The tip vortex forms further inboard than for a typical BERP blade^{(Reference Robinson and Brocklehurst21)}, as seen in the pressure distribution contours. At the higher thrust case, the vortex forms even further inboards. A different thickness distribution as well as leading edge curve outboard of 0.95R could potentially improve these surface streamline flow features, leading to formation of the tip vortex round the curved blade tip. Evidence of the notch vortex formation is also seen for the higher thrust case, as a drop in skin friction is seen. At higher thrust, a low level of shock induced separation can be observed near the leading edge. The skin friction lines indicate much stronger separation for the LBL blade at high thrust. Significant separation is seen across the blade tip, with a weak separation also seen at $C_T=0.008$, indicated by a near zero skin friction and non-smooth skin friction line distribution. These features are highlighted in Figs. 9–10. At high thrust, the pressure is no longer fully recovered at the trailing edge for the LBL blade, indicating the onset of stall. This is the primary reason for the lower performance of this blade at 13.5 degrees collective when compared to the LBERP design, which is able to operate at much higher collectives without developing stall. The flow over the tip of the PSP rotor blade is much cleaner as no shock induced separation is observed, which is also due to the lower blade tip Mach number, as stated previously. Unfortunately, a high collective case is unavailable for the PSP rotor blade for comparisons at high thrust.

The chordwise surface pressure coefficients are examined further for the three blade designs at r/R = 0.95 and shown in Fig. 11. The critical pressure coefficients are also shown to indicate where the flow becomes supersonic.

Figure 11. Chordwise surface pressure coefficient at r/R = 0.95 for the LBERP, LBL and PSP blade designs. (a) $\textit{C}_{\textit{T}}\,\text{=}\,\text{0.008}$. (b) 13.5 deg collective (high thrust)

The chordwise pressure coefficient distributions show that the comparison of different blade designs at a constant radial station is not fully valid. The key features of the blade pressure distribution are dependent on the planform shape, and may be located at different radial stations. For example at r/R = 0.95, a drop in the suction peak is observed for the PSP rotor blade, as this is the point of the sweep initiation. A region of higher suction is seen for the LBERP blade further inboard (r/R = 0.82) due to the notch geometry, which is not present for the straight PSP rotor blade. However, qualitative observations can be made based on the chordwise surface pressure at $r/R = 0.95$. At $C_T=0.008$ it can be seen that the suction peak for the LBL blade is much higher than for the other two blades. This is due to sweep incorporated in the LBERP design (as well as slightly lower collective and larger local chord). The LBERP blade has a sweep of only 9 degrees, however the blade loading is also distributed over a larger area due to the increased blade chord. These are also the reasons for reduced chordwise extent of supersonic flow when compared to the LBL blade. The flow over the PSP rotor blade at $r/R = 0.95$ is subsonic, as the suction peak is below the critical surface pressure coefficient. This is due to the lower blade tip Mach number when compared to the Langley blades. For the cases at 13.5 degrees collective, a similar suction peak magnitude can be observed for the LBL and LBERP blades. However, at this collective, the LBERP blade operates at a much higher thrust coefficient. Once again, the supersonic flow region is reduced for the LBERP blade, when compared to the LBL blade. The pressure is no longer fully recovered for the LBL blade, indicating the onset of stall.

The analysis of different blade designs is continued by extracting the sectional blade loads for the three blade designs at $C_T=0.008$, shown in Fig. 12. The LBL loads are also shown scaled to the radius of the LBERP blade (1.09 factor). The loads are scaled by the local flow velocity and reference blade chord equal to the chord of the first aerodynamic blade section.

Figure 12. Sectional thrust and torque distributions for the LBERP, LBL and PSP blade designs at $\textit{C}_{\textit{T}}\,\text{=}\,\text{0.008}$. Loads are scaled by the local flow velocity and reference blade chord equal to the chord of the first aerodynamic section. (a) $\textit{C}_{\textit{t}}$. (b) $\textit{C}_{\textit{q}}$.

The sectional thrust distributions indicate a similar blade loading for the three blade designs. Due to the scaling by local flow velocity, the loading at the root of the blade is augmented. The two peaks in the blade loading are due to the formation of the tip vortex as well as the effect of the preceding blade tip vortex. The loading peak at the blade tip is higher for the LBERP blade when compared to the LBL blade, leading to reduced hover performance. This is potentially due to the non-optimal thickness distribution across the tip of the blade. The PSP rotor blade has a much more optimal loading distribution compared to the Langley blades. However, this is also due to the higher blade twist of the blade (14 degrees compared to 9 degrees), as can be seen by the slope of the blade loading distribution curve. This leads to an offloading of the blade tip, and hence higher performance. The radial torque distributions show much greater differences. The LBERP blade geometry leads to a reduction in local torque at the notch, however, an increased torque is observed across the paddle type blade tip. A reduced peak is seen at the blade tip when compared to the LBL blade. The result of the aerofoil transition can also be seen for the LBL blade. A more uniformly distributed loading can once again be seen for the PSP blade. In particular, the swept blade tip leads to a significant drop in local torque.

The tip vortex formations are examined next for the three blade designs and are shown in Fig. 13.

Figure 13. Vortex formation for the LBERP, LBL and PSP blade designs at $\textit{C}_{\textit{T}}\,\text{=}\,\text{0.008}$ based on contours of vorticity. (a) LBERP. (b) LBL. (c) PSP.

For the LBERP blade, the onset of the tip vortex is located close to the edge of the blade tip, further inboards than for the other two blade designs. The tip vortex grows around the curved tip, moving towards the upper surface near the trailing edge of the blade. A typical vortex pair is formed from the lower and upper surfaces of the rotor blade. A secondary tip vortex structure (from the lower surface) is present in the main vortex core for a longer period for the LBERP blade compared to the other two blades. For the PSP and LBL blades, both blade tip vortices form on the upper surface close to the blade leading edge. The tip vortex for the PSP blade, however, travels a shorter distance before separating at the blade trailing edge due to the blade tip taper (shorter distance between leading and trailing edge). The blade sweep also moves the vortex onset downstream along the chordwise direction. These features can have a significant effect on the loading at the blade tip and hence the rotor blade performance.

6.3.2 Study on anhedral effects

Another solution for improving hover performance is blade anhedral. Anhedral effects were studied for the LBERP and LBL blades at 10.5 degrees collective, through applying 15 degrees parabolic anhedral initiated at 0.945R (the starting position of the LBERP raked tip). The performance improvement is shown in Table 8.

Table 8 Hover performance of standard LBERP and LBL blades, and blades with 15 degrees parabolic anhedral

The tip anhedral increases the hover performance for both blades. For the LBL blade, a performance improvement of approximately three counts in FoM is achieved, whereas the LBERP blade sees an increase of over four counts. Therefore, it can be stated that blade anhedral is more beneficial for the LBERP geometry than the LBL blade. This is due to the fact that anhedral generally benefits highly loaded rotor blades, and the BERP-like geometry genereates a stronger downwash field in the blade tip region compared to a rectangular blade. Similar observations were made by Brocklehurst and Barakos^{(Reference Brocklehurst and Barakos22)} in their review of helicopter blade tip shapes. The LBERP blade with 15 degrees achieved a similar FoM as for the standard LBL blade. The performance improvement due to anhedral, comes from a small increase in thrust and torque reduction. No experimental data exists to validate this results, however the benefit of blade anhedral is also seen for the S-76 rotor blade^{(Reference Balch and Lombardi27)}. To examine the sources of the beneficial action of anhedral, the surface pressure distributions and sectional loads are compared. The surface pressure distribution for the LBERP and LBL blades with and without anhedral are shown in Fig. 14. The pressure coefficient is normalised by local flow velocity.

Figure 14. Comparison of the surface pressure distributions (normalised by local flow velocity) for the LBL and LBERP blades in hover with and without anhedral. (a) LBL blade. (b) LBL blade with 15 deg anhedral. (c) LBERP blade. (d) LBERP blade with 15 deg anhedral.

The anhedral is found to redistribute the loading along the blade leading to an offloading of the blade tip and higher loading inboard. This leads to a more optimal induced lift distribution and reduced overall torque. In fact, the blade anhedral acts similarly as an additional negative twist on the blade loading distribution. The differences in blade loading for the blades with and without anhedral are noticeably lower for the LBL blade. The aerofoil transition region, can also be clearly seen in the surface pressure distributions, where the pressure iso-lines spread out. For the LBERP blade, a reduced suction at the blade tip can be observed (caused by formation of the tip vortex). The suction, however, is increased in the blade notch region. This is highlighted further through the sectional load distributions, in Fig. 15. The loads are normalised by local flow velocity and the reference blade chord taken as the chord of the first aerodynamic section.

Figure 15. Comparison of sectional thrust and torque distributions for the LBL and LBERP blades in hover with and without anhedral. (a) LBL blade, $\textit{C}_{\textit{t}}$. (b) LBL blade, $\textit{C}_{\textit{q}}$. (c) LBERP blade, $\textit{C}_{\textit{t}}$. (d) LBERP blade, $\textit{C}_{\textit{q}}$.

The observations from the surface pressure distributions are confirmed by the sectional load distributions. The anhedral has a similar effect on the rotor thrust distributions, where a larger amount of thrust is generated inboard. The benefit of anhedral, mainly comes from a reduction in torque at the blade tip, which is seen for both blades. For the LBERP tip, the largest reduction can be seen across the paddle-like blade tip, as well as at the very end of the tip where the tip vortex forms. For the LBL blade, the torque is reduced past the aerofoil transition region.

To investigate the differences in blade loading, the vertical tip vortex displacements are extracted from the solutions and are shown in Fig. 16.

Figure 16. Comparison of the tip vertical vortex displacements for the LBL and LBERP blades in hover with and without anhedral.

Figure 17. Comparison of vortex strength for the Langley blades with and without anhedral as indicated by a Q-criterion contour at various azimuthal locations. A cutoff below Q = 0.02 is applied. (a) LBL blade. (b) LBL blade with anhedral. (c) LBERP blade. (d) LBERP blade with anhedral.

Figure 18. Rotor disk plane load distributions for LBERP, LBL and PSP blades at 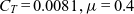$\textit{C}_{\textit{T}}\,\text{=}\,\text{0.0081}, \mu\,\text{=}\,\text{0.4}$. All loads are scaled by the reference blade chord, equal to the chord of the first aerodynamic section. (a) LBERP, $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$. (b) LBERP, $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$. (c) LBERP, $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$. (d) LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$. (e) LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$. (f) LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$. (g) PSP, $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$. (h) PSP, $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$. (i) PSP, $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$. (j) LBERP-LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$. (k) LBERP-LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$. (l) LBERP-LBL, $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$.

The vertical tip vortex displacements indicate that for the blades with anhedral, so called “vortex snaking” occurs, as the tip vortex initially moves upwards back towards the rotor disk in the initial wake ages before displacing downwards. This is due to the formation of much weaker tip vortices when compared to blades without anhedral. This behaviour was also observed by Brocklehurst and Barakos^{(Reference Brocklehurst and Barakos22)}. The typical change in the gradient of vortex descent is seen as the vortex passes the next blade at 90 degrees azimuth. The vertical miss distance is marginally higher for the blades with anhedral, however this effect is not seen to be significant. In the later wake ages, the vortex displacement is similar for all blades, except for the LBL blade without anhedral which displaces at a slower rate. At this collective, the LBL blade produces a weaker downwash field near the blade tip compared to the LBERP blade. This also leads to a reduced effect on the tip vortex vertical displacements due to the introduction of anhedral. The vortex strength due to the introduction of anhedral is examined next, and is shown in Fig. 17.

For both blade designs, the addition of anhedral leads to a weaker tip vortex. The rotor blades were not trimmed to the same thrust coefficient, however, the values in Table 8 indicate a minor increase in thrust with the addition of anhedral. The LBERP blade generates a weaker blade tip vortex at this collective, despite operating at a higher thrust coefficient. The vortex radius before interacting with the next blade is also clearly larger for the LBERP blade when compared to the LBL blade. Based on these observations, it can be seen that the LBERP tip vortex aerodynamics are favourable compared to the LBL blade, due to reduced interaction of the blade with the preceding blade tip vortices, leading to reduced induced power and acoustic signature. The addition of anhedral further offloads the blade tip. The effects of anhedral also show that advanced planforms require careful computational optimisation. This is due to the strong sensitivity of the blade performance on geometric features such as anhedral, as shown for the LBL and LBERP blades.

6.3.3 Forward flight results and discussion

Further analysis is performed by examining the LBERP, LBL and PSP blades in high-speed forward flight. The three blades were simulated at the same advance ratio of 0.4 and trimmed to the same thrust coefficient of 0.0081 (whilst minimising pitching and rolling moments). The obtained trim states are shown in Table 9.

Table 9 Trim states for the forward flight computations of the LBERP, LBL and PSP blades at $\mu=0.4$ and $C_T=0.0081$. All values given in degrees

Figure 19. Azimuthal blade loads for the LBERP and LBL blades. Loads are normalised by the reference blade chord (chord of the first aerodynamic section). (a) $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$, $\textit{r/R}\,\text{=}\,\text{0.75}$. (b) $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$, $\textit{r/R}\,\text{=}\,\text{0.9}$. (c) $\textit{M}^{\text{2}}\textit{C}_{\textit{N}}$, $\textit{r/R}\,\text{=}\,\text{0.975}$. (d) $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$, $\textit{r/R}\,\text{=}\,\text{0.75}$. (e) $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$, $\textit{r/R}\,\text{=}\,\text{0.9}$. (f) $\textit{M}^{\text{2}}\textit{C}_{\textit{M}}$, $\textit{r/R}\,\text{=}\,\text{0.975}$. (g) $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$, $\textit{r/R}\,\text{=}\,\text{0.75}$. (h) $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$, $\textit{r/R}\,\text{=}\,\text{0.9}$. (i) $\textit{M}^{\text{2}}\textit{C}_{\textit{C}}$, $\textit{r/R}\,\text{=}\,\text{0.975}$.

The trim states, indicate a lower collective and longitudinal cyclic angles for the PSP rotor blade when compared to the Langley blades. This is due to the fact that this rotor produces a lower net thrust for a given thrust coefficient (due to a lower blade tip Mach number). The matching of thrust-weighted solidity, which led to an increase in 9% chord for the LBL blade, leads to a slightly lower collective and longitudinal cyclic compared to the LBERP blade. The shaft, flapping and coning angles are prescribed.

The rotor disk blade loads are extracted for the three blade designs and shown in Fig. 10. Note that the PSP blade loads are shown on a different scale compared to the Langley blades. As the LBL and LBERP blades were simulated at the same blade tip Mach number, the difference between these two blades is also shown. All loads are scaled by the reference blade chord (equal to the chord of the first aerodynamic section), and the pitching moments are taken about the local quarter chord location (chord taken as normal to pitch axis).

Figure 18 indicates fairly similar load distributions for the three blade designs. Unfortunately, the loads from the PSP case, cannot be compared quantitavely with the Langley blades due to the lower blade tip Mach number. However, qualitatively, the normal force distributions indicate that the main lifting regions are the front and back of the rotor disk. The LBERP blade, provides a higher normal force at the front of the rotor disk and on the retreating blade, when compared to the LBL blade, which is not surprising due to the tip shape (larger chord). On the advancing blade a slightly larger region of negative thrust can be seen. The extent of this region is significantly increased for the PSP rotor blade. This is predominantly, due to the higher twist of this rotor blade, leading to operation of the local aerofoil section in this region at higher negative angles of incidence. The moment distributions indicate a positive, nose-up pitching moment as the blade moves from the back of the disk to the advancing side and a nose-down negative pitching moment as the blade moves from the advancing side to front of the disk. The LBERP blade exhibits much larger pitching moments compared to the simpler LBL and PSP planforms. In particular, the moments indicate, blade structural untwisting across the blade tip at the advancing side and increased twisting on the retreating side. This could have positive effects on the rotor performance, however, as the blade is modelled as rigid, structural deformations are not taken into account. Regarding the chordwise force distribution, for all three rotor blades, the high regions of torque are at the front and back of the rotor disk as well as the retreating side. On the advancing side, the notch feature of the LBERP planform and the initiation of the sweep for the PSP rotor blade, lead to a negative chordwise force. A similar effect is seen for the LBL blade, in the position of the aerofoil transition region to a lesser degree. The LBERP blade produces a significantly higher chordwise force inboards of the blade tip compared to the LBL blade. This is due to the higher loading close to the notch feature of the LBERP planform. Significant variations can be seen across the blade tip which generally follow the pitching moment distributions. A nose-up pitching moment generally leads to an increase in the local chordwise force. Based on the blade load distributions, it can be stated, that aeroelastic deflections will be important for simulation of advanced planforms, as a much larger variation of pitching moments is seen across the rotor blade tip, leading to much more significant elastic blade twist deformations. The blade loads are compared quantitavely for the LBL and LBERP blades, by extracting the azimuthal loads at $r/R = 0.75, 0.9$ and $0.975$ which is shown in Fig. 19.

As expected, at the $r/R=0.75$ radial station, the loads for the LBERP and LBL blades are very similar, as the shape of the planform and aerofoil sections are the same. The effect of the notch can be seen at this station in the slightly higher normal and chordwise forces at the front and back of the rotor disk. At the $r/R=0.9$ radial station, the LBERP blade starts to lift more at the back of the disk at the expense of high nose-down pitching moment on the advancing blade side and higher torque on the retreating blade side. A higher chordwise force is also encountered on the retreating blade. At $r/R=0.975$ the LBERP blade obtains a much higher normal force as can be seen at the back of the disk, however, on the retreating side a loss of lift is encountered leading to a normal force and chordwise force reduction at the front of the disk. A certain level of oscillations exists in the pitching moment curve at $r/R = 0.975$ for the LBERP blade.

The advancing and retreating blade sides are now examined in more detail for all three blade designs. The surface pressure coefficient distributions at $90^\circ$ azimuth along with the flow field streamlines and Mach number contours at $r/R = 0.82$ can be seen in Fig. 20.

Figure 20. Advancing side pressure distributions and flow field streamlines along with contours of Mach number at $\text{r/R}\,\text{=}\,\text{0.82}$ for the LBERP, LBL and PSP rotor blades at $\mu\,\text{=}\,\text{0.4},\textit{C}_{\textit{T}}\,\text{=}\,\text{0.0081}$. (a) LBERP, $\textit{C}_{\textit{P}}$ distribution. (b) LBERP, Mach contours. (c) LBL, $\textit{C}_{\textit{P}}$ distribution. (d) LBL, Mach contours. (e) LBL, $\textit{C}_{\textit{P}}$ distribution. (f) LBL, Mach contours.

The surface pressure solutions on the advancing blades indicate strong shocks for both LBERP and LBL blades. The notch geometry prevents the shock from propagating onto the tip surface through a reduction in the thickness to chord ratio. However, it can be seen that for the rectangular LBL blade, the shock also stops at a similar radial location. This is the position of the aerofoil transition ($r/R=0.84$–$r/R=0.866$). Another geometric design feature that may have a significant effect on the dissipation of the shock is the sudden change in the gradient of the blade twist curve. The twist is constant across both the LBL and LBERP blade tips, which generates an aerodynamic discontinuity at $r/R = 0.866$. Based on these observations, it is not surprising that both blades show similar values of normal and chordwise forces on the advancing blade side. The strong nose-down pitching moment for the LBERP blade, however, could give rise to significant pitch-link loads. The addition of blade anhedral could potentially reduce these strong pitching moment variations, due to reduced loading at the blade tip. The PSP blade surface pressure distribution indicates, that the region of high suction is reduced more gradually, as a shock does not form. This is expected due to the lower blade tip Mach number compared to the other two blades. The Mach number contours, show a larger chordwise extent of supersonic flow for the LBERP blade compared to the LBL design. The primary reason for this is associated with the stronger downwash field near the blade tip for the LBERP blade. A weaker shock also forms on the blade lower surface for both Langley blade designs. No evidence of shock-induced separation is seen on the blade upper surface for either blade design, with a small recirculation bubble present on the blade lower surface for the LBL and LBERP blades. The $C_L$ values are close to zero for both blades due to the low local incidence of the aerofoil section. The PSP Mach contours only indicate the presence of the compression on both upper and lower surface, without the presence of a distinct shockwave, which is due to the lower blade tip Mach number. The retreating side flow physics are also examined in more detail. The surface pressure and skin friction coefficient distributions along with skin friction lines near the blade tip are shown in Fig. 21.

Figure 21. Retreating side pressure and skin friction distributions along with skin friction lines for the LBERP, LBL and PSP rotor blades. (a) LBERP, $\textit{C}_{\textit{p}}$. (b) LBERP, $\textit{C}_{\textit{f}}$. (c) LBL, $\textit{C}_{\textit{p}}$. (d) LBL, $\textit{C}_{\textit{f}}$. (e) PSP, $\textit{C}_{\textit{p}}$. (f) PSP, $\textit{C}_{\textit{f}}$.

No evidence of dynamic stall was found for any of the blade designs in the high-speed forward flight condition. The loading distribution and skin friction lines on the retreating side for the LBERP blade indicate the presence of a notch vortex (highlighted with red boxes), which prevents propagation of separated flow to the blade tip. Due to the moderate thrust coefficient, no significant separation is seen inboard of the notch and as expected the flow over the blade tip remains attached. At the very tip of the LBERP blade, changes can be seen in both the pressure distributions and skin friction lines. The tip vortex rolls up on the upper surface of the blade inboards of the very tip of the blade up to the $270^\circ$ azimuthal location. After passing the retreating side, a drop in skin friction can be observed, along with the skin friction lines oriented in a more spanwise direction. Here, the tip vortex rolls up around the curved blade tip and detaches further outboard. Once again, the thickness distribution across the very blade tip of this geometry could potentially have a significant effect on the flow physics in this region. The surface pressure distributions for the LBL blade shows a distinct drop in the suction pressure in the aerofoil transition region. As indicated by the skin friction lines, a separation bubble is present near the leading edge of the blade. The chordwise extent of this separation, however, is not very large, hence not leading to a drastic increase in the rotor power. While the steep reduction in aerofoil thickness and discontinuity in the blade twist led to promising features for the LBL blade on the advancing blade side, adverse flow features were found on the retreating side. However, these features would have a much more significant effect, if the LBL blade was simulated at the same geometric solidity as the LBERP blade, leading to more severe retreating side separation, and potentially dynamic stall. No flow features of major significance, can be seen for the PSP rotor blade design showing that this rotor does not suffer from poor retreating blade performance due to the low blade tip Mach number. At a higher thrust level (or matched net thrust), however, this blade may stall more abruptly compared to the Langley blade designs due to lower blade tip area and lower tip speed.