We introduce a multivariate class of distributions with support I, a k-orthotope in 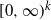$[0,\infty)^{k}$ , which is dense in the set of all k-dimensional distributions with support I. We call this new class ‘multivariate finite-support phase-type distributions’ (MFSPH). Though we generally define MFSPH distributions on any finite k-orthotope in $[0,\infty)^{k}$ , here we mainly deal with MFSPH distributions with support 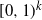$[0,1)^{k}$ . The distribution function of an MFSPH variate is computed by using that of a variate in the MPH $^{*} $ class, the multivariate class of distributions introduced by Kulkarni (1989). The marginal distributions of MFSPH variates are found as FSPH distributions, the class studied by Ramaswami and Viswanath (2014). Some properties, including the mixture property, of MFSPH distributions are established. Estimates of the parameters of a particular class of bivariate finite-support phase-type distributions are found by using the expectation-maximization algorithm. Simulated samples are used to demonstrate how this class could be used as approximations for bivariate finite-support distributions.