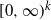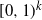1. Introduction
A phase-type (PH) distribution, introduced by [Reference Neuts7], is the distribution of the time until absorption in a finite-state Markov chain with exactly one absorbing state into which absorption is certain. Its denseness (in a weak convergence sense) in the set of all distributions with support
![]() $ [0,\infty) $
and its usefulness in applied probability make it an important family of distributions. Reference [Reference Assaf, Langberg, Savits and Shaked3] extended the PH variate concept to a multidimensional setup by introducing a finite number of sets of absorbing states. They called the resulting class ‘multivariate phase-type distributions’ (denoted by MPH) and studied its properties. Later, [Reference Kulkarni6] introduced a different class of multivariate phase-type distributions (denoted by MPH*) based on the total accumulated reward until absorption in a finite-state, continuous-time Markov chain, and showed that it is a strict superset of the MPH class. Both the MPH and MPH* classes with support
$ [0,\infty) $
and its usefulness in applied probability make it an important family of distributions. Reference [Reference Assaf, Langberg, Savits and Shaked3] extended the PH variate concept to a multidimensional setup by introducing a finite number of sets of absorbing states. They called the resulting class ‘multivariate phase-type distributions’ (denoted by MPH) and studied its properties. Later, [Reference Kulkarni6] introduced a different class of multivariate phase-type distributions (denoted by MPH*) based on the total accumulated reward until absorption in a finite-state, continuous-time Markov chain, and showed that it is a strict superset of the MPH class. Both the MPH and MPH* classes with support
![]() $ [0,\infty)^{k} $
are dense in the set of all distributions with support
$ [0,\infty)^{k} $
are dense in the set of all distributions with support
![]() $ [0,\infty)^{k} $
. A natural question that arises is whether, if we consider a k-orthotope I in
$ [0,\infty)^{k} $
. A natural question that arises is whether, if we consider a k-orthotope I in
![]() $[0,\infty)^{k}$
, there exists a class of distributions which is dense in the set of all distributions with support I. In the one-dimensional case, one such class was derived from the PH class in [Reference Ramaswami and Viswanath8], known as the finite-support phase-type (FSPH) class. Like the PH class, FSPH preserves both the denseness property and the underlying Markov chain structure. In this paper we introduce a similar concept in the multidimensional case by using the MPH* class. We derive a new class of distributions (denoted by MFSPH), with support on a finite orthotope I, which is dense in the set of all multivariate distributions with support I.
$[0,\infty)^{k}$
, there exists a class of distributions which is dense in the set of all distributions with support I. In the one-dimensional case, one such class was derived from the PH class in [Reference Ramaswami and Viswanath8], known as the finite-support phase-type (FSPH) class. Like the PH class, FSPH preserves both the denseness property and the underlying Markov chain structure. In this paper we introduce a similar concept in the multidimensional case by using the MPH* class. We derive a new class of distributions (denoted by MFSPH), with support on a finite orthotope I, which is dense in the set of all multivariate distributions with support I.
The need for new classes of distributions in the multidimensional case is well established in various areas like financial risk control theory, insurance theory, etc. In these areas, usually the multivariate distributions are constructed by using the concepts of copulas [Reference Cherubini, Luciano and Vecchiato4]. However, choosing the right copula for this purpose is itself a big task. Moreover, the idea behind the approach based on copulas is to match the marginals and the correlation. Sometimes, in practical situations, estimating the covariance matrix itself creates a computational burden. The denseness property of the MFSPH distribution enables us to use it as a substitute for the copula distributions. At the same time, the construction of the MFSPH variate preserves the Markov structure of the underlying process, and hence it is much easier to handle the distribution than other multivariate classes of distributions.
The organization of the rest of the paper is as follows. After some preliminaries in Section 2, we introduce a modified definition for the FSPH class in Section 3, which we use to define the MFSPH distribution. Being derived from the MPH* class, the MFSPH class also has a strong connection with Markov chains, which makes it more convenient to handle. Since no explicit form for the distribution function of an MPH* variate is available (see also [Reference Kulkarni6]), we are not able to express the distribution function of an MFSPH variate explicitly. However, we do establish a relation between the distribution functions of MFSPH and MPH* variates in Section 3. Apart from this, we study some properties of this new class in Section 3, and in Section 4 we estimate the parameters of a particular class of bivariate finite-support distribution using the expectation-maximization (EM) algorithm. A discussion on certain real-life situations where this bivariate class has potential applications is also included in Section 4. In Section 5, simulated samples are used to demonstrate how this bivariate class could be used as approximations for bivariate finite-support distributions.
2. Preliminaries
Consider a continuous-time Markov chain (CTMC)
![]() $ \{X(t);\,t\geq 0\} $
with state space
$ \{X(t);\,t\geq 0\} $
with state space
![]() $ \{1,2,\dots,p+1\} $
and generator matrix
$ \{1,2,\dots,p+1\} $
and generator matrix
where
![]() $ \textbf{e} $
denotes a column vector of order p of all ones,
$ \textbf{e} $
denotes a column vector of order p of all ones,
![]() $ \textbf{0} $
denotes a column vector of order p of all zeros, and
$ \textbf{0} $
denotes a column vector of order p of all zeros, and
![]() $ T=[T_{ij}] $
is a
$ T=[T_{ij}] $
is a
![]() $ p\times p $
matrix with
$ p\times p $
matrix with
![]() $ T\textbf{e}\leq \textbf{0}.$
Here, we take
$ T\textbf{e}\leq \textbf{0}.$
Here, we take
![]() $ 1,2,\dots,p $
as transient states and
$ 1,2,\dots,p $
as transient states and
![]() $ p+1 $
as an absorbing state. Now, define
$ p+1 $
as an absorbing state. Now, define
![]() $ \tau =\inf{\{t\geq0;\,X(t)=p+1\} }.$
Let the distribution with which the process starts in one of these states be
$ \tau =\inf{\{t\geq0;\,X(t)=p+1\} }.$
Let the distribution with which the process starts in one of these states be
![]() $ (\pi,\pi_{p+1}) $
. Then the distribution of
$ (\pi,\pi_{p+1}) $
. Then the distribution of
![]() $ \tau $
is called a phase-type distribution with parameters
$ \tau $
is called a phase-type distribution with parameters
![]() $ \pi $
and T, and is denoted by PH
$ \pi $
and T, and is denoted by PH
![]() $(\pi,T)$
. It is known that PH distributions are nondefective and closed under finite mixtures and convolutions [Reference Neuts7], and the PH class is dense in the set of all distributions with support
$(\pi,T)$
. It is known that PH distributions are nondefective and closed under finite mixtures and convolutions [Reference Neuts7], and the PH class is dense in the set of all distributions with support
![]() $ [0, \infty)$
.
$ [0, \infty)$
.
A multidimensional analogue of PH variates was introduced in 1984 [Reference Assaf, Langberg, Savits and Shaked3], and was later modified in [Reference Kulkarni6]. The latter is called the MPH* (multivariate phase*-type) class. For defining a multivariate phase
![]() $ ^{*} $
-type distribution, [Reference Kulkarni6] generalized the above definition of phase-type variates by introducing the concept of rewards. The modified definition is as follows. Consider k exact copies of a CTMC
$ ^{*} $
-type distribution, [Reference Kulkarni6] generalized the above definition of phase-type variates by introducing the concept of rewards. The modified definition is as follows. Consider k exact copies of a CTMC
![]() $ \{X(t);\,t\geq 0\}$
which has all the features as assumed above. For each i,
$ \{X(t);\,t\geq 0\}$
which has all the features as assumed above. For each i,
![]() $1\leq i \leq k $
, let
$1\leq i \leq k $
, let
![]() $ r_{i}(j)$
,
$ r_{i}(j)$
,
![]() $1\leq j\leq p $
, denote the rate at which a reward is obtained when the ith process is in state j. Here, each
$1\leq j\leq p $
, denote the rate at which a reward is obtained when the ith process is in state j. Here, each
![]() $ r_{i}$
,
$ r_{i}$
,
![]() $1\leq i\leq k $
, is a nonnegative p-vector, called the reward vector. Then
$1\leq i\leq k $
, is a nonnegative p-vector, called the reward vector. Then
 \begin{equation*} R=\left(\begin{array}{c}r_{1}\\r_{2}\\\vdots\\r_{k}\end{array}\right) \end{equation*}
\begin{equation*} R=\left(\begin{array}{c}r_{1}\\r_{2}\\\vdots\\r_{k}\end{array}\right) \end{equation*}
is a
![]() $ k\times p$
reward matrix. Now, define
$ k\times p$
reward matrix. Now, define
 \begin{equation} Y_{i}=\int\limits_{0}^{\tau}r_{i}(X(t)) \, {\rm d} t, \qquad 1 \leq i\leq k. \end{equation}
\begin{equation} Y_{i}=\int\limits_{0}^{\tau}r_{i}(X(t)) \, {\rm d} t, \qquad 1 \leq i\leq k. \end{equation}
Then,
![]() $ Y_{i}$
, the total reward accumulated until absorption by the ith process, can be shown to be a PH variate, and the random vector
$ Y_{i}$
, the total reward accumulated until absorption by the ith process, can be shown to be a PH variate, and the random vector
![]() $ (Y_{1},Y_{2},\dots, Y_{k}) $
is said to have a multivariate phase
$ (Y_{1},Y_{2},\dots, Y_{k}) $
is said to have a multivariate phase
![]() $ ^{*} $
-type distribution.
$ ^{*} $
-type distribution.
From the above, it is clear that if
![]() $ r_{i}=\textbf{e}^{\top} $
, where
$ r_{i}=\textbf{e}^{\top} $
, where
![]() $^\top$
stands for transpose, the above definition of
$^\top$
stands for transpose, the above definition of
![]() $ Y_{i} $
coincides with the usual PH variate definition. It was also shown [Reference Kulkarni6] that the MPH* class is closed under finite mixtures, and if MPH
$ Y_{i} $
coincides with the usual PH variate definition. It was also shown [Reference Kulkarni6] that the MPH* class is closed under finite mixtures, and if MPH
![]() $_{n}^{*} $
denotes the set of all n-dimensional distributions in MPH
$_{n}^{*} $
denotes the set of all n-dimensional distributions in MPH
![]() $^{*} $
, then MPH
$^{*} $
, then MPH
![]() $_{n}^{*} $
is dense in the set of all distributions on
$_{n}^{*} $
is dense in the set of all distributions on
![]() $ [0,\infty]^{n}. $
But, many random variables of practical interest have finite support. Hence, a natural question that arises is whether, if we take any finite n-orthotope in
$ [0,\infty]^{n}. $
But, many random variables of practical interest have finite support. Hence, a natural question that arises is whether, if we take any finite n-orthotope in
![]() $[0,\infty]^{n}$
, there exists a class of distributions that is dense and derivable through a construction similar to that adopted in [Reference Kulkarni6]. In the univariate case, one such class was introduced in [Reference Ramaswami and Viswanath8], called finite-support phase-type distributions. Three such classes of distributions were introduced. The first class is defined as follows.
$[0,\infty]^{n}$
, there exists a class of distributions that is dense and derivable through a construction similar to that adopted in [Reference Kulkarni6]. In the univariate case, one such class was introduced in [Reference Ramaswami and Viswanath8], called finite-support phase-type distributions. Three such classes of distributions were introduced. The first class is defined as follows.
Definition 2.1. A random variable X has an FSPH
![]() $_{1}(\pi , T) $
distribution over the interval (a, b),
$_{1}(\pi , T) $
distribution over the interval (a, b),
![]() $ a \lt b $
,
$ a \lt b $
,
![]() $a,b \geq 0 $
, if it has the same distribution as the random variable
$a,b \geq 0 $
, if it has the same distribution as the random variable
![]() $ a + Y \!\mod(b-a) $
, where
$ a + Y \!\mod(b-a) $
, where
![]() $ Y\sim {\rm PH}(\pi, T)$
.
$ Y\sim {\rm PH}(\pi, T)$
.
The set of all FSPH
![]() $_{1} $
distributions over (a, b) is dense in the set of all distributions over (a, b) [Reference Ramaswami and Viswanath8]. In the next section we define and discuss a multidimensional extension of this FSPH class.
$_{1} $
distributions over (a, b) is dense in the set of all distributions over (a, b) [Reference Ramaswami and Viswanath8]. In the next section we define and discuss a multidimensional extension of this FSPH class.
3. The MFSPH class
For defining the multivariate finite-support phase-type distribution, we modify the definition of the FSPH distribution [Reference Ramaswami and Viswanath8] by bringing in the concept of reward vectors.
As in the previous section, consider a CTMC
![]() $ \{X(t);\,t\geq 0\} $
, state space
$ \{X(t);\,t\geq 0\} $
, state space
![]() $ \{1,2,\dots,p+1\} $
, initial distribution
$ \{1,2,\dots,p+1\} $
, initial distribution
![]() $ (\pi,\pi_{p+1}) $
, and generator matrix
$ (\pi,\pi_{p+1}) $
, and generator matrix
where T is an invertible
![]() $ p\times p $
matrix. Define
$ p\times p $
matrix. Define
![]() $ \tau =\inf{\{t\geq0;\,X(t)=p+1\} }$
. Let
$ \tau =\inf{\{t\geq0;\,X(t)=p+1\} }$
. Let
![]() $ r=(r(1),r(2),\dots,r(p)) $
be a nonnegative p-vector. Then, we define a finite-support phase-type distribution with reward vector r as follows.
$ r=(r(1),r(2),\dots,r(p)) $
be a nonnegative p-vector. Then, we define a finite-support phase-type distribution with reward vector r as follows.
Definition 3.1. A random variable Z is said to have an FSPH
![]() $_{1}^{r}(\pi,T)$
distribution (finite-support phase-type distribution of type 1 with parameters
$_{1}^{r}(\pi,T)$
distribution (finite-support phase-type distribution of type 1 with parameters
![]() $ \pi$
, T, and r) over the interval (a, b),
$ \pi$
, T, and r) over the interval (a, b),
![]() $a<b$
, if it has the same distribution as the random variable
$a<b$
, if it has the same distribution as the random variable
![]() $ a + Y \!\mod(b-a)$
, where
$ a + Y \!\mod(b-a)$
, where
![]() $ Y=\int\limits_{0}^{\tau}r(X(t)) \, {\rm d} t$
. The distribution of Y [Reference Kulkarni6] is
$ Y=\int\limits_{0}^{\tau}r(X(t)) \, {\rm d} t$
. The distribution of Y [Reference Kulkarni6] is
where
![]() $ \beta_{+}^{*} $
and
$ \beta_{+}^{*} $
and
![]() $ T_{+}^{*} $
are the matrices obtained from
$ T_{+}^{*} $
are the matrices obtained from
![]() $ \pi $
and T (a method for this is given in Appendix A). Then, we have the following theorem (the proof is similar to the one given in [Reference Ramaswami and Viswanath8]).
$ \pi $
and T (a method for this is given in Appendix A). Then, we have the following theorem (the proof is similar to the one given in [Reference Ramaswami and Viswanath8]).
Theorem 3.1. Let Z be an FSPH
![]() $_{1}^{r}(\pi,T) $
variate over (a, b). Then its probability density function
$_{1}^{r}(\pi,T) $
variate over (a, b). Then its probability density function
![]() $ f({\cdot}) $
and distribution function
$ f({\cdot}) $
and distribution function
![]() $ F({\cdot}) $
are given by
$ F({\cdot}) $
are given by
 \begin{align*} f(z) & = \left\{ \begin{array}{l@{\quad}l} \beta_{+}^{\ast}{\rm e}^{T_{+}^{\ast}(z-a)} (I-{\rm e}^{T_{+}^{\ast}(b-a)})^{-1}({-}T_{+}^{\ast}\textbf{{e}}), &a<z<b , \\[2pt] 0 , & {\rm otherwise} ; \end{array} \right. \\[4pt] F(z) & = \left\{ \begin{array}{l@{\quad}l} 0 , & z\leq a , \\[2pt] \beta_{+}^{\ast}(I-{\rm e}^{T_{+}^{\ast}(z-a)})(I-{\rm e}^{T_{+}^{\ast}(b-a)})^{-1}\textbf{{e}} , & a<z<b , \\[2pt] 1 , & z\geq b. \end{array} \right.\end{align*}
\begin{align*} f(z) & = \left\{ \begin{array}{l@{\quad}l} \beta_{+}^{\ast}{\rm e}^{T_{+}^{\ast}(z-a)} (I-{\rm e}^{T_{+}^{\ast}(b-a)})^{-1}({-}T_{+}^{\ast}\textbf{{e}}), &a<z<b , \\[2pt] 0 , & {\rm otherwise} ; \end{array} \right. \\[4pt] F(z) & = \left\{ \begin{array}{l@{\quad}l} 0 , & z\leq a , \\[2pt] \beta_{+}^{\ast}(I-{\rm e}^{T_{+}^{\ast}(z-a)})(I-{\rm e}^{T_{+}^{\ast}(b-a)})^{-1}\textbf{{e}} , & a<z<b , \\[2pt] 1 , & z\geq b. \end{array} \right.\end{align*}
The density function of Z shows that if we take
![]() $ r=\textbf{e}^\top $
, then FSPH
$ r=\textbf{e}^\top $
, then FSPH
![]() $_{1}^{r}(\pi,T) $
over (a, b) gets reduced to FSPH
$_{1}^{r}(\pi,T) $
over (a, b) gets reduced to FSPH
![]() $_{1}(\pi, T) $
over (a, b). The following corollary is an immediate consequence of the above theorem, obtained by changing the variable in the formula for the density function.
$_{1}(\pi, T) $
over (a, b). The following corollary is an immediate consequence of the above theorem, obtained by changing the variable in the formula for the density function.
Corollary 3.1. A random variable X has an FSPH
![]() $_{1}^{r}(\pi, T) $
distribution over (a, b) if and only if
$_{1}^{r}(\pi, T) $
distribution over (a, b) if and only if
![]() $ \frac{X-a}{b-a} $
has an FSPH
$ \frac{X-a}{b-a} $
has an FSPH
![]() $_{1}^{\frac{r}{b-a}}(\pi, T) $
distribution over (0, 1).
$_{1}^{\frac{r}{b-a}}(\pi, T) $
distribution over (0, 1).
Note that, if
![]() $ r=\textbf{e}^{\top} $
, the random variable X has an FSPH
$ r=\textbf{e}^{\top} $
, the random variable X has an FSPH
![]() $_{1}^{r}(\pi, T) $
distribution over (a, b) if and only if
$_{1}^{r}(\pi, T) $
distribution over (a, b) if and only if
![]() $ \frac{X-a}{b-a} $
has an FSPH
$ \frac{X-a}{b-a} $
has an FSPH
![]() $_{1}^{r}(\pi, (b-a)T) $
distribution over (0, 1).
$_{1}^{r}(\pi, (b-a)T) $
distribution over (0, 1).
Now, to define an MFSPH distribution, we proceed as follows. As assumed at the beginning of this section, consider a CTMC
![]() $ \{X(t);\,t\geq 0\} $
with state space
$ \{X(t);\,t\geq 0\} $
with state space
![]() $ \{1,2,\dots,p+1\} $
, initial distribution
$ \{1,2,\dots,p+1\} $
, initial distribution
![]() $ (\pi,\pi_{p+1}) $
, and generator matrix
$ (\pi,\pi_{p+1}) $
, and generator matrix
where T is an invertible
![]() $ p\times p $
matrix. Define
$ p\times p $
matrix. Define
![]() $ \tau =\inf{\{t\geq0\,:\,X(t)=p+1\} }$
. Let
$ \tau =\inf{\{t\geq0\,:\,X(t)=p+1\} }$
. Let
![]() $ r_{i}=(r_{i}(1),r_{i}(2),\dots,r_{i}(p))$
,
$ r_{i}=(r_{i}(1),r_{i}(2),\dots,r_{i}(p))$
,
![]() $1\leq i\leq k $
, be the nonnegative reward vectors, and
$1\leq i\leq k $
, be the nonnegative reward vectors, and
 \begin{equation*} R=\left(\begin{array}{c} r_{1}\\ r_{2}\\ \vdots\\ r_{k} \end{array}\right) \end{equation*}
\begin{equation*} R=\left(\begin{array}{c} r_{1}\\ r_{2}\\ \vdots\\ r_{k} \end{array}\right) \end{equation*}
the reward matrix of order
![]() $ k \times p $
.
$ k \times p $
.
Definition 3.2. Let
![]() $ Z_{i} =a_{i}+Y_{i} \!\mod(b_{i}-a_{i})$
for some nonnegative real numbers
$ Z_{i} =a_{i}+Y_{i} \!\mod(b_{i}-a_{i})$
for some nonnegative real numbers
![]() $ a_{i},b_{i}$
(
$ a_{i},b_{i}$
(
![]() $a_{i}<b_{i}$
), with
$a_{i}<b_{i}$
), with
![]() $ Y_{i} $
as in (1). Then the random vector
$ Y_{i} $
as in (1). Then the random vector
![]() $ Z=(Z_{1},Z_{2},\dots,Z_{k}) $
is said to follow an MFSPH distribution over
$ Z=(Z_{1},Z_{2},\dots,Z_{k}) $
is said to follow an MFSPH distribution over
![]() $ (a_{1},b_{1})\times(a_{2},b_{2})\times\dots\times(a_{k},b_{k}). $
We denote this as
$ (a_{1},b_{1})\times(a_{2},b_{2})\times\dots\times(a_{k},b_{k}). $
We denote this as
![]() $ {Z\sim {\rm MFSPH}_{1}^{R}(\pi, T)} $
over
$ {Z\sim {\rm MFSPH}_{1}^{R}(\pi, T)} $
over
![]() $(a_{1},b_{1})\times(a_{2},b_{2})\times\dots\times(a_{k},b_{k}). $
$(a_{1},b_{1})\times(a_{2},b_{2})\times\dots\times(a_{k},b_{k}). $
Remark 3.1. Though [Reference Ramaswami and Viswanath8] introduced three classes of FSPH variates, here we consider only the FSPH
![]() $_{1} $
class of variates for the construction of the MFSPH class. So, from here onwards we omit the subscript 1 from the notations for FSPH and MFSPH variates. One can also use the second and third classes of FSPH distributions for defining an MFSPH class. Also, though we generally define the MFSPH class for any finite k-orthotope in
$_{1} $
class of variates for the construction of the MFSPH class. So, from here onwards we omit the subscript 1 from the notations for FSPH and MFSPH variates. One can also use the second and third classes of FSPH distributions for defining an MFSPH class. Also, though we generally define the MFSPH class for any finite k-orthotope in
![]() $[0,\infty)^{k}$
, from here onwards, unless specified, we consider MFSPH distributions with support
$[0,\infty)^{k}$
, from here onwards, unless specified, we consider MFSPH distributions with support
![]() $(0,1)^{k}$
.
$(0,1)^{k}$
.
3.1. Distribution function
Since an MFSPH class is derived from an MPH* class, we can derive the distribution function of an MFSPH variate from that of the corresponding MPH* variate, as shown below.
Theorem 3.2. Let
![]() $ F({\cdot}) $
be the distribution function of an MPH* variate. Then the distribution function of the corresponding MFSPH variate is given by
$ F({\cdot}) $
be the distribution function of an MPH* variate. Then the distribution function of the corresponding MFSPH variate is given by
 \begin{align} \tilde{F}(x) & = \sum\limits_{n_{k}=0}^{\infty}\sum\limits_{n_{k-1}=0}^{\infty}\dots\sum\limits_{n_{1}=0}^{\infty}\bigg[ F(n_{1}+x_{1}, n_{2}+x_{2},\dots, n_{k}+x_{k}) . \nonumber \\
& \quad - \sum\limits_{i=1}^{k}F(n_{1}+x_{1},\dots,n_{i-1}+x_{i-1},n_{i} ,n_{i+1}+x_{i+1},\dots,n_{k}+x_{k}) \notag \\
& \quad +\sum\limits _{i,j=1,i<j}^{k}F(n_{1}+x_{1},\dots , n_{i-1}+x_{i-1},n_{i},n_{i+1}+x_{i+1}, \dots , \notag \\
& \hspace{3cm} n_{j-1} + x_{j-1},n_{j},n_{j+1}+x_{j+1},\dots , n_{k}+x_{k})+\dots \notag \\
& \hspace{6.5cm} +({-}1)^{k}F(n_{1},n_{2},\dots , n_{k})\bigg], \end{align}
\begin{align} \tilde{F}(x) & = \sum\limits_{n_{k}=0}^{\infty}\sum\limits_{n_{k-1}=0}^{\infty}\dots\sum\limits_{n_{1}=0}^{\infty}\bigg[ F(n_{1}+x_{1}, n_{2}+x_{2},\dots, n_{k}+x_{k}) . \nonumber \\
& \quad - \sum\limits_{i=1}^{k}F(n_{1}+x_{1},\dots,n_{i-1}+x_{i-1},n_{i} ,n_{i+1}+x_{i+1},\dots,n_{k}+x_{k}) \notag \\
& \quad +\sum\limits _{i,j=1,i<j}^{k}F(n_{1}+x_{1},\dots , n_{i-1}+x_{i-1},n_{i},n_{i+1}+x_{i+1}, \dots , \notag \\
& \hspace{3cm} n_{j-1} + x_{j-1},n_{j},n_{j+1}+x_{j+1},\dots , n_{k}+x_{k})+\dots \notag \\
& \hspace{6.5cm} +({-}1)^{k}F(n_{1},n_{2},\dots , n_{k})\bigg], \end{align}
where
![]() $ x=(x_{1},x_{2},\dots,x_{k}) $
.
$ x=(x_{1},x_{2},\dots,x_{k}) $
.
Proof. From the definition of an MFSPH distribution, we can see that the MFSPH variate
![]() $X=(X_{1},X_{2},\dots,X_{k}) $
takes values
$X=(X_{1},X_{2},\dots,X_{k}) $
takes values
![]() $(x_{1},x_{2},\dots,x_{k})$
if and only if the corresponding MPH* variate
$(x_{1},x_{2},\dots,x_{k})$
if and only if the corresponding MPH* variate
![]() $ Y =(Y_{1},Y_{2},\dots,Y_{k})$
assumes the values
$ Y =(Y_{1},Y_{2},\dots,Y_{k})$
assumes the values
![]() $(y_{1}+n_{1},y_{2}+n_{2},\dots,y_{k}+n_{k})$
for some vector
$(y_{1}+n_{1},y_{2}+n_{2},\dots,y_{k}+n_{k})$
for some vector
![]() $ (n_{1},n_{2},\dots,n_{k})$
,
$ (n_{1},n_{2},\dots,n_{k})$
,
![]() $n_{1},n_{2},\dots,n_{k}\in \{0,1,2,\dots \} $
. Therefore,
$n_{1},n_{2},\dots,n_{k}\in \{0,1,2,\dots \} $
. Therefore,
 \begin{multline*} \mathbb{P}(X_{1}\leq x_{1},X_{2}\leq x_{2},\dots ,X_{k}\leq x_{k})\\
= \sum\limits_{n_{k}=0}^{\infty}\sum\limits_{n_{k-1}=0}^{\infty}\dots\sum \limits_{n_{1}=0}^{\infty} \mathbb{P}(n_{1}\leq Y_{1}\leq n_{1}+x_{1}, n_{2}\leq Y_{2}\leq n_{2}+x_{2},\dots, n_{k}\leq Y_{k}\leq n_{k}+x_{k}), \end{multline*}
\begin{multline*} \mathbb{P}(X_{1}\leq x_{1},X_{2}\leq x_{2},\dots ,X_{k}\leq x_{k})\\
= \sum\limits_{n_{k}=0}^{\infty}\sum\limits_{n_{k-1}=0}^{\infty}\dots\sum \limits_{n_{1}=0}^{\infty} \mathbb{P}(n_{1}\leq Y_{1}\leq n_{1}+x_{1}, n_{2}\leq Y_{2}\leq n_{2}+x_{2},\dots, n_{k}\leq Y_{k}\leq n_{k}+x_{k}), \end{multline*}
which, on simplification, gives the expression for the distribution function shown in equation (2).□
3.2. Properties
The following are some properties of the MFSPH class of distributions. In many cases these properties directly follow from similar properties of MPH* distributions, and hence we omit the proofs.
-
• Let
 $ X_{1},X_{2},\dots,X_{k} $
be independent random variables in FSPH over (0, 1). Then
$ X_{1},X_{2},\dots,X_{k} $
be independent random variables in FSPH over (0, 1). Then
 $ ( X_{1},X_{2},\dots,X_{k} ) $
is in MFSPH over
$ ( X_{1},X_{2},\dots,X_{k} ) $
is in MFSPH over
 $ (0,1)^{k} $
.
$ (0,1)^{k} $
. -
• Let
 $ ( X_{1},X_{2},\dots,X_{k} ) $
be a random vector following MFSPH over
$ ( X_{1},X_{2},\dots,X_{k} ) $
be a random vector following MFSPH over
 $ (0,1)^{k} $
. Then
$ (0,1)^{k} $
. Then
 $ X_{i}$
,
$ X_{i}$
,
 $1\leq i\leq k $
, follow FSPH distributions over (0, 1).
$1\leq i\leq k $
, follow FSPH distributions over (0, 1). -
• Let
 $ X=( X_{1},X_{2},\dots,X_{k} )$
,
$ X=( X_{1},X_{2},\dots,X_{k} )$
,
 $X_{i} $
independent, be an MFSPH variate over
$X_{i} $
independent, be an MFSPH variate over
 $ (0,1)^{k} $
. Then
$ (0,1)^{k} $
. Then
 $ \sum\limits_{i=1}^{k}X_{i}-\left\lfloor \sum\limits_{i=1}^{k}X_{i}\right\rfloor$
follows an FSPH distribution over (0, 1).
$ \sum\limits_{i=1}^{k}X_{i}-\left\lfloor \sum\limits_{i=1}^{k}X_{i}\right\rfloor$
follows an FSPH distribution over (0, 1). -
• Let
 $ X=( X_{1},X_{2},\dots,X_{k} ) $
be an MFSPH variate over
$ X=( X_{1},X_{2},\dots,X_{k} ) $
be an MFSPH variate over
 $ (0,1)^{k} $
, and let A be an
$ (0,1)^{k} $
, and let A be an
 $ n\times k $
matrix of nonnegative integers. If
$ n\times k $
matrix of nonnegative integers. If
 $Z^{\top}=AX^\top-\lfloor AX^{\top}\rfloor$
, then Z follows an MFSPH distribution over
$Z^{\top}=AX^\top-\lfloor AX^{\top}\rfloor$
, then Z follows an MFSPH distribution over
 $ (0,1)^{k}$
.
$ (0,1)^{k}$
. -
• Let
 $ Y=( Y_{1},Y_{2},\dots,Y_{k} ) $
and
$ Y=( Y_{1},Y_{2},\dots,Y_{k} ) $
and
 $ Z=( Z_{1},Z_{2},\dots,Z_{k} ) $
be independent MFSPH variates over
$ Z=( Z_{1},Z_{2},\dots,Z_{k} ) $
be independent MFSPH variates over
 $ (0,1)^{k} $
and
$ (0,1)^{k} $
and
 $ (0,1)^{m} $
respectively. Then (Y, Z) is an MFSPH variate over
$ (0,1)^{m} $
respectively. Then (Y, Z) is an MFSPH variate over
 $ (0,1)^{k+m} $
.
$ (0,1)^{k+m} $
. -
• The class of MFSPH distributions is closed under finite mixtures.
-
• The class of n-dimensional MFSPH distributions over
 $ (0,1)^{n} $
is dense in the set of all distributions over
$ (0,1)^{n} $
is dense in the set of all distributions over
 $ (0,1)^{n}$
(by using the same argument as in [Reference Assaf, Langberg, Savits and Shaked3]).
$ (0,1)^{n}$
(by using the same argument as in [Reference Assaf, Langberg, Savits and Shaked3]).
4. Estimation of bivariate finite-support phase-type distribution via the EM algorithm
The EM algorithm is a well-known method to compute the maximum likelihood estimates (MLE) of parameters iteratively from observed data. It is applied to problems where the observed data is incomplete or the log-likelihood function of the observed data is too difficult to compute to get the MLE directly from it. It provides a sequence of results from the simple complete data log-likelihood function, thereby avoiding calculations from the complicated incomplete data log-likelihood function. Estimation for PH distributions is of considerable importance when taking into consideration their role in different areas of application. Reference [Reference Asmussen, Nerman and Olsson2] was the first to develop a general approach to maximum likelihood estimation of continuous PH distributions by using the EM algorithm.
The most general form of the MFSPH as formulated in the previous section does not appear to lend itself to a direct application of EM. Although the marginals are phase type and there is indeed characterization of transient distributions of stochastic fluid flows, those are in terms of certain complicated functions of the basic parameters, and that causes severe problems. However, there appear to be certain large subsets of MFSPH for which one can get an explicit form of the likelihood function that lends itself to the application of EM. One such class is the case of unit reward rates and a block upper bidiagonal structure for the subintensity matrix. In this section we develop and illustrate the application of EM for that class in the block
![]() $ 2\times 2 $
case (which is sufficient to make the point that it extends to the general block upper diagonal case). In that case, the bivariate PH variates that are used in the fitted models are the sojourn times in each of the two blocks of states. Indeed, any subclass that lends itself to an explicit form for the joint distribution of the variables and leading to an obvious choice of sufficient statistics can be handled by the methods used here.
$ 2\times 2 $
case (which is sufficient to make the point that it extends to the general block upper diagonal case). In that case, the bivariate PH variates that are used in the fitted models are the sojourn times in each of the two blocks of states. Indeed, any subclass that lends itself to an explicit form for the joint distribution of the variables and leading to an obvious choice of sufficient statistics can be handled by the methods used here.
The special class of bivariate finite-support phase-type (BFSPH) distributions considered in this section can find certain potential applications. For example, in risk theory BFSPH variates can be used to model joint returns of two correlated securities, such as bond index and stock index, over a time period. Similarly, in the insurance field, to model the returns offered by insurance companies from certain policies that are exclusively intended for cover against recurrent diseases such as cancer, these kinds of BFSPH variates can be used. The total return that a patient gets until the time of relapse and the return they get until the time to symptoms can be modelled by these BFSPH variates. Reference [Reference Zelen and Feinleib10] provides a detailed discussion on models related to relapse times of recurrent diseases. For a detailed analysis of the corresponding BPH* distribution, see [Reference Ahlstrom, Olsson and Nerman1].
Let
![]() $ \{ Y(t);\,t\geq0\} $
be a CTMC with state space
$ \{ Y(t);\,t\geq0\} $
be a CTMC with state space
![]() $ E=E_{1}\cup E_{2}\cup\{p+1\}$
, where
$ E=E_{1}\cup E_{2}\cup\{p+1\}$
, where
![]() $ |E_{1}|=p_{1}$
,
$ |E_{1}|=p_{1}$
,
![]() $|E_{2}|=p_{2}$
, and
$|E_{2}|=p_{2}$
, and
![]() $ p=p_{1}+p_{2} $
, and generator matrix
$ p=p_{1}+p_{2} $
, and generator matrix
 \begin{equation*} \left(\begin{array}{c@{\quad}c@{\quad}c} T_{11}&T_{12}&\textbf{0}\\ \textbf{0}&T_{22}& \textbf{t}_{2}\\ \textbf{0}&\textbf{0}&\textbf{0} \end{array}\right)\!, \end{equation*}
\begin{equation*} \left(\begin{array}{c@{\quad}c@{\quad}c} T_{11}&T_{12}&\textbf{0}\\ \textbf{0}&T_{22}& \textbf{t}_{2}\\ \textbf{0}&\textbf{0}&\textbf{0} \end{array}\right)\!, \end{equation*}
with
![]() $ \textbf{t}_{2}=-T_{22}\textbf{e} $
. Assume that
$ \textbf{t}_{2}=-T_{22}\textbf{e} $
. Assume that
![]() $ p+1 $
is an absorbing state and all the other states are transient. Suppose that
$ p+1 $
is an absorbing state and all the other states are transient. Suppose that
![]() $ T_{11} $
and
$ T_{11} $
and
![]() $ T_{22} $
are invertible, and
$ T_{22} $
are invertible, and
![]() $ \textbf{t}_{1}=-T_{11}\textbf{e} $
. Clearly, the Markov chain starts in one of the states in
$ \textbf{t}_{1}=-T_{11}\textbf{e} $
. Clearly, the Markov chain starts in one of the states in
![]() $ E_{1} $
, undergoes transitions among different states in
$ E_{1} $
, undergoes transitions among different states in
![]() $ E_{1} $
, then moves to those in
$ E_{1} $
, then moves to those in
![]() $ E_{2} $
, and is finally absorbed in
$ E_{2} $
, and is finally absorbed in
![]() $ p+1 $
, after spending a random amount of time in
$ p+1 $
, after spending a random amount of time in
![]() $ E_{2} $
. Now, consider the PH variates
$ E_{2} $
. Now, consider the PH variates
![]() $ Y_{1}\sim {\rm PH}_{p_{1}}(\pi_{1},T_{11}) $
and
$ Y_{1}\sim {\rm PH}_{p_{1}}(\pi_{1},T_{11}) $
and
![]() $ Y_{2}\sim {\rm PH}_{p_{2}}(\pi_{2},T_{22}) $
. Reference [Reference Esparza, Nielsen and Bladt5] derives the distribution function of the BPH
$ Y_{2}\sim {\rm PH}_{p_{2}}(\pi_{2},T_{22}) $
. Reference [Reference Esparza, Nielsen and Bladt5] derives the distribution function of the BPH
![]() $^{\ast} $
variate
$^{\ast} $
variate
![]() $ (Y_{1},Y_{2}) $
, which has initial probability vector
$ (Y_{1},Y_{2}) $
, which has initial probability vector
![]() $ \pi=(\pi_{1},\textbf{0}) $
, and reward matrix R and subintensity matrix T given by
$ \pi=(\pi_{1},\textbf{0}) $
, and reward matrix R and subintensity matrix T given by
as
where
![]() $ T_{12} $
satisfies the system
$ T_{12} $
satisfies the system
It is to be noted that the variables of interest here are the sojourn times in the blocks
![]() $ E_{1} $
and
$ E_{1} $
and
![]() $ E_{2} $
. Also, we assert the fact that each marginal is a PH variable. By using Theorem 3.2, we can compute the distribution function of the corresponding BFSPH variate
$ E_{2} $
. Also, we assert the fact that each marginal is a PH variable. By using Theorem 3.2, we can compute the distribution function of the corresponding BFSPH variate
![]() $ (X_{1},X_{2})$
over
$ (X_{1},X_{2})$
over
![]() $ (0,1)^{2} $
, and we get
$ (0,1)^{2} $
, and we get
 \begin{align} \tilde{F}(x_{1},x_{2}) & = \sum\limits_{n_{1}=0}^{\infty}\sum\limits_{n_{2}=0}^{\infty}\Big[\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}(n_{1}+x_{1})})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11} (n_{2}+x_{2})}) \textbf{t}_{2}+\pi_{1}T_{11}^{-1} \notag \\[1pt]
& \quad (I-{\rm e}^{T_{11}n_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11}n_{2}})\textbf{t}_{2}-\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}(n_{1}+x_{1})})T_{12}T_{22}^{-1} \notag \\[1pt]
& \quad (I-{\rm e}^{T_{11}x_{2}})\textbf{t}_{2}-\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}n_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11}(n_{2}+x_{2})})\textbf{t}_{2}\Big] \notag \\[1pt]
& = \pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}})^{-1}(I-{\rm e}^{T_{11}x_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{22}})^{-1}(I-{\rm e}^{T_{11}x_{2}})\textbf{t}_{2}. \end{align}
\begin{align} \tilde{F}(x_{1},x_{2}) & = \sum\limits_{n_{1}=0}^{\infty}\sum\limits_{n_{2}=0}^{\infty}\Big[\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}(n_{1}+x_{1})})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11} (n_{2}+x_{2})}) \textbf{t}_{2}+\pi_{1}T_{11}^{-1} \notag \\[1pt]
& \quad (I-{\rm e}^{T_{11}n_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11}n_{2}})\textbf{t}_{2}-\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}(n_{1}+x_{1})})T_{12}T_{22}^{-1} \notag \\[1pt]
& \quad (I-{\rm e}^{T_{11}x_{2}})\textbf{t}_{2}-\pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}n_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{11}(n_{2}+x_{2})})\textbf{t}_{2}\Big] \notag \\[1pt]
& = \pi_{1}T_{11}^{-1}(I-{\rm e}^{T_{11}})^{-1}(I-{\rm e}^{T_{11}x_{1}})T_{12}T_{22}^{-1}(I-{\rm e}^{T_{22}})^{-1}(I-{\rm e}^{T_{11}x_{2}})\textbf{t}_{2}. \end{align}
In the following section we discuss how the EM procedure can be used for the estimation of the parameters of the BFSPH variate
![]() $ (X_{1},X_{2}). $
$ (X_{1},X_{2}). $
4.1. An EM algorithm
Assume that a random sample
![]() $ (x_{11},x_{21}),(x_{12},x_{22}),\dots,(x_{1n},x_{2n}) $
on
$ (x_{11},x_{21}),(x_{12},x_{22}),\dots,(x_{1n},x_{2n}) $
on
![]() $ (X_{1},X_{2}) $
is given. Clearly,
$ (X_{1},X_{2}) $
is given. Clearly,
![]() $ (X_{1},X_{2})=(Y_{1},Y_{2})-(\lfloor Y_{1}\rfloor,\lfloor Y_{2}\rfloor) $
, where
$ (X_{1},X_{2})=(Y_{1},Y_{2})-(\lfloor Y_{1}\rfloor,\lfloor Y_{2}\rfloor) $
, where
![]() $ (Y_{1},Y_{2}) $
is a BPH* variate of order
$ (Y_{1},Y_{2}) $
is a BPH* variate of order
![]() $ p=p_{1}+p_{2} $
with distribution function (3). Our objective here is to estimate the parameters of the BFSPH distribution by estimating them for the corresponding BPH
$ p=p_{1}+p_{2} $
with distribution function (3). Our objective here is to estimate the parameters of the BFSPH distribution by estimating them for the corresponding BPH
![]() $^{*} $
distribution. Here, we are applying the EM algorithm by suitably modifying the procedure applied for the BPH* case in [Reference Esparza, Nielsen and Bladt5]. We start by recalling the EM algorithm for a BPH* distribution.
$^{*} $
distribution. Here, we are applying the EM algorithm by suitably modifying the procedure applied for the BPH* case in [Reference Esparza, Nielsen and Bladt5]. We start by recalling the EM algorithm for a BPH* distribution.
4.1.1. Maximum likelihood estimates for BPH
 ${}^{\ast}$
sample
${}^{\ast}$
sample
Let
![]() $ (y^{(1)}_{i},y_{i}^{(2)})$
,
$ (y^{(1)}_{i},y_{i}^{(2)})$
,
![]() $1\leq i\leq m $
, be a random sample from the BPH* distribution described above. For each observation included in this sample there will be a trajectory of the underlying CTMC; suppose that we can observe this trajectory. These trajectories will represent the complete sample. In this scenario, one can write the joint likelihood of the complete sample, say
$1\leq i\leq m $
, be a random sample from the BPH* distribution described above. For each observation included in this sample there will be a trajectory of the underlying CTMC; suppose that we can observe this trajectory. These trajectories will represent the complete sample. In this scenario, one can write the joint likelihood of the complete sample, say
![]() $ (x_{(1)},x_{(2)}) $
, as [Reference Esparza, Nielsen and Bladt5]
$ (x_{(1)},x_{(2)}) $
, as [Reference Esparza, Nielsen and Bladt5]
 \begin{eqnarray*} L_{f}(\theta ;\ x_{(1)},x_{(2)})\ &=&\ \prod\limits_{i=1}^{p_{1}}\pi_{i}^{B_{i}} \prod\limits_{i=1}^{p_{1}}\prod\limits_{j=1,j\neq i}^{p_{1}}t_{ij}^{N_{ij}}{\rm e}^{t_{ij}Z_{i}}\prod\limits_{i=1}^{p_{1}} \prod\limits_{j=p_{1}+1}^{p}t_{ij}^{N_{ij}}\\ &&\prod\limits_{i=p_{1}+1}^{p} \prod\limits_{j=p_{1}+1,j\neq i}^{p}t_{ij}^{N_{ij}}{\rm e}^{-t_{ij}Z_{i}}\prod\limits_{i=p_{1}+1}^{p}t_{i}^{N_{i}}{\rm e}^{-t_{i}Z_{i}} , \end{eqnarray*}
\begin{eqnarray*} L_{f}(\theta ;\ x_{(1)},x_{(2)})\ &=&\ \prod\limits_{i=1}^{p_{1}}\pi_{i}^{B_{i}} \prod\limits_{i=1}^{p_{1}}\prod\limits_{j=1,j\neq i}^{p_{1}}t_{ij}^{N_{ij}}{\rm e}^{t_{ij}Z_{i}}\prod\limits_{i=1}^{p_{1}} \prod\limits_{j=p_{1}+1}^{p}t_{ij}^{N_{ij}}\\ &&\prod\limits_{i=p_{1}+1}^{p} \prod\limits_{j=p_{1}+1,j\neq i}^{p}t_{ij}^{N_{ij}}{\rm e}^{-t_{ij}Z_{i}}\prod\limits_{i=p_{1}+1}^{p}t_{i}^{N_{i}}{\rm e}^{-t_{i}Z_{i}} , \end{eqnarray*}
where
![]() $ B_{i} $
is the number of processes starting in state i,
$ B_{i} $
is the number of processes starting in state i,
![]() $ N_{i} $
is the number of processes exiting from state i to the absorbing state,
$ N_{i} $
is the number of processes exiting from state i to the absorbing state,
![]() $ Z_{i} $
is the total time spent in state i, and
$ Z_{i} $
is the total time spent in state i, and
![]() $ N_{ij} $
is the number of jumps from state i to state j among all processes. These statistics jointly form a set of sufficient statistics for the parameters
$ N_{ij} $
is the number of jumps from state i to state j among all processes. These statistics jointly form a set of sufficient statistics for the parameters
![]() $ \pi $
and T. The routine maximization of the above likelihood function would yield the maximum likelihood estimates of the parameters as
$ \pi $
and T. The routine maximization of the above likelihood function would yield the maximum likelihood estimates of the parameters as
 \begin{equation} \hat{\pi_{i}}=\dfrac{B_{i}}{m}, \qquad \hat{T}_{ij}=\dfrac{N_{ij}}{Z_{i}}, \qquad \hat{t}_{i}=\dfrac{N_{i}}{Z_{i}}, \qquad \hat{T}_{ii}=-\left( \hat{t_{i}}+\sum\limits_{j=1,j\neq i}^{p}\hat{T_{ij}}\right)\!. \end{equation}
\begin{equation} \hat{\pi_{i}}=\dfrac{B_{i}}{m}, \qquad \hat{T}_{ij}=\dfrac{N_{ij}}{Z_{i}}, \qquad \hat{t}_{i}=\dfrac{N_{i}}{Z_{i}}, \qquad \hat{T}_{ii}=-\left( \hat{t_{i}}+\sum\limits_{j=1,j\neq i}^{p}\hat{T_{ij}}\right)\!. \end{equation}
But in practical cases we will not have the complete sample from the BPH* distribution. Instead, the available sample observations only give us the total sojourn times of the processes in concerned blocks (for example, in
![]() $(y^{(1)}_{k},y_{k}^{(2)})$
,
$(y^{(1)}_{k},y_{k}^{(2)})$
,
![]() $y^{(1)}_{k} $
represents the total sojourn time in
$y^{(1)}_{k} $
represents the total sojourn time in
![]() $ E_{1} $
of the kth replica of the process until it enters states in
$ E_{1} $
of the kth replica of the process until it enters states in
![]() $ E_{2} $
, and
$ E_{2} $
, and
![]() $ y_{k}^{(2)} $
denotes the sojourn time of this process in
$ y_{k}^{(2)} $
denotes the sojourn time of this process in
![]() $ E_{2} $
until it gets absorbed in
$ E_{2} $
until it gets absorbed in
![]() $ p+1 $
). In this case, we consider the set of sufficient statistics as missing and estimate them, based on whatever is observed, using the estimation part of the EM procedure.
$ p+1 $
). In this case, we consider the set of sufficient statistics as missing and estimate them, based on whatever is observed, using the estimation part of the EM procedure.
To execute the EM algorithm we start with a trial set of parameters, which are used to obtain the estimates of the missing set of sufficient statistics given by (14)–(17) in Appendix B (for details on the computation of these estimates, see [Reference Esparza, Nielsen and Bladt5]). This is the E step in the EM procedure. Then, these estimates are used with (6) to obtain a new set of parameter estimates, which is the maximization step. This process is then repeated with the new parameter estimates until we get limiting values for them (for a discussion on the convergence of this procedure, see [Reference Asmussen, Nerman and Olsson2]).
4.2. Estimation of sufficient statistics for BFSPH
Corresponding to a single sample
![]() $ x=(x_{1},x_{2}) $
on a BFSPH
$ x=(x_{1},x_{2}) $
on a BFSPH
![]() $_{1}^{R}(\pi,T)$
variate, which is defined over
$_{1}^{R}(\pi,T)$
variate, which is defined over
![]() $ (0,1)\times (0,1)$
and has distribution function (5), the observation
$ (0,1)\times (0,1)$
and has distribution function (5), the observation
![]() $ y=x+n$
, for some
$ y=x+n$
, for some
![]() $ n=(n_{1},n_{2})$
,
$ n=(n_{1},n_{2})$
,
![]() $n_{1},n_{2}\in \{0,1,2,3,\dots\}$
and
$n_{1},n_{2}\in \{0,1,2,3,\dots\}$
and
![]() $ y=(y_{1},y_{2}) $
, is a sample on a BPH
$ y=(y_{1},y_{2}) $
, is a sample on a BPH
![]() $^{*}(\pi, T) $
variate with the distribution function (3). Hence, to estimate the parameters of a BFSPH distribution we can use the EM algorithm for the BPH* distribution by treating n as a missing value and evaluating all the other required conditional expectations, given x via the conditional expectations, given both x and y.
$^{*}(\pi, T) $
variate with the distribution function (3). Hence, to estimate the parameters of a BFSPH distribution we can use the EM algorithm for the BPH* distribution by treating n as a missing value and evaluating all the other required conditional expectations, given x via the conditional expectations, given both x and y.
To calculate the estimated values of the sufficient statistics, first of all define
 \begin{equation*} M(z,\textbf{e}_{i},\textbf{e}_{j},T)=\int\limits_{0}^{z} {\rm e}^{Tu}\textbf{e}_{i}\textbf{e}_{j}^{\top}{\rm e}^{T(z-u)} \, {\rm d} u , \end{equation*}
\begin{equation*} M(z,\textbf{e}_{i},\textbf{e}_{j},T)=\int\limits_{0}^{z} {\rm e}^{Tu}\textbf{e}_{i}\textbf{e}_{j}^{\top}{\rm e}^{T(z-u)} \, {\rm d} u , \end{equation*}
where z is an observation either from PH
![]() $^{\textbf{e}}(\pi_{1},T_{11}) $
or from PH
$^{\textbf{e}}(\pi_{1},T_{11}) $
or from PH
![]() $^{\textbf{e}}(\pi_{2},T_{22})$
, and
$^{\textbf{e}}(\pi_{2},T_{22})$
, and
![]() $\textbf{e}_{i}$
is a column vector of appropriate dimension having 1 as the only nonzero element, which occurs at the ith position. Then, to evaluate
$\textbf{e}_{i}$
is a column vector of appropriate dimension having 1 as the only nonzero element, which occurs at the ith position. Then, to evaluate
![]() $ M(z,\textbf{e}_{i},\textbf{e}_{j},T) $
we use the following theorem, which results from the formula for computing integrals involving matrix exponentials [Reference Van Loan9]. We omit the proof since it follows easily from this formula by making some simple modifications.
$ M(z,\textbf{e}_{i},\textbf{e}_{j},T) $
we use the following theorem, which results from the formula for computing integrals involving matrix exponentials [Reference Van Loan9]. We omit the proof since it follows easily from this formula by making some simple modifications.
Theorem 4.1. Let
 \begin{equation*} \Upsilon_{i}=[\mathbf{0} \; \mathbf{0}\;\cdots\;\mathbf{0}\; I\; \mathbf{0}\;\cdots\;\mathbf{0}\;] , \qquad C=\left(\begin{array}{c@{\quad}c} T& e_{i}e_{j}^{\top}\\[7pt] \mathbf{0} & T\end{array}\right)\!,\end{equation*}
\begin{equation*} \Upsilon_{i}=[\mathbf{0} \; \mathbf{0}\;\cdots\;\mathbf{0}\; I\; \mathbf{0}\;\cdots\;\mathbf{0}\;] , \qquad C=\left(\begin{array}{c@{\quad}c} T& e_{i}e_{j}^{\top}\\[7pt] \mathbf{0} & T\end{array}\right)\!,\end{equation*}
where I, the identity matrix of order p, appears as the ith block in
![]() $\Upsilon_{i} $
, and
$\Upsilon_{i} $
, and
![]() $ \textbf{{0}} $
is the zero matrix of order p. Then
$ \textbf{{0}} $
is the zero matrix of order p. Then
The following theorem provides estimates of the sufficient statistics for the parameters of the BFSPH variate when we are observing only the fractional vector of the BPH* random variable.
Theorem 4.2. Assume that we have a sample fractional part vector
![]() $ x=(x_{1},x_{2}) $
, with distribution function (5), of a BPH* variate
$ x=(x_{1},x_{2}) $
, with distribution function (5), of a BPH* variate
![]() $ (Y_{1},Y_{2})$
. Define
$ (Y_{1},Y_{2})$
. Define
 \begin{align*} a(x) & = {\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , \\ b(x) & = \pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1} , \\ c(x) & = \dfrac{1}{\pi_{1}a(x)}.\end{align*}
\begin{align*} a(x) & = {\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , \\ b(x) & = \pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1} , \\ c(x) & = \dfrac{1}{\pi_{1}a(x)}.\end{align*}
Let
![]() $M^{*}(x,\textbf{{e}}_{i},\textbf{{e}}_{j},T)=\sum\limits_{n=0}^{\infty}M(x+n,\textbf{{e}}_{i},\textbf{{e}}_{j},T)$
and
$M^{*}(x,\textbf{{e}}_{i},\textbf{{e}}_{j},T)=\sum\limits_{n=0}^{\infty}M(x+n,\textbf{{e}}_{i},\textbf{{e}}_{j},T)$
and
![]() $ i^{*}=i-p_{1}$
. Then the conditional expectations, given x, of the sufficient statistics for the parameters are given by
$ i^{*}=i-p_{1}$
. Then the conditional expectations, given x, of the sufficient statistics for the parameters are given by
 \begin{equation}\hat{Z_{i}} = \left\{ \begin{array}{l@{\quad}l} c(x)\pi_{1}M^{*}(x_{1},\textbf{{e}}_{i},\textbf{{e}}_{i},T_{11})T_{12} {\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}T_{2} , & \quad 1\leq i\leq p_{1}\kern-1pt ; \\[3pt] c(x)\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}M^{*}(x_{2},\textbf{{e}}_{i},\textbf{{e}}_{i},T_{22})\textbf{{t}}_{2} , & \quad p_{1}+1\leq i\leq p ; \end{array}\right.\qquad\qquad\end{equation}
\begin{equation}\hat{Z_{i}} = \left\{ \begin{array}{l@{\quad}l} c(x)\pi_{1}M^{*}(x_{1},\textbf{{e}}_{i},\textbf{{e}}_{i},T_{11})T_{12} {\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}T_{2} , & \quad 1\leq i\leq p_{1}\kern-1pt ; \\[3pt] c(x)\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}M^{*}(x_{2},\textbf{{e}}_{i},\textbf{{e}}_{i},T_{22})\textbf{{t}}_{2} , & \quad p_{1}+1\leq i\leq p ; \end{array}\right.\qquad\qquad\end{equation}
 \begin{equation} \hat{N}_{ij} = \left\{ \begin{array}{l@{\quad\ \ }l} (T_{11})_{ij}c(x)\pi_{1}M^{*}(x_{1},\textbf{{e}}_{i},\textbf{{e}}_{j},T_{11}) T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , &\! 1\leq i , j \leq p_{1}\kern-1pt ; \\[3pt] (T_{12})_{ij^{*}}c(x)\pi_{1}{\rm e}^{T_{11}x_{1}} (I-{\rm e}^{T_{11}})^{-1} \textbf{{e}}_{i}\textbf{{e}}_{j}^{\top}{\rm e}^{T_{22}x_{2}} (I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , &\! 1\leq i\leq p_{1}\kern-1pt , \\[3pt] &\! p_{1}+1\leq j\leq p; \\[3pt] (T_{22})_{i^{*}j^{*}}c(x)\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12} M^{*}(x_{2},\textbf{{e}}_{i^{*}},\textbf{{e}}_{j^{*}},T_{22})\textbf{{t}}_{2} , &\! p_{1}+1\leq i , j \leq p . \end{array} \right. \end{equation}
\begin{equation} \hat{N}_{ij} = \left\{ \begin{array}{l@{\quad\ \ }l} (T_{11})_{ij}c(x)\pi_{1}M^{*}(x_{1},\textbf{{e}}_{i},\textbf{{e}}_{j},T_{11}) T_{12}{\rm e}^{T_{22}x_{2}}(I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , &\! 1\leq i , j \leq p_{1}\kern-1pt ; \\[3pt] (T_{12})_{ij^{*}}c(x)\pi_{1}{\rm e}^{T_{11}x_{1}} (I-{\rm e}^{T_{11}})^{-1} \textbf{{e}}_{i}\textbf{{e}}_{j}^{\top}{\rm e}^{T_{22}x_{2}} (I-{\rm e}^{T_{22}})^{-1}\textbf{{t}}_{2} , &\! 1\leq i\leq p_{1}\kern-1pt , \\[3pt] &\! p_{1}+1\leq j\leq p; \\[3pt] (T_{22})_{i^{*}j^{*}}c(x)\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12} M^{*}(x_{2},\textbf{{e}}_{i^{*}},\textbf{{e}}_{j^{*}},T_{22})\textbf{{t}}_{2} , &\! p_{1}+1\leq i , j \leq p . \end{array} \right. \end{equation}
Proof. From [Reference Esparza, Nielsen and Bladt5] we can see that
![]() $ Y_{1}\sim {\rm PH}(\pi_{1},T_{11}) $
and
$ Y_{1}\sim {\rm PH}(\pi_{1},T_{11}) $
and
![]() $ Y_{2}\sim {\rm PH}(\pi_{2},T_{22})$
. Now, consider the sufficient statistic
$ Y_{2}\sim {\rm PH}(\pi_{2},T_{22})$
. Now, consider the sufficient statistic
![]() $ B_{i} $
, the number of processes starting in state i for
$ B_{i} $
, the number of processes starting in state i for
![]() $ i=1,2,\dots,p_{1} $
. It can be viewed as a random variable that takes the value 1 if the underlying Markov process starts in state i and 0 otherwise. Hence,
$ i=1,2,\dots,p_{1} $
. It can be viewed as a random variable that takes the value 1 if the underlying Markov process starts in state i and 0 otherwise. Hence,
 \begin{align*}\hat{ B}_{i} & = \mathbb{E}[B_{i} \mid X_{1}=x_{1},X_{2}=x_{2}] \\ & = \mathbb{P}[X(0)=i\mid X_{1}=x_{1},X_{2}=x_{2}] \\ & = \dfrac{\sum\limits_{n_{1}=0}^{\infty}\sum\limits_{n_{2}=0}^{\infty}\mathbb{P}\big[X(0)=i, Y_{1}=n_{1}+x_{1},Y_{2}=n_{2}+x_{2}\big]}{\mathbb{P}\big[x_{1}<X_{1}\leq x_{1}+{\rm d} x_{1},x_{2}<X_{2}\leq x_{2}+ {\rm d} x_{2}\big]} \end{align*}
\begin{align*}\hat{ B}_{i} & = \mathbb{E}[B_{i} \mid X_{1}=x_{1},X_{2}=x_{2}] \\ & = \mathbb{P}[X(0)=i\mid X_{1}=x_{1},X_{2}=x_{2}] \\ & = \dfrac{\sum\limits_{n_{1}=0}^{\infty}\sum\limits_{n_{2}=0}^{\infty}\mathbb{P}\big[X(0)=i, Y_{1}=n_{1}+x_{1},Y_{2}=n_{2}+x_{2}\big]}{\mathbb{P}\big[x_{1}<X_{1}\leq x_{1}+{\rm d} x_{1},x_{2}<X_{2}\leq x_{2}+ {\rm d} x_{2}\big]} \end{align*}
as
![]() $ {\rm d} x_{1}\rightarrow 0 $
and
$ {\rm d} x_{1}\rightarrow 0 $
and
![]() $ {\rm d} x_{2}\rightarrow 0$
, which on simplification gives (7). The other estimates are obtained in a similar manner.
$ {\rm d} x_{2}\rightarrow 0$
, which on simplification gives (7). The other estimates are obtained in a similar manner.
Remark 4.1. We can use the above theorem for finding estimates of the sufficient statistics even for cases with nonunit reward rates. For example, consider a BPH* variate with a more general reward matrix
where
![]() $ R_{1}$
and
$ R_{1}$
and
![]() $ R_{2}$
are nonunit (
$ R_{2}$
are nonunit (
![]() $\neq \textbf{e} $
) reward vectors of order
$\neq \textbf{e} $
) reward vectors of order
![]() $ p_{1} $
and
$ p_{1} $
and
![]() $ p_{2} $
respectively. The distribution function in this case is
$ p_{2} $
respectively. The distribution function in this case is
Here,
![]() $\tilde{T}_{11} = \Delta(R_{1})^{-1}T_{11}$
,
$\tilde{T}_{11} = \Delta(R_{1})^{-1}T_{11}$
,
![]() $\tilde{T}_{12} = \Delta(R_{1})^{-1}T_{12}$
,
$\tilde{T}_{12} = \Delta(R_{1})^{-1}T_{12}$
,
![]() $\tilde{T}_{22} = \Delta(R_{2})^{-1}T_{22}$
, and
$\tilde{T}_{22} = \Delta(R_{2})^{-1}T_{22}$
, and
![]() $\tilde{\textbf{t}}_{2} = \Delta(R_{2})^{-1}\textbf{t}_{2}$
, where
$\tilde{\textbf{t}}_{2} = \Delta(R_{2})^{-1}\textbf{t}_{2}$
, where
![]() $\Delta(R_{i})$
,
$\Delta(R_{i})$
,
![]() $i=1, 2$
, denote the diagonal matrix having elements of
$i=1, 2$
, denote the diagonal matrix having elements of
![]() $ R_{i}$
as its entries, and
$ R_{i}$
as its entries, and
![]() $ \tilde{T}_{12} $
is the solution of the system
$ \tilde{T}_{12} $
is the solution of the system
It is to be noted that the distribution functions given in (3) and (11) have similar expressions. So, the whole theory developed for the estimation of parameters of BFSPH variates discussed above in the unit reward rate case can be easily extended to cover BFSPH variates in the nonunit reward rate case considered here.
Remark 4.2. Another way of obtaining the above estimates for the sufficient statistics for BFSPH, if the estimates of the sufficient statistics for the parameters of the corresponding BPH* variate are available, is given in Appendix B.
For the computation of
![]() $ M^{*}(x,\textbf{e}_{i},\textbf{e}_{j},T) $
appearing in Theorem 4.2, we use the following theorem.
$ M^{*}(x,\textbf{e}_{i},\textbf{e}_{j},T) $
appearing in Theorem 4.2, we use the following theorem.
Theorem 4.3. The matrix
![]() $ M^{*}(x,\textbf{{e}}_{i},\textbf{{e}}_{j},T) $
is given by
$ M^{*}(x,\textbf{{e}}_{i},\textbf{{e}}_{j},T) $
is given by
Proof. Using the definition of
![]() $M(x,\textbf{e}_{i},\textbf{e}_{j},T)$
, we have
$M(x,\textbf{e}_{i},\textbf{e}_{j},T)$
, we have
In particular, when
![]() $ y=n $
, a positive integer,
$ y=n $
, a positive integer,
Summing (12) over n yields the stated result.
Once the estimates of the sufficient statistics are obtained, the maximum likelihood estimates of
![]() $ \pi $
and T based on a sample of m observations are computed by
$ \pi $
and T based on a sample of m observations are computed by
 \begin{equation}{}\hat{\pi_{i}}=\dfrac{\sum\limits_{k}B^{[k]}_{i}}{m}, \quad \hat{T}_{ij}=\dfrac{\sum\limits_{k}N_{ij}^{[k]}}{\sum\limits_{k}Z_{i}^{[k]}}, \quad \hat{\textbf{t}}_{i}=\dfrac{\sum\limits_{k}N^{[k]}_{i}}{\sum\limits_{k}Z^{[k]}_{i}}, \quad \hat{T}_{ii}=-\left( \hat{\textbf{t}_{i}}+\sum\limits_{j=1,j\neq i}^{p}\hat{T_{ij}}\right)\!, \end{equation}
\begin{equation}{}\hat{\pi_{i}}=\dfrac{\sum\limits_{k}B^{[k]}_{i}}{m}, \quad \hat{T}_{ij}=\dfrac{\sum\limits_{k}N_{ij}^{[k]}}{\sum\limits_{k}Z_{i}^{[k]}}, \quad \hat{\textbf{t}}_{i}=\dfrac{\sum\limits_{k}N^{[k]}_{i}}{\sum\limits_{k}Z^{[k]}_{i}}, \quad \hat{T}_{ii}=-\left( \hat{\textbf{t}_{i}}+\sum\limits_{j=1,j\neq i}^{p}\hat{T_{ij}}\right)\!, \end{equation}
where
![]() $B_{i}^{[k]}$
,
$B_{i}^{[k]}$
,
![]() $N_{i}^{[k]}$
,
$N_{i}^{[k]}$
,
![]() $N_{ij}^{[k]}$
, and
$N_{ij}^{[k]}$
, and
![]() $Z_{i}^{[k]}$
are the statistics, analogous to
$Z_{i}^{[k]}$
are the statistics, analogous to
![]() $B_{i}$
,
$B_{i}$
,
![]() $N_{i}$
,
$N_{i}$
,
![]() $N_{ij}$
, and
$N_{ij}$
, and
![]() $Z_{i}$
defined above, related to the kth process.
$Z_{i}$
defined above, related to the kth process.
Thus, the EM procedure adopted here can be summarised as follows. First, start with some crude estimates of the parameters
![]() $ \pi $
and T, and use those values to get the estimates of the sufficient statistics
$ \pi $
and T, and use those values to get the estimates of the sufficient statistics
![]() $ B_{i}$
,
$ B_{i}$
,
![]() $N_{i}$
,
$N_{i}$
,
![]() $N_{ij}$
, and
$N_{ij}$
, and
![]() $ Z_{i} $
by applying (7)–(10). These estimates of sufficient statistics and (13) are then used to get the updated values of
$ Z_{i} $
by applying (7)–(10). These estimates of sufficient statistics and (13) are then used to get the updated values of
![]() $ \pi $
and T. This process is repeated until we get reasonably good approximations for the estimates of the parameters
$ \pi $
and T. This process is repeated until we get reasonably good approximations for the estimates of the parameters
![]() $ \pi $
and T.
$ \pi $
and T.
5. Numerical results
To illustrate the performance of the estimation algorithm that has been developed for BFSPH variates in Section 4, we present some numerical examples here. In these examples we demonstrate how the fitted distributions give reasonably good approximations for the population from which the samples are taken. In all these examples we generate data from some bivariate probability distributions with finite support and fit them with suitable functions of bivariate finite-support phase-type variates by using the EM algorithm. In all these cases, one component is taken as some random variate X with support [0, 1], and the other is defined using a regression equation
![]() $Y=aX+b+\varepsilon$
, where
$Y=aX+b+\varepsilon$
, where
![]() $ \varepsilon $
is a stochastic error term following a continuous distribution.
$ \varepsilon $
is a stochastic error term following a continuous distribution.
Example 5.1. As a first illustration, we take the first component X of the bivariate sample as a gamma variate. We generate 10 000 observations from the gamma G(2, 2) distribution. The graph of the density of G(2, 2) gives the impression that, even though the gamma variate is a nonnegative random variable defined on the whole positive real line, it can be approximated reasonably well by a distribution having finite support [0, 20]. In order to normalize the observations to the range [0, 1], we divide each of them by 20. Then we generate another 10 000 observations from the exp(1.5) distribution and divide each observation by 15. The second component Y is taken as
![]() $ Y=0.5X+\varepsilon$
,
$ Y=0.5X+\varepsilon$
,
![]() $\varepsilon \sim \dfrac{1}{15} {\rm exp}(1.5)$
. A three-dimensional histogram is generated for the bivariate random vector (X, Y), and the histogram gives us the impression that it can be approximated reasonably well by a distribution having support
$\varepsilon \sim \dfrac{1}{15} {\rm exp}(1.5)$
. A three-dimensional histogram is generated for the bivariate random vector (X, Y), and the histogram gives us the impression that it can be approximated reasonably well by a distribution having support
![]() $ [0, 1]^{2}$
. The data is fitted with a BFSPH distribution of order 6 (see Figure 1). The mean, variances, and correlation coefficients of the simulated data and their estimated values are shown in table 1.
$ [0, 1]^{2}$
. The data is fitted with a BFSPH distribution of order 6 (see Figure 1). The mean, variances, and correlation coefficients of the simulated data and their estimated values are shown in table 1.
Table 1: Comparison of observed and estimated values of some moments of the BFSPH distribution with
![]() $X\sim {\rm normalized}\ G(2,2)$
variate over [0, 1], and
$X\sim {\rm normalized}\ G(2,2)$
variate over [0, 1], and
![]() $Y=0.5X+ \varepsilon$
,
$Y=0.5X+ \varepsilon$
,
![]() $\varepsilon \sim \frac{1}{15}{\rm exp}(1.5)$
.
$\varepsilon \sim \frac{1}{15}{\rm exp}(1.5)$
.


Figure 1:
Bivariate finite support vector (X, Y), X a normalized G(2, 2) variate over [0, 1],
![]() $ Y=0.5X+\varepsilon$
,
$ Y=0.5X+\varepsilon$
,
![]() $\varepsilon \sim \dfrac{1}{15}{\rm exp}(1.5)$
, fitted with a BFSPH distribution of order 6.
$\varepsilon \sim \dfrac{1}{15}{\rm exp}(1.5)$
, fitted with a BFSPH distribution of order 6.
Example 5.2. As another example, 10 000 observations are generated from a beta
![]() $ B(0.5,5) $
distribution, which is assumed as the distribution of X. We take
$ B(0.5,5) $
distribution, which is assumed as the distribution of X. We take
![]() $ Y=0.3X+\varepsilon $
, where
$ Y=0.3X+\varepsilon $
, where
![]() $ \varepsilon$
is Erlang of order 2 with scale parameter 1.5. The graph of the density of
$ \varepsilon$
is Erlang of order 2 with scale parameter 1.5. The graph of the density of
![]() $ {\rm Erlang}(2,1.5) $
shows that it can be approximated reasonably well by a distribution having finite support [0, 25]. In order to normalize the observations to the range [0, 1], we divide each of them by 25. A three-dimensional histogram is plotted for the bivariate random vector (X, Y), and the data fitted with a BFSPH variate of order 4. A three-dimensional histogram constructed from the bivariate data and the fitted density is shown in Figure 2. Table 2 shows a comparison of the observed and estimated values of some moments.
$ {\rm Erlang}(2,1.5) $
shows that it can be approximated reasonably well by a distribution having finite support [0, 25]. In order to normalize the observations to the range [0, 1], we divide each of them by 25. A three-dimensional histogram is plotted for the bivariate random vector (X, Y), and the data fitted with a BFSPH variate of order 4. A three-dimensional histogram constructed from the bivariate data and the fitted density is shown in Figure 2. Table 2 shows a comparison of the observed and estimated values of some moments.
Example 5.3. Here, X is taken as a lognormal variate and Y is defined using the regression equation
![]() $Y=5X+1+\varepsilon $
, where
$Y=5X+1+\varepsilon $
, where
![]() $ \varepsilon $
is uniform over
$ \varepsilon $
is uniform over
![]() $ ({-}1,1) $
. In this case we need a BFSPH distribution of order at least 6 to get a good fit for the data. To construct the three-dimensional histogram we generate 10 000 observations from a lognormal distribution with
$ ({-}1,1) $
. In this case we need a BFSPH distribution of order at least 6 to get a good fit for the data. To construct the three-dimensional histogram we generate 10 000 observations from a lognormal distribution with
![]() $ \mu=0.1 $
and
$ \mu=0.1 $
and
![]() $ \sigma=0.35 $
, and divide each term by 4.5. By doing so we get a lognormal distribution which is approximated by a distribution with support on a finite interval (normalized to [0, 1]). The three-dimensional histogram constructed in this way and the fitted joint probability density function (using a BFSPH distribution of order 7) are shown in Figure 3. Table 3 shows a comparison of the observed and estimated values of some moments.
$ \sigma=0.35 $
, and divide each term by 4.5. By doing so we get a lognormal distribution which is approximated by a distribution with support on a finite interval (normalized to [0, 1]). The three-dimensional histogram constructed in this way and the fitted joint probability density function (using a BFSPH distribution of order 7) are shown in Figure 3. Table 3 shows a comparison of the observed and estimated values of some moments.
Table 2: Comparison of observed and estimated values of some moments of the BFSPH distribution with
![]() $ X\sim B(0.5,5)$
,
$ X\sim B(0.5,5)$
,
![]() $Y=0.3X+\varepsilon$
,
$Y=0.3X+\varepsilon$
,
![]() $\varepsilon \sim \frac{1}{25}{\rm Erlang}(2,1.5)$
.
$\varepsilon \sim \frac{1}{25}{\rm Erlang}(2,1.5)$
.


Figure 2:
Bivariate finite support vector (X, Y), where
![]() $ X \sim B(0.5,5) $
and
$ X \sim B(0.5,5) $
and
![]() $ Y=0.3X+\varepsilon$
,
$ Y=0.3X+\varepsilon$
,
![]() $\varepsilon \sim \dfrac{1}{25}{\rm Erlang}(2,1.5)$
, fitted with a BFSPH distribution of order 4.
$\varepsilon \sim \dfrac{1}{25}{\rm Erlang}(2,1.5)$
, fitted with a BFSPH distribution of order 4.
In the regression model considered above, if we take the coefficient of X to be a number close to 0.3,
![]() $ \varepsilon $
a uniform variate over (0, 1), and X a truncated beta or gamma variate, it can be seen that (X, Y) is fitted with a BFSPH distribution with a small number of phases, though Y is heavily influenced by the U(0, 1) variate, which requires [Reference Ramaswami and Viswanath8] a large number of phases for modelling. Perhaps, since the U(0, 1) variate comes up only as a term in a convolution, the fits appeared to have come out very well with a small number of phases. However, due to space restrictions, these illustrations are not graphically demonstrated here.
$ \varepsilon $
a uniform variate over (0, 1), and X a truncated beta or gamma variate, it can be seen that (X, Y) is fitted with a BFSPH distribution with a small number of phases, though Y is heavily influenced by the U(0, 1) variate, which requires [Reference Ramaswami and Viswanath8] a large number of phases for modelling. Perhaps, since the U(0, 1) variate comes up only as a term in a convolution, the fits appeared to have come out very well with a small number of phases. However, due to space restrictions, these illustrations are not graphically demonstrated here.
Table 3: Comparison of observed and estimated values of some moments of the BFSPH distribution with
![]() $X\sim {\rm normalized\ lognormal}(0.1,0.35)\ {\rm variate\ over}\ [0,1]$
,
$X\sim {\rm normalized\ lognormal}(0.1,0.35)\ {\rm variate\ over}\ [0,1]$
,
![]() $Y=5X+1+\varepsilon$
,
$Y=5X+1+\varepsilon$
,
![]() $\varepsilon \sim U({-}1,1)$
.
$\varepsilon \sim U({-}1,1)$
.


Figure 3:
Bivariate finite support vector (X, Y), X lognormal with parameters 0.1 and 0.35, normalized over [0, 1],
![]() $ Y=5X+1+\varepsilon$
,
$ Y=5X+1+\varepsilon$
,
![]() $\varepsilon \sim U({-}1,1) $
, fitted with a BFSPH distribution of order 7.
$\varepsilon \sim U({-}1,1) $
, fitted with a BFSPH distribution of order 7.
Appendix A. Derivation of the matrices
 $\beta_{+}^{*}$
and
$\beta_{+}^{*}$
and
 $T_{+}^{*}$
from
$T_{+}^{*}$
from
 $\pi$
and T
$\pi$
and T
Let P be the matrix defined as
 \begin{equation*} P_{ij}= \left\{ \begin{array}{c@{\quad}c} \frac{T_{ij}}{-T_{ii}} & {\rm if}\ i \neq j,\\ 0& {\rm if}\ i = j. \end{array} \right. \end{equation*}
\begin{equation*} P_{ij}= \left\{ \begin{array}{c@{\quad}c} \frac{T_{ij}}{-T_{ii}} & {\rm if}\ i \neq j,\\ 0& {\rm if}\ i = j. \end{array} \right. \end{equation*}
Now, partition the set of transient states into two sets,
![]() $ S_{+} $
and
$ S_{+} $
and
![]() $ S_{0} $
, according to the rate at which the reward is obtained when the process is at state i,
$ S_{0} $
, according to the rate at which the reward is obtained when the process is at state i,
![]() $1\leq i \leq p$
, as follows:
$1\leq i \leq p$
, as follows:
This assumption enables us to partition the matrices P and
![]() $ \pi $
over
$ \pi $
over
![]() $ S_{+} $
and
$ S_{+} $
and
![]() $ S_{0}$
, and we get
$ S_{0}$
, and we get
 \begin{equation*} P= \left ( \begin{array}{cc} P_{++}&\quad P_{+0}\\[5pt]
P_{0+}&\quad P_{00} \end{array} \right ), \qquad \pi = (\pi_{+},\pi_{0}), \end{equation*}
\begin{equation*} P= \left ( \begin{array}{cc} P_{++}&\quad P_{+0}\\[5pt]
P_{0+}&\quad P_{00} \end{array} \right ), \qquad \pi = (\pi_{+},\pi_{0}), \end{equation*}
where
![]() $ P_{++} $
corresponds to the transitions between the states in
$ P_{++} $
corresponds to the transitions between the states in
![]() $ S_{+} $
,
$ S_{+} $
,
![]() $ P_{+0} $
the transitions from
$ P_{+0} $
the transitions from
![]() $ S_{+} $
to
$ S_{+} $
to
![]() $ S_{0} $
,
$ S_{0} $
,
![]() $ P_{0+} $
the transitions from
$ P_{0+} $
the transitions from
![]() $ S_{0} $
to
$ S_{0} $
to
![]() $ S_{+} $
, and
$ S_{+} $
, and
![]() $ P_{00} $
the transitions between the states in
$ P_{00} $
the transitions between the states in
![]() $ S_{0} $
,
$ S_{0} $
,
![]() $ \pi_{+} $
is the initial probability vector for the states in
$ \pi_{+} $
is the initial probability vector for the states in
![]() $ S_{+}$
, and
$ S_{+}$
, and
![]() $ \pi_{0} $
is the initial probability vector for the states in
$ \pi_{0} $
is the initial probability vector for the states in
![]() $ S_{0} $
. Now, take
$ S_{0} $
. Now, take
![]() $P_{+}^{*} = P_{++} +P_{+0}(I-P_{00})^{-1}P_{0+}$
to define the vector
$P_{+}^{*} = P_{++} +P_{+0}(I-P_{00})^{-1}P_{0+}$
to define the vector
and the matrix
![]() $T_{+}^{*}$
, where
$T_{+}^{*}$
, where
 \begin{equation*} [T_{+}^{*}]_{ij}= \left \{ \begin{array}{cc} \frac{T_{ii}(1-[P_{+}^{*}]_{ii})}{r(i)}& \quad{\rm if}\ i =j,\\[6pt]
\frac{-T_{ii}[P_{+}^{*}]_{ij}}{r(i)}& \quad{\rm if}\ i \neq j. \end{array} \right. \end{equation*}
\begin{equation*} [T_{+}^{*}]_{ij}= \left \{ \begin{array}{cc} \frac{T_{ii}(1-[P_{+}^{*}]_{ii})}{r(i)}& \quad{\rm if}\ i =j,\\[6pt]
\frac{-T_{ii}[P_{+}^{*}]_{ij}}{r(i)}& \quad{\rm if}\ i \neq j. \end{array} \right. \end{equation*}
We can show that
![]() $ Y\sim {\rm PH}(\beta_{+}^{*},T_{+}^{*}) $
. For more details, see [Reference Kulkarni6].
$ Y\sim {\rm PH}(\beta_{+}^{*},T_{+}^{*}) $
. For more details, see [Reference Kulkarni6].
Appendix B. Estimation of sufficient statistics for BFSPH from those of BPH*
The estimates of the sufficient statistics for the BPH* distribution discussed in Section 4.1 (see also [Reference Esparza, Nielsen and Bladt5]) are
 \begin{equation} \hat{Z_{i}} = \left\{ \begin{array}{l@{\quad}l} \tilde{c}(x)\pi_{1}M(y_{1},\textbf{e}_{i},\textbf{e}_{i},T_{11})T_{12} {\rm e}^{T_{22}y_{2}}\textbf{t}_{2} , & \quad 1\leq i\leq p_{1}\kern-1pt ; \\[3pt] \tilde{c}(x)\pi_{1}{\rm e}^{T_{11}y_{1}}T_{12}M(y_{2},\textbf{e}_{i},\textbf{e}_{i},T_{22})\textbf{t}_{2} , & \quad p_{1}+1\leq i\leq p; \end{array} \right.\qquad\qquad\ \ \end{equation}
\begin{equation} \hat{Z_{i}} = \left\{ \begin{array}{l@{\quad}l} \tilde{c}(x)\pi_{1}M(y_{1},\textbf{e}_{i},\textbf{e}_{i},T_{11})T_{12} {\rm e}^{T_{22}y_{2}}\textbf{t}_{2} , & \quad 1\leq i\leq p_{1}\kern-1pt ; \\[3pt] \tilde{c}(x)\pi_{1}{\rm e}^{T_{11}y_{1}}T_{12}M(y_{2},\textbf{e}_{i},\textbf{e}_{i},T_{22})\textbf{t}_{2} , & \quad p_{1}+1\leq i\leq p; \end{array} \right.\qquad\qquad\ \ \end{equation}
 \begin{equation} \hat{N}_{ij} = \left\{ \begin{array}{l@{\quad\ \ }l} (T_{11})_{ij}\tilde{c}(x)\pi_{1}M(y_{1},\textbf{e}_{i},\textbf{e}_{j},T_{11})T_{12}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , & 1\leq i, j \leq p_{1}\kern-1pt ; \\[3pt] (T_{12})_{ij^{*}}\tilde{c}(x)\pi_{1}{\rm e}^{T_{11}y_{1}}\textbf{e}_{i}\textbf{e}_{j}^{\top}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , & 1\leq i\leq p_{1}\kern-1pt , \\[3pt] & p_{1}+1\leq j\leq p ; \\[3pt] (T_{22})_{i^{*}j^{*}}\tilde{c}(x)\pi_{1}{\rm e}^{T_{11}x_{1}}T_{12}M(y_{2},\textbf{e}_{i^{*}},\textbf{e}_{j^{*}},T_{22})\textbf{t}_{2} , & p_{1}+1\leq i , j \leq p, \\[3pt] \end{array} \right.\end{equation}
\begin{equation} \hat{N}_{ij} = \left\{ \begin{array}{l@{\quad\ \ }l} (T_{11})_{ij}\tilde{c}(x)\pi_{1}M(y_{1},\textbf{e}_{i},\textbf{e}_{j},T_{11})T_{12}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , & 1\leq i, j \leq p_{1}\kern-1pt ; \\[3pt] (T_{12})_{ij^{*}}\tilde{c}(x)\pi_{1}{\rm e}^{T_{11}y_{1}}\textbf{e}_{i}\textbf{e}_{j}^{\top}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , & 1\leq i\leq p_{1}\kern-1pt , \\[3pt] & p_{1}+1\leq j\leq p ; \\[3pt] (T_{22})_{i^{*}j^{*}}\tilde{c}(x)\pi_{1}{\rm e}^{T_{11}x_{1}}T_{12}M(y_{2},\textbf{e}_{i^{*}},\textbf{e}_{j^{*}},T_{22})\textbf{t}_{2} , & p_{1}+1\leq i , j \leq p, \\[3pt] \end{array} \right.\end{equation}
where
 \begin{align*} \tilde{a}(x) & = {\rm e}^{T_{11}x_{1}}T_{12}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , \\ \tilde{b}(x) & = \pi_{1}{\rm e}^{T_{11}x_{1}}T_{12}{\rm e}^{T_{22}x_{2}} , \\ \tilde{c}(x) & = \dfrac{1}{\pi_{1}\tilde{a}(x)}.\end{align*}
\begin{align*} \tilde{a}(x) & = {\rm e}^{T_{11}x_{1}}T_{12}{\rm e}^{T_{22}x_{2}}\textbf{t}_{2} , \\ \tilde{b}(x) & = \pi_{1}{\rm e}^{T_{11}x_{1}}T_{12}{\rm e}^{T_{22}x_{2}} , \\ \tilde{c}(x) & = \dfrac{1}{\pi_{1}\tilde{a}(x)}.\end{align*}
Corresponding to a single sample
![]() $ x=(x_{1},x_{2}) $
on a BFSPH
$ x=(x_{1},x_{2}) $
on a BFSPH
![]() $_{1}^{R}(\pi,T) $
variate, the observation
$_{1}^{R}(\pi,T) $
variate, the observation
![]() $y=x+n$
, for some
$y=x+n$
, for some
![]() $ n=(n_{1},n_{2})$
,
$ n=(n_{1},n_{2})$
,
![]() $n_{1},n_{2}\in \{0,1,2,3,\dots\}$
, and
$n_{1},n_{2}\in \{0,1,2,3,\dots\}$
, and
![]() $ y=(y_{1},y_{2}) $
, is a sample on the BPH
$ y=(y_{1},y_{2}) $
, is a sample on the BPH
![]() $^{*}(\pi, T) $
variate with reward matrix R. Then, to evaluate the conditional expectation given
$^{*}(\pi, T) $
variate with reward matrix R. Then, to evaluate the conditional expectation given
![]() $(x_{1},x_{2})$
by using the conditional expectations given both y and
$(x_{1},x_{2})$
by using the conditional expectations given both y and
![]() $ \lfloor y \rfloor $
, where
$ \lfloor y \rfloor $
, where
![]() $ \lfloor y \rfloor = (\lfloor y_{1}\rfloor, \lfloor y_{2}\rfloor)$
, we can use the function g defined by
$ \lfloor y \rfloor = (\lfloor y_{1}\rfloor, \lfloor y_{2}\rfloor)$
, we can use the function g defined by
 \begin{align}\notag g(n\mid x) & = \mathbb{P}(\lfloor Y \rfloor=n \mid X=x) \\
& = \dfrac{\pi_{1}{\rm e}^{T_{11}(x_{1}+n_{1})}T_{12}{\rm e}^{T_{22}(x_{2}+n_{2})}\textbf{t}_{2}}{\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-e^{T_{22}})^{-1}\textbf{t}_{2}}.\end{align}
\begin{align}\notag g(n\mid x) & = \mathbb{P}(\lfloor Y \rfloor=n \mid X=x) \\
& = \dfrac{\pi_{1}{\rm e}^{T_{11}(x_{1}+n_{1})}T_{12}{\rm e}^{T_{22}(x_{2}+n_{2})}\textbf{t}_{2}}{\pi_{1}{\rm e}^{T_{11}x_{1}}(I-{\rm e}^{T_{11}})^{-1}T_{12}{\rm e}^{T_{22}x_{2}}(I-e^{T_{22}})^{-1}\textbf{t}_{2}}.\end{align}
Now, (7)–(10) can be obtained by multiplying (18) with the corresponding terms in (14)–(17) and taking summation over
![]() $ n_{1} $
and
$ n_{1} $
and
![]() $ n_{2} $
.
$ n_{2} $
.
Acknowledgement
The authors thank the anonymous referee for their constructive comments and suggestions that improved the quality of the paper significantly.