We study the analogue of the Bombieri–Vinogradov theorem for 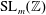 $\operatorname{SL}_{m}(\mathbb{Z})$ Hecke–Maass form
$\operatorname{SL}_{m}(\mathbb{Z})$ Hecke–Maass form  $F(z)$. In particular, for
$F(z)$. In particular, for 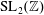 $\operatorname{SL}_{2}(\mathbb{Z})$ holomorphic or Maass Hecke eigenforms, symmetric-square lifts of holomorphic Hecke eigenforms on
$\operatorname{SL}_{2}(\mathbb{Z})$ holomorphic or Maass Hecke eigenforms, symmetric-square lifts of holomorphic Hecke eigenforms on 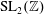 $\operatorname{SL}_{2}(\mathbb{Z})$, and
$\operatorname{SL}_{2}(\mathbb{Z})$, and 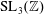 $\operatorname{SL}_{3}(\mathbb{Z})$ Maass Hecke eigenforms under the Ramanujan conjecture, the levels of distribution are all equal to
$\operatorname{SL}_{3}(\mathbb{Z})$ Maass Hecke eigenforms under the Ramanujan conjecture, the levels of distribution are all equal to 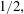 $1/2,$ which is as strong as the Bombieri–Vinogradov theorem. As an application, we study an automorphic version of Titchmarch’s divisor problem; namely for
$1/2,$ which is as strong as the Bombieri–Vinogradov theorem. As an application, we study an automorphic version of Titchmarch’s divisor problem; namely for  $a\neq 0,$
$a\neq 0,$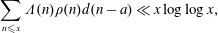 $$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D70C}(n)d(n-a)\ll x\log \log x,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D70C}(n)d(n-a)\ll x\log \log x,\end{eqnarray}$$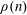 $\unicode[STIX]{x1D70C}(n)$ are Fourier coefficients
$\unicode[STIX]{x1D70C}(n)$ are Fourier coefficients 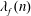 $\unicode[STIX]{x1D706}_{f}(n)$ of a holomorphic Hecke eigenform
$\unicode[STIX]{x1D706}_{f}(n)$ of a holomorphic Hecke eigenform 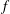 $f$ for
$f$ for 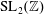 $\operatorname{SL}_{2}(\mathbb{Z})$ or Fourier coefficients
$\operatorname{SL}_{2}(\mathbb{Z})$ or Fourier coefficients 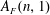 $A_{F}(n,1)$ of its symmetric-square lift
$A_{F}(n,1)$ of its symmetric-square lift 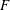 $F$. Further, as a consequence, we get an asymptotic formula
$F$. Further, as a consequence, we get an asymptotic formula 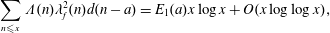 $$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D706}_{f}^{2}(n)d(n-a)=E_{1}(a)x\log x+O(x\log \log x),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D706}_{f}^{2}(n)d(n-a)=E_{1}(a)x\log x+O(x\log \log x),\end{eqnarray}$$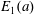 $E_{1}(a)$ is a constant depending on
$E_{1}(a)$ is a constant depending on  $a$. Moreover, we also consider the asymptotic orthogonality of the Möbius function against the arithmetic function
$a$. Moreover, we also consider the asymptotic orthogonality of the Möbius function against the arithmetic function 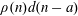 $\unicode[STIX]{x1D70C}(n)d(n-a)$.
$\unicode[STIX]{x1D70C}(n)d(n-a)$.