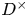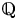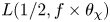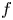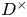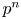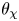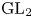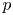1. Introduction
Let ![]() $D$ be an indefinite quaternion algebra over
$D$ be an indefinite quaternion algebra over ![]() ${\mathbb {Q}}$. For any integer
${\mathbb {Q}}$. For any integer ![]() $N$ coprime to the discriminant of
$N$ coprime to the discriminant of ![]() $D$, let
$D$, let ![]() $\Gamma ^D_0(N)\subset \textrm {SL}_2({\mathbb {R}})$ denote the congruence subgroupFootnote 1 corresponding to the norm 1 units of an Eichler order of level
$\Gamma ^D_0(N)\subset \textrm {SL}_2({\mathbb {R}})$ denote the congruence subgroupFootnote 1 corresponding to the norm 1 units of an Eichler order of level ![]() $N$ inside
$N$ inside ![]() $D$. There has been a lot of work on bounding the sup-norm
$D$. There has been a lot of work on bounding the sup-norm ![]() $\|f \|_\infty$ of a Hecke–Maass newform of weight 0 and Laplace eigenvalue
$\|f \|_\infty$ of a Hecke–Maass newform of weight 0 and Laplace eigenvalue ![]() $\lambda$ on
$\lambda$ on ![]() $\Gamma ^D_0(N) \backslash \mathbb {H}$, where
$\Gamma ^D_0(N) \backslash \mathbb {H}$, where ![]() $f$ is
$f$ is ![]() $L^2$-normalized with respect to the measure that gives volume 1 to
$L^2$-normalized with respect to the measure that gives volume 1 to ![]() $\Gamma ^D_0(N) \backslash \mathbb {H}$. (For simplicity, we only discuss the case of newforms with trivial character in the introduction.)
$\Gamma ^D_0(N) \backslash \mathbb {H}$. (For simplicity, we only discuss the case of newforms with trivial character in the introduction.)
The pioneering work here is due to Iwaniec and Sarnak [Reference Iwaniec and SarnakIS95], who proved the eigenvalue aspect boundFootnote 2 ![]() $\|f\|_\infty \ll _\epsilon \lambda ^{5/24 + \epsilon }$ in the case
$\|f\|_\infty \ll _\epsilon \lambda ^{5/24 + \epsilon }$ in the case ![]() $N=1$. For the level-aspect analogue of this problem, the goal is to bound
$N=1$. For the level-aspect analogue of this problem, the goal is to bound ![]() $\|f\|_\infty$ in terms of
$\|f\|_\infty$ in terms of ![]() $N$, with the dependence on
$N$, with the dependence on ![]() $\lambda$ suppressed. It will be convenient to use the notation
$\lambda$ suppressed. It will be convenient to use the notation ![]() $N_1$ to denote the smallest integer such that
$N_1$ to denote the smallest integer such that ![]() $N|N_1^2$. Clearly,
$N|N_1^2$. Clearly, ![]() $\sqrt {N} \leqslant N_1 \leqslant N$. Note that
$\sqrt {N} \leqslant N_1 \leqslant N$. Note that ![]() $N_1$ equals
$N_1$ equals ![]() $N$ if
$N$ if ![]() $N$ is squarefree while
$N$ is squarefree while ![]() $N_1$ is around
$N_1$ is around ![]() $\sqrt {N}$ when all the prime factors of
$\sqrt {N}$ when all the prime factors of ![]() $N$ divide it to a high power. To show the rapid progress in the level-aspect version of the sup-norm problem for newforms on
$N$ divide it to a high power. To show the rapid progress in the level-aspect version of the sup-norm problem for newforms on ![]() $D$, we quote the results proved so far in this direction.Footnote 3
$D$, we quote the results proved so far in this direction.Footnote 3
1.0.1 The case  $D = M_2({\mathbb {Q}})$
$D = M_2({\mathbb {Q}})$
The ‘trivial bound’ (which is not completely trivial, since one has to be careful about behaviour near cusps) is ![]() $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2+ \epsilon }$. The following bounds were proved in rapid succession:
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2+ \epsilon }$. The following bounds were proved in rapid succession:
–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2 -{25}/{914} + \epsilon }$ for squarefree
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2 -{25}/{914} + \epsilon }$ for squarefree  $N$ (Blomer and Holowinsky [Reference Blomer and HolowinskyBH10], 2010);
$N$ (Blomer and Holowinsky [Reference Blomer and HolowinskyBH10], 2010);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{22} + \epsilon }$ for squarefree
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{22} + \epsilon }$ for squarefree  $N$ (Templier [Reference TemplierTem10], 2010);
$N$ (Templier [Reference TemplierTem10], 2010);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{20} + \epsilon }$ for squarefree
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{20} + \epsilon }$ for squarefree  $N$ (Helfgott and Ricotta, unpublished);
$N$ (Helfgott and Ricotta, unpublished);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{12} + \epsilon }$ for squarefree
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{12} + \epsilon }$ for squarefree  $N$ (Harcos and Templier [Reference Harcos and TemplierHT12], 2012);
$N$ (Harcos and Templier [Reference Harcos and TemplierHT12], 2012);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{{1}/{3} + \epsilon }$ for squarefree
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{{1}/{3} + \epsilon }$ for squarefree  $N$ (Harcos and Templier [Reference Harcos and TemplierHT13], 2013);
$N$ (Harcos and Templier [Reference Harcos and TemplierHT13], 2013);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/6 + \epsilon } N_1^{1/6}$ for general
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/6 + \epsilon } N_1^{1/6}$ for general  $N$ (Saha [Reference SahaSah17], 2017).
$N$ (Saha [Reference SahaSah17], 2017).
1.0.2 The case  $D$ a division algebra
$D$ a division algebra
The ‘trivial bound’ is again ![]() $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2+ \epsilon }$. The following improved bounds have been proved so far:
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2+ \epsilon }$. The following improved bounds have been proved so far:
–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{24} + \epsilon }$ for general
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{1/2-{1}/{24} + \epsilon }$ for general  $N$ (Templier [Reference TemplierTem10], 2010);
$N$ (Templier [Reference TemplierTem10], 2010);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N_1^{1/2+\epsilon }$ for general
$\|f\|_\infty \ll _{\lambda , \epsilon } N_1^{1/2+\epsilon }$ for general  $N$ (Marshall [Reference MarshallMar16], 2016);
$N$ (Marshall [Reference MarshallMar16], 2016);–
 $\|f\|_\infty \ll _{\lambda , \epsilon } N^{{1}/{24}+\epsilon }N_1^{1/2 - {1}/{12}}$ for general
$\|f\|_\infty \ll _{\lambda , \epsilon } N^{{1}/{24}+\epsilon }N_1^{1/2 - {1}/{12}}$ for general  $N$ (Saha [Reference SahaSah20], 2020).
$N$ (Saha [Reference SahaSah20], 2020).
Our main focus in this paper is on a natural subcase of the level aspect, known as the depth aspect, where one takes ![]() $N=p^n$ with
$N=p^n$ with ![]() $p$ a fixed prime and
$p$ a fixed prime and ![]() $n$ varying. In this aspect, the best currently known bound for the sup-norm is
$n$ varying. In this aspect, the best currently known bound for the sup-norm is
as is clear from the list of previous results above; indeed, the bound (1) in the case ![]() $D=M_2({\mathbb {Q}})$ follows from work of the second-named author [Reference SahaSah17] and in the case when
$D=M_2({\mathbb {Q}})$ follows from work of the second-named author [Reference SahaSah17] and in the case when ![]() $D$ is a division algebra it follows from work of Marshall [Reference MarshallMar16]. More pertinently, the bound (1) coincides with the level-aspect local bound (which is stronger than the trivial boundFootnote 4), which states in general that
$D$ is a division algebra it follows from work of Marshall [Reference MarshallMar16]. More pertinently, the bound (1) coincides with the level-aspect local bound (which is stronger than the trivial boundFootnote 4), which states in general that
When we restrict ourselves to the depth aspect, we have ![]() $N_1 \asymp \sqrt {N}$ as
$N_1 \asymp \sqrt {N}$ as ![]() $N=p^n \rightarrow \infty$ and so (1) is essentially equivalent to (2) in this aspect. In contrast, for squarefree levels
$N=p^n \rightarrow \infty$ and so (1) is essentially equivalent to (2) in this aspect. In contrast, for squarefree levels ![]() $N$, we have
$N$, we have ![]() $N_1=N$, and the best currently known bounds in that case, due to Harcos and Templier [Reference Harcos and TemplierHT13] for
$N_1=N$, and the best currently known bounds in that case, due to Harcos and Templier [Reference Harcos and TemplierHT13] for ![]() $D=M_2({\mathbb {Q}})$ and Templier [Reference TemplierTem10] for
$D=M_2({\mathbb {Q}})$ and Templier [Reference TemplierTem10] for ![]() $D$ a division algebra, successfully beat the local bound by a positive power of
$D$ a division algebra, successfully beat the local bound by a positive power of ![]() $N$, as evidenced from the list of previous results quoted earlier. However, despite considerable recent activity on the sup-norm problem, the local bound in the depth aspect for newforms has not been improved upon so far. We refer the reader to the end of the introduction of [Reference SahaSah20] for a brief discussion of why the usual methods are not sufficient to beat the local bound in this case.
$N$, as evidenced from the list of previous results quoted earlier. However, despite considerable recent activity on the sup-norm problem, the local bound in the depth aspect for newforms has not been improved upon so far. We refer the reader to the end of the introduction of [Reference SahaSah20] for a brief discussion of why the usual methods are not sufficient to beat the local bound in this case.
In this paper, we improve upon (1) for the first time. For this, we introduce a new technique to attack the sup-norm problem which relies on quantifying the decay of local matrix coefficients at the ramified primes along a filtration of compact subsets. To avoid dealing with behaviour at the cusps and Whittaker expansions, we restrict ourselves here to the case of ![]() $D$ a division algebra (though we have no doubt that our results can be extended to the case of
$D$ a division algebra (though we have no doubt that our results can be extended to the case of ![]() $\textrm {GL}_2$ with some additional technical work). We prove the following result.
$\textrm {GL}_2$ with some additional technical work). We prove the following result.
Theorem A (See Corollary 4.9) Let ![]() $D$ be a fixed indefinite quaternion division algebra over
$D$ be a fixed indefinite quaternion division algebra over ![]() ${\mathbb {Q}}$ and
${\mathbb {Q}}$ and ![]() $p$ be an odd prime coprime to the discriminant of
$p$ be an odd prime coprime to the discriminant of ![]() $D$. Then, for any
$D$. Then, for any ![]() $L^2$-normalized Maass newform
$L^2$-normalized Maass newform ![]() $f$ of Laplace eigenvalue
$f$ of Laplace eigenvalue ![]() $\lambda$ on
$\lambda$ on ![]() $\Gamma ^D_0(p^n) \backslash \mathbb {H}$, we have
$\Gamma ^D_0(p^n) \backslash \mathbb {H}$, we have
Remark 1.1 Corollary 4.9 of this paper is more general than Theorem A in that it allows for general composite levels (and the implied constant is polynomial in the product of primes dividing the level). Corollary 4.9 also includes the case of holomorphic forms ![]() $f$. Corollary 4.9 is itself a very special case of the master theorem of this paper, Theorem 4.6, which applies to any family of automorphic forms on
$f$. Corollary 4.9 is itself a very special case of the master theorem of this paper, Theorem 4.6, which applies to any family of automorphic forms on ![]() $D^\times ({\mathbb {A}})$ satisfying certain hypotheses on decay of matrix coefficients.
$D^\times ({\mathbb {A}})$ satisfying certain hypotheses on decay of matrix coefficients.
We will explain the main ideas behind the proof of Theorem A later in this introduction, but, first, let us describe an interesting application of this theorem to the subconvexity problem for central ![]() $L$-values. The key idea, going back to Sarnak (see the nice exposition in § 4 of [Reference SarnakSar93]), is that the conjectured strongest bounds for the sup-norms of automorphic forms often imply the Lindelöf hypothesis in certain aspects for their associated
$L$-values. The key idea, going back to Sarnak (see the nice exposition in § 4 of [Reference SarnakSar93]), is that the conjectured strongest bounds for the sup-norms of automorphic forms often imply the Lindelöf hypothesis in certain aspects for their associated ![]() $L$-functions. This leads to the question of whether one can use non-trivial sup-norm bounds to deduce subconvexity bounds for
$L$-functions. This leads to the question of whether one can use non-trivial sup-norm bounds to deduce subconvexity bounds for ![]() $L$-functions. In this context, Iwaniec and Sarnak pointed out (see Remark D of [Reference Iwaniec and SarnakIS95]) that their sup-norm result leads via Eisenstein series to a
$L$-functions. In this context, Iwaniec and Sarnak pointed out (see Remark D of [Reference Iwaniec and SarnakIS95]) that their sup-norm result leads via Eisenstein series to a ![]() $t$-aspect subconvexity result for the Riemann zeta function. In fact, sup-norm bounds for Eisenstein series proved in [Reference YoungYou18] and [Reference BlomerBlo18] directly imply subconvexity bounds in the
$t$-aspect subconvexity result for the Riemann zeta function. In fact, sup-norm bounds for Eisenstein series proved in [Reference YoungYou18] and [Reference BlomerBlo18] directly imply subconvexity bounds in the ![]() $t$-aspect for the Dedekind
$t$-aspect for the Dedekind ![]() $L$-functions of imaginary quadratic fields (this follows by considering the values taken by the Eisenstein series at CM points). Very recently, uniform sup-norm bounds (with a dependence on the point of evaluation) have been used in [Reference NordentoftNor20] to prove hybrid subconvexity bounds in the
$L$-functions of imaginary quadratic fields (this follows by considering the values taken by the Eisenstein series at CM points). Very recently, uniform sup-norm bounds (with a dependence on the point of evaluation) have been used in [Reference NordentoftNor20] to prove hybrid subconvexity bounds in the ![]() $t$ and
$t$ and ![]() $m$ aspects for
$m$ aspects for ![]() $L$-functions of ideal class characters of quadratic fields of discriminant
$L$-functions of ideal class characters of quadratic fields of discriminant ![]() $m$.
$m$.
However, the above-mentioned subconvexity results are only for ![]() $\textrm {GL}_1$
$\textrm {GL}_1$ ![]() $L$-functions and use sup-norm bounds in the eigenvalue aspect. Regarding the level-aspect sup-norm problem for cusp forms on the upper-half plane and its connection to the subconvexity problem, see the discussion on page 647 of [Reference Blomer and HolowinskyBH10], which points out that to prove any level-aspect subconvexity bound for an associated
$L$-functions and use sup-norm bounds in the eigenvalue aspect. Regarding the level-aspect sup-norm problem for cusp forms on the upper-half plane and its connection to the subconvexity problem, see the discussion on page 647 of [Reference Blomer and HolowinskyBH10], which points out that to prove any level-aspect subconvexity bound for an associated ![]() $L$-function by directly substituting a sup-norm bound into a period formula typically requires very strongFootnote 5 sup-norm bounds. In particular, for level-aspect subconvexity, one needs to beat the exponent
$L$-function by directly substituting a sup-norm bound into a period formula typically requires very strongFootnote 5 sup-norm bounds. In particular, for level-aspect subconvexity, one needs to beat the exponent ![]() $1/4$ for the sup-norm problem. Theorem A represents the first result that achieves this. Therefore, in this paper, we are finally able to carry out this strategy to deduce a depth-aspect subconvexity bound from Theorem A. We give below a special case of the result we are able to obtain.
$1/4$ for the sup-norm problem. Theorem A represents the first result that achieves this. Therefore, in this paper, we are finally able to carry out this strategy to deduce a depth-aspect subconvexity bound from Theorem A. We give below a special case of the result we are able to obtain.
Theorem B (see Theorem 6.2, Corollaries 6.3 and 6.6)
Let ![]() $D$ be a fixed indefinite quaternion division algebra over
$D$ be a fixed indefinite quaternion division algebra over ![]() ${\mathbb {Q}}$ and let
${\mathbb {Q}}$ and let ![]() $p$ be an odd prime coprime to the discriminant of
$p$ be an odd prime coprime to the discriminant of ![]() $D$. Let
$D$. Let ![]() $K$ be a quadratic number field such that
$K$ be a quadratic number field such that ![]() $p$ splits in
$p$ splits in ![]() $K$ and all primes dividing the discriminant of
$K$ and all primes dividing the discriminant of ![]() $D$ are inert in
$D$ are inert in ![]() $K$. Let
$K$. Let ![]() $\chi$ be a Hecke character of
$\chi$ be a Hecke character of ![]() $K$ such that
$K$ such that ![]() $\chi |_{{\mathbb {A}}^\times } = 1$ and such that the ramification set of
$\chi |_{{\mathbb {A}}^\times } = 1$ and such that the ramification set of ![]() $\chi$ does not intersect the places above
$\chi$ does not intersect the places above ![]() $\textrm {disc}(D)$. Let
$\textrm {disc}(D)$. Let ![]() $\theta _\chi$ be the automorphic formFootnote 6 on
$\theta _\chi$ be the automorphic formFootnote 6 on ![]() ${\rm GL}_2$ obtained as the theta lift of
${\rm GL}_2$ obtained as the theta lift of ![]() $\chi$. Let
$\chi$. Let ![]() $f$ be a Maass newform of Laplace eigenvalue
$f$ be a Maass newform of Laplace eigenvalue ![]() $\lambda$ on
$\lambda$ on ![]() $\Gamma ^D_0(p^n) \backslash \mathbb {H}$. Then
$\Gamma ^D_0(p^n) \backslash \mathbb {H}$. Then
where ![]() $L(s, f \times \theta _\chi )$ denotes the Rankin–Selberg
$L(s, f \times \theta _\chi )$ denotes the Rankin–Selberg ![]() $L$-function normalized to have functional equation
$L$-function normalized to have functional equation ![]() $s \mapsto 1-s$, and
$s \mapsto 1-s$, and ![]() $C(f \times \theta _\chi ) \asymp _\chi p^{2n}$ denotes the (finite part of the) conductor of
$C(f \times \theta _\chi ) \asymp _\chi p^{2n}$ denotes the (finite part of the) conductor of ![]() $L(s, f \times \theta _\chi )$.
$L(s, f \times \theta _\chi )$.
Remark 1.2 The classical construction of the theta lift ![]() $\theta _\chi$ goes back to Hecke and Maass. This was generalized in the representation-theoretic language by Shalika and Tanaka [Reference Shalika and TanakaST69]; see also [Reference Harris and KudlaHK91, § 13] for a more modern treatment. For an explicit formula for
$\theta _\chi$ goes back to Hecke and Maass. This was generalized in the representation-theoretic language by Shalika and Tanaka [Reference Shalika and TanakaST69]; see also [Reference Harris and KudlaHK91, § 13] for a more modern treatment. For an explicit formula for ![]() $\theta _\chi$ under certain assumptions, see also page 61 of [Reference Iwaniec and KowalskiIK04] for the holomorphic case and Appendix A.1 of [Reference Humphries and KhanHK20] for the Maass case. The automorphic representation corresponding to
$\theta _\chi$ under certain assumptions, see also page 61 of [Reference Iwaniec and KowalskiIK04] for the holomorphic case and Appendix A.1 of [Reference Humphries and KhanHK20] for the Maass case. The automorphic representation corresponding to ![]() $\theta _\chi$ is precisely the global automorphic induction
$\theta _\chi$ is precisely the global automorphic induction ![]() ${\mathcal {AI}}(\chi )$ of
${\mathcal {AI}}(\chi )$ of ![]() $\chi$ from
$\chi$ from ![]() ${\mathbb {A}}_K^\times$ to
${\mathbb {A}}_K^\times$ to ![]() $\textrm {GL}_2({\mathbb {A}})$. This is a special instance of the Langlands correspondence, as explained nicely in Gelbart's book [Reference GelbartGel75, 7.B].
$\textrm {GL}_2({\mathbb {A}})$. This is a special instance of the Langlands correspondence, as explained nicely in Gelbart's book [Reference GelbartGel75, 7.B].
Remark 1.3 Thanks to the Jacquet–Langlands correspondence, we may equivalently take ![]() $f$ in Theorem B to be a newform on
$f$ in Theorem B to be a newform on ![]() $\textrm {GL}_2$ (of level equal to
$\textrm {GL}_2$ (of level equal to ![]() $\textrm {disc}(D)p^n$). Theorem B may be viewed as a (depth-aspect) subconvexity result for
$\textrm {disc}(D)p^n$). Theorem B may be viewed as a (depth-aspect) subconvexity result for ![]() $L(1/2, f \times g)$, where
$L(1/2, f \times g)$, where ![]() $g= \theta _\chi$ is fixed and
$g= \theta _\chi$ is fixed and ![]() $f$ varies. Subconvexity for the Rankin–Selberg
$f$ varies. Subconvexity for the Rankin–Selberg ![]() $L$-function on
$L$-function on ![]() $\textrm {GL}_2 \times \textrm {GL}_2$ (with one of the
$\textrm {GL}_2 \times \textrm {GL}_2$ (with one of the ![]() $\textrm {GL}_2$ forms fixed) in the level aspect was first approached by Kowalski et al. [Reference Kowalski, Michel and VanderKamKMV02] and a complete solution was obtained by Harcos and Michel [Reference Harcos and MichelHM06]. Uniform subconvexity in all aspects was subsequently proved in ground-breaking work of Michel and Venkatesh [Reference Michel and VenkateshMV10], who showed that
$\textrm {GL}_2$ forms fixed) in the level aspect was first approached by Kowalski et al. [Reference Kowalski, Michel and VanderKamKMV02] and a complete solution was obtained by Harcos and Michel [Reference Harcos and MichelHM06]. Uniform subconvexity in all aspects was subsequently proved in ground-breaking work of Michel and Venkatesh [Reference Michel and VenkateshMV10], who showed that ![]() $L(1/2, f \times g) \ll _{g, \epsilon } C(f\times g)^{1/4 - \delta }$ for general
$L(1/2, f \times g) \ll _{g, \epsilon } C(f\times g)^{1/4 - \delta }$ for general ![]() $f$ and
$f$ and ![]() $g$ and some
$g$ and some ![]() $\delta >0$. There have also been recent works, notably by Wu, that make the (unspecified) exponent
$\delta >0$. There have also been recent works, notably by Wu, that make the (unspecified) exponent ![]() $\delta$ of Michel and Venkatesh explicit in various cases. We also remark that
$\delta$ of Michel and Venkatesh explicit in various cases. We also remark that
where ![]() $f_K$ denotes the base change of
$f_K$ denotes the base change of ![]() $f$ to
$f$ to ![]() $K$; so Theorem B may also be viewed as a special instance of subconvexity on
$K$; so Theorem B may also be viewed as a special instance of subconvexity on ![]() $\textrm {GL}_2({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$ with the character on
$\textrm {GL}_2({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$ with the character on ![]() $\textrm {GL}_1({\mathbb {A}}_K)$ fixed. We further note that in the special case that
$\textrm {GL}_1({\mathbb {A}}_K)$ fixed. We further note that in the special case that ![]() $\chi = \mathbf {1}$ is trivial, the
$\chi = \mathbf {1}$ is trivial, the ![]() $L$-function factors as
$L$-function factors as ![]() $L(1/2, f \times \theta _\mathbf {1}) = L(1/2, f \times \rho _K) L(1/2, f)$, where
$L(1/2, f \times \theta _\mathbf {1}) = L(1/2, f \times \rho _K) L(1/2, f)$, where ![]() $\rho _K$ is the quadratic Dirichlet character associated to
$\rho _K$ is the quadratic Dirichlet character associated to ![]() $K$.
$K$.
As the above discussion makes clear, subconvexity in the setup of Theorem B is not new. However, the exponent ![]() $5/24$ (corresponding to
$5/24$ (corresponding to ![]() $\delta = 1/24$) we obtain appears to be the current strongest bound in this particular setting. As a point of comparison, the exponent that can be extracted in our setting from the general bound given in Corollary 1.6 of [Reference Wu and AndersenWA18], followed by an application of (3), corresponds to
$\delta = 1/24$) we obtain appears to be the current strongest bound in this particular setting. As a point of comparison, the exponent that can be extracted in our setting from the general bound given in Corollary 1.6 of [Reference Wu and AndersenWA18], followed by an application of (3), corresponds to ![]() $\delta = ({1-2\theta })/{32} < {1}/{24}$.
$\delta = ({1-2\theta })/{32} < {1}/{24}$.
The proof of Theorem B uses an explicit version of Waldspurger's famous formula [Reference WaldspurgerWal85] relating squares of toric periods and central ![]() $L$-values. We emphasize that the proof follows immediately upon substituting the bound from Theorem A into this formula and does not need any additional ingredients.
$L$-values. We emphasize that the proof follows immediately upon substituting the bound from Theorem A into this formula and does not need any additional ingredients.
We now explain the main ideas behind Theorem A and how they can be put into a general framework. The usual strategyFootnote 7 to prove a sup-norm bound in the level aspect is to use the amplification method. This involves choosing a suitable global test function (a product of local test functions over all places) and then estimating the geometric side of the resulting pre-trace formula by counting the number of lattice points that lie in the support of the test function, as the level varies. This strategy successfully works to beat the local bound in the squarefree level aspect, where one can choose the local test functions at the ramified primes to be the indicator function (modulo the centre) of the local Hecke congruence subgroups. This strategy also works very well for families of automorphic forms corresponding to highly localized vectors at the ramified places, such as the minimal vectors or the ![]() $p$-adic microlocal lifts; the corresponding sup-norm bounds in these cases were proved in [Reference SahaSah20].
$p$-adic microlocal lifts; the corresponding sup-norm bounds in these cases were proved in [Reference SahaSah20].
Unfortunately, this strategy on its own fails to beat the local bound in the depth aspect for newforms. The reason is that local newvectors are not sufficiently localized in the depth aspect and consequently the support of the ‘best’ test function modulo the centre, as far as the depth aspect is concerned, is essentially the entire maximal compact subgroup. Therefore, the support does not involve many congruence conditions, and congruences are essential for achieving saving via counting. If we were to reduce the support of our ramified test functions further and thus force new congruences, the resulting saving via counting would be eclipsed by the resulting loss due to the fact that we will be averaging over more cusp forms.
The key new contribution of this paper is that we focus not merely on the support of the test function, but instead quantify how fast the test function (which is essentially the matrix coefficient of the local newvector) decays within the support. Roughly speaking, our method divides up the geometric side of the (amplified) pre-trace formula into multiple pieces, corresponding to a filtration of the support of the local test function. These pieces are estimated separately to obtain a general theorem that gives a sup-norm bound in the level aspect which is stronger than what can be obtained by existing methods. To illustrate our technique in the setting of Theorem A, for each level ![]() $N=p^n$ consider the filtration of compact subgroups
$N=p^n$ consider the filtration of compact subgroups ![]() $K^*(j) \subset K^*(j-1) \subset \cdots \subset K^*(1)$ of
$K^*(j) \subset K^*(j-1) \subset \cdots \subset K^*(1)$ of ![]() $\textrm {GL}_2({\mathbb {Z}}_p)$, where
$\textrm {GL}_2({\mathbb {Z}}_p)$, where ![]() $j \asymp n/8$ and
$j \asymp n/8$ and ![]() $K^*(i)$ is equal to the subgroup that looks like
$K^*(i)$ is equal to the subgroup that looks like ![]() $\big (\begin {smallmatrix}\ast & 0\\ 0 & \ast \end {smallmatrix}\big )$ modulo
$\big (\begin {smallmatrix}\ast & 0\\ 0 & \ast \end {smallmatrix}\big )$ modulo ![]() $p^i$. The support of the test function at the prime
$p^i$. The support of the test function at the prime ![]() $p$ is
$p$ is ![]() $K^*(1)$. We break up the geometric side of the pre-trace formula into
$K^*(1)$. We break up the geometric side of the pre-trace formula into ![]() $j$ pieces, with piece
$j$ pieces, with piece ![]() $i$ (for
$i$ (for ![]() $1 \leqslant i \leqslant j$) corresponding to the matrices whose local component at
$1 \leqslant i \leqslant j$) corresponding to the matrices whose local component at ![]() $p$ lies in
$p$ lies in ![]() $K^*(i)$ but not in
$K^*(i)$ but not in ![]() $K^*(i+1)$ (where we let
$K^*(i+1)$ (where we let ![]() $K^*(j+1)$ denote the empty set). Now we prove that these local matrix coefficients have a proper decay property, due to which the size of the test function at each matrix in piece
$K^*(j+1)$ denote the empty set). Now we prove that these local matrix coefficients have a proper decay property, due to which the size of the test function at each matrix in piece ![]() $i$ is boundedFootnote 8 by
$i$ is boundedFootnote 8 by ![]() $p^{{i}/{2} - {n}/{4}}$. Therefore, for each piece, we get a saving from two sources: (a) from the size of the test function, (b) from counting lattice points. The saving from source (a) is large when
$p^{{i}/{2} - {n}/{4}}$. Therefore, for each piece, we get a saving from two sources: (a) from the size of the test function, (b) from counting lattice points. The saving from source (a) is large when ![]() $i$ is small, which is precisely when the saving from source (b) is small. Conversely, when
$i$ is small, which is precisely when the saving from source (b) is small. Conversely, when ![]() $i$ is large, the saving from source (a) is small and the saving from source (b) is large. We emphasize that we are still using an amplified pre-trace formula, but with the extra ingredient described above, which leads to the bound in Theorem A.
$i$ is large, the saving from source (a) is small and the saving from source (b) is large. We emphasize that we are still using an amplified pre-trace formula, but with the extra ingredient described above, which leads to the bound in Theorem A.
The reader may have noticed that our exponent ![]() $5/24$ in Theorem A coincides with the exponent obtained by Iwaniec and Sarnak in [Reference Iwaniec and SarnakIS95]. In hindsight, our filtration strategy at a place
$5/24$ in Theorem A coincides with the exponent obtained by Iwaniec and Sarnak in [Reference Iwaniec and SarnakIS95]. In hindsight, our filtration strategy at a place ![]() $p$ is analogous to the argument used by Iwaniec and Sarnak in [Reference Iwaniec and SarnakIS95, Lemmas 1.1–1.3] for the test function at infinity in their classic work on the eigenvalue aspect of the sup-norm problem. Crucially, our bound for the size of
$p$ is analogous to the argument used by Iwaniec and Sarnak in [Reference Iwaniec and SarnakIS95, Lemmas 1.1–1.3] for the test function at infinity in their classic work on the eigenvalue aspect of the sup-norm problem. Crucially, our bound for the size of ![]() $p$-adic matrix coefficients, and that of Iwaniec and Sarnak for the archimedean matrix coefficient, both involve showing that the coefficient decays away from a torus. The relation between the sup-norm problem and subconvexity is also similar. In particular, when
$p$-adic matrix coefficients, and that of Iwaniec and Sarnak for the archimedean matrix coefficient, both involve showing that the coefficient decays away from a torus. The relation between the sup-norm problem and subconvexity is also similar. In particular, when ![]() $\chi$ is fixed in Theorem B, the local bound agrees with the convexity bound for the central
$\chi$ is fixed in Theorem B, the local bound agrees with the convexity bound for the central ![]() $L$-value, and the automorphic period we consider is a sum over a fixed collection of points if
$L$-value, and the automorphic period we consider is a sum over a fixed collection of points if ![]() $K$ is imaginary (respectively, a sum of integrals over closed geodesics if
$K$ is imaginary (respectively, a sum of integrals over closed geodesics if ![]() $K$ is real), and subconvexity follows from any improvement over the local bound with no cancellation in the sum being required. This is analogous to what happens on applying the Iwaniec–Sarnak bound for Eisenstein series, where one obtains a
$K$ is real), and subconvexity follows from any improvement over the local bound with no cancellation in the sum being required. This is analogous to what happens on applying the Iwaniec–Sarnak bound for Eisenstein series, where one obtains a ![]() $t$-aspect subconvexity result for the Riemann zeta function (see Remark D of [Reference Iwaniec and SarnakIS95]).
$t$-aspect subconvexity result for the Riemann zeta function (see Remark D of [Reference Iwaniec and SarnakIS95]).
On the other hand, the required bounds for the archimedean matrix coefficient used by Iwaniec and Sarnak (see Lemma 1.1 of [Reference Iwaniec and SarnakIS95]) follow in an elementary manner using integration by parts. However, our ![]() $p$-adic matrix coefficient is more subtle and so we need quantitative results on the decay across a sequence of compact subsets of matrix coefficients associated to local newvectors. Such results do not appear to be available in the literature; indeed, existing results on decay of matrix coefficients (see, e.g., [Reference OhOh02]) typically give the decay for the torus component of the elements (in the sense of the Cartan decomposition) going to infinity, which are completely orthogonal to what we require. In Theorem 5.4(1), we provide a general quantitative statement about the decay of these matrix coefficients of the sort we need, which may be of independent interest. The proof of Theorem 5.4 is carried out in § 5 (which can be read independently of the rest of the paper) and uses the stationary phase method in the
$p$-adic matrix coefficient is more subtle and so we need quantitative results on the decay across a sequence of compact subsets of matrix coefficients associated to local newvectors. Such results do not appear to be available in the literature; indeed, existing results on decay of matrix coefficients (see, e.g., [Reference OhOh02]) typically give the decay for the torus component of the elements (in the sense of the Cartan decomposition) going to infinity, which are completely orthogonal to what we require. In Theorem 5.4(1), we provide a general quantitative statement about the decay of these matrix coefficients of the sort we need, which may be of independent interest. The proof of Theorem 5.4 is carried out in § 5 (which can be read independently of the rest of the paper) and uses the stationary phase method in the ![]() $p$-adic context. A key role in the proof is played by a useful formulaFootnote 9 for the Whittaker newvector in terms of a family of
$p$-adic context. A key role in the proof is played by a useful formulaFootnote 9 for the Whittaker newvector in terms of a family of ![]() ${}_2F_1$ hypergeometric integrals, which allows us to use the
${}_2F_1$ hypergeometric integrals, which allows us to use the ![]() $p$-adic stationary phase method.
$p$-adic stationary phase method.
The idea outlined above can be phrased in a more general context (without any need to restrict ourselves to newforms) to prove an improved sup-norm bound whenever suitable results on decay of local matrix coefficients along a filtration of compact subsets are available. We develop a suitable language for such a result in §§ 3 and 4.1 leading to Theorem 4.6, which may be regarded as the ‘master theorem’ of this paper. Theorem 4.6 gives a strong sup-norm bound for any family of automorphic forms of powerful levels for which certain local hypotheses are satisfied. Thus, it reduces the question of proving these bounds to checking these local hypotheses, and Theorem 5.4, described earlier, is essentially the statement that these local hypotheses are satisfied by the family of local newvectors of odd conductor and trivial central character. The proof of Theorem 4.6 is carried out in § 4.3 and uses as a main ingredient a lattice-point counting result proved in [Reference SahaSah20].
We end this introduction with a few remarks about possible extensions of this work. It should be possible to extend the argument to prove a non-trivial hybrid bound (simultaneously in the depth and eigenvalue aspects) for the sup-norm; however, we do not attempt to do so here. The method of this paper can be combined with the Fourier/Whittaker expansion at various cusps in the adelic context (the necessary machinery for which is now available thanks to recent work of Assing [Reference AssingAss19] building on earlier work of the second author [Reference SahaSah16, Reference SahaSah17]) to give a depth-aspect sub-local bound in the case ![]() $D = M_2({\mathbb {Q}})$ (possibly with a different exponent than in Theorem A due to some differences in the counting argument). Finally, this paper provides a general strategy of how one should go about improving the local bound in the level aspect in cases where the local vectors are not sufficiently localized. Essentially, the message is that one needs to combine a counting argument with a ‘decay of matrix coefficients’ argument to successfully attack this problem for a wide array of local and global families.
$D = M_2({\mathbb {Q}})$ (possibly with a different exponent than in Theorem A due to some differences in the counting argument). Finally, this paper provides a general strategy of how one should go about improving the local bound in the level aspect in cases where the local vectors are not sufficiently localized. Essentially, the message is that one needs to combine a counting argument with a ‘decay of matrix coefficients’ argument to successfully attack this problem for a wide array of local and global families.
2. Preliminaries
2.1 Basic notation
The basic notation used in this paper is by and large the same as that in [Reference SahaSah20], but for convenience we recall it here.
2.1.1 Generalities
Let ![]() ${\mathbf {f}}$ denote the finite places of
${\mathbf {f}}$ denote the finite places of ![]() ${\mathbb {Q}}$ (which we identify with the set of primes) and
${\mathbb {Q}}$ (which we identify with the set of primes) and ![]() $\infty$ the archimedean place. We let
$\infty$ the archimedean place. We let ![]() ${\mathbb {A}}$ denote the ring of adeles over
${\mathbb {A}}$ denote the ring of adeles over ![]() ${\mathbb {Q}}$ and
${\mathbb {Q}}$ and ![]() ${\mathbb {A}}_{\mathbf {f}}$ the ring of finite adeles. Given an algebraic group
${\mathbb {A}}_{\mathbf {f}}$ the ring of finite adeles. Given an algebraic group ![]() $H$ defined over
$H$ defined over ![]() ${\mathbb {Q}}$, a place
${\mathbb {Q}}$, a place ![]() $v$ of
$v$ of ![]() ${\mathbb {Q}}$, a subset of places
${\mathbb {Q}}$, a subset of places ![]() $U$ of
$U$ of ![]() ${\mathbb {Q}}$, and a positive integer
${\mathbb {Q}}$, and a positive integer ![]() $M$, we denote
$M$, we denote ![]() $H_v:= H({\mathbb {Q}}_v)$,
$H_v:= H({\mathbb {Q}}_v)$, ![]() $H_U:=\prod _{v \in U} H_v$,
$H_U:=\prod _{v \in U} H_v$, ![]() $H_M :=\prod _{p|M} H_p$. Given an element
$H_M :=\prod _{p|M} H_p$. Given an element ![]() $g$ in
$g$ in ![]() $H({\mathbb {Q}})$ (respectively, in
$H({\mathbb {Q}})$ (respectively, in ![]() $H({\mathbb {A}})$), we will use
$H({\mathbb {A}})$), we will use ![]() $g_p$ to denote the image of
$g_p$ to denote the image of ![]() $g$ in
$g$ in ![]() $H_p$ (respectively, the
$H_p$ (respectively, the ![]() $p$-component of
$p$-component of ![]() $g$); more generally, for any set of places
$g$); more generally, for any set of places ![]() $U$, we let
$U$, we let ![]() $g_U$ denote the image of
$g_U$ denote the image of ![]() $g$ in
$g$ in ![]() $H_U$.
$H_U$.
Given two integers ![]() $a$ and
$a$ and ![]() $b$, we use
$b$, we use ![]() $a|b$ to denote that
$a|b$ to denote that ![]() $a$ divides
$a$ divides ![]() $b$, and we use
$b$, and we use ![]() $a|b^\infty$ to denote that
$a|b^\infty$ to denote that ![]() $a|b^n$ for some positive integer
$a|b^n$ for some positive integer ![]() $n$. For any real number
$n$. For any real number ![]() $\alpha$, we let
$\alpha$, we let ![]() $\lfloor \alpha \rfloor$ denote the greatest integer less than or equal to
$\lfloor \alpha \rfloor$ denote the greatest integer less than or equal to ![]() $\alpha$ and we let
$\alpha$ and we let ![]() $\lceil \alpha \rceil$ denote the smallest integer greater than or equal to
$\lceil \alpha \rceil$ denote the smallest integer greater than or equal to ![]() $\alpha$. For any integer
$\alpha$. For any integer ![]() $A=\prod _{p\in {\mathbf {f}}} p^{a_p}$, we write
$A=\prod _{p\in {\mathbf {f}}} p^{a_p}$, we write
In other words, ![]() $A_1$ is the smallest integer such that
$A_1$ is the smallest integer such that ![]() $A$ divides
$A$ divides ![]() $A_1^2$.
$A_1^2$.
All representations of (topological) groups are assumed to be continuous and over the field of complex numbers.
2.1.2 Quaternions, orders, and groups
Throughout this paper, we fix an indefinite quaternion division algebra ![]() $D$ over
$D$ over ![]() ${\mathbb {Q}}$. We fix once and for all a maximal order
${\mathbb {Q}}$. We fix once and for all a maximal order ![]() ${\mathcal {O}}^\textrm {max}$ of
${\mathcal {O}}^\textrm {max}$ of ![]() $D$. All constants in the bounds in this paper will be allowed to depend on
$D$. All constants in the bounds in this paper will be allowed to depend on ![]() $D$ without explicit mention. We let
$D$ without explicit mention. We let ![]() $d$ denote the reduced discriminant of
$d$ denote the reduced discriminant of ![]() $D$, i.e. the product of all primes such that
$D$, i.e. the product of all primes such that ![]() $D_p$ is a division algebra. We let
$D_p$ is a division algebra. We let ![]() $\textrm {nr}$ be the reduced norm on
$\textrm {nr}$ be the reduced norm on ![]() $D^\times$.
$D^\times$.
We denote ![]() $G=D^\times$ and
$G=D^\times$ and ![]() $G' =PD^\times = D^\times /Z$, where
$G' =PD^\times = D^\times /Z$, where ![]() $Z$ denotes the centre of
$Z$ denotes the centre of ![]() $D^\times$. For each prime
$D^\times$. For each prime ![]() $p$, let
$p$, let ![]() $K_p=({\mathcal {O}}^\textrm {max}_p)^\times$ and let
$K_p=({\mathcal {O}}^\textrm {max}_p)^\times$ and let ![]() $K_p'$ denote the image of
$K_p'$ denote the image of ![]() $K_p$ in
$K_p$ in ![]() $G'_p$. Given an order
$G'_p$. Given an order ![]() ${\mathcal {O}}$ of
${\mathcal {O}}$ of ![]() $D$, we define a compact open subgroup of
$D$, we define a compact open subgroup of ![]() $G({\mathbb {A}}_{\mathbf {f}})$ by
$G({\mathbb {A}}_{\mathbf {f}})$ by
For each place ![]() $v$ that is not among the primes dividing
$v$ that is not among the primes dividing ![]() $d$, fix once and for all an isomorphism
$d$, fix once and for all an isomorphism ![]() $\iota _v: D_v \xrightarrow {\cong } M(2,{\mathbb {Q}}_v)$. We assume that these isomorphisms are chosen such that for each finite prime
$\iota _v: D_v \xrightarrow {\cong } M(2,{\mathbb {Q}}_v)$. We assume that these isomorphisms are chosen such that for each finite prime ![]() $p\nmid d$, we have
$p\nmid d$, we have ![]() $\iota _p({\mathcal {O}}_p) = M(2,{\mathbb {Z}}_p)$. By abuse of notation, we also use
$\iota _p({\mathcal {O}}_p) = M(2,{\mathbb {Z}}_p)$. By abuse of notation, we also use ![]() $\iota _v$ to denote the composition map
$\iota _v$ to denote the composition map ![]() $D({\mathbb {Q}}) \rightarrow D_v \rightarrow M(2,{\mathbb {Q}}_v)$.
$D({\mathbb {Q}}) \rightarrow D_v \rightarrow M(2,{\mathbb {Q}}_v)$.
For any lattice ![]() ${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$ of
${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$ of ![]() $D$, we get a local lattice
$D$, we get a local lattice ![]() ${\mathcal {L}}_p$ of
${\mathcal {L}}_p$ of ![]() $D_p$ by localizing at each prime
$D_p$ by localizing at each prime ![]() $p$. These collections of lattices satisfy
$p$. These collections of lattices satisfy
Conversely, if we are given a collection of local lattices ![]() $\{{\mathcal {L}}_p\}_{p \in {\mathbf {f}}}$ such that
$\{{\mathcal {L}}_p\}_{p \in {\mathbf {f}}}$ such that ![]() ${\mathcal {L}}_p \subseteq {\mathcal {O}}^\textrm {max}_p$ for all
${\mathcal {L}}_p \subseteq {\mathcal {O}}^\textrm {max}_p$ for all ![]() $p$ and
$p$ and ![]() ${\mathcal {L}}_p = {\mathcal {O}}^\textrm {max}_p$ for all but finitely many
${\mathcal {L}}_p = {\mathcal {O}}^\textrm {max}_p$ for all but finitely many ![]() $p$, then there exists a unique lattice
$p$, then there exists a unique lattice ![]() ${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$ of
${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$ of ![]() $D$ defined via (5) and whose localizations at primes
$D$ defined via (5) and whose localizations at primes ![]() $p$ are precisely the
$p$ are precisely the ![]() ${\mathcal {L}}_p$. We will refer to
${\mathcal {L}}_p$. We will refer to ![]() ${\mathcal {L}}$ as the global lattice corresponding to the collection of local lattices
${\mathcal {L}}$ as the global lattice corresponding to the collection of local lattices ![]() $\{{\mathcal {L}}_p\}_{p \in {\mathbf {f}}}$. More generally, given a finite subset
$\{{\mathcal {L}}_p\}_{p \in {\mathbf {f}}}$. More generally, given a finite subset ![]() $S \subseteq {\mathbf {f}}$ and a collection of local lattices
$S \subseteq {\mathbf {f}}$ and a collection of local lattices ![]() $\{{\mathcal {L}}_p\}_{p \in S}$, we can construct the (unique) lattice whose localization at a prime
$\{{\mathcal {L}}_p\}_{p \in S}$, we can construct the (unique) lattice whose localization at a prime ![]() $p$ equals
$p$ equals ![]() ${\mathcal {L}}_p$ if
${\mathcal {L}}_p$ if ![]() $p\in S$ and equals
$p\in S$ and equals ![]() ${\mathcal {O}}_p^\textrm {max}$ if
${\mathcal {O}}_p^\textrm {max}$ if ![]() $p \notin S$; we will refer to this lattice as the global lattice corresponding to
$p \notin S$; we will refer to this lattice as the global lattice corresponding to ![]() $\{{\mathcal {L}}_p\}_{p \in S}$.
$\{{\mathcal {L}}_p\}_{p \in S}$.
Let ![]() ${\mathcal {L}}$ be a lattice in
${\mathcal {L}}$ be a lattice in ![]() $D$ such that
$D$ such that ![]() ${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$. We say that
${\mathcal {L}}\subseteq {\mathcal {O}}^\textrm {max}$. We say that ![]() ${\mathcal {L}}$ is tidy in
${\mathcal {L}}$ is tidy in ![]() ${\mathcal {O}}^\textrm {max}$ if
${\mathcal {O}}^\textrm {max}$ if ![]() ${\mathcal {L}}$ contains 1 and
${\mathcal {L}}$ contains 1 and ![]() $M_3^2$ divides
$M_3^2$ divides ![]() $N=[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}]$, where
$N=[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}]$, where ![]() $(M_1, M_2, M_3)$ is the unique triple of positive integers such that
$(M_1, M_2, M_3)$ is the unique triple of positive integers such that ![]() $M_1|M_2|M_3$ and
$M_1|M_2|M_3$ and ![]() ${\mathcal {O}}^\textrm {max} /{\mathcal {L}} \simeq ({\mathbb {Z}} / M_1{\mathbb {Z}}) \times ({\mathbb {Z}} / M_2{\mathbb {Z}}) \times ({\mathbb {Z}} / M_3{\mathbb {Z}}).$ Note that since
${\mathcal {O}}^\textrm {max} /{\mathcal {L}} \simeq ({\mathbb {Z}} / M_1{\mathbb {Z}}) \times ({\mathbb {Z}} / M_2{\mathbb {Z}}) \times ({\mathbb {Z}} / M_3{\mathbb {Z}}).$ Note that since ![]() $N=M_1M_2M_3$,
$N=M_1M_2M_3$, ![]() $M_3^2$ divides
$M_3^2$ divides ![]() $N$ if and only if
$N$ if and only if ![]() $N$ divides
$N$ divides ![]() $(M_1M_2)^2$ if and only if
$(M_1M_2)^2$ if and only if ![]() $M_3$ divides
$M_3$ divides ![]() $M_1M_2$. Let
$M_1M_2$. Let ![]() ${\mathcal {L}}_p$ be a lattice of
${\mathcal {L}}_p$ be a lattice of ![]() $D_p$ such that
$D_p$ such that ![]() ${\mathcal {L}}_p\subseteq {\mathcal {O}}_p^\textrm {max}$. We say that
${\mathcal {L}}_p\subseteq {\mathcal {O}}_p^\textrm {max}$. We say that ![]() ${\mathcal {L}}_p$ is tidy in
${\mathcal {L}}_p$ is tidy in ![]() ${\mathcal {O}}_p^\textrm {max}$ if
${\mathcal {O}}_p^\textrm {max}$ if ![]() $1 \in {\mathcal {L}}_p$ and
$1 \in {\mathcal {L}}_p$ and ![]() $m_3 \leqslant m_1+m_2$, where
$m_3 \leqslant m_1+m_2$, where ![]() $(m_1, m_2, m_3)$ is the unique triple of non-negative integers such that
$(m_1, m_2, m_3)$ is the unique triple of non-negative integers such that ![]() $m_1\leqslant m_2 \leqslant m_3$ and
$m_1\leqslant m_2 \leqslant m_3$ and ![]() ${\mathcal {O}}^\textrm {max}_p/{\mathcal {L}}_p \simeq ({\mathbb {Z}}_p / p^{m_1}{\mathbb {Z}}_p) \times ({\mathbb {Z}}_p / p^{m_2}{\mathbb {Z}}_p) \times ({\mathbb {Z}}_p / p^{m_3}{\mathbb {Z}}_p).$ It is clear that a global lattice
${\mathcal {O}}^\textrm {max}_p/{\mathcal {L}}_p \simeq ({\mathbb {Z}}_p / p^{m_1}{\mathbb {Z}}_p) \times ({\mathbb {Z}}_p / p^{m_2}{\mathbb {Z}}_p) \times ({\mathbb {Z}}_p / p^{m_3}{\mathbb {Z}}_p).$ It is clear that a global lattice ![]() ${\mathcal {L}}$ is tidy in
${\mathcal {L}}$ is tidy in ![]() ${\mathcal {O}}^\textrm {max}$ if and only if all the corresponding local lattices
${\mathcal {O}}^\textrm {max}$ if and only if all the corresponding local lattices ![]() ${\mathcal {L}}_p$ are tidy in
${\mathcal {L}}_p$ are tidy in ![]() ${\mathcal {O}}^\textrm {max}_p$.
${\mathcal {O}}^\textrm {max}_p$.
For each ![]() $g \in G({\mathbb {A}}_{\mathbf {f}})$ and a lattice
$g \in G({\mathbb {A}}_{\mathbf {f}})$ and a lattice ![]() ${\mathcal {L}}$ of
${\mathcal {L}}$ of ![]() $D$, we let
$D$, we let ![]() ${}^g{\mathcal {L}}$ denote the lattice whose localization at each prime
${}^g{\mathcal {L}}$ denote the lattice whose localization at each prime ![]() $p$ equals
$p$ equals ![]() $g_p {\mathcal {L}}_p g_p^{-1}$. Note that if
$g_p {\mathcal {L}}_p g_p^{-1}$. Note that if ![]() $g \in K_{{\mathcal {O}}^\textrm {max}}$ and
$g \in K_{{\mathcal {O}}^\textrm {max}}$ and ![]() ${\mathcal {L}}$ is tidy in
${\mathcal {L}}$ is tidy in ![]() ${\mathcal {O}}^\textrm {max}$, then
${\mathcal {O}}^\textrm {max}$, then ![]() ${}^g{\mathcal {L}}$ is also tidy in
${}^g{\mathcal {L}}$ is also tidy in ![]() ${\mathcal {O}}^\textrm {max}$.
${\mathcal {O}}^\textrm {max}$.
2.1.3 Haar measures
We fix the Haar measure on each group ![]() $G_p$ such that
$G_p$ such that ![]() $\operatorname {vol}(K_p)=1$. We fix a Haar measure on
$\operatorname {vol}(K_p)=1$. We fix a Haar measure on ![]() ${\mathbb {Q}}_p^\times$ such that
${\mathbb {Q}}_p^\times$ such that ![]() $\operatorname {vol}({\mathbb {Z}}_p^\times )=1$. This gives us resulting Haar measures on each group
$\operatorname {vol}({\mathbb {Z}}_p^\times )=1$. This gives us resulting Haar measures on each group ![]() $G'_p$ such that
$G'_p$ such that ![]() $\operatorname {vol}(K'_p)=1$. Fix any Haar measure on
$\operatorname {vol}(K'_p)=1$. Fix any Haar measure on ![]() $G_\infty$ and take the Haar measure on
$G_\infty$ and take the Haar measure on ![]() ${\mathbb {R}}^\times$ to be equal to
${\mathbb {R}}^\times$ to be equal to ![]() ${d}x/|x|$, where
${d}x/|x|$, where ![]() $dx$ is the Lebesgue measure. This gives us a Haar measure on
$dx$ is the Lebesgue measure. This gives us a Haar measure on ![]() $G'_\infty$. Take the measures on
$G'_\infty$. Take the measures on ![]() $G({\mathbb {A}})$ and
$G({\mathbb {A}})$ and ![]() $G'({\mathbb {A}})$ to be given by the product measure.
$G'({\mathbb {A}})$ to be given by the product measure.
For each continuous function ![]() $\phi$ on the space
$\phi$ on the space ![]() $G({\mathbb {A}})$, we let
$G({\mathbb {A}})$, we let ![]() $R(g)$ denote the right-regular action, given by
$R(g)$ denote the right-regular action, given by ![]() $(R(g)\phi )(h) = \phi (hg)$. If a continuous function
$(R(g)\phi )(h) = \phi (hg)$. If a continuous function ![]() $\phi$ on
$\phi$ on ![]() $G({\mathbb {A}})$ satisfies that
$G({\mathbb {A}})$ satisfies that ![]() $|\phi |$ is left
$|\phi |$ is left ![]() $Z({\mathbb {A}})G({\mathbb {Q}})$ invariant, define
$Z({\mathbb {A}})G({\mathbb {Q}})$ invariant, define
 \begin{equation} \|\phi\|_2 = \bigg(\int_{G'({\mathbb{Q}})\backslash G'({\mathbb{A}})} |\phi(g)|^2\,dg\bigg)^{1/2}. \end{equation}
\begin{equation} \|\phi\|_2 = \bigg(\int_{G'({\mathbb{Q}})\backslash G'({\mathbb{A}})} |\phi(g)|^2\,dg\bigg)^{1/2}. \end{equation}
Note above that ![]() $G'({\mathbb {Q}})\backslash G'({\mathbb {A}})$ is compact, so convergence of the integral is not an issue.
$G'({\mathbb {Q}})\backslash G'({\mathbb {A}})$ is compact, so convergence of the integral is not an issue.
2.1.4 Asymptotic notation
We use the notation ![]() $A \ll _{x,..,y} B$ to signify that there exists a quantity
$A \ll _{x,..,y} B$ to signify that there exists a quantity ![]() $C$ depending only on
$C$ depending only on ![]() $x,..,y$ (and possibly on any objects fixed throughout the paper) so that
$x,..,y$ (and possibly on any objects fixed throughout the paper) so that ![]() $|A| \leqslant C |B|$. We use
$|A| \leqslant C |B|$. We use ![]() $A \asymp _{x,..y} B$ to mean that
$A \asymp _{x,..y} B$ to mean that ![]() $A \ll _{x,..y} B$ and
$A \ll _{x,..y} B$ and ![]() $B \ll _{x,..y} A$. The symbol
$B \ll _{x,..y} A$. The symbol ![]() $\epsilon$ will denote a small positive quantity whose value may change from line to line; a statement such as
$\epsilon$ will denote a small positive quantity whose value may change from line to line; a statement such as ![]() $A \ll _{\epsilon , x,..} B$ should be read as ‘For all small
$A \ll _{\epsilon , x,..} B$ should be read as ‘For all small ![]() $\epsilon >0$, there is a quantity
$\epsilon >0$, there is a quantity ![]() $C$ that depends only on
$C$ that depends only on ![]() $\epsilon , x,..,$ and on any objects fixed throughout the paper such that
$\epsilon , x,..,$ and on any objects fixed throughout the paper such that ![]() $|A| \leqslant C |B|$.’ An assertion such as
$|A| \leqslant C |B|$.’ An assertion such as ![]() $A \ll _{x,..y} D^{O(1)} B$ means that there is a constant
$A \ll _{x,..y} D^{O(1)} B$ means that there is a constant ![]() $C$ such that
$C$ such that ![]() $|A| \ll _{x,..y} |D|^{C} |B|$.
$|A| \ll _{x,..y} |D|^{C} |B|$.
2.2 A counting result
Let ![]() $u(z_1, z_2)={|z_1 - z_2|^2 }/{4 \,\mathrm {Im}(z_1)\,\mathrm {Im}(z_2)}$, which is a function of the usual hyperbolic distance on
$u(z_1, z_2)={|z_1 - z_2|^2 }/{4 \,\mathrm {Im}(z_1)\,\mathrm {Im}(z_2)}$, which is a function of the usual hyperbolic distance on ![]() $\mathbb {H}$. For the convenience of the reader, we recall a counting result from [Reference SahaSah20] that will be used later.
$\mathbb {H}$. For the convenience of the reader, we recall a counting result from [Reference SahaSah20] that will be used later.
Proposition 2.1 For a compact subset ![]() ${\mathcal {J}}$ of
${\mathcal {J}}$ of ![]() $\mathbb {H}$ and a tidy lattice
$\mathbb {H}$ and a tidy lattice ![]() ${\mathcal {L}} \subseteq {\mathcal {O}}^\textrm {max}$ with
${\mathcal {L}} \subseteq {\mathcal {O}}^\textrm {max}$ with ![]() $[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}]=N$, the following bounds hold for all
$[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}]=N$, the following bounds hold for all ![]() $z \in {\mathcal {J}}$:
$z \in {\mathcal {J}}$:
 \begin{gather} \sum_{1\leqslant m \leqslant L } |\{\alpha \in {\mathcal{L}}: {\rm nr}(\alpha)=m, u(z, \iota_\infty(\alpha) z) \leqslant \delta\}| \ll_{\epsilon, \delta, {\mathcal{J}}} L^\epsilon N^{\epsilon} \biggl( L +\frac{L^2}{N} \biggr), \end{gather}
\begin{gather} \sum_{1\leqslant m \leqslant L } |\{\alpha \in {\mathcal{L}}: {\rm nr}(\alpha)=m, u(z, \iota_\infty(\alpha) z) \leqslant \delta\}| \ll_{\epsilon, \delta, {\mathcal{J}}} L^\epsilon N^{\epsilon} \biggl( L +\frac{L^2}{N} \biggr), \end{gather} \begin{gather} \sum_{1\leqslant m \leqslant L } |\{\alpha \in {\mathcal{L}}: {\rm nr}(\alpha)=m^2, u(z, \iota_\infty(\alpha) z) \leqslant \delta\}| \ll_{\epsilon, \delta,{\mathcal{J}}} L^\epsilon N^{\epsilon} \biggl(L +\frac{L^3}{N} \biggr). \end{gather}
\begin{gather} \sum_{1\leqslant m \leqslant L } |\{\alpha \in {\mathcal{L}}: {\rm nr}(\alpha)=m^2, u(z, \iota_\infty(\alpha) z) \leqslant \delta\}| \ll_{\epsilon, \delta,{\mathcal{J}}} L^\epsilon N^{\epsilon} \biggl(L +\frac{L^3}{N} \biggr). \end{gather}Proof. This is an immediate corollary of [Reference SahaSah20, Proposition 2.8 and Remark 2.11]. Note that Proposition 2.8 of [Reference SahaSah20] has the additional assumption ![]() $1 \leqslant L \leqslant N^{O(1)}$. However, as is clear from the proof of that proposition, the assumption was used there for the sole purpose of replacing any
$1 \leqslant L \leqslant N^{O(1)}$. However, as is clear from the proof of that proposition, the assumption was used there for the sole purpose of replacing any ![]() $L^\epsilon$ factors by
$L^\epsilon$ factors by ![]() $N^\epsilon$. Here, we have removed that assumption and instead included additional factors of
$N^\epsilon$. Here, we have removed that assumption and instead included additional factors of ![]() $L^\epsilon$ on the right-hand sides of each of (7) and (8).
$L^\epsilon$ on the right-hand sides of each of (7) and (8).
Remark 2.2 The above result is the main reason why we introduced the concept of ‘tidy’. For non-tidy lattices, the counting result gets more complicated, as demonstrated in Proposition 2.8 of [Reference SahaSah20].
3. Local families
For each prime ![]() $p \in {\mathbf {f}}$, we let
$p \in {\mathbf {f}}$, we let ![]() $\Pi (G_p)$ denote the set of isomorphism classes of representations
$\Pi (G_p)$ denote the set of isomorphism classes of representations ![]() $\pi$ of
$\pi$ of ![]() $G_p$ that are irreducible, admissible, unitary, and, if
$G_p$ that are irreducible, admissible, unitary, and, if ![]() $p\nmid d$, also infinite dimensional. Let
$p\nmid d$, also infinite dimensional. Let
Definition 3.1 A local family (over ![]() $G_p$) is a subset of
$G_p$) is a subset of ![]() ${\mathcal {A}}_p$.
${\mathcal {A}}_p$.
We will typically use ![]() ${\mathcal {F}}_p$ to denote a local family over
${\mathcal {F}}_p$ to denote a local family over ![]() $G_p$ and sometimes write the elements of
$G_p$ and sometimes write the elements of ![]() ${\mathcal {F}}_p$ as
${\mathcal {F}}_p$ as ![]() ${\mathcal {F}}_p = \{({\mathbb {C}} v_{i,p} , \pi _{i,p})_{i \in S_p}\}$, where
${\mathcal {F}}_p = \{({\mathbb {C}} v_{i,p} , \pi _{i,p})_{i \in S_p}\}$, where ![]() $S_p$ denotes an indexing set.
$S_p$ denotes an indexing set.
Definition 3.2 For each ![]() $p \in {\mathbf {f}}$, we let
$p \in {\mathbf {f}}$, we let ![]() ${\mathcal {F}}_p^{\textbf {ur}}$ denote the local family consisting of all the pairs
${\mathcal {F}}_p^{\textbf {ur}}$ denote the local family consisting of all the pairs ![]() $({\mathbb {C}} v, \pi )$ such that
$({\mathbb {C}} v, \pi )$ such that ![]() $\pi \in {\mathcal {A}}_p$ has the unique
$\pi \in {\mathcal {A}}_p$ has the unique ![]() $K_p$-fixed line
$K_p$-fixed line ![]() ${\mathbb {C}} v$.
${\mathbb {C}} v$.
For each ![]() $p \nmid d$,
$p \nmid d$, ![]() $\pi \in \Pi (G_p)$, let
$\pi \in \Pi (G_p)$, let ![]() $a(\pi ) \in {\mathbb {Z}}_{\geqslant 0}$ denote the exponent in the conductor of
$a(\pi ) \in {\mathbb {Z}}_{\geqslant 0}$ denote the exponent in the conductor of ![]() $\pi$. We write
$\pi$. We write ![]() $a_1(\pi ) = \lceil {a(\pi )}/{2}\rceil .$
$a_1(\pi ) = \lceil {a(\pi )}/{2}\rceil .$
Definition 3.3 A nice local family over ![]() $G_p$ is a subset
$G_p$ is a subset ![]() ${\mathcal {F}}_p$ of
${\mathcal {F}}_p$ of ![]() ${\mathcal {A}}_p$ with the following properties.
${\mathcal {A}}_p$ with the following properties.
(i) If
 $p|d$, then
$p|d$, then  ${\mathcal {F}}_p = {\mathcal {F}}_p^\textbf {ur}$.
${\mathcal {F}}_p = {\mathcal {F}}_p^\textbf {ur}$.(ii) If
 $p\nmid d$, then
$p\nmid d$, then
 \[ {\mathcal{F}}_p \cap \{( {\mathbb{C}} v, \pi): \pi \in \Pi(G_p), a(\pi)=0\} = {\mathcal{F}}_p^\textbf{ur}. \]
\[ {\mathcal{F}}_p \cap \{( {\mathbb{C}} v, \pi): \pi \in \Pi(G_p), a(\pi)=0\} = {\mathcal{F}}_p^\textbf{ur}. \]
Definition 3.4 A nice collection of local families (or, simply, a nice collection) is a tuple of the form ![]() ${\mathcal {F}} = ({\mathcal {F}}_p)_{p\in {\mathbf {f}}}$ such that for each prime
${\mathcal {F}} = ({\mathcal {F}}_p)_{p\in {\mathbf {f}}}$ such that for each prime ![]() $p \in {\mathbf {f}}$,
$p \in {\mathbf {f}}$, ![]() ${\mathcal {F}}_p$ is a nice local family over
${\mathcal {F}}_p$ is a nice local family over ![]() $G_p$.
$G_p$.
Remark 3.5 Note that a nice local family does not have any ‘old vectors’ originating from spherical (i.e. ![]() $K_p$-fixed) vectors. Furthermore, nice collections have no complications at the places dividing
$K_p$-fixed) vectors. Furthermore, nice collections have no complications at the places dividing ![]() $d$. We will restrict to nice families/collections for technical convenience and to get a cleaner statement of our main global theorem later on.
$d$. We will restrict to nice families/collections for technical convenience and to get a cleaner statement of our main global theorem later on.
The following definition quantifies the decay of a matrix coefficient along a filtration of compact subsets, needed for our main theorem.
Definition 3.6 Let ![]() $\eta _1$,
$\eta _1$, ![]() $\eta _2$,
$\eta _2$, ![]() $\delta$ be non-negative real numbers such that
$\delta$ be non-negative real numbers such that ![]() $\eta _1 \leqslant \eta _2$. Let
$\eta _1 \leqslant \eta _2$. Let ![]() ${\mathcal {F}}=({\mathcal {F}}_p)_{p\in {\mathbf {f}}}$ be a nice collection and, for each
${\mathcal {F}}=({\mathcal {F}}_p)_{p\in {\mathbf {f}}}$ be a nice collection and, for each ![]() $p \in {\mathbf {f}}$, write
$p \in {\mathbf {f}}$, write ![]() ${\mathcal {F}}_p = \{({\mathbb {C}} v_{i,p}, \pi _{i,p})_{i\in S_p}\}$, where
${\mathcal {F}}_p = \{({\mathbb {C}} v_{i,p}, \pi _{i,p})_{i\in S_p}\}$, where ![]() $S_p$ is any indexing set for
$S_p$ is any indexing set for ![]() ${\mathcal {F}}_p$. We say that
${\mathcal {F}}_p$. We say that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _2)$ if there exists
$(\eta _1, \delta ; \eta _2)$ if there exists ![]() $c\geqslant 0$ (
$c\geqslant 0$ (![]() $c$ depending only on
$c$ depending only on ![]() ${\mathcal {F}}, \eta _1, \eta _2$) and, furthermore, for each
${\mathcal {F}}, \eta _1, \eta _2$) and, furthermore, for each ![]() $p\nmid d$ and
$p\nmid d$ and ![]() $i \in S_p$ such that
$i \in S_p$ such that ![]() $a(\pi _{i,p})>0$, there exists an element
$a(\pi _{i,p})>0$, there exists an element ![]() $g_{i,p} \in G_p$, so that using the shorthand
$g_{i,p} \in G_p$, so that using the shorthand
 \[ v'_{i,p}:=\pi_{i,p}(g_{i,p})v_{i,p}, \quad \Phi'_{i,p}(g) = \frac{\langle \pi_{i,p}(g) v'_{i,p}, v'_{i,p}\rangle}{\langle v'_{i,p}, v'_{i,p} \rangle}, \]
\[ v'_{i,p}:=\pi_{i,p}(g_{i,p})v_{i,p}, \quad \Phi'_{i,p}(g) = \frac{\langle \pi_{i,p}(g) v'_{i,p}, v'_{i,p}\rangle}{\langle v'_{i,p}, v'_{i,p} \rangle}, \]
the conditions (1) and (2) below hold for each ![]() $p\in {\mathbf {f}}$,
$p\in {\mathbf {f}}$, ![]() $p\nmid d$,
$p\nmid d$, ![]() $i \in S_p$ for which
$i \in S_p$ for which ![]() $a(\pi _{i,p})>0$.
$a(\pi _{i,p})>0$.
(1) There exists a tidy order
 ${\mathcal {O}}_{i,p} \subseteq {\mathcal {O}}_p^\textrm {max}$ such that:
${\mathcal {O}}_{i,p} \subseteq {\mathcal {O}}_p^\textrm {max}$ such that:
(a)
 $[{\mathcal {O}}_p^\textrm {max}:{\mathcal {O}}_{i,p}] \ll p^{\eta _1 a_1(\pi _{i,p}) + c(\eta _2 - \eta _1)}$;
$[{\mathcal {O}}_p^\textrm {max}:{\mathcal {O}}_{i,p}] \ll p^{\eta _1 a_1(\pi _{i,p}) + c(\eta _2 - \eta _1)}$;(b) the
 $\pi _{i,p}$-action of
$\pi _{i,p}$-action of  ${\mathcal {O}}_{i,p}^\times$ on
${\mathcal {O}}_{i,p}^\times$ on  $v_{i,p}'$ generates an irreducible representation of dimension
$v_{i,p}'$ generates an irreducible representation of dimension  $\ll p^{\delta a_1(\pi _{i,p})}$.
$\ll p^{\delta a_1(\pi _{i,p})}$.
(2) For each
 $\eta$ satisfying
$\eta$ satisfying  $\eta _1 < \eta \leqslant \eta _2$, there exists a tidy lattice
$\eta _1 < \eta \leqslant \eta _2$, there exists a tidy lattice  ${\mathcal {L}}^\eta _{i,p} \subseteq {\mathcal {O}}_{i,p}$ such that:
${\mathcal {L}}^\eta _{i,p} \subseteq {\mathcal {O}}_{i,p}$ such that:
(a)
 ${\mathcal {L}}^{\eta '}_{i,p} \subseteq {\mathcal {L}}^{\eta }_{i,p}$ for all
${\mathcal {L}}^{\eta '}_{i,p} \subseteq {\mathcal {L}}^{\eta }_{i,p}$ for all  $\eta _1<\eta \leqslant \eta ' \leqslant \eta _2$;
$\eta _1<\eta \leqslant \eta ' \leqslant \eta _2$;(b)
 $p^{\eta a_1(\pi _{i,p})-c} \ll [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _{i,p}] \ll p^{\eta a_1(\pi _{i,p})+c}$;
$p^{\eta a_1(\pi _{i,p})-c} \ll [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _{i,p}] \ll p^{\eta a_1(\pi _{i,p})+c}$;(c) if
 $g \in {\mathcal {O}}_{i,p}^\times$,
$g \in {\mathcal {O}}_{i,p}^\times$,  $g \notin {\mathcal {L}}^\eta _{i,p}$, we have
$g \notin {\mathcal {L}}^\eta _{i,p}$, we have  $|\Phi '_{i,p}(g)| \ll p^{c+ (\eta -\eta _2) a_1(\pi _{i,p})}.$
$|\Phi '_{i,p}(g)| \ll p^{c+ (\eta -\eta _2) a_1(\pi _{i,p})}.$
Remark 3.7 Suppose we have a collection ![]() ${\mathcal {F}}$ which is controlled by
${\mathcal {F}}$ which is controlled by ![]() $(\eta _1, \delta ; \eta _2)$. Then it is trivially true that
$(\eta _1, \delta ; \eta _2)$. Then it is trivially true that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _2')$ for any
$(\eta _1, \delta ; \eta _2')$ for any ![]() $\eta _1 \leqslant \eta _2' \leqslant \eta _2$. Therefore, whenever we assert that
$\eta _1 \leqslant \eta _2' \leqslant \eta _2$. Therefore, whenever we assert that ![]() ${\mathcal {F}}$ is controlled by some
${\mathcal {F}}$ is controlled by some ![]() $(\eta _1, \delta ; \eta _2)$, we will try and ensure that we choose
$(\eta _1, \delta ; \eta _2)$, we will try and ensure that we choose ![]() $\eta _2$ as large as possible (for those particular values of
$\eta _2$ as large as possible (for those particular values of ![]() $\eta _1$ and
$\eta _1$ and ![]() $\delta$).
$\delta$).
Remark 3.8 Suppose that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _2)$. Let us explore the possible range of values that
$(\eta _1, \delta ; \eta _2)$. Let us explore the possible range of values that ![]() $\eta _1, \eta _2, \delta$ can take. We assume for the purpose of this remark that for each prime
$\eta _1, \eta _2, \delta$ can take. We assume for the purpose of this remark that for each prime ![]() $p$ either
$p$ either ![]() ${\mathcal {F}}_p = {\mathcal {F}}_p^\textbf {ur}$ or the set
${\mathcal {F}}_p = {\mathcal {F}}_p^\textbf {ur}$ or the set ![]() $\{a(\pi _{i,p}): i \in S_p\}$ is unbounded.
$\{a(\pi _{i,p}): i \in S_p\}$ is unbounded.
We first focus on the implications of condition (1). Let ![]() $i\in S_p$ with
$i\in S_p$ with ![]() $a(\pi _{i,p})>0$. Then condition (1) implies that
$a(\pi _{i,p})>0$. Then condition (1) implies that
Now it can be shown (by formal degree considerations) that for ![]() $\pi _{i,p}$ discrete series, the left-hand side above is
$\pi _{i,p}$ discrete series, the left-hand side above is ![]() $\ll p^{-a_1(\pi _{i,p})}$. In fact, an explicit computation (performed in [Reference SahaSah17]) shows that the same holds for principal series. Therefore (by letting
$\ll p^{-a_1(\pi _{i,p})}$. In fact, an explicit computation (performed in [Reference SahaSah17]) shows that the same holds for principal series. Therefore (by letting ![]() $i \rightarrow \infty$), we obtain the inequality
$i \rightarrow \infty$), we obtain the inequality
This inequality is sharp in the sense that there exist several collections ![]() ${\mathcal {F}}$ that satisfy condition (1) for some
${\mathcal {F}}$ that satisfy condition (1) for some ![]() $\eta _1$,
$\eta _1$, ![]() $\delta$ with
$\delta$ with ![]() $\eta _1 + \delta = 1$. Indeed, for many natural collections (including those that correspond locally to newvectors of trivial character, minimal vectors, and
$\eta _1 + \delta = 1$. Indeed, for many natural collections (including those that correspond locally to newvectors of trivial character, minimal vectors, and ![]() $p$-adic microlocal lifts) one can choose the order
$p$-adic microlocal lifts) one can choose the order ![]() ${\mathcal {O}}_{i,p} = {\mathcal {O}}^\textrm {max}_p$ to ensure that the condition (1) of Definition 3.6 holds with
${\mathcal {O}}_{i,p} = {\mathcal {O}}^\textrm {max}_p$ to ensure that the condition (1) of Definition 3.6 holds with ![]() $\eta _1=0$,
$\eta _1=0$, ![]() $\delta = 1$; see Proposition 2.13 of [Reference SahaSah17], § 1.4 and Remark 3.2 of [Reference SahaSah20], and Corollary A.3 of [Reference Hu and NelsonHN18].
$\delta = 1$; see Proposition 2.13 of [Reference SahaSah17], § 1.4 and Remark 3.2 of [Reference SahaSah20], and Corollary A.3 of [Reference Hu and NelsonHN18].
Next we explore what is the possible range of values that ![]() $\eta _2$ can take given
$\eta _2$ can take given ![]() $\eta _1$ and
$\eta _1$ and ![]() $\delta$. Combining (9) with condition (2) of Definition 3.6 and the triangle inequality, a simple computation leads to
$\delta$. Combining (9) with condition (2) of Definition 3.6 and the triangle inequality, a simple computation leads to
On the other hand, suppose we have a collection ![]() ${\mathcal {F}}$ satisfying condition (1) of Definition 3.6 for some
${\mathcal {F}}$ satisfying condition (1) of Definition 3.6 for some ![]() $\eta _1$,
$\eta _1$, ![]() $\delta$. Then it is trivially true that
$\delta$. Then it is trivially true that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _1)$.
$(\eta _1, \delta ; \eta _1)$.
So, to summarize, if a collection ![]() ${\mathcal {F}}$ satisfies condition (1) of Definition 3.6 for some
${\mathcal {F}}$ satisfies condition (1) of Definition 3.6 for some ![]() $\eta _1$,
$\eta _1$, ![]() $\delta$, then (10) holds, and if we then want to find some
$\delta$, then (10) holds, and if we then want to find some ![]() $\eta _2$ such that
$\eta _2$ such that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _2)$, then any such
$(\eta _1, \delta ; \eta _2)$, then any such ![]() $\eta _2$ must lie in the range
$\eta _2$ must lie in the range ![]() $[\eta _1, \eta _1 + \delta ]$. In this range,
$[\eta _1, \eta _1 + \delta ]$. In this range, ![]() $\eta _2=\eta _1$ always works.
$\eta _2=\eta _1$ always works.
Remark 3.9 In relation to the last remark, the main result of [Reference SahaSah20] tells us that whenever a collection satisfies condition (1) of Definition 3.6 with ![]() $\eta _1=\eta _2$ and
$\eta _1=\eta _2$ and ![]() ${\eta _1}/3 + {\delta }/2 <\frac {1}{2}$, then we can break the local bound for the sup-norms of the corresponding global automorphic forms. Unfortunately it is not always true that naturally occurring collections have this property.
${\eta _1}/3 + {\delta }/2 <\frac {1}{2}$, then we can break the local bound for the sup-norms of the corresponding global automorphic forms. Unfortunately it is not always true that naturally occurring collections have this property.
The crucial new ingredient in this paper is represented by condition ![]() $(2)$, which posits a linear decay result for the matrix coefficient associated to a suitable translate of
$(2)$, which posits a linear decay result for the matrix coefficient associated to a suitable translate of ![]() $v_{i,p}$. Whenever we can prove a quantitative decay of local matrix coefficients so that
$v_{i,p}$. Whenever we can prove a quantitative decay of local matrix coefficients so that ![]() ${\mathcal {F}}$ is controlled by
${\mathcal {F}}$ is controlled by ![]() $(\eta _1, \delta ; \eta _2)$ for some
$(\eta _1, \delta ; \eta _2)$ for some ![]() $\eta _2>\eta _1$, it will allow us (in our main global theorem, Theorem 4.6 below) to improve upon the sup-norm estimate obtained from condition (1) alone.
$\eta _2>\eta _1$, it will allow us (in our main global theorem, Theorem 4.6 below) to improve upon the sup-norm estimate obtained from condition (1) alone.
Remark 3.10 The assumption that the relevant lattices/orders in Definition 3.6 are tidy is in order to get a cleaner statement of Theorem 4.6 later on. However, this is not essential for our method and one could in principle omit from Definition 3.6 the condition that the lattices are tidy. However, in that case, Proposition 2.1 would need to be modified and Theorem 4.6 below would get more complicated.
Remark 3.11 One could refine Definition 3.6 by including the constant ![]() $c$ among the ‘controlling’ parameters, or by replacing
$c$ among the ‘controlling’ parameters, or by replacing ![]() $c$ with a function of
$c$ with a function of ![]() $i$ and
$i$ and ![]() $p$. Any such hybrid definition can be used to make a refinement of Theorem 4.6 below without much additional work. We avoid doing this in this paper in the interest of simplicity and because our main focus is in the depth aspect.
$p$. Any such hybrid definition can be used to make a refinement of Theorem 4.6 below without much additional work. We avoid doing this in this paper in the interest of simplicity and because our main focus is in the depth aspect.
Example 3.12 For each ![]() $p\nmid 2d$, define the local family
$p\nmid 2d$, define the local family ![]() ${\mathcal {F}}_p^{\min , *}$ to be the union of
${\mathcal {F}}_p^{\min , *}$ to be the union of ![]() ${\mathcal {F}}_p^\textbf {ur}$ and all pairs
${\mathcal {F}}_p^\textbf {ur}$ and all pairs ![]() $({\mathbb {C}} v, \pi )$ such that
$({\mathbb {C}} v, \pi )$ such that ![]() $\pi$ is a twist-minimal supercuspidal representation of
$\pi$ is a twist-minimal supercuspidal representation of ![]() $G_p$ satisfying
$G_p$ satisfying ![]() $a(\pi ) \not \equiv 2 \pmod {4}$ and
$a(\pi ) \not \equiv 2 \pmod {4}$ and ![]() $v$ is a minimal vector in
$v$ is a minimal vector in ![]() $\pi$ in the sense of [Reference Hu and NelsonHN18]. For
$\pi$ in the sense of [Reference Hu and NelsonHN18]. For ![]() $p|2d$, define
$p|2d$, define ![]() ${\mathcal {F}}_p^{\min , *} = {\mathcal {F}}_p^\textbf {ur}$. Let
${\mathcal {F}}_p^{\min , *} = {\mathcal {F}}_p^\textbf {ur}$. Let ![]() ${\mathcal {F}}^{\min , *}$ be the corresponding nice collection. Then, by the results of [Reference Hu and NelsonHN18],
${\mathcal {F}}^{\min , *}$ be the corresponding nice collection. Then, by the results of [Reference Hu and NelsonHN18], ![]() ${\mathcal {F}}^{\min , *}$ is controlled by
${\mathcal {F}}^{\min , *}$ is controlled by ![]() $(1,0;1)$. Furthermore, it follows from Remark 3.2 of [Reference SahaSah20] that
$(1,0;1)$. Furthermore, it follows from Remark 3.2 of [Reference SahaSah20] that ![]() ${\mathcal {F}}^{\min , *}$ is controlled by
${\mathcal {F}}^{\min , *}$ is controlled by ![]() $(\gamma , 1-\gamma ;1)$ for all
$(\gamma , 1-\gamma ;1)$ for all ![]() $0\leqslant \gamma \leqslant 1$. So, this is an example where equality is attained in both (10) and (11).
$0\leqslant \gamma \leqslant 1$. So, this is an example where equality is attained in both (10) and (11).
Definition 3.13 Let ![]() $p \nmid d$ be a prime. Define the nice local family
$p \nmid d$ be a prime. Define the nice local family ![]() ${\mathcal {F}}_p^{\textrm {new}, *}$ to consist of all pairs
${\mathcal {F}}_p^{\textrm {new}, *}$ to consist of all pairs ![]() $({\mathbb {C}} v, \pi )$ with
$({\mathbb {C}} v, \pi )$ with ![]() $\pi$ varying over the representations in
$\pi$ varying over the representations in ![]() $\Pi (G_p)$ with unramified central character, and
$\Pi (G_p)$ with unramified central character, and ![]() ${\mathbb {C}} v$ equal to the (unique) line generated by the local newvector.
${\mathbb {C}} v$ equal to the (unique) line generated by the local newvector.
The following result will follow from our work in § 5 of this paper.
Proposition 3.14 Let ![]() $\mathcal {G} = \{{\mathcal {G}}_p\}$ be the nice collection given by:
$\mathcal {G} = \{{\mathcal {G}}_p\}$ be the nice collection given by:
(i)
 ${\mathcal {G}}_p = {\mathcal {F}}_p^{{{\rm new}}, *}$ if
${\mathcal {G}}_p = {\mathcal {F}}_p^{{{\rm new}}, *}$ if  $p\nmid 2d$;
$p\nmid 2d$;(ii)
 ${\mathcal {G}}_p = {\mathcal {F}}_p^\textbf {ur}$ if
${\mathcal {G}}_p = {\mathcal {F}}_p^\textbf {ur}$ if  $p|2d$.
$p|2d$.
Then ![]() ${\mathcal {G}}$ is controlled by
${\mathcal {G}}$ is controlled by ![]() $(0,1; \frac 12)$.
$(0,1; \frac 12)$.
Remark 3.15 Roughly speaking, Proposition 3.14 asserts (among other things) that for each fixed odd prime ![]() $p$ and each local representation
$p$ and each local representation ![]() $\pi _p$ of
$\pi _p$ of ![]() $\textrm {GL}_2({\mathbb {Q}}_p)$ with
$\textrm {GL}_2({\mathbb {Q}}_p)$ with ![]() $a_1(\pi _p)=n_1$, there is a certain translate
$a_1(\pi _p)=n_1$, there is a certain translate ![]() $v'$ of the newform whose associated matrix coefficient
$v'$ of the newform whose associated matrix coefficient ![]() $\Phi '(g)$ is bounded by
$\Phi '(g)$ is bounded by ![]() $p^{-n_1/2} \ [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p]$ at matrices
$p^{-n_1/2} \ [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p]$ at matrices ![]() $g \notin {\mathcal {L}}^\eta _p$, where
$g \notin {\mathcal {L}}^\eta _p$, where ![]() $\{{\mathcal {L}}_p^{\eta }\}_{0 \leqslant \eta \leqslant \frac 12}$ is a suitable filtration of lattices in
$\{{\mathcal {L}}_p^{\eta }\}_{0 \leqslant \eta \leqslant \frac 12}$ is a suitable filtration of lattices in ![]() ${\mathcal {O}}_p^\textrm {max}$ such that
${\mathcal {O}}_p^\textrm {max}$ such that ![]() $[{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p] \asymp p^{\eta n_1 + O(1)}$.
$[{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p] \asymp p^{\eta n_1 + O(1)}$.
However, what we will end up proving in § 5 is the stronger statement that the matrix coefficient ![]() $\Phi '(g)$ is bounded by
$\Phi '(g)$ is bounded by ![]() $p^{-n_1/2} \ [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p]^{1/4}$ at such matrices.
$p^{-n_1/2} \ [{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p]^{1/4}$ at such matrices.
Unfortunately, this stronger bound does not help in improving the exponent ![]() $5/24$ in Theorem A. This is essentially because both the above bounds coincide when
$5/24$ in Theorem A. This is essentially because both the above bounds coincide when ![]() $[{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p] \asymp 1$.
$[{\mathcal {O}}_p^\textrm {max}:{\mathcal {L}}^\eta _p] \asymp 1$.
Remark 3.16 Let ![]() $k_0$ be some fixed non-negative integer. For each prime
$k_0$ be some fixed non-negative integer. For each prime ![]() $p$ not dividing
$p$ not dividing ![]() $2d$, consider the subset of
$2d$, consider the subset of ![]() ${\mathcal {F}}_p^{\textrm {new}, *}$ consisting of the pairs
${\mathcal {F}}_p^{\textrm {new}, *}$ consisting of the pairs ![]() $({\mathbb {C}} v_i, \pi _i) \in {\mathcal {F}}_p^{{\rm new}, \ast}$, where
$({\mathbb {C}} v_i, \pi _i) \in {\mathcal {F}}_p^{{\rm new}, \ast}$, where ![]() $a(\pi _i) \leqslant k_0$. Then, letting
$a(\pi _i) \leqslant k_0$. Then, letting ![]() $g_{i,p} = \iota _p^{-1}\big (\begin {smallmatrix}{p^{a_1(\pi _i)}} & {} \\ {} & {1}\end {smallmatrix}\big )$ and
$g_{i,p} = \iota _p^{-1}\big (\begin {smallmatrix}{p^{a_1(\pi _i)}} & {} \\ {} & {1}\end {smallmatrix}\big )$ and ![]() ${\mathcal {L}}^\eta _{i,p} = {\mathcal {O}}^\textrm {max}_{i,p}$, we see that the conditions in Definition 3.6 hold (trivially) for
${\mathcal {L}}^\eta _{i,p} = {\mathcal {O}}^\textrm {max}_{i,p}$, we see that the conditions in Definition 3.6 hold (trivially) for ![]() $\eta _1 =0$,
$\eta _1 =0$, ![]() $\delta =1$,
$\delta =1$, ![]() $\eta _2 = \frac 12$ with the constant
$\eta _2 = \frac 12$ with the constant ![]() $c$ equal to
$c$ equal to ![]() ${k_0}/2$. So, in order to prove Proposition 3.14, it suffices to restrict our attention only to representations
${k_0}/2$. So, in order to prove Proposition 3.14, it suffices to restrict our attention only to representations ![]() $\pi _i$ with
$\pi _i$ with ![]() $a(\pi _i)>k_0$. We will use this with
$a(\pi _i)>k_0$. We will use this with ![]() $k_0 = 2$ in § 5 when we prove the above proposition.
$k_0 = 2$ in § 5 when we prove the above proposition.
Furthermore, for the proof of Proposition 3.14, it suffices to restrict ourselves only to the pairs ![]() $({\mathbb {C}} v, \pi ) \in {\mathcal {F}}_p^{{\rm new}, \ast}$ where
$({\mathbb {C}} v, \pi ) \in {\mathcal {F}}_p^{{\rm new}, \ast}$ where ![]() $\pi _i$ has trivial central character. This is because any unitary representation of
$\pi _i$ has trivial central character. This is because any unitary representation of ![]() $\textrm {GL}_2({\mathbb {Q}}_p)$ with unramified central character can be twisted by
$\textrm {GL}_2({\mathbb {Q}}_p)$ with unramified central character can be twisted by ![]() $| \det (g) |_p^s$ for some suitable
$| \det (g) |_p^s$ for some suitable ![]() $s \in i{\mathbb {R}}$ to make it have trivial central character; the twisting action in this case takes newforms to newforms, and the matrix coefficients, etc., remain the same.
$s \in i{\mathbb {R}}$ to make it have trivial central character; the twisting action in this case takes newforms to newforms, and the matrix coefficients, etc., remain the same.
Remark 3.17 We suspect that Proposition 3.14 continues to hold for the larger collection where we allow (a) ![]() $p=2$, and (b) replace the condition of unramified central character with more general central characters. However, for simplicity, we restrict ourselves to this case.
$p=2$, and (b) replace the condition of unramified central character with more general central characters. However, for simplicity, we restrict ourselves to this case.
4. The main global result
Throughout this section, we will use the notation defined in §§ 2.1 and 3.
4.1 Global families
We let ![]() $\Pi (G)$ denote the set of irreducible, unitary, cuspidal automorphic representations of
$\Pi (G)$ denote the set of irreducible, unitary, cuspidal automorphic representations of ![]() $G({\mathbb {A}})$. For any
$G({\mathbb {A}})$. For any ![]() $\pi = \otimes _v \pi _v$ in
$\pi = \otimes _v \pi _v$ in ![]() $\Pi (G)$, we let
$\Pi (G)$, we let ![]() $C(\pi )=\prod _{p\nmid d} p^{a(\pi _p)}$ denote the conductorFootnote 10 of
$C(\pi )=\prod _{p\nmid d} p^{a(\pi _p)}$ denote the conductorFootnote 10 of ![]() $\otimes _{p\nmid d}\pi _p$, and we identify
$\otimes _{p\nmid d}\pi _p$, and we identify ![]() $V_\pi$ with a (unique) subspace of functions on
$V_\pi$ with a (unique) subspace of functions on ![]() $G({\mathbb {A}})$ so that
$G({\mathbb {A}})$ so that ![]() $\pi (g)$ coincides with the right-regular representation
$\pi (g)$ coincides with the right-regular representation ![]() $R(g)$ on that subspace. We define the integer
$R(g)$ on that subspace. We define the integer ![]() $C_1(\pi )$ as in (4); i.e.
$C_1(\pi )$ as in (4); i.e. ![]() $C_1(\pi )$ is the smallest integer such that
$C_1(\pi )$ is the smallest integer such that ![]() $C(\pi )$ divides
$C(\pi )$ divides ![]() $C_1(\pi )^2$. For any
$C_1(\pi )^2$. For any ![]() $\pi \in \Pi (G)$, define
$\pi \in \Pi (G)$, define
We denote
If ![]() $\phi$ is a function such that
$\phi$ is a function such that ![]() $({\mathbb {C}} \phi , \pi ) \in {\mathcal {A}}(G)$, then
$({\mathbb {C}} \phi , \pi ) \in {\mathcal {A}}(G)$, then ![]() $|\phi |$ is left
$|\phi |$ is left ![]() $Z({\mathbb {A}})G({\mathbb {Q}})$ invariant and hence we define
$Z({\mathbb {A}})G({\mathbb {Q}})$ invariant and hence we define ![]() $\|\phi \|_2$ as in (6). For any such
$\|\phi \|_2$ as in (6). For any such ![]() $\phi$, we say that
$\phi$, we say that ![]() $\phi$ is factorizable if
$\phi$ is factorizable if ![]() $\phi$ corresponds to a pure tensor under the isomorphismFootnote 11
$\phi$ corresponds to a pure tensor under the isomorphismFootnote 11 ![]() $\pi \simeq \otimes _{v} \pi _v$, in which case we write
$\pi \simeq \otimes _{v} \pi _v$, in which case we write ![]() $\phi = \otimes _v \phi _v$ with
$\phi = \otimes _v \phi _v$ with ![]() $\phi _v$ a vector in
$\phi _v$ a vector in ![]() $\pi _v$.
$\pi _v$.
Definition 4.1 For ![]() $({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G)$ and
$({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G)$ and ![]() $T>0$, we say that the archimedean parameters of
$T>0$, we say that the archimedean parameters of ![]() $({\mathbb {C}}\phi , \pi )$ are bounded by
$({\mathbb {C}}\phi , \pi )$ are bounded by ![]() $T$ if the following two conditions hold: (a) the analytic conductor
$T$ if the following two conditions hold: (a) the analytic conductor ![]() ${\mathfrak q}_\infty (\pi _\infty )$ (see [Reference Iwaniec and KowalskiIK04, p. 95] for the definition) of
${\mathfrak q}_\infty (\pi _\infty )$ (see [Reference Iwaniec and KowalskiIK04, p. 95] for the definition) of ![]() $\pi _\infty$ satisfies
$\pi _\infty$ satisfies ![]() ${\mathfrak q}_\infty (\pi _\infty ) \leqslant T$, and (b) the weight-vector decomposition of
${\mathfrak q}_\infty (\pi _\infty ) \leqslant T$, and (b) the weight-vector decomposition of ![]() $\phi$ under the action of
$\phi$ under the action of ![]() $\iota _\infty ^{-1}(\textrm {SO}(2))$ involves only weights
$\iota _\infty ^{-1}(\textrm {SO}(2))$ involves only weights ![]() $k$ such that
$k$ such that ![]() $|k|\leqslant T$.
$|k|\leqslant T$.
Remark 4.2 Let ![]() $\phi$ be a cuspidal automorphic form on
$\phi$ be a cuspidal automorphic form on ![]() $G({\mathbb {A}})$ that generates some representation
$G({\mathbb {A}})$ that generates some representation ![]() $\pi \in \Pi (G)$. Then it is easy to see that
$\pi \in \Pi (G)$. Then it is easy to see that ![]() $({\mathbb {C}}\phi , \pi )$ has its archimedean parameters bounded by some
$({\mathbb {C}}\phi , \pi )$ has its archimedean parameters bounded by some ![]() $T$ (since the usual definition of an automorphic form implies that
$T$ (since the usual definition of an automorphic form implies that ![]() $\phi$ is
$\phi$ is ![]() $K_\infty$-finite).
$K_\infty$-finite).
Definition 4.3 Given a nice collection ![]() ${\mathcal {F}}=({\mathcal {F}}_p)_{p \in {\mathbf {f}}}$ of local families, we define the corresponding global family of automorphic forms
${\mathcal {F}}=({\mathcal {F}}_p)_{p \in {\mathbf {f}}}$ of local families, we define the corresponding global family of automorphic forms ![]() ${\mathcal {A}}(G; {\mathcal {F}})$ as follows:
${\mathcal {A}}(G; {\mathcal {F}})$ as follows:
Definition 4.4 For each ![]() $T>0$, we let
$T>0$, we let ![]() ${\mathcal {A}}(G; {\mathcal {F}}, T) \subset {\mathcal {A}}(G; {\mathcal {F}})$ consist of all the
${\mathcal {A}}(G; {\mathcal {F}}, T) \subset {\mathcal {A}}(G; {\mathcal {F}})$ consist of all the ![]() $({\mathbb {C}}\phi , \pi )$ in
$({\mathbb {C}}\phi , \pi )$ in ![]() ${\mathcal {A}}(G; {\mathcal {F}})$ whose archimedean parameters are bounded by
${\mathcal {A}}(G; {\mathcal {F}})$ whose archimedean parameters are bounded by ![]() $T$.
$T$.
Remark 4.5 Suppose that ![]() ${\mathcal {F}}$ is a nice collection and
${\mathcal {F}}$ is a nice collection and ![]() $({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}},T)$. Then our definition of a nice collection implies that
$({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}},T)$. Then our definition of a nice collection implies that
4.2 Statement of the main theorem
We can now state the master theorem of this paper.
Theorem 4.6 Let ![]() $\eta _1$,
$\eta _1$, ![]() $\eta _2$,
$\eta _2$, ![]() $\delta$ be non-negative real numbers such that
$\delta$ be non-negative real numbers such that ![]() $\eta _1 \leqslant \eta _2$. Let
$\eta _1 \leqslant \eta _2$. Let ![]() ${\mathcal {F}}=({\mathcal {F}}_p)_{p \in {\mathbf {f}}}$ be a nice collection that is controlled by
${\mathcal {F}}=({\mathcal {F}}_p)_{p \in {\mathbf {f}}}$ be a nice collection that is controlled by ![]() $(\eta _1, \delta ; \eta _2)$. Then there is a non-negative constant
$(\eta _1, \delta ; \eta _2)$. Then there is a non-negative constant ![]() $x$ depending only on
$x$ depending only on ![]() ${\mathcal {F}}$,
${\mathcal {F}}$, ![]() $\eta _1$,
$\eta _1$, ![]() $\eta _2$ (we can take
$\eta _2$ (we can take ![]() $x=0$ if
$x=0$ if ![]() $\eta _1 = \eta _2$) such that for all
$\eta _1 = \eta _2$) such that for all ![]() $({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}}, T)$, we have
$({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}}, T)$, we have
The above theorem can be viewed as a generalization of Theorem 1 of [Reference SahaSah20], which dealt with the special caseFootnote 12 ![]() $\eta _1 = \eta _2$; in this special case, condition (2) of Definition 3.6 is vacuous and does not play any part.
$\eta _1 = \eta _2$; in this special case, condition (2) of Definition 3.6 is vacuous and does not play any part.
Remark 4.7 In previous sup-norm papers such as [Reference Hu, Nelson and SahaHNS19, Reference SahaSah16], we often restricted to automorphic forms which corresponded classically to Hecke eigenforms that are either Maass cusp forms of weight ![]() $0$ or holomorphic cusp forms of weight
$0$ or holomorphic cusp forms of weight ![]() $k$. Definition 4.1 above (see also Remark 4.2) allows us to state Theorem 4.6 for much more general automorphic forms.
$k$. Definition 4.1 above (see also Remark 4.2) allows us to state Theorem 4.6 for much more general automorphic forms.
Remark 4.8 As mentioned earlier, for many nice collections, condition (1) of Definition 3.6 holds with ![]() $\eta _1=0$,
$\eta _1=0$, ![]() $\delta = 1$. This gives us the ‘local bound’
$\delta = 1$. This gives us the ‘local bound’
for any ![]() $\phi$ belonging to the corresponding global family of automorphic forms. Theorem 4.6 gives us a pathway to go beyond (12) in this case whenever we can prove the existence of some
$\phi$ belonging to the corresponding global family of automorphic forms. Theorem 4.6 gives us a pathway to go beyond (12) in this case whenever we can prove the existence of some ![]() $\eta _2 > 0$ for which condition (2) of Definition 3.6 holds.
$\eta _2 > 0$ for which condition (2) of Definition 3.6 holds.
That this can indeed be done (with ![]() $\eta _2 = \frac 12$) for the collection corresponding to global newforms of odd conductor and trivial character is precisely the content of Proposition 3.14. This leads to the following corollary.
$\eta _2 = \frac 12$) for the collection corresponding to global newforms of odd conductor and trivial character is precisely the content of Proposition 3.14. This leads to the following corollary.
Corollary 4.9 Let ![]() $\mathcal {G}$ be as in Proposition 3.14. Let
$\mathcal {G}$ be as in Proposition 3.14. Let ![]() $C$ be a positive integer such that
$C$ be a positive integer such that ![]() $(C, 2d) =1$, and let
$(C, 2d) =1$, and let ![]() $C'$ be the product of all the primes dividing
$C'$ be the product of all the primes dividing ![]() $C$. Let
$C$. Let ![]() $({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; \mathcal {G})$ and assume that:
$({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; \mathcal {G})$ and assume that:
(i)
 $C(\pi )=C$;
$C(\pi )=C$;(ii)
 $\phi _\infty$ is a vector of weight
$\phi _\infty$ is a vector of weight  $k$ in
$k$ in  $\pi _\infty$.
$\pi _\infty$.
Then we have
4.3 The proof of Theorem 4.6
In this subsection, we complete the proof of Theorem 4.6. The case ![]() $\eta _1 = \eta _2$ is a direct corollary of Theorem 1 of [Reference SahaSah20]. So throughout this proof we will assume that
$\eta _1 = \eta _2$ is a direct corollary of Theorem 1 of [Reference SahaSah20]. So throughout this proof we will assume that ![]() $\eta _2 > \eta _1$.
$\eta _2 > \eta _1$.
Let ![]() ${\mathcal {F}}$ be a nice collection that is controlled by
${\mathcal {F}}$ be a nice collection that is controlled by ![]() $(\eta _1, \delta ; \eta _2)$. Let
$(\eta _1, \delta ; \eta _2)$. Let ![]() $({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}}, T)$ be such that
$({\mathbb {C}}\phi , \pi ) \in {\mathcal {A}}(G; {\mathcal {F}}, T)$ be such that ![]() $\langle \phi , \phi \rangle =1$. Furthermore, we assume without loss of generality that
$\langle \phi , \phi \rangle =1$. Furthermore, we assume without loss of generality that ![]() $\phi$ is a weight vector, i.e. there exists some integer
$\phi$ is a weight vector, i.e. there exists some integer ![]() $k$ such that
$k$ such that ![]() $|k| \leqslant T$ and, for all
$|k| \leqslant T$ and, for all ![]() $g \in G({\mathbb {A}})$,
$g \in G({\mathbb {A}})$,
Henceforth, we drop the index ![]() $i$ (since we are dealing with a particular
$i$ (since we are dealing with a particular ![]() $\phi$). Thus, for each prime
$\phi$). Thus, for each prime ![]() $p \in \textbf {S}(\pi )$, the vector
$p \in \textbf {S}(\pi )$, the vector ![]() $v_{i,p}$ occurring in Definition 3.6 is the vector
$v_{i,p}$ occurring in Definition 3.6 is the vector ![]() $\phi _p$ in
$\phi _p$ in ![]() $\pi _p$ in the current setup. We let
$\pi _p$ in the current setup. We let ![]() $\phi '_p$ be the local translate of
$\phi '_p$ be the local translate of ![]() $\phi _p$ that corresponds to
$\phi _p$ that corresponds to ![]() $v'_{i,p}$ from Definition 3.6 for
$v'_{i,p}$ from Definition 3.6 for ![]() $p \in \textbf {S}(\pi )$; we define
$p \in \textbf {S}(\pi )$; we define ![]() $\phi '_p = \phi _p$ for
$\phi '_p = \phi _p$ for ![]() $p \notin \textbf {S}(\pi )$. We let
$p \notin \textbf {S}(\pi )$. We let ![]() $\phi '$ be the automorphic form on
$\phi '$ be the automorphic form on ![]() $G({\mathbb {A}})$ under the fixed isomorphism
$G({\mathbb {A}})$ under the fixed isomorphism ![]() $\pi = \otimes _v \pi _v$. Then the automorphic form
$\pi = \otimes _v \pi _v$. Then the automorphic form ![]() $\phi '$ is just a translate of
$\phi '$ is just a translate of ![]() $\phi$ by a certain element of
$\phi$ by a certain element of ![]() $G({\mathbb {A}}_{\mathbf {f}})$. Therefore,
$G({\mathbb {A}}_{\mathbf {f}})$. Therefore, ![]() $\|\phi '\|_2 = \|\phi \|_2 =1$ and
$\|\phi '\|_2 = \|\phi \|_2 =1$ and ![]() $\sup _{g \in G({\mathbb {A}})}|\phi '(g)| = \sup _{g \in G({\mathbb {A}})}|\phi (g)|$. Henceforth, we will just work with
$\sup _{g \in G({\mathbb {A}})}|\phi '(g)| = \sup _{g \in G({\mathbb {A}})}|\phi (g)|$. Henceforth, we will just work with ![]() $\phi '$.
$\phi '$.
Given some ![]() $p \in \textbf {S}(\pi )$ and some
$p \in \textbf {S}(\pi )$ and some ![]() $\eta _p$ such that
$\eta _p$ such that ![]() $\eta _1 < \eta _p \leqslant \eta _2$, let
$\eta _1 < \eta _p \leqslant \eta _2$, let ![]() ${\mathcal {O}}_p$ and
${\mathcal {O}}_p$ and ![]() ${\mathcal {L}}^{\eta _p}_p$ satisfy the relevant conditions of Definition 3.6. For notational convenience, we henceforth denote
${\mathcal {L}}^{\eta _p}_p$ satisfy the relevant conditions of Definition 3.6. For notational convenience, we henceforth denote ![]() ${\mathcal {L}}_p^{\eta _1} = {\mathcal {O}}_p$ for each
${\mathcal {L}}_p^{\eta _1} = {\mathcal {O}}_p$ for each ![]() $p \in \textbf {S}(\pi )$, so that
$p \in \textbf {S}(\pi )$, so that ![]() ${\mathcal {L}}^{\eta _p}_p$ makes sense for the entire range
${\mathcal {L}}^{\eta _p}_p$ makes sense for the entire range ![]() $\eta _1 \leqslant \eta _p \leqslant \eta _2$.
$\eta _1 \leqslant \eta _p \leqslant \eta _2$.
Let ![]() ${\mathcal {O}}$ be the global order in
${\mathcal {O}}$ be the global order in ![]() $D$ corresponding to the collection of local orders
$D$ corresponding to the collection of local orders ![]() $\{{\mathcal {O}}_p\}_{p \in \textbf {S}(\pi )}$. For any
$\{{\mathcal {O}}_p\}_{p \in \textbf {S}(\pi )}$. For any ![]() $\textbf {S}(\pi )-$tuple
$\textbf {S}(\pi )-$tuple ![]() $H = (\eta _p)_{p \in \textbf {S}(\pi )}$ with each
$H = (\eta _p)_{p \in \textbf {S}(\pi )}$ with each ![]() $\eta _p$ chosen such that
$\eta _p$ chosen such that ![]() $\eta _1 \leqslant \eta _p \leqslant \eta _2$, let
$\eta _1 \leqslant \eta _p \leqslant \eta _2$, let ![]() ${\mathcal {L}}^H$ be the global lattice such that
${\mathcal {L}}^H$ be the global lattice such that ![]() $({\mathcal {L}}^H)_{p} = {\mathcal {L}}^{\eta _p}_p$ if
$({\mathcal {L}}^H)_{p} = {\mathcal {L}}^{\eta _p}_p$ if ![]() $p \in \textbf {S}(\pi )$ and
$p \in \textbf {S}(\pi )$ and ![]() $({\mathcal {L}}^H)_{p} = {\mathcal {O}}^\textrm {max}_p$ if
$({\mathcal {L}}^H)_{p} = {\mathcal {O}}^\textrm {max}_p$ if ![]() $p \notin \textbf {S}(\pi )$. Note that
$p \notin \textbf {S}(\pi )$. Note that ![]() ${\mathcal {L}}^H\subseteq {\mathcal {O}} \subseteq {\mathcal {O}}^\textrm {max}$ and the lattice
${\mathcal {L}}^H\subseteq {\mathcal {O}} \subseteq {\mathcal {O}}^\textrm {max}$ and the lattice ![]() ${}^g{\mathcal {L}}^H$ is tidy in
${}^g{\mathcal {L}}^H$ is tidy in ![]() ${\mathcal {O}}^\textrm {max}$ for all choices of
${\mathcal {O}}^\textrm {max}$ for all choices of ![]() $H$ and all
$H$ and all ![]() $g \in K_{{\mathcal {O}}^\textrm {max}}$. We put
$g \in K_{{\mathcal {O}}^\textrm {max}}$. We put ![]() $N=[{\mathcal {O}}^\textrm {max}: {\mathcal {O}}]$,
$N=[{\mathcal {O}}^\textrm {max}: {\mathcal {O}}]$, ![]() $N^H=[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}^H]$ and note that
$N^H=[{\mathcal {O}}^\textrm {max}: {\mathcal {L}}^H]$ and note that ![]() $N^H=N$ if
$N^H=N$ if ![]() $\eta _p=\eta _1$ for all
$\eta _p=\eta _1$ for all ![]() $p \in \textbf {S}(\pi )$. By our assumptions (see Definition 3.6), we have
$p \in \textbf {S}(\pi )$. By our assumptions (see Definition 3.6), we have
Let ![]() ${\mathcal {J}}$ be a fixed (compact) fundamental domain for the action of
${\mathcal {J}}$ be a fixed (compact) fundamental domain for the action of
on ![]() $\mathbb {H}$. In order to prove Theorem 4.6, it suffices to prove that
$\mathbb {H}$. In order to prove Theorem 4.6, it suffices to prove that
for all ![]() $g = \prod _v g_v \in G({\mathbb {A}})$ satisfying
$g = \prod _v g_v \in G({\mathbb {A}})$ satisfying
This is because any element of ![]() $G({\mathbb {A}})$ can be left multiplied by a suitable element of
$G({\mathbb {A}})$ can be left multiplied by a suitable element of ![]() $Z({\mathbb {A}})G({\mathbb {Q}})$ so that
$Z({\mathbb {A}})G({\mathbb {Q}})$ so that ![]() $g$ has the above property.
$g$ has the above property.
The rest of this subsection is devoted to proving (16).
4.3.1 Test functions
We define a test function ![]() $\kappa$ on
$\kappa$ on ![]() $G({\mathbb {A}})$, which will be essentially the same as the one used in [Reference SahaSah20]. Let
$G({\mathbb {A}})$, which will be essentially the same as the one used in [Reference SahaSah20]. Let ![]() $S = \textbf {S}(\pi ) \cup \{p \in {\mathbf {f}}: p|d\}$. Let
$S = \textbf {S}(\pi ) \cup \{p \in {\mathbf {f}}: p|d\}$. Let ![]() $\textbf {ur} = {\mathbf {f}} \setminus S$ be the set of primes not in
$\textbf {ur} = {\mathbf {f}} \setminus S$ be the set of primes not in ![]() $S$. We will choose
$S$. We will choose ![]() $\kappa$ of the form
$\kappa$ of the form ![]() $\kappa = \kappa _S \kappa _\textbf {ur} \kappa _\infty$. For convenience, we denote
$\kappa = \kappa _S \kappa _\textbf {ur} \kappa _\infty$. For convenience, we denote ![]() $G_S = \prod _{p \in S}G_p$,
$G_S = \prod _{p \in S}G_p$, ![]() ${\mathbb {Q}}_S^\times = \prod _{p \in S} {\mathbb {Q}}_p^\times$, and
${\mathbb {Q}}_S^\times = \prod _{p \in S} {\mathbb {Q}}_p^\times$, and ![]() ${\mathcal {O}}_S^\times = \prod _{p\in S}{\mathcal {O}}_p^\times$. By assumption, the action of
${\mathcal {O}}_S^\times = \prod _{p\in S}{\mathcal {O}}_p^\times$. By assumption, the action of ![]() ${\mathcal {O}}_S^\times$ on
${\mathcal {O}}_S^\times$ on ![]() $\phi '$ generates an irreducible representation of dimension
$\phi '$ generates an irreducible representation of dimension ![]() $\ll _{\epsilon } C_1(\pi )^{\delta + \epsilon }$.
$\ll _{\epsilon } C_1(\pi )^{\delta + \epsilon }$.
We define the function ![]() $\kappa _S$ on
$\kappa _S$ on ![]() $G_S$ as follows:
$G_S$ as follows:
 \[ \kappa_S (g_S)= \begin{cases} 0 & \text{if } g_S \notin {\mathbb{Q}}_S^\times{\mathcal{O}}_S^\times, \\ \omega_{\pi}^{-1}(z) \langle \phi', \pi(k) \phi' \rangle & \text{if } g_S= zk, \quad z \in {\mathbb{Q}}_S^\times,\quad \ k \in {\mathcal{O}}_S^\times. \end{cases} \]
\[ \kappa_S (g_S)= \begin{cases} 0 & \text{if } g_S \notin {\mathbb{Q}}_S^\times{\mathcal{O}}_S^\times, \\ \omega_{\pi}^{-1}(z) \langle \phi', \pi(k) \phi' \rangle & \text{if } g_S= zk, \quad z \in {\mathbb{Q}}_S^\times,\quad \ k \in {\mathcal{O}}_S^\times. \end{cases} \]Then, as in § 4.1 of [Reference SahaSah20], we have
Next we move on to the primes in ![]() $\textbf {ur}$. We define
$\textbf {ur}$. We define ![]() $\kappa _\textbf {ur}$ exactly as in § 4.1 of [Reference SahaSah20]. The definition of
$\kappa _\textbf {ur}$ exactly as in § 4.1 of [Reference SahaSah20]. The definition of ![]() $\kappa _\textbf {ur}$ depends on a parameter
$\kappa _\textbf {ur}$ depends on a parameter ![]() $\Lambda$ that we will fix later. As shown in [Reference SahaSah20],
$\Lambda$ that we will fix later. As shown in [Reference SahaSah20],
Finally, we consider the infinite place. As we are not looking for a bound in the archimedean aspect, the choice of ![]() $\kappa _\infty$ is unimportant. However, for definiteness, let us fix the function
$\kappa _\infty$ is unimportant. However, for definiteness, let us fix the function ![]() $\kappa _\infty$ as follows. Let
$\kappa _\infty$ as follows. Let ![]() $f:{\mathbb {R}}_{\geqslant 0} \rightarrow [0,1]$ be a smooth non-increasing function such that
$f:{\mathbb {R}}_{\geqslant 0} \rightarrow [0,1]$ be a smooth non-increasing function such that ![]() $f(x)=1$ if
$f(x)=1$ if ![]() $x \in [0, \frac 12]$ and
$x \in [0, \frac 12]$ and ![]() $f(x)=0$ if
$f(x)=0$ if ![]() $x \geqslant 1$. Let
$x \geqslant 1$. Let ![]() $g \in \textrm {GL}_2({\mathbb {R}})^+$ and define
$g \in \textrm {GL}_2({\mathbb {R}})^+$ and define ![]() $u(g) = {|g(i) - i|^2}/{4 \,\mathrm {Im}(g(i))}$. Define
$u(g) = {|g(i) - i|^2}/{4 \,\mathrm {Im}(g(i))}$. Define
for ![]() $g \in \textrm {GL}_2({\mathbb {R}})^+$ and define
$g \in \textrm {GL}_2({\mathbb {R}})^+$ and define ![]() $\kappa _\infty$ to be equal to identically zero on
$\kappa _\infty$ to be equal to identically zero on ![]() $\textrm {GL}_2({\mathbb {R}})^-$. Then we have that
$\textrm {GL}_2({\mathbb {R}})^-$. Then we have that
and furthermore the operator ![]() $R(\kappa _\infty )$ satisfies
$R(\kappa _\infty )$ satisfies
We define the automorphic kernel ![]() $K_\kappa (g_1, g_2)$ for
$K_\kappa (g_1, g_2)$ for ![]() $g_1, g_2 \in G({\mathbb {A}})$ via
$g_1, g_2 \in G({\mathbb {A}})$ via
Now, as in § 4.2 of [Reference SahaSah20], we get
On the other hand, we have by construction
 \begin{equation} K_\kappa(g,g) \leqslant \sum_{1 \leqslant \ell \leqslant 16\Lambda^4} \frac{y_\ell}{\ell^{1/2}}\sum_{\substack{\gamma \in G'({\mathbb{Q}})\\ \kappa_\ell(\gamma) \neq 0 \\ \kappa_\infty(g_\infty^{-1}\gamma_\infty g_\infty) \neq 0} } \big|\kappa_S(g_S^{-1}\gamma_S g_S) \big|, \end{equation}
\begin{equation} K_\kappa(g,g) \leqslant \sum_{1 \leqslant \ell \leqslant 16\Lambda^4} \frac{y_\ell}{\ell^{1/2}}\sum_{\substack{\gamma \in G'({\mathbb{Q}})\\ \kappa_\ell(\gamma) \neq 0 \\ \kappa_\infty(g_\infty^{-1}\gamma_\infty g_\infty) \neq 0} } \big|\kappa_S(g_S^{-1}\gamma_S g_S) \big|, \end{equation}
where the ![]() $y_\ell$ satisfy
$y_\ell$ satisfy
 \begin{equation} |y_\ell| \ll \begin{cases}\Lambda, & \ell=1,\\1, & \ell = \ell_1 \ell_2 \text{ or } \ell = \ell_1^2\ell_2^2 \text{ with } \ell_1, \ell_2 \in \mathcal{P}, \\ 0, & \text{otherwise}\end{cases}\end{equation}
\begin{equation} |y_\ell| \ll \begin{cases}\Lambda, & \ell=1,\\1, & \ell = \ell_1 \ell_2 \text{ or } \ell = \ell_1^2\ell_2^2 \text{ with } \ell_1, \ell_2 \in \mathcal{P}, \\ 0, & \text{otherwise}\end{cases}\end{equation}
with ![]() $\mathcal {P}= \{\ell : \ell \text { prime, } \ell \in \textbf {ur}, \ \Lambda \leqslant \ell \leqslant 2\Lambda \}$ and where
$\mathcal {P}= \{\ell : \ell \text { prime, } \ell \in \textbf {ur}, \ \Lambda \leqslant \ell \leqslant 2\Lambda \}$ and where ![]() $\kappa _\ell = \prod _{p \in \textbf {ur}}\kappa _{\ell , p}$ is a function on
$\kappa _\ell = \prod _{p \in \textbf {ur}}\kappa _{\ell , p}$ is a function on ![]() $\prod _{p \in \textbf {ur}} G({\mathbb {Q}}_p)$ that is defined in § 3.5 of [Reference SahaSah17] (see also § 4.1 of [Reference SahaSah20]); we recall that
$\prod _{p \in \textbf {ur}} G({\mathbb {Q}}_p)$ that is defined in § 3.5 of [Reference SahaSah17] (see also § 4.1 of [Reference SahaSah20]); we recall that ![]() $\kappa _{\ell , p}$ is supported on
$\kappa _{\ell , p}$ is supported on ![]() ${\mathbb {Q}}_p^\times {\mathcal {O}}_p(\ell )$, where
${\mathbb {Q}}_p^\times {\mathcal {O}}_p(\ell )$, where ![]() ${\mathcal {O}}_p(\ell ) = \{ \alpha \in {\mathcal {O}}_p: \textrm {nr}(\alpha ) \in \ell {\mathbb {Z}}_p^\times \}$.
${\mathcal {O}}_p(\ell ) = \{ \alpha \in {\mathcal {O}}_p: \textrm {nr}(\alpha ) \in \ell {\mathbb {Z}}_p^\times \}$.
Let us look at (22) more carefully. First of all, note that if ![]() $\kappa _\ell (\gamma ) \kappa _\infty (g_\infty ^{-1}\gamma _\infty g_\infty ) \neq 0$, then:
$\kappa _\ell (\gamma ) \kappa _\infty (g_\infty ^{-1}\gamma _\infty g_\infty ) \neq 0$, then:
(a)
 $\gamma _p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p(\ell ) \quad \forall p \in \textbf {ur}$;
$\gamma _p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p(\ell ) \quad \forall p \in \textbf {ur}$;(b)
 $\det (\iota _\infty (\gamma _\infty ))>0$,
$\det (\iota _\infty (\gamma _\infty ))>0$,  $u(z, \iota _\infty (\gamma _\infty ) z) \leqslant 1$, where
$u(z, \iota _\infty (\gamma _\infty ) z) \leqslant 1$, where  $z = g_\infty i$.
$z = g_\infty i$.
Looking at the primes ![]() $p |d$, we see that
$p |d$, we see that ![]() $\kappa _S(g_S^{-1}\gamma _S g_S) \neq 0$ implies that:
$\kappa _S(g_S^{-1}\gamma _S g_S) \neq 0$ implies that:
(c)
 $\gamma _p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p^\times \quad \forall p |d$.
$\gamma _p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p^\times \quad \forall p |d$.
(We remind the reader here that ![]() ${\mathcal {O}}_p = {\mathcal {O}}^\textrm {max}_p$ if
${\mathcal {O}}_p = {\mathcal {O}}^\textrm {max}_p$ if ![]() $p \in \textbf {ur}$ or if
$p \in \textbf {ur}$ or if ![]() $p|d$.)
$p|d$.)
Consider the primes ![]() $p \in \textbf {S}(\pi )$. If
$p \in \textbf {S}(\pi )$. If ![]() $\kappa _p(g_p^{-1}\gamma _p g_p) \neq 0$, then clearly
$\kappa _p(g_p^{-1}\gamma _p g_p) \neq 0$, then clearly ![]() $g_p^{-1}\gamma _p g_p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p^\times$ or, equivalently,
$g_p^{-1}\gamma _p g_p \in {\mathbb {Q}}_p^\times {\mathcal {O}}_p^\times$ or, equivalently, ![]() $\gamma _p \in {\mathbb {Q}}_p^\times ({}^g{\mathcal {O}})_p^\times$. So far, we have not at all used condition
$\gamma _p \in {\mathbb {Q}}_p^\times ({}^g{\mathcal {O}})_p^\times$. So far, we have not at all used condition ![]() $(2)$ of Definition 3.6. We now do so. For each prime
$(2)$ of Definition 3.6. We now do so. For each prime ![]() $p \in \textbf {S}(\pi )$, define
$p \in \textbf {S}(\pi )$, define ![]() $r_p = a_1(\pi _p)+1.$ Define
$r_p = a_1(\pi _p)+1.$ Define ![]() $R_p = \{1, \ldots , r_p\}$ and let
$R_p = \{1, \ldots , r_p\}$ and let ![]() $R$ be the set-theoretic product
$R$ be the set-theoretic product ![]() $\prod _{p \in \textbf {S}(\pi )}R_p$. For each
$\prod _{p \in \textbf {S}(\pi )}R_p$. For each ![]() $u = (u_p)_{p\in \textbf {S}(\pi )} \in R$, where each
$u = (u_p)_{p\in \textbf {S}(\pi )} \in R$, where each ![]() $u_p \in R_p$, associate another tuple
$u_p \in R_p$, associate another tuple ![]() $H_u = (\eta _{p,u_p})_{p\in \textbf {S}(\pi )}$ as follows:
$H_u = (\eta _{p,u_p})_{p\in \textbf {S}(\pi )}$ as follows: ![]() $\eta _{p, 1} = \eta _1$ and
$\eta _{p, 1} = \eta _1$ and ![]() $\eta _{p,i} = \eta _1 + (i-1) (({\eta _2-\eta _1})/{a_1(\pi _p))}$ for all
$\eta _{p,i} = \eta _1 + (i-1) (({\eta _2-\eta _1})/{a_1(\pi _p))}$ for all ![]() $1\leqslant i \leqslant r_p$.
$1\leqslant i \leqslant r_p$.
Now consider a ![]() $\gamma \in G'({\mathbb {Q}})$ which satisfies (a)–(c) above and such that
$\gamma \in G'({\mathbb {Q}})$ which satisfies (a)–(c) above and such that ![]() $\gamma _p \in {\mathbb {Q}}_p^\times ({}^g{\mathcal {O}})_p^\times$ for each
$\gamma _p \in {\mathbb {Q}}_p^\times ({}^g{\mathcal {O}})_p^\times$ for each ![]() $p \in \textbf {S}(\pi )$. It is clear that for any such
$p \in \textbf {S}(\pi )$. It is clear that for any such ![]() $\gamma$, there exists a unique tuple
$\gamma$, there exists a unique tuple ![]() $u \in R$ such that:
$u \in R$ such that:
(d)
 $g_p^{-1}\gamma _p g_p \in {\mathbb {Q}}_p^\times ({\mathcal {L}}^{\eta _{p,u_p}}_p \cap {\mathcal {O}}_p^\times )$,
$g_p^{-1}\gamma _p g_p \in {\mathbb {Q}}_p^\times ({\mathcal {L}}^{\eta _{p,u_p}}_p \cap {\mathcal {O}}_p^\times )$,  $g_p^{-1}\gamma _p g_p \notin {\mathbb {Q}}_p^\times ({\mathcal {L}}^{\eta _{p,u_p+1}}_p \cap {\mathcal {O}}_p^\times ) \quad \forall p \in \textbf {S}(\pi )$.
$g_p^{-1}\gamma _p g_p \notin {\mathbb {Q}}_p^\times ({\mathcal {L}}^{\eta _{p,u_p+1}}_p \cap {\mathcal {O}}_p^\times ) \quad \forall p \in \textbf {S}(\pi )$.
Above, we adopt the convention that ![]() ${\mathcal {L}}_p^{\eta _{p,r_p+1}}$ is the empty set for each
${\mathcal {L}}_p^{\eta _{p,r_p+1}}$ is the empty set for each ![]() $p \in \textbf {S}(\pi )$, so that the second part of condition (d) is automatic for the primes where
$p \in \textbf {S}(\pi )$, so that the second part of condition (d) is automatic for the primes where ![]() $u_p=r_p$.
$u_p=r_p$.
It is clear from the above discussion that the contribution to the right-most sum in (22) only comes from those ![]() $\gamma$ for which the conditions (a)–(d) above are satisfied for some tuple
$\gamma$ for which the conditions (a)–(d) above are satisfied for some tuple ![]() $u \in R$. Furthermore, whenever the conditions (a)–(d) above are satisfied for a particular
$u \in R$. Furthermore, whenever the conditions (a)–(d) above are satisfied for a particular ![]() $u$, condition 2(c) of Definition 3.6 implies that
$u$, condition 2(c) of Definition 3.6 implies that
For each tuple ![]() $u$, recall the definition of the lattice
$u$, recall the definition of the lattice ![]() ${\mathcal {L}}^{H_u}$, which is precisely the global lattice corresponding to the collection of local lattices
${\mathcal {L}}^{H_u}$, which is precisely the global lattice corresponding to the collection of local lattices ![]() $\{{\mathcal {L}}_p^{\eta _{p,u_p}}\}_{p\in \textbf {S}(\pi )}$. Define
$\{{\mathcal {L}}_p^{\eta _{p,u_p}}\}_{p\in \textbf {S}(\pi )}$. Define
By Proposition 4.2 of [Reference SahaSah20], the number of ![]() $\gamma \in G'({\mathbb {Q}})$ satisfying (a)–(d) above is bounded by the size of
$\gamma \in G'({\mathbb {Q}})$ satisfying (a)–(d) above is bounded by the size of ![]() $|{}^g{\mathcal {L}}^{H_u}(\ell ;z, 1)|$.
$|{}^g{\mathcal {L}}^{H_u}(\ell ;z, 1)|$.
Therefore, we conclude that
Now, using the facts that the lattice ![]() ${}^g{\mathcal {L}}^{H_u}$ is tidy in
${}^g{\mathcal {L}}^{H_u}$ is tidy in ![]() ${\mathcal {O}}^\textrm {max}$ and has index
${\mathcal {O}}^\textrm {max}$ and has index ![]() $N^{H_u}$ in
$N^{H_u}$ in ![]() ${\mathcal {O}}^\textrm {max}$, we use Proposition 2.1 and (15) to obtain for each
${\mathcal {O}}^\textrm {max}$, we use Proposition 2.1 and (15) to obtain for each ![]() $1 \leqslant L \leqslant C(\pi )^{O(1)}$,
$1 \leqslant L \leqslant C(\pi )^{O(1)}$,
 \begin{gather} \sum_{1\leqslant m \leqslant L } |{}^g{\mathcal{L}}^{H_u}(m;z, 1)| \ll_{\epsilon} C(\pi)^{\epsilon} \biggl( L +C'(\pi)^{O(1)}\frac{L^2}{N\prod_{p \in \textbf{S}(\pi)} p^{(\eta_2 - \eta_1)(u_p - 1)} } \biggr), \end{gather}
\begin{gather} \sum_{1\leqslant m \leqslant L } |{}^g{\mathcal{L}}^{H_u}(m;z, 1)| \ll_{\epsilon} C(\pi)^{\epsilon} \biggl( L +C'(\pi)^{O(1)}\frac{L^2}{N\prod_{p \in \textbf{S}(\pi)} p^{(\eta_2 - \eta_1)(u_p - 1)} } \biggr), \end{gather} \begin{gather} \sum_{1\leqslant m \leqslant L } |{}^g{\mathcal{L}}^{H_u}(m^2;z, 1)| \ll_{\epsilon}C(\pi)^{\epsilon} \biggl( L +C'(\pi)^{O(1)}\frac{L^3}{N\prod_{p \in \textbf{S}(\pi)} p^{(\eta_2 - \eta_1)(u_p - 1)} } \biggr). \end{gather}
\begin{gather} \sum_{1\leqslant m \leqslant L } |{}^g{\mathcal{L}}^{H_u}(m^2;z, 1)| \ll_{\epsilon}C(\pi)^{\epsilon} \biggl( L +C'(\pi)^{O(1)}\frac{L^3}{N\prod_{p \in \textbf{S}(\pi)} p^{(\eta_2 - \eta_1)(u_p - 1)} } \biggr). \end{gather}Combining (23), (24), (25), and (26), we get
 \begin{align} K_\kappa(g,g) &\ll_{ \epsilon} C'(\pi)^{O(1)}C(\pi)^{\epsilon} \biggl(\Lambda + \frac{\Lambda^4}{NC_1(\pi)^{\eta_2-\eta_1}}\biggr) \sum_{u\in R } 1 \nonumber\\ &\ll_\epsilon C'(\pi)^{O(1)} C(\pi)^\epsilon \biggl(\Lambda + \frac{\Lambda^4}{NC_1(\pi)^{\eta_2-\eta_1}}\biggr) \end{align}
\begin{align} K_\kappa(g,g) &\ll_{ \epsilon} C'(\pi)^{O(1)}C(\pi)^{\epsilon} \biggl(\Lambda + \frac{\Lambda^4}{NC_1(\pi)^{\eta_2-\eta_1}}\biggr) \sum_{u\in R } 1 \nonumber\\ &\ll_\epsilon C'(\pi)^{O(1)} C(\pi)^\epsilon \biggl(\Lambda + \frac{\Lambda^4}{NC_1(\pi)^{\eta_2-\eta_1}}\biggr) \end{align}
since ![]() $|R| \ll _\epsilon C(\pi )^\epsilon$.
$|R| \ll _\epsilon C(\pi )^\epsilon$.
From (21) and (27), we obtain the pivotal inequality
Now, putting ![]() $\Lambda = C_1(\pi )^{{\eta _2}/3}$, we immediately obtain (16), as required.
$\Lambda = C_1(\pi )^{{\eta _2}/3}$, we immediately obtain (16), as required.
5. Some  $p$-adic stationary phase analysis
$p$-adic stationary phase analysis
This section will be purely local. The results here will complete the proof of Proposition 3.14.
5.1 Notation
The following notation will be used throughout § 5. We let ![]() $F$ be a non-archimedean local field of characteristic zero. We assume throughout that
$F$ be a non-archimedean local field of characteristic zero. We assume throughout that ![]() $F$ has odd residue cardinality
$F$ has odd residue cardinality ![]() $q$. Let
$q$. Let ![]() $\mathfrak {o}$ be its ring of integers and
$\mathfrak {o}$ be its ring of integers and ![]() $\mathfrak {p}$ its maximal ideal. Fix a uniformizer
$\mathfrak {p}$ its maximal ideal. Fix a uniformizer ![]() $\varpi$ of
$\varpi$ of ![]() ${\mathfrak o}$ (a choice of generator of
${\mathfrak o}$ (a choice of generator of ![]() $\mathfrak {p}$). Let
$\mathfrak {p}$). Let ![]() $|.|$ denote the absolute value on
$|.|$ denote the absolute value on ![]() $F$ normalized so that
$F$ normalized so that ![]() $|\varpi | = q^{-1}$. For each
$|\varpi | = q^{-1}$. For each ![]() $x \in F^\times$, let
$x \in F^\times$, let ![]() $v(x)$ denote the integer such that
$v(x)$ denote the integer such that ![]() $|x| = q^{-v(x)}$. For a non-negative integer
$|x| = q^{-v(x)}$. For a non-negative integer ![]() $m$, we define the subgroup
$m$, we define the subgroup ![]() $U_m$ of
$U_m$ of ![]() ${\mathfrak o}^\times$ to be the set of elements
${\mathfrak o}^\times$ to be the set of elements ![]() $x \in {\mathfrak o}^\times$ such that
$x \in {\mathfrak o}^\times$ such that ![]() $v(x-1) \geqslant m$.
$v(x-1) \geqslant m$.
Let ![]() $\psi$ be a fixed non-trivial additive character of
$\psi$ be a fixed non-trivial additive character of ![]() $F$ and let
$F$ and let ![]() $a(\psi )$ be the smallest integer such that
$a(\psi )$ be the smallest integer such that ![]() $\psi$ is trivial on
$\psi$ is trivial on ![]() $\mathfrak p^{a(\psi )}$. For
$\mathfrak p^{a(\psi )}$. For ![]() $\chi$ a multiplicative character of
$\chi$ a multiplicative character of ![]() $F$, let
$F$, let ![]() $a(\chi )$ be the smallest integer such that
$a(\chi )$ be the smallest integer such that ![]() $\chi$ is trivial on
$\chi$ is trivial on ![]() $U_{a(\chi )}$. We recall the following well-known lemma (see, e.g., Lemma 2.37 of [Reference SahaSah16]).
$U_{a(\chi )}$. We recall the following well-known lemma (see, e.g., Lemma 2.37 of [Reference SahaSah16]).
Lemma 5.1 Let ![]() $\chi$ be a multiplicative character over
$\chi$ be a multiplicative character over ![]() $F$ with
$F$ with ![]() $a(\chi )\geqslant 2$. Then there exists
$a(\chi )\geqslant 2$. Then there exists ![]() $\alpha _\chi \in F^\times$ such that
$\alpha _\chi \in F^\times$ such that ![]() $v(\alpha _\chi )=-a(\chi )+a(\psi )$ and
$v(\alpha _\chi )=-a(\chi )+a(\psi )$ and
for any ![]() ${{\Delta }} x\in \mathfrak p^{\lceil a(\chi )/2\rceil }$.
${{\Delta }} x\in \mathfrak p^{\lceil a(\chi )/2\rceil }$.
Throughout this section, we denote ![]() ${\mathcal {O}} = M_2({\mathfrak o})$,
${\mathcal {O}} = M_2({\mathfrak o})$, ![]() $G = \textrm {GL}_2(F)$, and
$G = \textrm {GL}_2(F)$, and ![]() $K=\textrm {GL}_2({\mathfrak o})$. Define subgroups
$K=\textrm {GL}_2({\mathfrak o})$. Define subgroups ![]() $N = \{n(x): x\in F \}$,
$N = \{n(x): x\in F \}$, ![]() $A = \{a(y): y\in F^\times \}$,
$A = \{a(y): y\in F^\times \}$, ![]() $Z =\{ z(t): t \in F^\times \}$,
$Z =\{ z(t): t \in F^\times \}$, ![]() $B_1=NA$, and
$B_1=NA$, and ![]() $B = Z N A = G \cap [ \begin {smallmatrix} * & *\\ & * \end {smallmatrix} ]$ of
$B = Z N A = G \cap [ \begin {smallmatrix} * & *\\ & * \end {smallmatrix} ]$ of ![]() $G$. For each non-negative integer
$G$. For each non-negative integer ![]() $r$,
$r$, ![]() $s$, denote
$s$, denote
 \begin{gather*} K_0(r) = K \cap \begin{pmatrix} * & * \\ \mathfrak p^r & * \end{pmatrix},\quad K^\ast(r,s) = K \cap \begin{pmatrix} \ast & \mathfrak p^s \\ \mathfrak p^r & \ast \end{pmatrix},\\ \quad {\mathcal{O}}(r) = {\mathcal{O}} \cap \begin{pmatrix} \ast & \mathfrak p^r \\ \mathfrak p^r & \ast \end{pmatrix}, \quad K^\ast(r)= K^\ast(r,r) = ({\mathcal{O}}(r))^\times. \end{gather*}
\begin{gather*} K_0(r) = K \cap \begin{pmatrix} * & * \\ \mathfrak p^r & * \end{pmatrix},\quad K^\ast(r,s) = K \cap \begin{pmatrix} \ast & \mathfrak p^s \\ \mathfrak p^r & \ast \end{pmatrix},\\ \quad {\mathcal{O}}(r) = {\mathcal{O}} \cap \begin{pmatrix} \ast & \mathfrak p^r \\ \mathfrak p^r & \ast \end{pmatrix}, \quad K^\ast(r)= K^\ast(r,r) = ({\mathcal{O}}(r))^\times. \end{gather*} We note our normalization of Haar measures. The measure ![]() $dx$ on the additive group
$dx$ on the additive group ![]() $F$ assigns volume 1 to
$F$ assigns volume 1 to ![]() ${\mathfrak o}$ and transports to a measure on
${\mathfrak o}$ and transports to a measure on ![]() $N$. The measure
$N$. The measure ![]() $d^\times y$ on the multiplicative group
$d^\times y$ on the multiplicative group ![]() $F^\times$ assigns volume 1 to
$F^\times$ assigns volume 1 to ![]() ${\mathfrak o}^\times$ and transports to measures on
${\mathfrak o}^\times$ and transports to measures on ![]() $A$ and
$A$ and ![]() $Z$. We obtain a left Haar measure
$Z$. We obtain a left Haar measure ![]() $d_Lb$ on
$d_Lb$ on ![]() $B$ via
$B$ via ![]() $d_L(z(u)n(x)a(y)) = |y|^{-1}\, d^\times u \, dx\, d^\times y.$ Let
$d_L(z(u)n(x)a(y)) = |y|^{-1}\, d^\times u \, dx\, d^\times y.$ Let ![]() $dk$ be the probability Haar measure on
$dk$ be the probability Haar measure on ![]() $K$. The Iwasawa decomposition
$K$. The Iwasawa decomposition ![]() $G = B K$ gives a left Haar measure
$G = B K$ gives a left Haar measure ![]() $dg = d_L b \, d k$ on
$dg = d_L b \, d k$ on ![]() $G$.
$G$.
Let ![]() $\pi$ be an irreducible, infinite-dimensional, unitary representation of
$\pi$ be an irreducible, infinite-dimensional, unitary representation of ![]() $G$ with trivial central character. We define
$G$ with trivial central character. We define ![]() $a(\pi )$ to be the smallest non-negative integer such that
$a(\pi )$ to be the smallest non-negative integer such that ![]() $\pi$ has a
$\pi$ has a ![]() $K_0(a(\pi ))$-fixed vector. Let
$K_0(a(\pi ))$-fixed vector. Let ![]() $\langle , \rangle$ denote a
$\langle , \rangle$ denote a ![]() $G$-invariant inner product on
$G$-invariant inner product on ![]() $V_\pi$ (which is unique up to multiples).
$V_\pi$ (which is unique up to multiples).
We will use the following notation:
–
 $n =a(\pi )$;
$n =a(\pi )$;–
 $n_1 := \lceil \frac{n}{2} \rceil$;
$n_1 := \lceil \frac{n}{2} \rceil$;–
 $n_0:= n -n_1 = \lfloor \frac{n}{2} \rfloor$.
$n_0:= n -n_1 = \lfloor \frac{n}{2} \rfloor$.
We let ![]() $v_\pi$ denote a newform in the space of
$v_\pi$ denote a newform in the space of ![]() $\pi$, i.e. a non-zero vector fixed by
$\pi$, i.e. a non-zero vector fixed by ![]() $K_0(\mathfrak p^n)$; it is known that
$K_0(\mathfrak p^n)$; it is known that ![]() $v_\pi$ is unique up to multiples. Put
$v_\pi$ is unique up to multiples. Put ![]() $v_\pi ' = \pi (a(\varpi ^{n_1}))v_\pi$. Note that
$v_\pi ' = \pi (a(\varpi ^{n_1}))v_\pi$. Note that ![]() $v_\pi '$ is the unique (up to multiples) non-zero vector in
$v_\pi '$ is the unique (up to multiples) non-zero vector in ![]() $\pi$ that is invariant under the subgroup
$\pi$ that is invariant under the subgroup ![]() $a(\varpi ^{n_1})K_0(n)a(\varpi ^{-n_1})$. Define matrix coefficients
$a(\varpi ^{n_1})K_0(n)a(\varpi ^{-n_1})$. Define matrix coefficients ![]() $\Phi _\pi$,
$\Phi _\pi$, ![]() $\Phi _\pi '$ on
$\Phi _\pi '$ on ![]() $G$ as follows:
$G$ as follows:
 \begin{gather*} \Phi_\pi(g) = \frac{\langle v_\pi , \pi(g) v_\pi\rangle}{\langle v_\pi , v_\pi\rangle},\\ \Phi_\pi'(g) = \Phi_\pi(a(\varpi^{-n_1})ga(\varpi^{n_1})) = \frac{\langle v_\pi' , \pi(g) v_\pi'\rangle}{\langle v_\pi' , v_\pi'\rangle}. \end{gather*}
\begin{gather*} \Phi_\pi(g) = \frac{\langle v_\pi , \pi(g) v_\pi\rangle}{\langle v_\pi , v_\pi\rangle},\\ \Phi_\pi'(g) = \Phi_\pi(a(\varpi^{-n_1})ga(\varpi^{n_1})) = \frac{\langle v_\pi' , \pi(g) v_\pi'\rangle}{\langle v_\pi' , v_\pi'\rangle}. \end{gather*}
These definitions are independent of the choice of ![]() $v_\pi$ or of the inner product.
$v_\pi$ or of the inner product.
5.2 A reformulation of Proposition 3.14
For the rest of § 5, let ![]() $\pi$,
$\pi$, ![]() $v_\pi$,
$v_\pi$, ![]() $v_\pi '$,
$v_\pi '$, ![]() $\Phi _\pi '$ be as above and assume that
$\Phi _\pi '$ be as above and assume that ![]() $a(\pi )>2$ and
$a(\pi )>2$ and ![]() $\pi$ has trivial central character. This is sufficient for the purpose of proving Theorem 3.14, as noted in Remark 3.16.
$\pi$ has trivial central character. This is sufficient for the purpose of proving Theorem 3.14, as noted in Remark 3.16.
Proposition 5.2 For each representation ![]() $\pi$ as above, the following hold.
$\pi$ as above, the following hold.
(a) The subrepresentation of
 $\pi |_{K^\ast (1)}$ generated by
$\pi |_{K^\ast (1)}$ generated by  $v_\pi '$ is irreducible of dimension
$v_\pi '$ is irreducible of dimension  $\ll q^{n_0}$.
$\ll q^{n_0}$.(b) Let
 $j \leqslant n_1$. Then, for all
$j \leqslant n_1$. Then, for all  $g \in K^\ast (1)$,
$g \in K^\ast (1)$,  $g \notin K^\ast (j+1)$, we have
$g \notin K^\ast (j+1)$, we have  $|\Phi _\pi '(g)| \ll q^{({j-n_1})/{2} + O(1)}$.
$|\Phi _\pi '(g)| \ll q^{({j-n_1})/{2} + O(1)}$.
Before starting on the proof of Proposition 5.2, we explain how it implies Proposition 3.14.
Proof that Proposition 5.2 implies Proposition 3.14 Let ![]() $\eta _1 = 0$,
$\eta _1 = 0$, ![]() $\eta _2 =1/2$,
$\eta _2 =1/2$, ![]() $\delta =1$. Let
$\delta =1$. Let ![]() $p$ be an odd prime not dividing
$p$ be an odd prime not dividing ![]() $d$ and consider Proposition 5.2 with
$d$ and consider Proposition 5.2 with ![]() $F={\mathbb {Q}}_p$. We need to show that the conditions (1) and (2) of Definition 3.6 hold. In the context of Definition 3.6,
$F={\mathbb {Q}}_p$. We need to show that the conditions (1) and (2) of Definition 3.6 hold. In the context of Definition 3.6, ![]() $\pi _{i,p} = \pi$,
$\pi _{i,p} = \pi$, ![]() $v_{i,p}=v_\pi$, where
$v_{i,p}=v_\pi$, where ![]() $\pi$ and
$\pi$ and ![]() $v_\pi$ are as defined in the beginning of this section. We define
$v_\pi$ are as defined in the beginning of this section. We define ![]() $g_{i,p} = \iota _p^{-1}\big (\begin {smallmatrix}{\varpi ^{a_1(\pi _i)}} & {}\\ {} & {1}\end {smallmatrix}\big )$ and
$g_{i,p} = \iota _p^{-1}\big (\begin {smallmatrix}{\varpi ^{a_1(\pi _i)}} & {}\\ {} & {1}\end {smallmatrix}\big )$ and ![]() ${\mathcal {O}}_{i,p} = \iota _p^{-1}({\mathcal {O}}(1))$. The vector
${\mathcal {O}}_{i,p} = \iota _p^{-1}({\mathcal {O}}(1))$. The vector ![]() $v_{i,p}'$ from Definition 3.6 is then the vector
$v_{i,p}'$ from Definition 3.6 is then the vector ![]() $v_\pi '$ defined above. Now condition (1) of Definition 3.6 follows immediately from part (a) of Proposition 5.2.
$v_\pi '$ defined above. Now condition (1) of Definition 3.6 follows immediately from part (a) of Proposition 5.2.
In order to verify condition (2), let ![]() $0 \leqslant \eta \leqslant \frac 12$. Define
$0 \leqslant \eta \leqslant \frac 12$. Define ![]() $j = \lfloor n_1 \eta /2 \rfloor$ and put
$j = \lfloor n_1 \eta /2 \rfloor$ and put ![]() ${\mathcal {L}}^\eta _{i,p} = \iota _p^{-1} ({\mathcal {O}}(j+1))$. Now condition (2) of Definition 3.6 is an immediate consequence of part (b) of Proposition 5.2.
${\mathcal {L}}^\eta _{i,p} = \iota _p^{-1} ({\mathcal {O}}(j+1))$. Now condition (2) of Definition 3.6 is an immediate consequence of part (b) of Proposition 5.2.
Remark 5.3 For the purpose of verifying condition (2) in the proof above, we could have selected ![]() $j$ to be any non-decreasing integer-valued function of
$j$ to be any non-decreasing integer-valued function of ![]() $\eta \in [0, \frac 12]$ satisfying
$\eta \in [0, \frac 12]$ satisfying ![]() ${n_1 \eta }/{2} - O(1) \leqslant j \leqslant 2n_1 \eta + O(1)$.
${n_1 \eta }/{2} - O(1) \leqslant j \leqslant 2n_1 \eta + O(1)$.
5.3 Proof of part (a) of Proposition 5.2
Let us prove part (a) of Proposition 5.2. Let ![]() $V_1$ be the vector space generated by the action of
$V_1$ be the vector space generated by the action of ![]() $K^\ast (1)$ on
$K^\ast (1)$ on ![]() $v_\pi '$. First we show that the action of
$v_\pi '$. First we show that the action of ![]() $K^\ast (1)$ on
$K^\ast (1)$ on ![]() $V_1$ is irreducible. If not, then there exists a direct sum decomposition
$V_1$ is irreducible. If not, then there exists a direct sum decomposition ![]() $V_1 = V_2 + V_3$ into non-zero subspaces
$V_1 = V_2 + V_3$ into non-zero subspaces ![]() $V_2$ and
$V_2$ and ![]() $V_3$ which each admit an action of
$V_3$ which each admit an action of ![]() $K^\ast (1)$. Since
$K^\ast (1)$. Since ![]() $v_\pi '$ generates
$v_\pi '$ generates ![]() $V_1$, its projections along
$V_1$, its projections along ![]() $V_2$ and
$V_2$ and ![]() $V_3$ give two linearly independent vectors which are both fixed by the subgroup
$V_3$ give two linearly independent vectors which are both fixed by the subgroup ![]() $a(\varpi ^{n_1})K_0(n)a(\varpi ^{-n_1}) \subseteq K^\ast (1)$ (recall that
$a(\varpi ^{n_1})K_0(n)a(\varpi ^{-n_1}) \subseteq K^\ast (1)$ (recall that ![]() $a(\pi ) \geqslant 2$). This contradicts newform theory, thus showing the irreducibility of
$a(\pi ) \geqslant 2$). This contradicts newform theory, thus showing the irreducibility of ![]() $V_1$.
$V_1$.
Next, we need to show that ![]() $\mathrm {dim}(V_1) \ll q^{n_1}$. Let
$\mathrm {dim}(V_1) \ll q^{n_1}$. Let ![]() $V_2$ be the vector space generated by the action of
$V_2$ be the vector space generated by the action of ![]() $K^\ast (0,n_1-n_0)$ on
$K^\ast (0,n_1-n_0)$ on ![]() $v_\pi '$. Since
$v_\pi '$. Since ![]() $K^\ast (1)$ is a subgroup of
$K^\ast (1)$ is a subgroup of ![]() $K^\ast (0,n_1-n_0)$, it follows that
$K^\ast (0,n_1-n_0)$, it follows that ![]() $\mathrm {dim}(V_1) \leqslant \mathrm {dim}(V_2)$. On the other hand, Proposition 2.13 and Lemma 2.18 of [Reference SahaSah17] show that
$\mathrm {dim}(V_1) \leqslant \mathrm {dim}(V_2)$. On the other hand, Proposition 2.13 and Lemma 2.18 of [Reference SahaSah17] show that ![]() $\mathrm {dim}(V_2) \ll q^{n_0}.$ This completes the proof.
$\mathrm {dim}(V_2) \ll q^{n_0}.$ This completes the proof.
5.4 A refinement of part (b)
In this subsection, we state a refinement of assertion (b) of Proposition 5.2 in terms of a theorem that involves the matrix coefficient associated to the newvector.
Theorem 5.4 Let ![]() $y$,
$y$, ![]() $z$ in
$z$ in ![]() $F^\times$ and
$F^\times$ and ![]() $m \in F$.
$m \in F$.
(i) Suppose that
 $n_0 < i < n-1$. Then we have
(30)and, furthermore, for such
$n_0 < i < n-1$. Then we have
(30)and, furthermore, for such \begin{equation} \bigg|\Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg)\bigg| \ll q^{({i-n})/{2} + O(1)} \end{equation}
\begin{equation} \bigg|\Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg)\bigg| \ll q^{({i-n})/{2} + O(1)} \end{equation} $i$ as above, we have
(31)
$i$ as above, we have
(31) \begin{equation} \Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg) \neq 0 \Rightarrow v(y)=v(z)=v(m)+n-i. \end{equation}
\begin{equation} \Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg) \neq 0 \Rightarrow v(y)=v(z)=v(m)+n-i. \end{equation}(ii) Suppose that
 $n-1 \leqslant i \leqslant n$. Then we have
(32)
$n-1 \leqslant i \leqslant n$. Then we have
(32) \begin{equation} \Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg) \neq 0 \Rightarrow v(y)=v(z)\leqslant v(m)+1. \end{equation}
\begin{equation} \Phi_\pi\bigg( \bigg( {\matrix{ y & m \cr 0 & z \cr } } \bigg)\bigg( {\matrix{ 1 & 0 \cr {\varpi^i} & 1 \cr } } \bigg)\bigg) \neq 0 \Rightarrow v(y)=v(z)\leqslant v(m)+1. \end{equation}
Before starting on the proof of Theorem 5.4, we explain how it implies Proposition 5.2.
Proof that Theorem 5.4 implies Proposition 5.2 Let ![]() $j$,
$j$, ![]() $g$ be as in Proposition 5.2. Since we have the trivial upper bound of 1 on
$g$ be as in Proposition 5.2. Since we have the trivial upper bound of 1 on ![]() $| \Phi _\pi '(h)|$ for all
$| \Phi _\pi '(h)|$ for all ![]() $h$, and since
$h$, and since ![]() $g \in K^\ast (1)$, we may assume that
$g \in K^\ast (1)$, we may assume that ![]() $1\leqslant j< n_0 -1$. Furthermore, by decreasing
$1\leqslant j< n_0 -1$. Furthermore, by decreasing ![]() $j$ if necessary, we may assume that
$j$ if necessary, we may assume that ![]() $g \in K^\ast (j)$. So, putting
$g \in K^\ast (j)$. So, putting ![]() $g = \big (\begin {smallmatrix}{a} & {b}\\ {c} & {d}\end {smallmatrix}\big )$, we have
$g = \big (\begin {smallmatrix}{a} & {b}\\ {c} & {d}\end {smallmatrix}\big )$, we have ![]() $\min (v(b),v(c)) = j$. Note that
$\min (v(b),v(c)) = j$. Note that ![]() $\Phi _\pi '(g) = \Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big )$, where
$\Phi _\pi '(g) = \Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big )$, where ![]() $c' = c\varpi ^{n_1}$,
$c' = c\varpi ^{n_1}$, ![]() $b' = b \varpi ^{-n_1}$. We consider two cases.
$b' = b \varpi ^{-n_1}$. We consider two cases.
Case I: ![]() $v(c) = j$. In this case we have
$v(c) = j$. In this case we have ![]() $v(c') = n_1 + j$. Since
$v(c') = n_1 + j$. Since ![]() $v(d)=0$, a direct calculation shows that
$v(d)=0$, a direct calculation shows that
Therefore, (30) tells us that ![]() $\big |\Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big )\big | \ll q^{({j+n_1 - n})/{2} + O(1)} \ll q^{({j- n_1})/{2}+ O(1)}$, as required.
$\big |\Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big )\big | \ll q^{({j+n_1 - n})/{2} + O(1)} \ll q^{({j- n_1})/{2}+ O(1)}$, as required.
Case II: ![]() $v(c) > j$. In this case we have
$v(c) > j$. In this case we have ![]() $v(b)=j$. As before, we have
$v(b)=j$. As before, we have ![]() $v(b') = j-n_1$,
$v(b') = j-n_1$, ![]() $v(c') = v(c)+n_1$, and
$v(c') = v(c)+n_1$, and ![]() $\Phi _\pi '(g) = \Phi _\pi \big(\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big)$. We can see from a direct calculation that
$\Phi _\pi '(g) = \Phi _\pi \big(\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big)$. We can see from a direct calculation that
for some ![]() $m \in F$,
$m \in F$, ![]() $y \in {\mathfrak o}^\times$,
$y \in {\mathfrak o}^\times$, ![]() $z \in {\mathfrak o}^\times$, and
$z \in {\mathfrak o}^\times$, and ![]() $r = \min (n, v(c)+n_1)$. Note that
$r = \min (n, v(c)+n_1)$. Note that ![]() $v(b')\geqslant v(m)$.
$v(b')\geqslant v(m)$.
We claim that ![]() $\Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big ) =0$. Suppose not. Suppose first that
$\Phi _\pi \big (\big (\begin {smallmatrix}{a} & {b'}\\ {c'} & {d}\end {smallmatrix}\big )\big ) =0$. Suppose not. Suppose first that ![]() $v(c) < n_0-1$. Then
$v(c) < n_0-1$. Then ![]() $r=v(c)+n_1$ and using (31) we see that
$r=v(c)+n_1$ and using (31) we see that ![]() $v(m)= v(c)-n_0$. This gives us
$v(m)= v(c)-n_0$. This gives us ![]() $j-n_1=v(b')\geqslant v(m) =v(c)-n_0$ and hence that
$j-n_1=v(b')\geqslant v(m) =v(c)-n_0$ and hence that ![]() $v(c)\leqslant j$, which is a contradiction. Next, suppose that
$v(c)\leqslant j$, which is a contradiction. Next, suppose that ![]() $v(c)\geqslant n_0-1$. Then
$v(c)\geqslant n_0-1$. Then ![]() $n \geqslant r\geqslant n-1$ and using (32) we see that
$n \geqslant r\geqslant n-1$ and using (32) we see that ![]() $j-n_1=v(b')\geqslant v(m) \geqslant -1$. So,
$j-n_1=v(b')\geqslant v(m) \geqslant -1$. So, ![]() $j \geqslant n_1 -1$, which contradicts our earlier assumption that
$j \geqslant n_1 -1$, which contradicts our earlier assumption that ![]() $j < n_0-1$.
$j < n_0-1$.
5.5 The proof of Theorem 5.4
The assertions (31) and (32) of Theorem 5.4 have already been proven in [Reference HuHu18, Proposition 3.1]. So, we only need to prove the upper bound part in Theorem 5.4, i.e. (30).
For simplicity, denote
For the rest of this section, we fix an additive character ![]() $\psi$ of
$\psi$ of ![]() $F$ such that
$F$ such that ![]() $a(\psi )=0$ and consider the Whittaker model of
$a(\psi )=0$ and consider the Whittaker model of ![]() $\pi$ with respect to this character. Using the usual inner product in the Whittaker model, it follows that
$\pi$ with respect to this character. Using the usual inner product in the Whittaker model, it follows that
where ![]() $W^{(i)}( x )=W_{\pi }\big (\big (\begin {smallmatrix}{ x } & {0}\\ {0} & {1}\end {smallmatrix}\big ) \big (\begin {smallmatrix}{1} & {0}\\ {\varpi ^i} & {1}\end {smallmatrix}\big )\big )$ and
$W^{(i)}( x )=W_{\pi }\big (\big (\begin {smallmatrix}{ x } & {0}\\ {0} & {1}\end {smallmatrix}\big ) \big (\begin {smallmatrix}{1} & {0}\\ {\varpi ^i} & {1}\end {smallmatrix}\big )\big )$ and ![]() $W_\pi$ is the local Whittaker newform (see, e.g., § 3 of [Reference HuHu18] for more details).
$W_\pi$ is the local Whittaker newform (see, e.g., § 3 of [Reference HuHu18] for more details).
The basic tool to analyse such integrals is the ![]() $p$-adic stationary phase analysis. Roughly speaking, we will rewrite this integral and break it up into pieces, and we will prove (using orthogonality of characters) that most of these pieces vanish. The required bounds will follow by counting the number of non-vanishing pieces. Since
$p$-adic stationary phase analysis. Roughly speaking, we will rewrite this integral and break it up into pieces, and we will prove (using orthogonality of characters) that most of these pieces vanish. The required bounds will follow by counting the number of non-vanishing pieces. Since ![]() $n >2$ and
$n >2$ and ![]() $q$ is odd, there are two possibilities for
$q$ is odd, there are two possibilities for ![]() $\pi$: principal series representations and dihedral supercuspidal representations. We deal with each below.
$\pi$: principal series representations and dihedral supercuspidal representations. We deal with each below.
5.5.1 Principal series representation
Let ![]() $\pi =\pi (\mu _1,\mu _2)$ be a principal series representation. In this case
$\pi =\pi (\mu _1,\mu _2)$ be a principal series representation. In this case ![]() $n$ is even and we take
$n$ is even and we take ![]() $\mu _2 = \mu _1^{-1} = \mu$,
$\mu _2 = \mu _1^{-1} = \mu$, ![]() $a(\mu )=n_1=n_0=n/2$. Denote
$a(\mu )=n_1=n_0=n/2$. Denote
Using the usual interpretation as a Gauss sum (see, e.g., [Reference SahaSah16, (6)]), we see that ![]() $|C_0|\asymp {1}/{q^{n_0/2}}$.
$|C_0|\asymp {1}/{q^{n_0/2}}$.
By [Reference HuHu17, Lemma 2.12], we have the following lemma.
Lemma 5.5 When ![]() $n_0 < i\leqslant n$,
$n_0 < i\leqslant n$, ![]() $W^{(i)}(x)$ is supported on
$W^{(i)}(x)$ is supported on ![]() $x \in {\mathfrak o}^\times$ and for
$x \in {\mathfrak o}^\times$ and for ![]() $x \in {\mathfrak o}^\times$ we have
$x \in {\mathfrak o}^\times$ we have
Note that the condition ![]() $a(\pi )\geqslant 3$ implies that
$a(\pi )\geqslant 3$ implies that ![]() $a(\mu )\geqslant 2$. Let
$a(\mu )\geqslant 2$. Let ![]() ${\alpha }$ be the constant associated to
${\alpha }$ be the constant associated to ![]() $\mu$ by Lemma 5.1. Then
$\mu$ by Lemma 5.1. Then ![]() $v({\alpha })=-n_0$.
$v({\alpha })=-n_0$.
By the results of [Reference HuHu18], ![]() $\Phi _\pi ^{(i)}(a,m)$ is supported on
$\Phi _\pi ^{(i)}(a,m)$ is supported on ![]() $v(a)=0$ and
$v(a)=0$ and ![]() $v(m)=i-n>-n_0$. Then, by (34),
$v(m)=i-n>-n_0$. Then, by (34),
 \begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\int_{v(x)=0}\psi(mx)\int_{u\in {\mathfrak o}^\times} \mu(1+u\varpi^{i-n_0})\mu(a x u)\psi(-\varpi^{-n_0}a x u)\,du\,d^\times x \nonumber\\ &=C_0^{-1}\iint_{v(x)=v(u)=0} \psi(mxu)\mu(1+u^{-1}\varpi^{i-n_0})\mu(a x )\psi(-\varpi^{-n_0}a x )\,du\,d^\times x. \end{align}
\begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\int_{v(x)=0}\psi(mx)\int_{u\in {\mathfrak o}^\times} \mu(1+u\varpi^{i-n_0})\mu(a x u)\psi(-\varpi^{-n_0}a x u)\,du\,d^\times x \nonumber\\ &=C_0^{-1}\iint_{v(x)=v(u)=0} \psi(mxu)\mu(1+u^{-1}\varpi^{i-n_0})\mu(a x )\psi(-\varpi^{-n_0}a x )\,du\,d^\times x. \end{align} The idea is to break the above integral into small intervals, on each of which we can apply Lemma 5.1 to analyse the integral and get easy vanishing for most of the small intervals. This is the exact analogue of the archimedean stationary phase analysis. In the integrand in (37), write ![]() $u=u_0(1+{{\Delta }} u)$ for
$u=u_0(1+{{\Delta }} u)$ for ![]() $u_0\in {\mathfrak o}^\times / (1+\mathfrak p^{\lceil (n-i)/2\rceil })$ and
$u_0\in {\mathfrak o}^\times / (1+\mathfrak p^{\lceil (n-i)/2\rceil })$ and ![]() ${{\Delta }} u\in \mathfrak p^{\lceil (n-i)/2\rceil }$, and
${{\Delta }} u\in \mathfrak p^{\lceil (n-i)/2\rceil }$, and ![]() $x=x_0(1+{{\Delta }} x)$ for
$x=x_0(1+{{\Delta }} x)$ for ![]() $x_0\in {\mathfrak o}^\times /(1+\mathfrak p^{\lceil n_0/2\rceil })$ and
$x_0\in {\mathfrak o}^\times /(1+\mathfrak p^{\lceil n_0/2\rceil })$ and ![]() ${{\Delta }} x\in \mathfrak p^{\lceil n_0/2\rceil }$. Using Lemma 5.1 and the invariance properties of
${{\Delta }} x\in \mathfrak p^{\lceil n_0/2\rceil }$. Using Lemma 5.1 and the invariance properties of ![]() $\psi$ and
$\psi$ and ![]() $\mu$, we get
$\mu$, we get
 \begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\sum_{x_0,u_0} \psi(mx_0u_0)\mu(1+u_0^{-1}\varpi^{i-n_0})\mu(a x_0 )\psi(-\varpi^{-n_0}a x_0 ) \nonumber\\ & \quad \times \int_{\mathfrak p^{\lceil ({n-i})/2\rceil} } \int_{\mathfrak p^{\lceil ({n_0})/2\rceil} } \psi\Big(\vphantom{\frac{\varpi^{i-n_0}u_0^{-1}}{1+\varpi^{i-n_0}u_0^{-1}}}mu_0x_0{{\Delta}} x+mx_0u_0{{\Delta}} u\nonumber\\ &\quad -{\alpha}\frac{\varpi^{i-n_0}u_0^{-1}}{1+\varpi^{i-n_0}u_0^{-1}} {{\Delta}} u+{\alpha} {{\Delta}} x-\varpi^{-n_0}ax_0{{\Delta}} x\Big) d{{\Delta}} x \,d{{\Delta}} u. \end{align}
\begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\sum_{x_0,u_0} \psi(mx_0u_0)\mu(1+u_0^{-1}\varpi^{i-n_0})\mu(a x_0 )\psi(-\varpi^{-n_0}a x_0 ) \nonumber\\ & \quad \times \int_{\mathfrak p^{\lceil ({n-i})/2\rceil} } \int_{\mathfrak p^{\lceil ({n_0})/2\rceil} } \psi\Big(\vphantom{\frac{\varpi^{i-n_0}u_0^{-1}}{1+\varpi^{i-n_0}u_0^{-1}}}mu_0x_0{{\Delta}} x+mx_0u_0{{\Delta}} u\nonumber\\ &\quad -{\alpha}\frac{\varpi^{i-n_0}u_0^{-1}}{1+\varpi^{i-n_0}u_0^{-1}} {{\Delta}} u+{\alpha} {{\Delta}} x-\varpi^{-n_0}ax_0{{\Delta}} x\Big) d{{\Delta}} x \,d{{\Delta}} u. \end{align}
For the innermost integral involving ![]() ${{\Delta }} x$,
${{\Delta }} x$, ![]() ${{\Delta }} u$ to be non-zero, we must have that
${{\Delta }} u$ to be non-zero, we must have that
From the first equation, we get that
So, there is a unique ![]() $x_0 \mod \varpi ^{\lfloor {n_0}/{2}\rfloor }$ for each
$x_0 \mod \varpi ^{\lfloor {n_0}/{2}\rfloor }$ for each ![]() $u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$ satisfying the above. As a trivial consequence, there are at most
$u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$ satisfying the above. As a trivial consequence, there are at most ![]() $q$ solutions of
$q$ solutions of ![]() $x_0\mod \varpi ^{\lceil {n_0}/{2}\rceil }$ for each
$x_0\mod \varpi ^{\lceil {n_0}/{2}\rceil }$ for each ![]() $u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$.
$u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$.
Next, by computing (39)![]() $\,\times\, mu_0$ – (40)
$\,\times\, mu_0$ – (40)![]() $\,\times\, (mu_0-\varpi ^{-n_0}a)$, we get the following necessary condition for non-vanishing:
$\,\times\, (mu_0-\varpi ^{-n_0}a)$, we get the following necessary condition for non-vanishing:
Here we have used that ![]() $-\lceil {n_0}/{2}\rceil +i-n\geqslant -\lceil ({n-i})/{2}\rceil -n_0$. This congruence is equivalent to
$-\lceil {n_0}/{2}\rceil +i-n\geqslant -\lceil ({n-i})/{2}\rceil -n_0$. This congruence is equivalent to
as ![]() $v({\alpha })=-n_0$. Note that
$v({\alpha })=-n_0$. Note that ![]() $v(mu_0^2)=v(\varpi ^{i-n}a)=i-n < v(2\varpi ^{i-n_0}m u_0)$. So, this quadratic equation is not degenerate when
$v(mu_0^2)=v(\varpi ^{i-n}a)=i-n < v(2\varpi ^{i-n_0}m u_0)$. So, this quadratic equation is not degenerate when ![]() $p\neq 2$, and we can solve for at most two solutions of
$p\neq 2$, and we can solve for at most two solutions of ![]() $u_0\mod \varpi ^{\lfloor ({n-i})/{2}\rfloor }$ and consequently at most
$u_0\mod \varpi ^{\lfloor ({n-i})/{2}\rfloor }$ and consequently at most ![]() $2q$ solutions of
$2q$ solutions of ![]() $u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$.
$u_0\mod \varpi ^{\lceil ({n-i})/{2}\rceil }$.
In summary, we have that there are ![]() $\leqslant 2q^2$ pairs
$\leqslant 2q^2$ pairs ![]() $(x_0, u_0)$ contributing to (38) and so we get
$(x_0, u_0)$ contributing to (38) and so we get
as required.
Remark 5.6 By going through the proof above more carefully (and looking at the cases ![]() $n_0$ odd and
$n_0$ odd and ![]() $n_0$ even) the implied constant in
$n_0$ even) the implied constant in ![]() $O(1)$ in (30) can be worked out more explicitly. In particular, when there are
$O(1)$ in (30) can be worked out more explicitly. In particular, when there are ![]() $O(q)$ solutions of
$O(q)$ solutions of ![]() $x_0$ and/or
$x_0$ and/or ![]() $u_0$, the sums in
$u_0$, the sums in ![]() $x_0,u_0$ can be reduced to sums over the residue field and we expect complete square-root cancellation. The same comment applies to the supercuspidal representation case below.
$x_0,u_0$ can be reduced to sums over the residue field and we expect complete square-root cancellation. The same comment applies to the supercuspidal representation case below.
5.5.2 Supercuspidal representations
When ![]() $2\nmid q$,
$2\nmid q$, ![]() $\pi$ is associated by compact induction theory to a character
$\pi$ is associated by compact induction theory to a character ![]() $\theta$ over a quadratic field extension
$\theta$ over a quadratic field extension ![]() ${E}/{F}$ with ramification index
${E}/{F}$ with ramification index ![]() $e_{E}$. Their relations are given explicitly as follows (see [Reference Bushnell and HenniartBH06]).
$e_{E}$. Their relations are given explicitly as follows (see [Reference Bushnell and HenniartBH06]).
(i)
 $a(\pi )=n=2n_0$ corresponds to
$a(\pi )=n=2n_0$ corresponds to  $e_{E}=1$ and
$e_{E}=1$ and  $a(\theta )=n_0$.
$a(\theta )=n_0$.(ii)
 $n=2n_0+1$ corresponds to
$n=2n_0+1$ corresponds to  $e_{E}=2$ and
$e_{E}=2$ and  $a(\theta )=2n_0$.
$a(\theta )=2n_0$.
In the following we shall give uniform formulations and estimates for both of these cases, which one can verify case by case according to this classification. For simplicity, let ![]() ${E}={F}(\sqrt {D})$ with
${E}={F}(\sqrt {D})$ with ![]() $v_{F}(D)=e_{E}-1$. We let
$v_{F}(D)=e_{E}-1$. We let ![]() ${\mathfrak o}_E$ denote the ring of integers of
${\mathfrak o}_E$ denote the ring of integers of ![]() $E$,
$E$, ![]() $\varpi _E$ denote a uniformizer of
$\varpi _E$ denote a uniformizer of ![]() $E$, and
$E$, and ![]() $\mathfrak p_E = \varpi _E{\mathfrak o}_E$. Let
$\mathfrak p_E = \varpi _E{\mathfrak o}_E$. Let ![]() $\psi _{E}=\psi \circ \textrm {tr}_{{E}/{F}}$. It is easy to check that
$\psi _{E}=\psi \circ \textrm {tr}_{{E}/{F}}$. It is easy to check that ![]() $a(\psi _{E})=-e_{E}+1$ since
$a(\psi _{E})=-e_{E}+1$ since ![]() $a(\psi )=0$. Let
$a(\psi )=0$. Let
Again, by the usual interpretation as a Gauss sum, we get ![]() $|C_0|\asymp {1}/{q^{a(\pi )/2}}$. Checking case by case, one can also see that for
$|C_0|\asymp {1}/{q^{a(\pi )/2}}$. Checking case by case, one can also see that for ![]() $u$ in the domain of the integral,
$u$ in the domain of the integral,
The following lemma is a reformulation of [Reference AssingAss19, Lemma 3.1].
Lemma 5.7 When ![]() $i>n_0$,
$i>n_0$, ![]() $W^{(i)}(x)$ is supported on
$W^{(i)}(x)$ is supported on ![]() $v(x)=0$ and, on the support,
$v(x)=0$ and, on the support,
Again by [Reference HuHu18] the matrix coefficient ![]() $\Phi _\pi ^{(i)}(a,m)$ is supported on
$\Phi _\pi ^{(i)}(a,m)$ is supported on ![]() $v(a)=0$,
$v(a)=0$, ![]() $v(m)=i-n$ when
$v(m)=i-n$ when ![]() $n_0 < i < n-1$. On the support, by the above lemma and (34),
$n_0 < i < n-1$. On the support, by the above lemma and (34),
 \begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\int_{v(x)=0}\psi(mx)\int_{v_{E}(u)=-a(\theta)-e_{E}+1}\theta^{-1}(u) \psi \biggl(-\frac{1}{ax}\varpi^{i}N_{{E}/{F}}(u)\biggr)\psi_{E}(u)\,d^\times u\,d^\times x\nonumber\\ &=C_0^{-1}\int_{v(x)=0}\psi \biggl(m\frac{1}{x}\biggr)\int_{v_{E}(u)=-a(\theta)-e_{E}+1}\theta^{-1}(u) \psi \biggl(-\frac{x}{a}\varpi^{i}N_{{E}/{F}}(u)\biggr)\psi_{E}(u)\,d^\times u\,d^\times x. \end{align}
\begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\int_{v(x)=0}\psi(mx)\int_{v_{E}(u)=-a(\theta)-e_{E}+1}\theta^{-1}(u) \psi \biggl(-\frac{1}{ax}\varpi^{i}N_{{E}/{F}}(u)\biggr)\psi_{E}(u)\,d^\times u\,d^\times x\nonumber\\ &=C_0^{-1}\int_{v(x)=0}\psi \biggl(m\frac{1}{x}\biggr)\int_{v_{E}(u)=-a(\theta)-e_{E}+1}\theta^{-1}(u) \psi \biggl(-\frac{x}{a}\varpi^{i}N_{{E}/{F}}(u)\biggr)\psi_{E}(u)\,d^\times u\,d^\times x. \end{align} Since ![]() $a(\pi )\geqslant 3$, we have
$a(\pi )\geqslant 3$, we have ![]() $a(\theta )\geqslant 2$. Let
$a(\theta )\geqslant 2$. Let ![]() ${\alpha }\in {E}^\times$ be the constant associated to
${\alpha }\in {E}^\times$ be the constant associated to ![]() $\theta$ by Lemma 5.1; then
$\theta$ by Lemma 5.1; then ![]() $v_{E}({\alpha })=-a(\theta )+a(\psi _{E})=-a(\theta )-e_{E}+1$. As
$v_{E}({\alpha })=-a(\theta )+a(\psi _{E})=-a(\theta )-e_{E}+1$. As ![]() $\theta |_{{F}^\times }$ is essentially the central character
$\theta |_{{F}^\times }$ is essentially the central character ![]() $w_\pi$, which is trivial, we can assume that
$w_\pi$, which is trivial, we can assume that ![]() ${\alpha }$ is purely imaginary in
${\alpha }$ is purely imaginary in ![]() ${E}^\times$. In the integrand in (48), write
${E}^\times$. In the integrand in (48), write ![]() $x=x_0(1+{{\Delta }} x)$ with
$x=x_0(1+{{\Delta }} x)$ with ![]() $x_0\in {\mathfrak o}^\times /(1+\mathfrak p^{\lceil (n-i)/2\rceil })$,
$x_0\in {\mathfrak o}^\times /(1+\mathfrak p^{\lceil (n-i)/2\rceil })$, ![]() ${{\Delta }} x\in \mathfrak p^{\lceil (n-i)/2\rceil }$, and
${{\Delta }} x\in \mathfrak p^{\lceil (n-i)/2\rceil }$, and
for ![]() $u_0\in (\varpi _E^{-a(\theta )-e_{E}+1}{\mathfrak o}_E/\varpi _E^{-\lfloor a(\theta )/2\rfloor -e_{E}+1}{\mathfrak o}_E)^\times$,
$u_0\in (\varpi _E^{-a(\theta )-e_{E}+1}{\mathfrak o}_E/\varpi _E^{-\lfloor a(\theta )/2\rfloor -e_{E}+1}{\mathfrak o}_E)^\times$, ![]() ${{\Delta }} u = {{\Delta }} a+\sqrt {D}{{\Delta }} b\in \varpi _{E}^{\lceil a(\theta )/2\rceil } {\mathfrak o}_{E}$.
${{\Delta }} u = {{\Delta }} a+\sqrt {D}{{\Delta }} b\in \varpi _{E}^{\lceil a(\theta )/2\rceil } {\mathfrak o}_{E}$.
Then
 \begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\sum_{x_0,u_0}\psi \bigg(\frac{m}{x_0}\bigg)\theta^{-1}(u_0)\psi \biggl(-\frac{x_0}{a}\varpi^i N_{{E}/{F}}(u_0)\biggr)\psi_{E}(u_0) \nonumber\\ &\quad \times \iint_{\substack{{{\Delta}} x \in \mathfrak p^{\lceil ({n-i})/2\rceil} \\ {{\Delta}} u \in \mathfrak p_{E}^{\lceil {a(\theta)}/2\rceil} }}F_{x_0, u_0}({{\Delta}} x, {{\Delta}} u) \, d{{\Delta}} x \,d{{\Delta}} u, \end{align}
\begin{align} \Phi_\pi^{(i)}(a,m)&=C_0^{-1}\sum_{x_0,u_0}\psi \bigg(\frac{m}{x_0}\bigg)\theta^{-1}(u_0)\psi \biggl(-\frac{x_0}{a}\varpi^i N_{{E}/{F}}(u_0)\biggr)\psi_{E}(u_0) \nonumber\\ &\quad \times \iint_{\substack{{{\Delta}} x \in \mathfrak p^{\lceil ({n-i})/2\rceil} \\ {{\Delta}} u \in \mathfrak p_{E}^{\lceil {a(\theta)}/2\rceil} }}F_{x_0, u_0}({{\Delta}} x, {{\Delta}} u) \, d{{\Delta}} x \,d{{\Delta}} u, \end{align}
where ![]() $F_{x_0, u_0}({{\Delta }} x, {{\Delta }} u)= \psi (-({m}/{x_0}){{\Delta }} x-2{\alpha } \sqrt {D}{{\Delta }} b-({x_0}/{a})\varpi ^i N_{{E}/F}(u_0)({{\Delta }} x - 2 {{\Delta }} a)+2a_0{{\Delta }} a+2Db_0{{\Delta }} b )$ for
$F_{x_0, u_0}({{\Delta }} x, {{\Delta }} u)= \psi (-({m}/{x_0}){{\Delta }} x-2{\alpha } \sqrt {D}{{\Delta }} b-({x_0}/{a})\varpi ^i N_{{E}/F}(u_0)({{\Delta }} x - 2 {{\Delta }} a)+2a_0{{\Delta }} a+2Db_0{{\Delta }} b )$ for ![]() ${{\Delta }} u= {{\Delta }} a+\sqrt {D}{{\Delta }} b$ with
${{\Delta }} u= {{\Delta }} a+\sqrt {D}{{\Delta }} b$ with ![]() ${{\Delta }} a$,
${{\Delta }} a$, ![]() ${{\Delta }} b$ in
${{\Delta }} b$ in ![]() ${\mathfrak o}$. Here we have used that
${\mathfrak o}$. Here we have used that
 \begin{gather*} \theta^{-1}(1+{{\Delta}} u)=\psi_E(-\alpha {{\Delta}} u)=\psi_E(-\alpha {{\Delta}} a-\alpha\sqrt{D}{{\Delta}} b)=\psi(-2\alpha\sqrt{D}{{\Delta}} b),\\ \psi_E(u_0{{\Delta}} u)=\psi(2a_0{{\Delta}} a+2Db_0{{\Delta}} b). \end{gather*}
\begin{gather*} \theta^{-1}(1+{{\Delta}} u)=\psi_E(-\alpha {{\Delta}} u)=\psi_E(-\alpha {{\Delta}} a-\alpha\sqrt{D}{{\Delta}} b)=\psi(-2\alpha\sqrt{D}{{\Delta}} b),\\ \psi_E(u_0{{\Delta}} u)=\psi(2a_0{{\Delta}} a+2Db_0{{\Delta}} b). \end{gather*} Using the fact that ![]() $a(\psi )=0$, we observe that in order for the integral in (49) to be non-zero, we need the following conditions to hold: For all
$a(\psi )=0$, we observe that in order for the integral in (49) to be non-zero, we need the following conditions to hold: For all ![]() $x_1$,
$x_1$, ![]() $a_1$,
$a_1$, ![]() $b_1$ in
$b_1$ in ![]() ${\mathfrak o}$ such that
${\mathfrak o}$ such that ![]() $x_1 \in \mathfrak p^{\lceil ({n-i})/2\rceil }$,
$x_1 \in \mathfrak p^{\lceil ({n-i})/2\rceil }$, ![]() $a_1+\sqrt {D}b_1 \in \mathfrak p_{E}^{\lceil {a(\theta )}/2\rceil }$, we have
$a_1+\sqrt {D}b_1 \in \mathfrak p_{E}^{\lceil {a(\theta )}/2\rceil }$, we have
Now, using a very similar analysis as in the principal series case, we shall see that the number of pairs ![]() $(x_0, u_0)$ satisfying (50), (51), and (52) is
$(x_0, u_0)$ satisfying (50), (51), and (52) is ![]() $\ll q^{O(1)}.$
$\ll q^{O(1)}.$
Consider the number of ![]() $b_0$ satisfying (52) first. When
$b_0$ satisfying (52) first. When ![]() $e_E=1$, or
$e_E=1$, or ![]() $e_{E}=2$ and
$e_{E}=2$ and ![]() $a(\theta )/2$ is odd, we can choose
$a(\theta )/2$ is odd, we can choose ![]() $a_1$,
$a_1$, ![]() $b_1$ in
$b_1$ in ![]() ${\mathfrak o}$ such that
${\mathfrak o}$ such that ![]() $a_1+\sqrt {D}b_1\in \mathfrak p_{E}^{\lceil a(\theta )/2\rceil }$,
$a_1+\sqrt {D}b_1\in \mathfrak p_{E}^{\lceil a(\theta )/2\rceil }$, ![]() $b_1 \in \varpi _{E}^{\lceil a(\theta )/2\rceil -e_E+1}{\mathfrak o}_{E}^\times \cap {\mathfrak o}$, which combined with (52) gives us
$b_1 \in \varpi _{E}^{\lceil a(\theta )/2\rceil -e_E+1}{\mathfrak o}_{E}^\times \cap {\mathfrak o}$, which combined with (52) gives us
while by the definition of ![]() $u_0$,
$u_0$, ![]() $b_0\sqrt {D}$ is well defined up to
$b_0\sqrt {D}$ is well defined up to ![]() $\mathfrak p_{E}^{-\lfloor a(\theta )/2\rfloor -e_E+1}$. Thus,
$\mathfrak p_{E}^{-\lfloor a(\theta )/2\rfloor -e_E+1}$. Thus,
When ![]() $e_{E}=2$ and
$e_{E}=2$ and ![]() $a(\theta )/2$ is even, we can choose
$a(\theta )/2$ is even, we can choose ![]() $b_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil }{\mathfrak o}_E^\times \cap {\mathfrak o}$ and this time (52) gives us
$b_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil }{\mathfrak o}_E^\times \cap {\mathfrak o}$ and this time (52) gives us ![]() $b_0\equiv ({\alpha }/{\sqrt {D}}) \mod \mathfrak p_{E}^{-\lceil a(\theta )/2\rceil -2e_E+2}$. By the same argument as above, (54) still holds in this case.
$b_0\equiv ({\alpha }/{\sqrt {D}}) \mod \mathfrak p_{E}^{-\lceil a(\theta )/2\rceil -2e_E+2}$. By the same argument as above, (54) still holds in this case.
Similarly, for each fixed ![]() $u_0$, there exist solutions for
$u_0$, there exist solutions for ![]() $x_0$ from (50) if and only if
$x_0$ from (50) if and only if
is a square modulo ![]() $\varpi ^{\lfloor (n-i)/2\rfloor }$. In that case we obtain
$\varpi ^{\lfloor (n-i)/2\rfloor }$. In that case we obtain
Here we have used that ![]() $p\neq 2$. So, by the definition of
$p\neq 2$. So, by the definition of ![]() $x_0$,
$x_0$,
Finally, we come to counting ![]() $a_0$. When
$a_0$. When ![]() $e_{E}=1$, or
$e_{E}=1$, or ![]() $e_{E}=2$ and
$e_{E}=2$ and ![]() $a(\theta )/2$ is even, we can choose
$a(\theta )/2$ is even, we can choose ![]() $a_1$,
$a_1$, ![]() $b_1$ so that
$b_1$ so that ![]() $a_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil }{\mathfrak o}_{E}^\times \cap {\mathfrak o}$,
$a_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil }{\mathfrak o}_{E}^\times \cap {\mathfrak o}$, ![]() $a_1+\sqrt {D} b_1\in \mathfrak p_{E}^{\lceil a(\theta )/2\rceil }$, so that from (51) we now deduce that
$a_1+\sqrt {D} b_1\in \mathfrak p_{E}^{\lceil a(\theta )/2\rceil }$, so that from (51) we now deduce that
Note that if ![]() $v_E(({x_0}/{a})\varpi ^iN_{E/F}(u_0))=e_E(i-n)\geqslant -\lceil a(\theta )/2\rceil$, we get a unique solution
$v_E(({x_0}/{a})\varpi ^iN_{E/F}(u_0))=e_E(i-n)\geqslant -\lceil a(\theta )/2\rceil$, we get a unique solution ![]() $a_0\equiv 0\mod \varpi _E^{-\lceil a(\theta )/2\rceil }$ and by the definition of
$a_0\equiv 0\mod \varpi _E^{-\lceil a(\theta )/2\rceil }$ and by the definition of ![]() $a_0$ and the previous results,
$a_0$ and the previous results,
Otherwise when ![]() $e_E(i-n) < -\lceil a(\theta )/2\rceil$, (57) is a non-trivial congruence relation and
$e_E(i-n) < -\lceil a(\theta )/2\rceil$, (57) is a non-trivial congruence relation and ![]() $v(a_0)=i-n$. As
$v(a_0)=i-n$. As ![]() $p\neq 2$, we have for any solution
$p\neq 2$, we have for any solution ![]() $a_0$,
$a_0$,
Multiplying it with (57) and substituting (55), we get
One can get at most two solutions of ![]() $a_0\mod \varpi _E^{-\lceil a(\theta )/2\rceil }$ for each fixed
$a_0\mod \varpi _E^{-\lceil a(\theta )/2\rceil }$ for each fixed ![]() $b_0$. So, (58) is still true.
$b_0$. So, (58) is still true.
If ![]() $e_{E}=2$ and
$e_{E}=2$ and ![]() $a(\theta )/2$ is odd, we can instead choose
$a(\theta )/2$ is odd, we can instead choose ![]() $a_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil +1}{\mathfrak o}^\times _{E} \cap {\mathfrak o}$ in the argument above (57). The rest of the discussions are similar and (58) still holds.
$a_1\in \varpi _{E}^{\lceil a(\theta )/2\rceil +1}{\mathfrak o}^\times _{E} \cap {\mathfrak o}$ in the argument above (57). The rest of the discussions are similar and (58) still holds.
In conclusion, we get that
as required.
6. An application to subconvexity
In this section, we explain how Corollary 4.9 leads to a subconvexity result for certain central ![]() $L$-values.
$L$-values.
6.1 The setup and the main result
Throughout this section, we will go back to the global setting and freely use the notation defined in §§ 2.1 and 4.1. Recall that we have fixed an indefinite quaternion division algebra ![]() $D$ over
$D$ over ![]() ${\mathbb {Q}}$ of discriminant
${\mathbb {Q}}$ of discriminant ![]() $d$. In addition, for this section, we fix:
$d$. In addition, for this section, we fix:
– a squarefree integer
 $P$ such that
$P$ such that  $(P, 2d)=1$;
$(P, 2d)=1$;– a quadratic number field
 $K/{\mathbb {Q}}$ such that:
$K/{\mathbb {Q}}$ such that:
* all primes dividing
 $P$ are split in
$P$ are split in  $K$;
$K$;* all primes dividing
 $d$ are inert in
$d$ are inert in  $K$.
$K$.
Let ![]() $\mathcal {S}_{P}$ denote the set of irreducible, unitary, cuspidal, automorphic representations
$\mathcal {S}_{P}$ denote the set of irreducible, unitary, cuspidal, automorphic representations ![]() $\pi = \otimes _v \pi _v$ of
$\pi = \otimes _v \pi _v$ of ![]() $G({\mathbb {A}})$ with the following properties:
$G({\mathbb {A}})$ with the following properties:
(i)
 $\pi$ has trivial central character;
$\pi$ has trivial central character;(ii) if
 $\ell$ is a prime such that
$\ell$ is a prime such that  $\ell \nmid P$, then
$\ell \nmid P$, then  $\pi _\ell$ is spherical (i.e. has a non-zero
$\pi _\ell$ is spherical (i.e. has a non-zero  $K_\ell$-fixed vector).
$K_\ell$-fixed vector).
Note that (using the notation of § 4.1), for any ![]() $\pi \in \mathcal {S}_{P}$, we have
$\pi \in \mathcal {S}_{P}$, we have ![]() $C'(\pi )$ divides
$C'(\pi )$ divides ![]() $P$ and hence
$P$ and hence ![]() $C(\pi )$ is divisible only by primes dividing
$C(\pi )$ is divisible only by primes dividing ![]() $P$. We remind the reader that
$P$. We remind the reader that ![]() $C(\pi )$ denotes the ‘away-from-
$C(\pi )$ denotes the ‘away-from-![]() $d$-part’ of the conductor of
$d$-part’ of the conductor of ![]() $\pi$ (the conductor of
$\pi$ (the conductor of ![]() $\pi$ equals
$\pi$ equals ![]() $dC(\pi )$). We let
$dC(\pi )$). We let ![]() ${\mathcal {O}}_K$ denote the ring of integers of
${\mathcal {O}}_K$ denote the ring of integers of ![]() $K$ and
$K$ and ![]() $\rho _K$ the quadratic character on
$\rho _K$ the quadratic character on ![]() ${\mathbb {Q}}^\times \backslash {\mathbb {A}}^\times$ associated to the extension
${\mathbb {Q}}^\times \backslash {\mathbb {A}}^\times$ associated to the extension ![]() $K/{\mathbb {Q}}$.
$K/{\mathbb {Q}}$.
Remark 6.1 By the Jacquet–Langlands correspondence, the set ![]() $\mathcal {S}_P$ is in functorial bijection with the set of irreducible, unitary, cuspidal, automorphic representations on
$\mathcal {S}_P$ is in functorial bijection with the set of irreducible, unitary, cuspidal, automorphic representations on ![]() $\rm {PGL_2}({\mathbb {A}})$ whose conductor equals
$\rm {PGL_2}({\mathbb {A}})$ whose conductor equals ![]() $dC$ for some
$dC$ for some ![]() $C|P^\infty$.
$C|P^\infty$.
Given ![]() $\pi \in \mathcal {S}_{P}$ and a character
$\pi \in \mathcal {S}_{P}$ and a character ![]() $\chi$ of
$\chi$ of ![]() $K^\times \backslash {\mathbb {A}}_K^\times$ such that
$K^\times \backslash {\mathbb {A}}_K^\times$ such that ![]() $\chi |_{{\mathbb {A}}^\times } = 1$, we are interested in the central
$\chi |_{{\mathbb {A}}^\times } = 1$, we are interested in the central ![]() $L$-value
$L$-value ![]() $L(1/2 , \pi \times {\mathcal {AI}}(\chi ))$ of the Rankin–Selberg
$L(1/2 , \pi \times {\mathcal {AI}}(\chi ))$ of the Rankin–Selberg ![]() $L$-function. Here
$L$-function. Here ![]() ${\mathcal {AI}}(\chi )$ denotes the global automorphic induction of
${\mathcal {AI}}(\chi )$ denotes the global automorphic induction of ![]() $\chi$ from
$\chi$ from ![]() ${\mathbb {A}}_K^\times$ to
${\mathbb {A}}_K^\times$ to ![]() $\textrm {GL}_2({\mathbb {A}})$, whose existence follows either from the converse theorem (see Chapter 7 of [Reference GelbartGel75]) or more explicitly via the theta correspondence [Reference Shalika and TanakaST69]. By purely local calculations [Reference RohrlichRoh94, (a2)], it can be seen that the conductor of
$\textrm {GL}_2({\mathbb {A}})$, whose existence follows either from the converse theorem (see Chapter 7 of [Reference GelbartGel75]) or more explicitly via the theta correspondence [Reference Shalika and TanakaST69]. By purely local calculations [Reference RohrlichRoh94, (a2)], it can be seen that the conductor of ![]() ${\mathcal {AI}}(\chi )$ equals
${\mathcal {AI}}(\chi )$ equals ![]() $\textrm {disc}(K) N(\textrm {cond}(\chi ))$.
$\textrm {disc}(K) N(\textrm {cond}(\chi ))$.
Theorem 6.2 Let ![]() $P$,
$P$, ![]() $K$, and
$K$, and ![]() $\mathcal {S}_P$ be as above. Let
$\mathcal {S}_P$ be as above. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $K^\times \backslash {\mathbb {A}}_K^\times$ such that
$K^\times \backslash {\mathbb {A}}_K^\times$ such that ![]() $\chi |_{{\mathbb {A}}^\times } = 1$ and such that
$\chi |_{{\mathbb {A}}^\times } = 1$ and such that ![]() $\gcd (C(\chi ), d)=1$, where
$\gcd (C(\chi ), d)=1$, where ![]() $C(\chi )= N(\textrm {cond}(\chi ))$ equals the absolute norm of the conductor of
$C(\chi )= N(\textrm {cond}(\chi ))$ equals the absolute norm of the conductor of ![]() $\chi$. Then, for any
$\chi$. Then, for any ![]() $\pi \in \mathcal {S}_P$, we have
$\pi \in \mathcal {S}_P$, we have
The above theorem immediately implies a subconvexity result for ![]() $L(1/2, \pi \times {\mathcal {AI}}(\chi ))$ for fixed
$L(1/2, \pi \times {\mathcal {AI}}(\chi ))$ for fixed ![]() $\chi$ and varying
$\chi$ and varying ![]() $\pi \in \mathcal {S}_P$.
$\pi \in \mathcal {S}_P$.
Corollary 6.3 Let ![]() $P$,
$P$, ![]() $K$,
$K$, ![]() $\chi$, and
$\chi$, and ![]() $\mathcal {S}_P$ be as in Theorem 6.2. Then, for
$\mathcal {S}_P$ be as in Theorem 6.2. Then, for ![]() $\pi \in \mathcal {S}_P$, we have
$\pi \in \mathcal {S}_P$, we have
where ![]() $C(\pi \times {\mathcal {AI}}(\chi ))$ denotes the (finite part of the) analytic conductor of
$C(\pi \times {\mathcal {AI}}(\chi ))$ denotes the (finite part of the) analytic conductor of ![]() $L(s, \pi \times {\mathcal {AI}}(\chi ))$.
$L(s, \pi \times {\mathcal {AI}}(\chi ))$.
Proof. Any ‘conductor dropping’ for ![]() $\pi \times {\mathcal {AI}}(\chi )$ is only potentially possible at primes
$\pi \times {\mathcal {AI}}(\chi )$ is only potentially possible at primes ![]() $p|P$ for which
$p|P$ for which ![]() $v_p(C(\chi )) = v_p(C(\pi ))>0$. More precisely, let
$v_p(C(\chi )) = v_p(C(\pi ))>0$. More precisely, let ![]() $\mathcal {P}_1$ be the set of prime numbers
$\mathcal {P}_1$ be the set of prime numbers ![]() $p$ such that
$p$ such that ![]() $p | C(\chi )$ and
$p | C(\chi )$ and ![]() $v_p(C(\chi )) = v_p(C(\pi ))$. Then, using Proposition 3.4 of [Reference TunnellTun78], we see that
$v_p(C(\chi )) = v_p(C(\pi ))$. Then, using Proposition 3.4 of [Reference TunnellTun78], we see that
where the ![]() $t_p$ are non-negative integers satisfying
$t_p$ are non-negative integers satisfying ![]() $t_p \leqslant 2v_p(C(\chi ))$. It follows immediately that
$t_p \leqslant 2v_p(C(\chi ))$. It follows immediately that
Remark 6.4 By definition, ![]() $L(s , \pi \times {\mathcal {AI}}(\chi ))$ is the finite part of the Langlands
$L(s , \pi \times {\mathcal {AI}}(\chi ))$ is the finite part of the Langlands ![]() $L$-function attached to the automorphic representation
$L$-function attached to the automorphic representation ![]() $\pi \boxtimes {\mathcal {AI}}(\chi )$ on
$\pi \boxtimes {\mathcal {AI}}(\chi )$ on ![]() $D^\times \times \textrm {GL}_2$. It is immediate that
$D^\times \times \textrm {GL}_2$. It is immediate that ![]() $L(s, \pi \times {\mathcal {AI}}(\chi )) = L(s, \pi ' \times {\mathcal {AI}}(\chi ))$, where
$L(s, \pi \times {\mathcal {AI}}(\chi )) = L(s, \pi ' \times {\mathcal {AI}}(\chi ))$, where ![]() $\pi '$ is the automorphic representation on
$\pi '$ is the automorphic representation on ![]() $\textrm {GL}_2({\mathbb {A}})$ associated to
$\textrm {GL}_2({\mathbb {A}})$ associated to ![]() $\pi$ via the Jacquet–Langlands correspondence. Hence,
$\pi$ via the Jacquet–Langlands correspondence. Hence, ![]() $L(s, \pi \times {\mathcal {AI}}(\chi ))$ can be viewed as an
$L(s, \pi \times {\mathcal {AI}}(\chi ))$ can be viewed as an ![]() $L$-function on
$L$-function on ![]() $\textrm {GL}_2({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$.
$\textrm {GL}_2({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$.
We remark that ![]() $G'=PD^\times$ is isomorphic to an orthogonal group
$G'=PD^\times$ is isomorphic to an orthogonal group ![]() $\textrm {SO}(V)$, where
$\textrm {SO}(V)$, where ![]() $V$ is a three-dimensional quadratic space. So,
$V$ is a three-dimensional quadratic space. So, ![]() $\pi$ can be regarded as an automorphic representation of
$\pi$ can be regarded as an automorphic representation of ![]() $\textrm {SO}(V)$. Moreover,
$\textrm {SO}(V)$. Moreover, ![]() ${\mathbb {Q}}^\times \backslash K^\times \simeq \textrm {SO}(W)$, where
${\mathbb {Q}}^\times \backslash K^\times \simeq \textrm {SO}(W)$, where ![]() $W\subset V$ is a two-dimensional quadratic space; this allows us to view
$W\subset V$ is a two-dimensional quadratic space; this allows us to view ![]() $\chi$ as an automorphic representation
$\chi$ as an automorphic representation ![]() $\pi _0$ on
$\pi _0$ on ![]() $\textrm {SO}(W)$. Under this viewpoint,
$\textrm {SO}(W)$. Under this viewpoint, ![]() $L(s, \pi \times {\mathcal {AI}}(\chi )) = L(s, \pi \boxtimes \pi _0)$ is the standard
$L(s, \pi \times {\mathcal {AI}}(\chi )) = L(s, \pi \boxtimes \pi _0)$ is the standard ![]() $L$-function on
$L$-function on ![]() $\textrm {SO}(V) \times \textrm {SO}(W)$, which puts it into the Gross–Prasad framework.
$\textrm {SO}(V) \times \textrm {SO}(W)$, which puts it into the Gross–Prasad framework.
Finally, we have that
where ![]() $\pi _K$ denotes the base change of
$\pi _K$ denotes the base change of ![]() $\pi$ to
$\pi$ to ![]() $G({\mathbb {A}}_K)$. Thus,
$G({\mathbb {A}}_K)$. Thus, ![]() $L(s , \pi \times {\mathcal {AI}}(\chi ))$ can also be viewed as an
$L(s , \pi \times {\mathcal {AI}}(\chi ))$ can also be viewed as an ![]() $L$-function on
$L$-function on ![]() $D^\times ({\mathbb {A}}_K) \times {\mathbb {A}}_K^\times$ or on
$D^\times ({\mathbb {A}}_K) \times {\mathbb {A}}_K^\times$ or on ![]() $\textrm {GL}_2({\mathbb {A}}_K) \times {\mathbb {A}}_K^\times$.
$\textrm {GL}_2({\mathbb {A}}_K) \times {\mathbb {A}}_K^\times$.
Thus, Theorem 6.2 can be regarded as a subconvexity result for any of the groups ![]() $G({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$,
$G({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$, ![]() $\textrm {GL}_2({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$,
$\textrm {GL}_2({\mathbb {A}}) \times \textrm {GL}_2({\mathbb {A}})$, ![]() $\textrm {SO}(V)({\mathbb {A}})\times \textrm {SO}(W)({\mathbb {A}})$,
$\textrm {SO}(V)({\mathbb {A}})\times \textrm {SO}(W)({\mathbb {A}})$, ![]() $G({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$, and
$G({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$, and ![]() $\textrm {GL}_2({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$. We also note that if
$\textrm {GL}_2({\mathbb {A}}_K) \times \textrm {GL}_1({\mathbb {A}}_K)$. We also note that if ![]() $\chi =\bf 1$ is the trivial character, then
$\chi =\bf 1$ is the trivial character, then ![]() $L(s , \pi \times {\mathcal {AI}}(\mathbf {1})) = L(s , \pi )L(s, \pi \times \rho _K)$. In this special case, we suspect that other existing methods may give a superior exponent in the setting of Theorem 6.2.
$L(s , \pi \times {\mathcal {AI}}(\mathbf {1})) = L(s , \pi )L(s, \pi \times \rho _K)$. In this special case, we suspect that other existing methods may give a superior exponent in the setting of Theorem 6.2.
Remark 6.5 The representation ![]() ${\mathcal {AI}}(\chi )$ can be seen to be generated by the classical theta series (due to Hecke and Maass) associated to Hecke characters on
${\mathcal {AI}}(\chi )$ can be seen to be generated by the classical theta series (due to Hecke and Maass) associated to Hecke characters on ![]() $K^\times \backslash {\mathbb {A}}_K^\times$. More precisely, we can identify a Hecke character
$K^\times \backslash {\mathbb {A}}_K^\times$. More precisely, we can identify a Hecke character ![]() $\chi$ on
$\chi$ on ![]() $K$ of conductor
$K$ of conductor ![]() $\mathbf {m}$ with a character on the group of fractional ideals of
$\mathbf {m}$ with a character on the group of fractional ideals of ![]() $K$ coprime to
$K$ coprime to ![]() $\mathbf {m}$. This allows us to write down explicitly an automorphic newform
$\mathbf {m}$. This allows us to write down explicitly an automorphic newform ![]() $\theta _\chi$ that generates
$\theta _\chi$ that generates ![]() ${\mathcal {AI}}(\chi )$. For example, suppose that
${\mathcal {AI}}(\chi )$. For example, suppose that ![]() $K={\mathbb {Q}}(\sqrt {M})$ is an imaginary quadratic field with
$K={\mathbb {Q}}(\sqrt {M})$ is an imaginary quadratic field with ![]() $M<0$ a fundamental discriminant. Suppose also that
$M<0$ a fundamental discriminant. Suppose also that ![]() $\chi _\infty (\alpha ) = ({\alpha }/{|\alpha |})^\ell$ where
$\chi _\infty (\alpha ) = ({\alpha }/{|\alpha |})^\ell$ where ![]() $\ell \in {\mathbb {Z}}_{\geqslant 0}$ and denote
$\ell \in {\mathbb {Z}}_{\geqslant 0}$ and denote ![]() $Q = N(\mathbf {m})$. Then
$Q = N(\mathbf {m})$. Then ![]() $\theta _\chi$ is the holomorphic newformFootnote 13 of weight
$\theta _\chi$ is the holomorphic newformFootnote 13 of weight ![]() $\ell +1$, level
$\ell +1$, level ![]() $|MQ|$, and character
$|MQ|$, and character ![]() $({M}/{\cdot })$ given by the sum over ideals
$({M}/{\cdot })$ given by the sum over ideals ![]() ${\mathbf {a}}$ as
${\mathbf {a}}$ as
We can write down a similar formula when ![]() $K$ is real; see Appendix A.1 of [Reference Humphries and KhanHK20]. In this case the hypothesis
$K$ is real; see Appendix A.1 of [Reference Humphries and KhanHK20]. In this case the hypothesis ![]() $\chi |_{{\mathbb {A}}^\times } =1$ implies that
$\chi |_{{\mathbb {A}}^\times } =1$ implies that ![]() $\theta _\chi$ is a weight 0 Maass form.
$\theta _\chi$ is a weight 0 Maass form.
For the convenience of the reader, we give a version of Theorem 6.2 that avoids any mention of quaternion algebras and that focusses on a single prime (‘depth aspect’) for simplicity.
Corollary 6.6 Let ![]() $p$ be an odd prime, and
$p$ be an odd prime, and ![]() $d\neq 1$ a positive squarefree integer with an even number of prime factors. Assume that
$d\neq 1$ a positive squarefree integer with an even number of prime factors. Assume that ![]() $(p,d)=1$. Let
$(p,d)=1$. Let ![]() $M<0$ be a fundamental discriminant and put
$M<0$ be a fundamental discriminant and put ![]() $K={\mathbb {Q}}(\sqrt {M})$. Assume that
$K={\mathbb {Q}}(\sqrt {M})$. Assume that ![]() $({M}/{p}) = 1$ and
$({M}/{p}) = 1$ and ![]() $({M}/{q}) = -1$ for all primes
$({M}/{q}) = -1$ for all primes ![]() $q$ dividing
$q$ dividing ![]() $d$. Let
$d$. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $K^\times \backslash {\mathbb {A}}_K^\times$ such that
$K^\times \backslash {\mathbb {A}}_K^\times$ such that ![]() $\chi |_{{\mathbb {A}}^\times } = 1$ and such that
$\chi |_{{\mathbb {A}}^\times } = 1$ and such that ![]() $\gcd (C(\chi ), d)=1$, where
$\gcd (C(\chi ), d)=1$, where ![]() $C(\chi )= N(\textrm {cond}(\chi ))$. Let
$C(\chi )= N(\textrm {cond}(\chi ))$. Let ![]() $f$ be either a holomorphic cuspform of weight
$f$ be either a holomorphic cuspform of weight ![]() $k \geqslant 2$ or a Maass cuspform of weight
$k \geqslant 2$ or a Maass cuspform of weight ![]() $0$ and eigenvalue
$0$ and eigenvalue ![]() $\lambda$ with respect to the subgroup
$\lambda$ with respect to the subgroup ![]() $\Gamma _0(dp^n)$ and assume that
$\Gamma _0(dp^n)$ and assume that ![]() $f$ is a newform (of trivial nebentypus). Then we have
$f$ is a newform (of trivial nebentypus). Then we have
Proof. Let ![]() $\pi '$ be the automorphic representation attached to
$\pi '$ be the automorphic representation attached to ![]() $f$. Note that
$f$. Note that ![]() $\pi '$ is (up to a twist) a Steinberg representation at each prime dividing
$\pi '$ is (up to a twist) a Steinberg representation at each prime dividing ![]() $d$. We let
$d$. We let ![]() $D$ be the indefinite quaternion division algebra of reduced discriminant
$D$ be the indefinite quaternion division algebra of reduced discriminant ![]() $d$. Then
$d$. Then ![]() $\pi '$ transfers to an automorphic representation
$\pi '$ transfers to an automorphic representation ![]() $\pi \in \mathcal {S}_p$ on
$\pi \in \mathcal {S}_p$ on ![]() $D^\times ({\mathbb {A}})$. The corollary now follows immediately from Theorem 6.2.
$D^\times ({\mathbb {A}})$. The corollary now follows immediately from Theorem 6.2.
6.2 An explicit version of Waldspurger's formula
We now begin the proof of Theorem 6.2. We assume the conditions of Theorem 6.2 for the rest of this section. Let ![]() $\pi = \otimes _v \pi _v \in \mathcal {S}_P$. Then, for all finite primes
$\pi = \otimes _v \pi _v \in \mathcal {S}_P$. Then, for all finite primes ![]() $p$,
$p$, ![]() $\pi _p$ has a
$\pi _p$ has a ![]() $\chi _p$-Waldspurger model; this follows, e.g., from the calculations of § 5 of [Reference GrossGro88]. We may further assume that
$\chi _p$-Waldspurger model; this follows, e.g., from the calculations of § 5 of [Reference GrossGro88]. We may further assume that ![]() $\pi _\infty$ has a
$\pi _\infty$ has a ![]() $\chi _\infty$-Waldspurger model, since otherwise the global
$\chi _\infty$-Waldspurger model, since otherwise the global ![]() $\epsilon$-factor
$\epsilon$-factor ![]() $\epsilon (\pi \times {\mathcal {AI}}(\chi ))$ would equal
$\epsilon (\pi \times {\mathcal {AI}}(\chi ))$ would equal ![]() $-1$ and we would have
$-1$ and we would have ![]() $L(1/2, \pi \times {\mathcal {AI}}(\chi )) =0$, making Theorem 6.2 trivial.
$L(1/2, \pi \times {\mathcal {AI}}(\chi )) =0$, making Theorem 6.2 trivial.
Since all primes dividing ![]() $d$ are inert in
$d$ are inert in ![]() $K$, it follows that
$K$, it follows that ![]() $K$ embeds in
$K$ embeds in ![]() $D$. We fix an embedding
$D$. We fix an embedding ![]() $\Phi :K \hookrightarrow D$ and let
$\Phi :K \hookrightarrow D$ and let ![]() $T = \Phi (K^\times ) \simeq K^\times$ be the corresponding torus inside
$T = \Phi (K^\times ) \simeq K^\times$ be the corresponding torus inside ![]() $G$. We henceforth consider
$G$. We henceforth consider ![]() $\chi$ as a character of
$\chi$ as a character of ![]() ${\mathbb {A}}^\times T({\mathbb {Q}})\backslash T({\mathbb {A}}^\times )$. Given any
${\mathbb {A}}^\times T({\mathbb {Q}})\backslash T({\mathbb {A}}^\times )$. Given any ![]() $\phi \in V_\pi$, consider the period integral
$\phi \in V_\pi$, consider the period integral
where ![]() $dt$ is the product of local Tamagawa measures. Also, for this section only, we let the measure on
$dt$ is the product of local Tamagawa measures. Also, for this section only, we let the measure on ![]() $G({\mathbb {A}})$ be the product of the local Tamagawa measures and define
$G({\mathbb {A}})$ be the product of the local Tamagawa measures and define ![]() $\langle \phi , \phi \rangle$ with respect to this measure. A beautiful formula of Waldspurger [Reference WaldspurgerWal85] states that
$\langle \phi , \phi \rangle$ with respect to this measure. A beautiful formula of Waldspurger [Reference WaldspurgerWal85] states that
 \[ \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} = \zeta(2) \frac{L(1/2, \pi \times {\mathcal{AI}}(\chi)) }{L(1, \pi, \textrm{Ad})} \prod_v \alpha_v(K, \chi, \phi), \]
\[ \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} = \zeta(2) \frac{L(1/2, \pi \times {\mathcal{AI}}(\chi)) }{L(1, \pi, \textrm{Ad})} \prod_v \alpha_v(K, \chi, \phi), \]
where the ![]() $\alpha _v(K, \chi , \phi )$ are local integrals which equal 1 at almost all places
$\alpha _v(K, \chi , \phi )$ are local integrals which equal 1 at almost all places ![]() $v$. There have been several papers which have explicitly computed these local integrals at the remaining (ramified) places under certain assumptions, leading to an explicit Waldspurger formula in those cases. We will need such an explicit formula which applies to our setup, due to File et al. [Reference File, Martin and PitaleFMP17].
$v$. There have been several papers which have explicitly computed these local integrals at the remaining (ramified) places under certain assumptions, leading to an explicit Waldspurger formula in those cases. We will need such an explicit formula which applies to our setup, due to File et al. [Reference File, Martin and PitaleFMP17].
To state the formula, let us first set up some notation. First of all, we choose the embedding ![]() $\Phi :K \hookrightarrow D$ such that
$\Phi :K \hookrightarrow D$ such that ![]() ${\mathcal {O}}_K$ embeds in
${\mathcal {O}}_K$ embeds in ![]() ${\mathcal {O}}^\textrm {max}$ optimally, i.e.
${\mathcal {O}}^\textrm {max}$ optimally, i.e. ![]() $\Phi (K) \cap {\mathcal {O}}^\textrm {max} = \Phi ({\mathcal {O}}_K)$. Note that for each prime
$\Phi (K) \cap {\mathcal {O}}^\textrm {max} = \Phi ({\mathcal {O}}_K)$. Note that for each prime ![]() $p$ we have
$p$ we have ![]() $\Phi (K_p) \cap {\mathcal {O}}_p^\textrm {max} = \Phi ({\mathcal {O}}_{K,p})$, where
$\Phi (K_p) \cap {\mathcal {O}}_p^\textrm {max} = \Phi ({\mathcal {O}}_{K,p})$, where ![]() $K_p = K \otimes _{\mathbb {Q}} {\mathbb {Q}}_p$ and
$K_p = K \otimes _{\mathbb {Q}} {\mathbb {Q}}_p$ and ![]() ${\mathcal {O}}_{K,p} = {\mathcal {O}}_K \otimes _{\mathbb {Z}} {\mathbb {Z}}_p$. Next, we need to specify the automorphic form
${\mathcal {O}}_{K,p} = {\mathcal {O}}_K \otimes _{\mathbb {Z}} {\mathbb {Z}}_p$. Next, we need to specify the automorphic form ![]() $\phi = \otimes _v \phi _v$. For each finite prime
$\phi = \otimes _v \phi _v$. For each finite prime ![]() $p$ that does not divide
$p$ that does not divide ![]() $C(\pi )C(\chi )$, we let
$C(\pi )C(\chi )$, we let ![]() $\phi _p$ be the (unique up to multiples) non-zero vector in
$\phi _p$ be the (unique up to multiples) non-zero vector in ![]() $\pi _p$ that is fixed by
$\pi _p$ that is fixed by ![]() $K_p$.
$K_p$.
Next, let ![]() $p$ be a prime that divides
$p$ be a prime that divides ![]() $C(\chi )$ but does not divide
$C(\chi )$ but does not divide ![]() $C(\pi )$. Define
$C(\pi )$. Define ![]() $m_p$ to be the largest positive integer such that
$m_p$ to be the largest positive integer such that ![]() $p^{m_p} | C(\chi )$ and put
$p^{m_p} | C(\chi )$ and put ![]() $c_p = \lceil {m_p}/{2} \rceil$. (In fact,
$c_p = \lceil {m_p}/{2} \rceil$. (In fact, ![]() $m_p$ is always even, but we will not need this fact). Note that the character
$m_p$ is always even, but we will not need this fact). Note that the character ![]() $\chi _p$ on
$\chi _p$ on ![]() $K_p^\times$ is trivial on the subgroup
$K_p^\times$ is trivial on the subgroup ![]() ${\mathbb {Z}}_p^\times + p^{c_p} {\mathcal {O}}_{K,p}$. Now, by § 3 of [Reference GrossGro88], there exists a maximal order
${\mathbb {Z}}_p^\times + p^{c_p} {\mathcal {O}}_{K,p}$. Now, by § 3 of [Reference GrossGro88], there exists a maximal order ![]() $R_p$ of
$R_p$ of ![]() $D_p$ such that
$D_p$ such that ![]() $R_p \cap \Phi (K_p) = {\mathbb {Z}}_p + p^{c_p} \Phi ({\mathcal {O}}_{K,p})$. We let
$R_p \cap \Phi (K_p) = {\mathbb {Z}}_p + p^{c_p} \Phi ({\mathcal {O}}_{K,p})$. We let ![]() $\phi _p$ be the unique (up to multiples) vector in
$\phi _p$ be the unique (up to multiples) vector in ![]() $\pi _p$ that is fixed by
$\pi _p$ that is fixed by ![]() $R_p^\times$. Note that
$R_p^\times$. Note that ![]() $R_p^\times$ is conjugate to
$R_p^\times$ is conjugate to ![]() $K_p$; hence,
$K_p$; hence, ![]() $\phi _p$ is a
$\phi _p$ is a ![]() $G_p$-translate of the unique (up to multiples)
$G_p$-translate of the unique (up to multiples) ![]() $K_p$-fixed vector (spherical vector) in
$K_p$-fixed vector (spherical vector) in ![]() $\pi _p$.
$\pi _p$.
Next, let ![]() $p$ be a prime that divides
$p$ be a prime that divides ![]() $C(\pi )$. Note that
$C(\pi )$. Note that ![]() $K_p \simeq {\mathbb {Q}}_p \oplus {\mathbb {Q}}_p$. Define
$K_p \simeq {\mathbb {Q}}_p \oplus {\mathbb {Q}}_p$. Define ![]() $c_p$ as above and define
$c_p$ as above and define ![]() $n_p = a(\pi _p)$, so that
$n_p = a(\pi _p)$, so that ![]() $n_p$ is the largest positive integer such that
$n_p$ is the largest positive integer such that ![]() $p^{n_p} | C(\pi )$. Let
$p^{n_p} | C(\pi )$. Let ![]() $K_0(n_p)$ be as usual the subgroup of
$K_0(n_p)$ be as usual the subgroup of ![]() $\textrm {GL}_2({\mathbb {Z}}_p)$ consisting of matrices that are upper triangular modulo
$\textrm {GL}_2({\mathbb {Z}}_p)$ consisting of matrices that are upper triangular modulo ![]() $p^{n_p}$. Take
$p^{n_p}$. Take ![]() $g_p \in G_p$ such that
$g_p \in G_p$ such that ![]() $\iota _p(g_p^{-1}T({\mathbb {Q}}_p)g_p)$ is the diagonal subgroup of
$\iota _p(g_p^{-1}T({\mathbb {Q}}_p)g_p)$ is the diagonal subgroup of ![]() $\textrm {GL}_2({\mathbb {Q}}_p)$. Define the subgroup
$\textrm {GL}_2({\mathbb {Q}}_p)$. Define the subgroup ![]() $K'_0(n_p)$ of
$K'_0(n_p)$ of ![]() $G_p$ via
$G_p$ via
and let ![]() $\phi _p$ be the unique (up to multiples) vector in
$\phi _p$ be the unique (up to multiples) vector in ![]() $\pi _p$ that is fixed by
$\pi _p$ that is fixed by ![]() $K'_0(n_p)$. Note that
$K'_0(n_p)$. Note that ![]() $\phi _p$ is a
$\phi _p$ is a ![]() $G_p$-translate of the unique (up to multiples) newvector in
$G_p$-translate of the unique (up to multiples) newvector in ![]() $\pi _p$.
$\pi _p$.
Finally, we define ![]() $\phi _\infty$. Let
$\phi _\infty$. Let ![]() $K_\infty$ be a maximal compact connected subgroup of
$K_\infty$ be a maximal compact connected subgroup of ![]() $D_\infty$ whose restriction to
$D_\infty$ whose restriction to ![]() $T({\mathbb {R}})$ is a maximal compact connected subgroup of
$T({\mathbb {R}})$ is a maximal compact connected subgroup of ![]() $T({\mathbb {R}})$. Let
$T({\mathbb {R}})$. Let ![]() $\phi _\infty$ be a vector of minimal (non-negative) weight such that
$\phi _\infty$ be a vector of minimal (non-negative) weight such that ![]() $\pi _\infty (t_\infty ) \phi _\infty = \chi _\infty (t_\infty ) \phi _\infty$ for all
$\pi _\infty (t_\infty ) \phi _\infty = \chi _\infty (t_\infty ) \phi _\infty$ for all ![]() $t_\infty \in K_\infty \cap T({\mathbb {R}})$.
$t_\infty \in K_\infty \cap T({\mathbb {R}})$.
Put ![]() $\phi = \otimes _v \phi _v$. For brevity, put
$\phi = \otimes _v \phi _v$. For brevity, put ![]() $N=C(\pi )$,
$N=C(\pi )$, ![]() $Q=C(\chi )$. Then we have the following explicit version of Waldspurger's formula due to File et al. (Theorem 1.1 of [Reference File, Martin and PitaleFMP17]), simplified to our setting:
$Q=C(\chi )$. Then we have the following explicit version of Waldspurger's formula due to File et al. (Theorem 1.1 of [Reference File, Martin and PitaleFMP17]), simplified to our setting:
 \begin{equation} \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} = \frac{C_\infty\zeta(2)}{2\sqrt{Q\textrm{disc}(K})} \prod_{p|Q} L(1, \rho_{K,p})^2 \prod_{p|N} \bigg(1+\frac{1}{p}\bigg) \prod_{p|d} \bigg(1-\frac{1}{p}\bigg) \frac{L^{Nd}(1/2, \pi \times {\mathcal{AI}}(\chi)) }{L^{Nd}(1, \pi, \textrm{Ad})}. \end{equation}
\begin{equation} \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} = \frac{C_\infty\zeta(2)}{2\sqrt{Q\textrm{disc}(K})} \prod_{p|Q} L(1, \rho_{K,p})^2 \prod_{p|N} \bigg(1+\frac{1}{p}\bigg) \prod_{p|d} \bigg(1-\frac{1}{p}\bigg) \frac{L^{Nd}(1/2, \pi \times {\mathcal{AI}}(\chi)) }{L^{Nd}(1, \pi, \textrm{Ad})}. \end{equation}
Above, ![]() $L^{Nd}$ denotes the
$L^{Nd}$ denotes the ![]() $L$-functions where we omit the Euler factors at primes dividing
$L$-functions where we omit the Euler factors at primes dividing ![]() $Nd$,
$Nd$, ![]() $\rho _K$ denotes the quadratic character associated to
$\rho _K$ denotes the quadratic character associated to ![]() $K/{\mathbb {Q}}$, and the quantity
$K/{\mathbb {Q}}$, and the quantity ![]() $C_\infty$ is a positive real number written down explicitly in [Reference File, Martin and PitaleFMP17, 7B] that depends only on
$C_\infty$ is a positive real number written down explicitly in [Reference File, Martin and PitaleFMP17, 7B] that depends only on ![]() $\pi _\infty$ and
$\pi _\infty$ and ![]() $\chi _\infty$.
$\chi _\infty$.
6.3 The proof of Theorem 6.2
We continue to use the notation ![]() $N=C(\pi )$,
$N=C(\pi )$, ![]() $Q=C(\chi )$. The explicit formula (62) immediately implies the asymptotic inequality
$Q=C(\chi )$. The explicit formula (62) immediately implies the asymptotic inequality
 \begin{align} \bigg(\frac{\sup_{g \in G({\mathbb{A}})} |\phi(g)|}{\|\phi\|_2} \bigg)^2 &\geqslant \frac{1}{(\operatorname{vol}({\mathbb{A}}^\times T({\mathbb{Q}}) \backslash T({\mathbb{A}}))^2} \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} \nonumber\\ &\gg_{K, P, \pi_\infty, \chi_\infty, \epsilon} \frac{1}{\sqrt{Q}} (QN)^{-\epsilon} L(1/2, \pi \times {\mathcal{AI}}(\chi)). \end{align}
\begin{align} \bigg(\frac{\sup_{g \in G({\mathbb{A}})} |\phi(g)|}{\|\phi\|_2} \bigg)^2 &\geqslant \frac{1}{(\operatorname{vol}({\mathbb{A}}^\times T({\mathbb{Q}}) \backslash T({\mathbb{A}}))^2} \frac{|P(\phi)|^2}{\langle \phi, \phi \rangle} \nonumber\\ &\gg_{K, P, \pi_\infty, \chi_\infty, \epsilon} \frac{1}{\sqrt{Q}} (QN)^{-\epsilon} L(1/2, \pi \times {\mathcal{AI}}(\chi)). \end{align} On the other hand, our choice of ![]() $\phi$ implies that
$\phi$ implies that ![]() $\phi _p$ is a translate of the local newvector at all primes
$\phi _p$ is a translate of the local newvector at all primes ![]() $p$. Hence,
$p$. Hence, ![]() $\phi = R(g) \phi '$, where
$\phi = R(g) \phi '$, where ![]() $g \in G({\mathbb {A}}_{\mathbf {f}})$ and
$g \in G({\mathbb {A}}_{\mathbf {f}})$ and ![]() $({\mathbb {C}}\phi ', \pi ) \in {\mathcal {A}}(G, \mathcal {G})$ with
$({\mathbb {C}}\phi ', \pi ) \in {\mathcal {A}}(G, \mathcal {G})$ with ![]() $\mathcal {G}$ as in Proposition 3.14. Furthermore,
$\mathcal {G}$ as in Proposition 3.14. Furthermore, ![]() $\phi _\infty = \phi '_\infty$ is a vector of weight
$\phi _\infty = \phi '_\infty$ is a vector of weight ![]() $k$, where
$k$, where ![]() $k$ depends only on
$k$ depends only on ![]() $\chi _\infty$. Since the sup-norm does not change under translation, we have, using Corollary 4.9,
$\chi _\infty$. Since the sup-norm does not change under translation, we have, using Corollary 4.9,
Combining (63) and (64), we obtain
as desired.
Acknowledgements
We thank Farrell Brumley, Félicien Comtat, and Peter Humphries for helpful comments on an earlier draft of this work, and Paul Nelson for useful discussions. We thank the anonymous referee for several corrections and comments which have improved this paper. A.S. acknowledges the support of the Leverhulme Trust Research Project Grant RPG-2018-401.