We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We discuss, in a non-Archimedean setting, the distribution of the coefficients of L-polynomials of curves of genus g over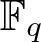 
$\mathbb{F}_q$. Among other results, this allows us to prove that the 
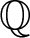$\mathbb{Q}$-vector space spanned by such characteristic polynomials has dimension g + 1. We also state a conjecture about the Archimedean distribution of the number of rational points of curves over finite fields.
