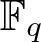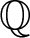1. Introduction
Let ![]() $\mathbb{F}_q$ be a finite field of characteristic p and order
$\mathbb{F}_q$ be a finite field of characteristic p and order ![]() $q=p^f$. For every
$q=p^f$. For every ![]() $g \geq 1$, we let
$g \geq 1$, we let ![]() $\mathcal{M}_g(\mathbb{F}_q)$ be the set of smooth projective curves of genus g over
$\mathcal{M}_g(\mathbb{F}_q)$ be the set of smooth projective curves of genus g over ![]() $\mathbb{F}_q$, up to isomorphism over
$\mathbb{F}_q$, up to isomorphism over ![]() $\mathbb{F}_q$. Recall that, given a (smooth projective) curve
$\mathbb{F}_q$. Recall that, given a (smooth projective) curve ![]() $C/\mathbb{F}_q$, one may introduce its zeta function
$C/\mathbb{F}_q$, one may introduce its zeta function
 \begin{equation*}
Z(C/\mathbb{F}_q,s) = \exp\left( \sum_{m \geq 1} \frac{\#C(\mathbb{F}_{q^m})}{m} q^{-ms} \right),
\end{equation*}
\begin{equation*}
Z(C/\mathbb{F}_q,s) = \exp\left( \sum_{m \geq 1} \frac{\#C(\mathbb{F}_{q^m})}{m} q^{-ms} \right),
\end{equation*} and that by work of Schmidt [Reference Schmidt46] and Weil [Reference Weil51] we know that ![]() $Z(C/\mathbb{F}_q,s)$ is a rational function of
$Z(C/\mathbb{F}_q,s)$ is a rational function of ![]() $t := q^{-s}$. More precisely, we can write
$t := q^{-s}$. More precisely, we can write
 \begin{equation*}
Z(C/\mathbb{F}_q,s)=\frac{P_C(t)}{(1-t)(1-qt)},
\end{equation*}
\begin{equation*}
Z(C/\mathbb{F}_q,s)=\frac{P_C(t)}{(1-t)(1-qt)},
\end{equation*} where ![]() $P_{C}(t)$ is a polynomial (often called the L-polynomial of C) that satisfies the following:
$P_{C}(t)$ is a polynomial (often called the L-polynomial of C) that satisfies the following:
(1)
 $P_{C}(t)$ has integral coefficients and
$P_{C}(t)$ has integral coefficients and  $P_{C}(0)=1$;
$P_{C}(0)=1$;(2)
 $\deg P_{C}(t)=2g$, where
$\deg P_{C}(t)=2g$, where  $g=g(C)$ is the genus of C;
$g=g(C)$ is the genus of C;(3) writing
 $P_{C}(t)=\sum_{i=0}^{2g} a_i t^i$ we have the symmetry relations
$P_{C}(t)=\sum_{i=0}^{2g} a_i t^i$ we have the symmetry relations  $a_{g+i}=q^ia_{g-i}$ for every
$a_{g+i}=q^ia_{g-i}$ for every  $i=0,\ldots,g$.
$i=0,\ldots,g$.
Our main object of interest in this article is the set of L-polynomials of all the curves of a given genus over a finite field ![]() $\mathbb{F}_q$:
$\mathbb{F}_q$:
Definition 1.2. Given a finite field ![]() $\mathbb{F}_q$ and a positive integer g we define
$\mathbb{F}_q$ and a positive integer g we define
 \begin{equation*}
\mathcal{P}_g(\mathbb{F}_q) := \{P_C(t) \, \bigm\vert \, C \in \mathcal{M}_g(\mathbb{F}_q) \}.
\end{equation*}
\begin{equation*}
\mathcal{P}_g(\mathbb{F}_q) := \{P_C(t) \, \bigm\vert \, C \in \mathcal{M}_g(\mathbb{F}_q) \}.
\end{equation*} We will focus in particular on the non-Archimedean distribution of these L-polynomials. For a fixed integer ![]() $N \geq 2$, upon reduction modulo N one obtains from
$N \geq 2$, upon reduction modulo N one obtains from ![]() $\mathcal{P}_g(\mathbb{F}_q)$ a set
$\mathcal{P}_g(\mathbb{F}_q)$ a set ![]() $\mathcal{P}_{g, N}(\mathbb{F}_q)$ of polynomials in
$\mathcal{P}_{g, N}(\mathbb{F}_q)$ of polynomials in ![]() $(\mathbb{Z}/N\mathbb{Z})[t]$. Considering this set of reduced polynomials both for a fixed value of q and in the limit
$(\mathbb{Z}/N\mathbb{Z})[t]$. Considering this set of reduced polynomials both for a fixed value of q and in the limit ![]() $q \to \infty$, we obtain results in three different but related directions:
$q \to \infty$, we obtain results in three different but related directions:
1. We adapt results of Katz–Sarnak from the Archimedean to the non-Archimedean setting, obtaining equidistribution statements for
 $\mathcal{P}_{g, N}(\mathbb{F}_q)$ as
$\mathcal{P}_{g, N}(\mathbb{F}_q)$ as  $q \to \infty$ (theorem 2.1). While special instances of this result appear in the literature (especially for the case of elliptic curves, see [Reference Castryck and Hubrechts13, Reference Gekeler23]), the general case does not seem to have been explored previously—though see [Reference Achter2] for related results.
$q \to \infty$ (theorem 2.1). While special instances of this result appear in the literature (especially for the case of elliptic curves, see [Reference Castryck and Hubrechts13, Reference Gekeler23]), the general case does not seem to have been explored previously—though see [Reference Achter2] for related results.2. The previous result allows us to disprove a recent conjecture by Bergström–Howe–Lorenzo García–Ritzenthaler [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] about the Archimedean distribution of the number of rational points of non-hyperelliptic curves over finite fields (see proposition 3.6 and the discussion before it). Theorem 2.1, combined with the general Lang–Trotter philosophy, leads us to propose a new conjecture (conjecture 3.4), which seems both more natural (in view of the general principles that seem to regulate statistical phenomena in arithmetic) and in better accord with the numerical evidence (see §3.2).
3. Finally, theorem 2.1 easily implies that, for a fixed genus g and for
 $q \gg_g 1$, the set
$q \gg_g 1$, the set  $\mathcal{P}_g(\mathbb{F}_q)$ spans a
$\mathcal{P}_g(\mathbb{F}_q)$ spans a  $\mathbb{Q}$-vector space of dimension g + 1 (remark 2.9). By considering more carefully the set
$\mathbb{Q}$-vector space of dimension g + 1 (remark 2.9). By considering more carefully the set  $\mathcal{P}_{g, 2}(\mathbb{F}_q)$ for every fixed value of q, we are able to prove that this statement does, in fact, hold for all pairs (g, q) (theorem 1.4), thus confirming a conjecture of Kaczorowski and Perelli [Reference Kaczorowski and Perelli28, remark 8]. The proof is based on properties of L-polynomials modulo 2 which have also recently been explored, with different aims, in [Reference Costa, Donepudi, Fernando, Karemaker, Springer and West16]. Using theorem 2.1, we can also obtain an asymptotic result for non-linear relations among the coefficients of elements of
$\mathcal{P}_{g, 2}(\mathbb{F}_q)$ for every fixed value of q, we are able to prove that this statement does, in fact, hold for all pairs (g, q) (theorem 1.4), thus confirming a conjecture of Kaczorowski and Perelli [Reference Kaczorowski and Perelli28, remark 8]. The proof is based on properties of L-polynomials modulo 2 which have also recently been explored, with different aims, in [Reference Costa, Donepudi, Fernando, Karemaker, Springer and West16]. Using theorem 2.1, we can also obtain an asymptotic result for non-linear relations among the coefficients of elements of  $\mathcal{P}_g(\mathbb{F}_q)$, see theorem 6.1.
$\mathcal{P}_g(\mathbb{F}_q)$, see theorem 6.1.
Recently, much attention has been devoted to questions close to those that we consider here: in addition to the aforementioned [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9], we also refer the reader to [Reference Achter, Erman, Kedlaya, Wood and Zureick-Brown4], as well as [Reference Achter, Altuğ, Garcia and Gordon3, Reference Ma42], and [Reference Shmakov49]. We discuss some relations between our work and these latter articles in remark 3.15. We believe that different parts of the mathematical community are approaching the same questions we discuss in this article from complementary perspectives, and we hope that the present work will also encourage a fruitful exchange of ideas between these different points of view.
For this introduction, we focus more specifically on our contributions. The non-Archimedean behaviour of the L-polynomials is closely related to the (geometric version of the) Chebotarev density theorem, in the following sense. Let ![]() $\mathcal{C} \xrightarrow{\pi} S \to \operatorname{Spec} \mathbb{Z}$ be a versal family of curves of genus g, that is, a family in which every isomorphism class of curves of genus g appears at least once (we use the tri-canonically embedded family, see §2 for details). Considering the N-torsion sections of
$\mathcal{C} \xrightarrow{\pi} S \to \operatorname{Spec} \mathbb{Z}$ be a versal family of curves of genus g, that is, a family in which every isomorphism class of curves of genus g appears at least once (we use the tri-canonically embedded family, see §2 for details). Considering the N-torsion sections of ![]() $\operatorname{Jac} \mathcal{C} \to S$ gives rise to a Galois cover
$\operatorname{Jac} \mathcal{C} \to S$ gives rise to a Galois cover ![]() $S' \to S$ whose Galois group GN is a subgroup of
$S' \to S$ whose Galois group GN is a subgroup of ![]() $\operatorname{GL}_{2g}(\mathbb{Z}/N\mathbb{Z})$—essentially, Sʹ is the minimal cover of S over which all the N-torsion sections of
$\operatorname{GL}_{2g}(\mathbb{Z}/N\mathbb{Z})$—essentially, Sʹ is the minimal cover of S over which all the N-torsion sections of ![]() $\operatorname{Jac} \mathcal{C}$ are defined. For every closed point
$\operatorname{Jac} \mathcal{C}$ are defined. For every closed point ![]() $s \in S$, we have a curve Cs, defined over the finite field
$s \in S$, we have a curve Cs, defined over the finite field ![]() $\kappa(s)$, and a Frobenius element
$\kappa(s)$, and a Frobenius element ![]() $\operatorname{Frob}_{s, N} \in G_N$. Note that this Frobenius is an element of the Galois group of the cover and is determined by the property of inducing the finite-field Frobenius
$\operatorname{Frob}_{s, N} \in G_N$. Note that this Frobenius is an element of the Galois group of the cover and is determined by the property of inducing the finite-field Frobenius ![]() $t \mapsto t^{(\#\kappa(s))}$ on the residue field at a point
$t \mapsto t^{(\#\kappa(s))}$ on the residue field at a point ![]() $s' \in S^{\prime}$ lying over s. As usual,
$s' \in S^{\prime}$ lying over s. As usual, ![]() $\operatorname{Frob}_{s, N}$ is only well defined up to conjugacy, or equivalently, up to the choice of the point
$\operatorname{Frob}_{s, N}$ is only well defined up to conjugacy, or equivalently, up to the choice of the point ![]() $s' \in S^{\prime}$ lying over s. The reduction modulo N of the L-polynomial of Cs is determined by the characteristic polynomial of
$s' \in S^{\prime}$ lying over s. The reduction modulo N of the L-polynomial of Cs is determined by the characteristic polynomial of ![]() $\operatorname{Frob}_{s, N}$, so equidistribution results for
$\operatorname{Frob}_{s, N}$, so equidistribution results for ![]() $\operatorname{Frob}_{s, N}$ translate into equidistribution results for
$\operatorname{Frob}_{s, N}$ translate into equidistribution results for ![]() $P_{C} \bmod N$. We make this precise in §2, using Deligne and Katz’s equidistribution theorem instead of Chebotarev’s.
$P_{C} \bmod N$. We make this precise in §2, using Deligne and Katz’s equidistribution theorem instead of Chebotarev’s.
Having precise control over the non-Archimedean distribution of L-polynomials is sufficient to show that the values of ![]() $F_q(t) = \#\{C : C \in \mathcal{M}_g(\mathbb{F}_q), \#C(\mathbb{F}_q)=t \}$ show significant local oscillations—consecutive values of
$F_q(t) = \#\{C : C \in \mathcal{M}_g(\mathbb{F}_q), \#C(\mathbb{F}_q)=t \}$ show significant local oscillations—consecutive values of ![]() $t \in \mathbb{N}$ can correspond to wildly different values of
$t \in \mathbb{N}$ can correspond to wildly different values of ![]() $F_q(t)$. As already mentioned, we use this to disprove [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1].
$F_q(t)$. As already mentioned, we use this to disprove [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1].
We propose a new conjecture that takes these local oscillations into account to compute ![]() $F_q(t)$ (we achieve this by introducing a suitable product of local factors). Here we give an informal statement: for a precise version, see conjecture 3.4 and remark 3.8 for an interpretation of the quantity
$F_q(t)$ (we achieve this by introducing a suitable product of local factors). Here we give an informal statement: for a precise version, see conjecture 3.4 and remark 3.8 for an interpretation of the quantity ![]() $\nu_\ell(q,t)$. See also the remarks after conjecture 3.4 for a more extended discussion of the motivation behind this conjecture.
$\nu_\ell(q,t)$. See also the remarks after conjecture 3.4 for a more extended discussion of the motivation behind this conjecture.
Conjecture 1.3
Let ![]() $g\geq 1$ and q be a prime power. Let
$g\geq 1$ and q be a prime power. Let ![]() $H'(q,t)$ be the ‘probability’ that a curve
$H'(q,t)$ be the ‘probability’ that a curve ![]() $C/\mathbb{F}_q$ of genus g has
$C/\mathbb{F}_q$ of genus g has ![]() $q+1-t$ rational points. Given a prime
$q+1-t$ rational points. Given a prime ![]() $\ell$ define
$\ell$ define ![]() $\nu_\ell(q,t)$ as the ‘normalized probability that a matrix
$\nu_\ell(q,t)$ as the ‘normalized probability that a matrix ![]() $M\in \operatorname{GSp}_{2g}(\mathbb{Z}_\ell)$ with multiplier q has trace t’ (see Eqs. (7) and (8) for a precise definition). Let
$M\in \operatorname{GSp}_{2g}(\mathbb{Z}_\ell)$ with multiplier q has trace t’ (see Eqs. (7) and (8) for a precise definition). Let ![]() $\nu_\infty(q,t)=\operatorname{ST}_g(t/\sqrt{q})$, where
$\nu_\infty(q,t)=\operatorname{ST}_g(t/\sqrt{q})$, where ![]() $\operatorname{ST}_g$ is the Sato–Tate measure in dimension g. Let
$\operatorname{ST}_g$ is the Sato–Tate measure in dimension g. Let ![]() $\nu^{\prime}(q,\cdot)$ be the measure
$\nu^{\prime}(q,\cdot)$ be the measure ![]() $c\cdot\nu_\infty(q,\cdot)\prod_{\ell \lt \infty}\nu_\ell(q,\cdot)$, where c is the normalization constant that ensures that
$c\cdot\nu_\infty(q,\cdot)\prod_{\ell \lt \infty}\nu_\ell(q,\cdot)$, where c is the normalization constant that ensures that ![]() $\nu^{\prime}$ has total mass 1 (i.e., that it is a probability measure). The L 1-distance between
$\nu^{\prime}$ has total mass 1 (i.e., that it is a probability measure). The L 1-distance between ![]() $H'(q,\cdot)$ and
$H'(q,\cdot)$ and ![]() $\nu^{\prime}(q,\cdot)$ tends to 0 as
$\nu^{\prime}(q,\cdot)$ tends to 0 as ![]() $q \to \infty$.
$q \to \infty$.
Finally, theorem 1.4 answers the following natural question: does lemma 1.1 capture all the (linear) relations among the coefficients of the polynomials ![]() $P_C(t)$? In other words, what is the dimension of the
$P_C(t)$? In other words, what is the dimension of the ![]() $\mathbb{Q}$-vector subspace of
$\mathbb{Q}$-vector subspace of ![]() $\mathbb{Q}[t]$ spanned by the polynomials in
$\mathbb{Q}[t]$ spanned by the polynomials in ![]() $\mathcal{P}_g(\mathbb{F}_q)$? As a consequence of lemma 1.1, it is immediate to see that this space has dimension at most g + 1. Equality holds if and only if all the linear relations among the coefficients are already listed in lemma 1.1. We show that equality does in fact hold for all genera and all finite fields: this extends work of Birch [Reference Birch10] for curves of genus 1 and of Howe–Nart–Ritzenthaler [Reference Howe, Nart and Ritzenthaler27] for curves of genus 2 and confirms the aforementioned conjecture of Kaczorowski and Perelli [Reference Kaczorowski and Perelli28, remark 8]:
$\mathcal{P}_g(\mathbb{F}_q)$? As a consequence of lemma 1.1, it is immediate to see that this space has dimension at most g + 1. Equality holds if and only if all the linear relations among the coefficients are already listed in lemma 1.1. We show that equality does in fact hold for all genera and all finite fields: this extends work of Birch [Reference Birch10] for curves of genus 1 and of Howe–Nart–Ritzenthaler [Reference Howe, Nart and Ritzenthaler27] for curves of genus 2 and confirms the aforementioned conjecture of Kaczorowski and Perelli [Reference Kaczorowski and Perelli28, remark 8]:
Theorem 1.4. Let p be a prime, let ![]() $f \geq 1$, and denote by
$f \geq 1$, and denote by ![]() $\mathbb{F}_q$ the finite field with
$\mathbb{F}_q$ the finite field with ![]() $q=p^f$ elements. Let
$q=p^f$ elements. Let ![]() $\mathcal{P}_g(\mathbb{F}_q)$ be as in definition 1.2 and let
$\mathcal{P}_g(\mathbb{F}_q)$ be as in definition 1.2 and let ![]() $L_g(\mathbb{F}_q)$ be the
$L_g(\mathbb{F}_q)$ be the ![]() $\mathbb{Q}$-vector subspace of
$\mathbb{Q}$-vector subspace of ![]() $\mathbb{Q}[t]$ spanned by
$\mathbb{Q}[t]$ spanned by ![]() $\mathcal{P}_g(\mathbb{F}_q)$. We have
$\mathcal{P}_g(\mathbb{F}_q)$. We have
The proof is based on the following observation: in order to establish the linear independence of a set of polynomials with integral coefficients, it is certainly enough to show that they are linearly independent modulo 2. In the case of the L-polynomial of a curve C, the reduction modulo 2 can be read off the action of Galois on the set of 2-torsion points of the Jacobian of C. In turn, when C is hyperelliptic, this action is easy to write down explicitly in terms of a defining equation of C: one can then find g + 1 curves whose L-polynomials form a basis of ![]() $L_g(\mathbb{F}_q)$. Since the properties of the 2-torsion points are slightly different depending on whether the characteristic is odd or even, we split our proof into two parts, one for the case p odd and one for the case p = 2. We remark in particular that our proof is constructive: we explicitly give g + 1 curves whose L-polynomials form a basis of
$L_g(\mathbb{F}_q)$. Since the properties of the 2-torsion points are slightly different depending on whether the characteristic is odd or even, we split our proof into two parts, one for the case p odd and one for the case p = 2. We remark in particular that our proof is constructive: we explicitly give g + 1 curves whose L-polynomials form a basis of ![]() $L_g(\mathbb{F}_q)$, see corollary 5.4 for odd p and the proof in §5.2 for p = 2.
$L_g(\mathbb{F}_q)$, see corollary 5.4 for odd p and the proof in §5.2 for p = 2.
We conclude this introduction by briefly describing the structure of the article. In §2, we prove an equidistribution result for ![]() $\mathcal{P}_{g, N}$ (see theorem 2.1). In §3, we state our conjecture on the probability that a curve has a given number of rational points (see conjecture 3.4). We also explain why we believe this conjecture to be true and present some numerical evidence that supports it. We further discuss the difficulties that arise in formally defining the quantities involved in the conjecture (see, in particular, remark 3.14). This justifies the work of §4, where we prove some technical results necessary to even state conjecture 3.4. Finally, in §5, we prove theorem 1.4 and in §6 we study non-linear relations among the coefficients of the polynomials in
$\mathcal{P}_{g, N}$ (see theorem 2.1). In §3, we state our conjecture on the probability that a curve has a given number of rational points (see conjecture 3.4). We also explain why we believe this conjecture to be true and present some numerical evidence that supports it. We further discuss the difficulties that arise in formally defining the quantities involved in the conjecture (see, in particular, remark 3.14). This justifies the work of §4, where we prove some technical results necessary to even state conjecture 3.4. Finally, in §5, we prove theorem 1.4 and in §6 we study non-linear relations among the coefficients of the polynomials in ![]() $\mathcal{P}_g(\mathbb{F}_q)$.
$\mathcal{P}_g(\mathbb{F}_q)$.
1.1. Notation and classical results
We fix our notation for symplectic groups:
Definition 1.5. Let ![]() $g \geq 1$ and let R be a commutative ring with identity. Fix a non-degenerate alternating bilinear form on
$g \geq 1$ and let R be a commutative ring with identity. Fix a non-degenerate alternating bilinear form on ![]() $R^{2g}$, represented by the matrix Ω (note that the form is non-degenerate if and only if
$R^{2g}$, represented by the matrix Ω (note that the form is non-degenerate if and only if ![]() $\det \Omega \in R^\times$). The group
$\det \Omega \in R^\times$). The group ![]() $\operatorname{GSp}_{2g}(R)$ is by definition
$\operatorname{GSp}_{2g}(R)$ is by definition
 \begin{equation*}
\operatorname{GSp}_{2g}(R) = \{M \in \operatorname{GL}_{2g}(R) : \exists \lambda \in R^\times \text{such that } {}^t M \Omega M = \lambda \Omega \}.
\end{equation*}
\begin{equation*}
\operatorname{GSp}_{2g}(R) = \{M \in \operatorname{GL}_{2g}(R) : \exists \lambda \in R^\times \text{such that } {}^t M \Omega M = \lambda \Omega \}.
\end{equation*} The multiplier of a matrix ![]() $M \in \operatorname{GSp}_{2g}(R)$ is the uniquely determined
$M \in \operatorname{GSp}_{2g}(R)$ is the uniquely determined ![]() $\lambda \in R^\times$ such that
$\lambda \in R^\times$ such that ![]() ${}^t M \Omega M = \lambda \Omega$. We denote it by
${}^t M \Omega M = \lambda \Omega$. We denote it by ![]() $\operatorname{mult}(M)$. Given
$\operatorname{mult}(M)$. Given ![]() $q \in R$, we further let
$q \in R$, we further let  $\operatorname{GSp}_{2g}^q(R)$ be the subset of
$\operatorname{GSp}_{2g}^q(R)$ be the subset of ![]() $\operatorname{GSp}_{2g}(R)$ consisting of those matrices that have multiplier equal to q (equality in the group
$\operatorname{GSp}_{2g}(R)$ consisting of those matrices that have multiplier equal to q (equality in the group ![]() $R^\times$).
$R^\times$).
Remark 1.6. We will mostly be interested in the cases ![]() $R=\mathbb{Z}/\ell^n\mathbb{Z}, \mathbb{Z}_\ell$ or
$R=\mathbb{Z}/\ell^n\mathbb{Z}, \mathbb{Z}_\ell$ or ![]() $\mathbb{Q}_\ell$, where
$\mathbb{Q}_\ell$, where ![]() $\ell$ is prime. By definition, the group
$\ell$ is prime. By definition, the group ![]() $\operatorname{GSp}_{2g}(R)$ depends on the choice of Ω, but when R is a local ring, different choices of Ω lead to isomorphic groups [Reference Klingenberg33]. It follows easily that the same is true for
$\operatorname{GSp}_{2g}(R)$ depends on the choice of Ω, but when R is a local ring, different choices of Ω lead to isomorphic groups [Reference Klingenberg33]. It follows easily that the same is true for ![]() $R=\mathbb{Z}/N\mathbb{Z}$ for any integer
$R=\mathbb{Z}/N\mathbb{Z}$ for any integer ![]() $N \geq 2$. When
$N \geq 2$. When ![]() $R \in \{\mathbb{Z}/\ell^n\mathbb{Z}, \mathbb{Z}_\ell, \mathbb{Q}_\ell, \mathbb{Z}/N\mathbb{Z}\}$, we will therefore refer to
$R \in \{\mathbb{Z}/\ell^n\mathbb{Z}, \mathbb{Z}_\ell, \mathbb{Q}_\ell, \mathbb{Z}/N\mathbb{Z}\}$, we will therefore refer to ![]() $\operatorname{GSp}_{2g}(R)$ without necessarily specifying the choice of anti-symmetric form.
$\operatorname{GSp}_{2g}(R)$ without necessarily specifying the choice of anti-symmetric form.
It will be useful to recall the well-known connection between the L-polynomial of a (smooth projective) curve C of genus g and the Galois representations attached to the Jacobian J of C. Let p be a prime, let q be a power of p, and let C be a curve of genus g defined over ![]() $\mathbb{F}_q$. Denote by J the Jacobian of C. Let
$\mathbb{F}_q$. Denote by J the Jacobian of C. Let ![]() $\ell$ be any prime different from p and let
$\ell$ be any prime different from p and let ![]() $T_\ell J$ be the
$T_\ell J$ be the ![]() $\ell$-adic Tate module of J, that is,
$\ell$-adic Tate module of J, that is,
 \begin{equation*}
T_\ell J := \varprojlim_{n} J(\overline{\mathbb{F}_q})[\ell^n].
\end{equation*}
\begin{equation*}
T_\ell J := \varprojlim_{n} J(\overline{\mathbb{F}_q})[\ell^n].
\end{equation*} There is a natural action of ![]() $\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on
$\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on ![]() $T_\ell J$ (induced by the action of
$T_\ell J$ (induced by the action of ![]() $\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on the torsion points of J), and it can be shown that
$\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on the torsion points of J), and it can be shown that ![]() $T_\ell J$ is a free
$T_\ell J$ is a free ![]() $\mathbb{Z}_\ell$-module of rank 2g. Fixing a
$\mathbb{Z}_\ell$-module of rank 2g. Fixing a ![]() $\mathbb{Z}_\ell$-basis of
$\mathbb{Z}_\ell$-basis of ![]() $T_\ell J$, we thus obtain a representation
$T_\ell J$, we thus obtain a representation ![]() $\rho_{\ell^\infty}: \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}_{2g}(\mathbb{Z}_\ell)$ whose image is contained in
$\rho_{\ell^\infty}: \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}_{2g}(\mathbb{Z}_\ell)$ whose image is contained in ![]() $\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell})$; the relevant antisymmetric bilinear form is given by the Weil pairing. Since
$\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell})$; the relevant antisymmetric bilinear form is given by the Weil pairing. Since ![]() $\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ is procyclic, generated by the Frobenius automorphism
$\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ is procyclic, generated by the Frobenius automorphism ![]() $\operatorname{Frob}_q$, we are mostly interested in the action of
$\operatorname{Frob}_q$, we are mostly interested in the action of ![]() $\operatorname{Frob}_q$ on
$\operatorname{Frob}_q$ on ![]() $T_\ell J$, which is captured by its characteristic polynomial
$T_\ell J$, which is captured by its characteristic polynomial
The matrix representing the action of Frobenius is symplectic with multiplier q. Notice that we also have an action of ![]() $\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on the
$\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on the ![]() $\ell$-torsion points of
$\ell$-torsion points of ![]() $J(\overline{\mathbb{F}_q})$, which form an
$J(\overline{\mathbb{F}_q})$, which form an ![]() $\mathbb{F}_\ell$-vector space of dimension 2g; we can thus obtain a mod-
$\mathbb{F}_\ell$-vector space of dimension 2g; we can thus obtain a mod-![]() $\ell$ representation
$\ell$ representation ![]() $\rho_\ell : \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}_{2g}(\mathbb{F}_\ell)$ and a corresponding characteristic polynomial
$\rho_\ell : \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}_{2g}(\mathbb{F}_\ell)$ and a corresponding characteristic polynomial ![]() $f_{C, \ell}(t) = \det(t \operatorname{Id} - \rho_{\ell}(\operatorname{Frob}_q)) \in \mathbb{F}_\ell[t]$. It is clear from the definitions that
$f_{C, \ell}(t) = \det(t \operatorname{Id} - \rho_{\ell}(\operatorname{Frob}_q)) \in \mathbb{F}_\ell[t]$. It is clear from the definitions that ![]() $f_{C, \ell}(t)$ is nothing but the reduction modulo
$f_{C, \ell}(t)$ is nothing but the reduction modulo ![]() $\ell$ of
$\ell$ of ![]() $f_{C, \ell^\infty}(t)$. We can now recall the connection between
$f_{C, \ell^\infty}(t)$. We can now recall the connection between ![]() $P_{C}(t)$ and
$P_{C}(t)$ and ![]() $f_{C,\ell^\infty}(t)$:
$f_{C,\ell^\infty}(t)$:
Theorem 1.7. (Grothendieck–Lefschetz formula, [Reference Deligne17])
The equality ![]() $P_{C}(t)=t^{2g} f_{C, \ell^\infty}(1/t)$ holds for every prime
$P_{C}(t)=t^{2g} f_{C, \ell^\infty}(1/t)$ holds for every prime ![]() $\ell \neq p$. In particular, the polynomial
$\ell \neq p$. In particular, the polynomial ![]() $f_{C, \ell^\infty}(t)\in\mathbb{Z}_\ell[t]$ has integer coefficients and does not depend on
$f_{C, \ell^\infty}(t)\in\mathbb{Z}_\ell[t]$ has integer coefficients and does not depend on ![]() $\ell$.
$\ell$.
2. The distribution of L-polynomials modulo an integer N
In this section, we adapt [Reference Katz and Sarnak29, § 10] to the problem of the distribution of characteristic polynomials of Frobenius modulo a fixed integer ![]() $N \geq 2$ (as opposed to the distribution of the coefficients with respect to the Archimedean metric which is considered in [Reference Katz and Sarnak29]). Fix a genus
$N \geq 2$ (as opposed to the distribution of the coefficients with respect to the Archimedean metric which is considered in [Reference Katz and Sarnak29]). Fix a genus ![]() $g \geq 2$ and a finite field
$g \geq 2$ and a finite field ![]() $\mathbb{F}_q$ of characteristic p > 0 (not dividing N). We denote by
$\mathbb{F}_q$ of characteristic p > 0 (not dividing N). We denote by ![]() $\mathcal{M}_g$ the stack of smooth projective curves of genus g, so that
$\mathcal{M}_g$ the stack of smooth projective curves of genus g, so that ![]() $\mathcal{M}_g(\mathbb{F}_q)$ denotes the set of
$\mathcal{M}_g(\mathbb{F}_q)$ denotes the set of ![]() $\mathbb{F}_q$-isomorphism classes of smooth projective curves of genus g over
$\mathbb{F}_q$-isomorphism classes of smooth projective curves of genus g over ![]() $\mathbb{F}_q$. We see
$\mathbb{F}_q$. We see ![]() $\mathcal{M}_g(\mathbb{F}_q)$ as a probability space by endowing it with one of the following two natural measures:
$\mathcal{M}_g(\mathbb{F}_q)$ as a probability space by endowing it with one of the following two natural measures:
• the ‘naive’ counting measure
 $\mathbb{P}^{\operatorname{naive}}_{g, q}$, which assigns equal measure to every singleton
$\mathbb{P}^{\operatorname{naive}}_{g, q}$, which assigns equal measure to every singleton  $\{C\}$, and which we normalize by requiring
$\{C\}$, and which we normalize by requiring  $\mathbb{P}^{\operatorname{naive}}_{g, q}(\mathcal{M}_g(\mathbb{F}_q))=1$.
$\mathbb{P}^{\operatorname{naive}}_{g, q}(\mathcal{M}_g(\mathbb{F}_q))=1$.• the ‘intrinsic’ measure
 $\mathbb{P}^{\operatorname{intr}}_{g, q}$ such that
$\mathbb{P}^{\operatorname{intr}}_{g, q}$ such that
 \begin{equation*}
\mathbb{P}^{\operatorname{intr}}_{g, q}(\{C\}) = \alpha \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})},
\end{equation*}
\begin{equation*}
\mathbb{P}^{\operatorname{intr}}_{g, q}(\{C\}) = \alpha \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})},
\end{equation*}where
 $\operatorname{Aut}(C_{\mathbb{F}_q})$ is the group of automorphisms of C defined over
$\operatorname{Aut}(C_{\mathbb{F}_q})$ is the group of automorphisms of C defined over  $\mathbb{F}_q$ and
$\mathbb{F}_q$ and
 \begin{equation*}
\alpha = \left(\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \frac{1}{\# \operatorname{Aut}(C_{\mathbb{F}_q})}\right)^{-1}
\end{equation*}
\begin{equation*}
\alpha = \left(\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \frac{1}{\# \operatorname{Aut}(C_{\mathbb{F}_q})}\right)^{-1}
\end{equation*}is the uniquely determined normalization constant that ensures
 \begin{equation*}\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C\})=\mathbb{P}^{\operatorname{intr}}_{g, q}(\mathcal{M}_g(\mathbb{F}_q))=1.\end{equation*}
\begin{equation*}\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C\})=\mathbb{P}^{\operatorname{intr}}_{g, q}(\mathcal{M}_g(\mathbb{F}_q))=1.\end{equation*}Note that α is simply the inverse of the (groupoid) cardinality of
 $\mathcal{M}_g(\mathbb{F}_q)$. In other words, it is the inverse of the number of points of the moduli space of curves of genus g over
$\mathcal{M}_g(\mathbb{F}_q)$. In other words, it is the inverse of the number of points of the moduli space of curves of genus g over  $\mathbb{F}_q$, when these are counted with the correct weight (given by the inverse of the size of their automorphism group).
$\mathbb{F}_q$, when these are counted with the correct weight (given by the inverse of the size of their automorphism group).
Our objective in this section is to study the random variable
 \begin{align*}
\begin{array}{cccc}
\operatorname{charpol} : &\mathcal{M}_g(\mathbb{F}_q) & \to & \mathbb{Z}[t] \\
& C & \mapsto & f_{C, \ell^\infty}(t),
\end{array}
\end{align*}
\begin{align*}
\begin{array}{cccc}
\operatorname{charpol} : &\mathcal{M}_g(\mathbb{F}_q) & \to & \mathbb{Z}[t] \\
& C & \mapsto & f_{C, \ell^\infty}(t),
\end{array}
\end{align*} where ![]() $\ell$ is any auxiliary prime different from p that we use to compute the characteristic polynomial of the Frobenius acting on
$\ell$ is any auxiliary prime different from p that we use to compute the characteristic polynomial of the Frobenius acting on ![]() $\operatorname{Jac}(C)$. More precisely, we will consider the (infinitely many) random variables
$\operatorname{Jac}(C)$. More precisely, we will consider the (infinitely many) random variables
 \begin{equation*}
\begin{array}{cccc}
\operatorname{charpol}_N : &\mathcal{M}_g(\mathbb{F}_q) & \to & \mathbb{Z}/N\mathbb{Z}[t] \\
& C & \mapsto & f_{C, \ell^\infty}(t) \bmod N
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{cccc}
\operatorname{charpol}_N : &\mathcal{M}_g(\mathbb{F}_q) & \to & \mathbb{Z}/N\mathbb{Z}[t] \\
& C & \mapsto & f_{C, \ell^\infty}(t) \bmod N
\end{array}
\end{equation*} obtained from ![]() $\operatorname{charpol}$ by reducing the characteristic polynomials modulo N, for all
$\operatorname{charpol}$ by reducing the characteristic polynomials modulo N, for all ![]() $N \not \equiv 0 (\mathrm{mod}\ p)$. For simplicity, since
$N \not \equiv 0 (\mathrm{mod}\ p)$. For simplicity, since ![]() $\operatorname{charpol}(C)$ is always a monic polynomial of degree 2g, we restrict the codomain to be the finite set
$\operatorname{charpol}(C)$ is always a monic polynomial of degree 2g, we restrict the codomain to be the finite set ![]() $\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$, the additive group of polynomials with coefficients in
$\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$, the additive group of polynomials with coefficients in ![]() $\mathbb{Z}/N\mathbb{Z}$ and degree at most 2g. For each positive integer N not divisible by p, we obtain a measure
$\mathbb{Z}/N\mathbb{Z}$ and degree at most 2g. For each positive integer N not divisible by p, we obtain a measure ![]() $\mu_N^q$ on
$\mu_N^q$ on ![]() $\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$ as follows. Consider the finite set
$\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$ as follows. Consider the finite set  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ and its natural counting measure
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ and its natural counting measure  $\mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}$, normalized so that the total mass is 1. Concretely, this is given by
$\mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}$, normalized so that the total mass is 1. Concretely, this is given by
 \begin{equation*}
\mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}(X) = \frac{\#X}{\#\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})} \quad\quad \forall X \subseteq \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}).
\end{equation*}
\begin{equation*}
\mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}(X) = \frac{\#X}{\#\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})} \quad\quad \forall X \subseteq \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}).
\end{equation*}The map
 \begin{equation*}
\operatorname{charpol} : \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) \to \mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}
\end{equation*}
\begin{equation*}
\operatorname{charpol} : \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) \to \mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}
\end{equation*} that sends each matrix in  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ to its characteristic polynomial allows us to define the measure
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ to its characteristic polynomial allows us to define the measure
 \begin{equation*}
\mu_N^q := (\operatorname{charpol})_* \mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}.
\end{equation*}
\begin{equation*}
\mu_N^q := (\operatorname{charpol})_* \mu_{\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})}.
\end{equation*}We will show:
Theorem 2.1. Let ![]() $N, g$ be positive integers with
$N, g$ be positive integers with ![]() $g \geq 2$. With the notation above, as
$g \geq 2$. With the notation above, as ![]() $q \to \infty$ along prime powers with
$q \to \infty$ along prime powers with ![]() $(q, N)=1$, the measures
$(q, N)=1$, the measures  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q}-\mu_N^q$ and
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q}-\mu_N^q$ and  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$ converge weakly to 0.
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$ converge weakly to 0.
Remark 2.2. For g = 1, very precise results about the distribution of characteristic polynomials modulo arbitrary integers N are proven in [Reference Castryck and Hubrechts13]. In particular, the results of that article describe a very explicit measure ![]() $\tilde{\mu}_N^q$ and show that for g = 1 the difference
$\tilde{\mu}_N^q$ and show that for g = 1 the difference  $(\operatorname{charpol}_N)_* \mathbb{P}_{1,g}^{\operatorname{naive}}-\tilde{\mu}_N^q$ converges to zero with an error of size at most
$(\operatorname{charpol}_N)_* \mathbb{P}_{1,g}^{\operatorname{naive}}-\tilde{\mu}_N^q$ converges to zero with an error of size at most ![]() $O_N(q^{-1/2})$. Thus, the case g = 1 is very well understood. For this reason, and since theorem 2.4 below does not apply in genus 1, we exclude the case g = 1 from our discussion.
$O_N(q^{-1/2})$. Thus, the case g = 1 is very well understood. For this reason, and since theorem 2.4 below does not apply in genus 1, we exclude the case g = 1 from our discussion.
We begin by recalling a version of Deligne’s equidistribution theorem, as extended by Katz and Katz–Sarnak. We partially follow the presentation in [Reference Achter and Holden6, § 2]. We fix an integer ![]() $N \geq 2$ and a geometrically connected, smooth, finite-type
$N \geq 2$ and a geometrically connected, smooth, finite-type ![]() $\mathbb{Z}[1/N]$-scheme U whose fibres are all geometrically connected of the same dimension. Denote by η the generic point of U and by
$\mathbb{Z}[1/N]$-scheme U whose fibres are all geometrically connected of the same dimension. Denote by η the generic point of U and by ![]() $\overline{\eta}$ a corresponding geometric generic point. Let
$\overline{\eta}$ a corresponding geometric generic point. Let ![]() $\mathcal{F}$ be a local system of symplectic free
$\mathcal{F}$ be a local system of symplectic free ![]() $\mathbb{Z}/N\mathbb{Z}$-modules of rank 2g on U—equivalently, a representation
$\mathbb{Z}/N\mathbb{Z}$-modules of rank 2g on U—equivalently, a representation
Given a finite field k of characteristic not dividing N, there is a unique map ![]() $\operatorname{Spec} k \to \operatorname{Spec} \mathbb{Z}[1/N]$. As in the introduction, a classical construction associates with every
$\operatorname{Spec} k \to \operatorname{Spec} \mathbb{Z}[1/N]$. As in the introduction, a classical construction associates with every ![]() $u \in U(k)$ a (conjugacy class of) Frobenius
$u \in U(k)$ a (conjugacy class of) Frobenius ![]() $\operatorname{Frob}_{u, k} \in \pi_1(U, \overline{\eta})$.
$\operatorname{Frob}_{u, k} \in \pi_1(U, \overline{\eta})$.
Theorem 2.3. In the situation above, suppose that the following holds. For every finite field k (of characteristic not dividing N) and for the unique map
![]() $\operatorname{Spec} k \to \operatorname{Spec} \mathbb{Z}[1/N]$, denote by
$\operatorname{Spec} k \to \operatorname{Spec} \mathbb{Z}[1/N]$, denote by ![]() $\overline{\eta}_k$ a geometric generic point of Uk and write
$\overline{\eta}_k$ a geometric generic point of Uk and write ![]() $\pi_1^{\operatorname{geom}}(U_k,\overline{\eta}_k) = \pi_1\left( U_{\overline{k}}, \overline{\eta}_k \right)$. The representation
$\pi_1^{\operatorname{geom}}(U_k,\overline{\eta}_k) = \pi_1\left( U_{\overline{k}}, \overline{\eta}_k \right)$. The representation ![]() $\rho_{\mathcal{F}}$ fits in a commutative diagram
$\rho_{\mathcal{F}}$ fits in a commutative diagram

where ![]() $\rho_\mathcal{F}^{\operatorname{geom}}$ is surjective and
$\rho_\mathcal{F}^{\operatorname{geom}}$ is surjective and ![]() $\rho_{\mathcal{F}}^k$ sends the canonical generator
$\rho_{\mathcal{F}}^k$ sends the canonical generator ![]() $\operatorname{Frob}_k$ of
$\operatorname{Frob}_k$ of ![]() $\operatorname{Gal}\left( \overline{k}/ k \right)$ to
$\operatorname{Gal}\left( \overline{k}/ k \right)$ to ![]() $\#k$. Suppose furthermore that the restriction of
$\#k$. Suppose furthermore that the restriction of ![]() $\rho_{\mathcal{F}}$ to
$\rho_{\mathcal{F}}$ to  $\pi_1(U_{\overline{\mathbb{Q}}}, \overline{\eta})$ has image in
$\pi_1(U_{\overline{\mathbb{Q}}}, \overline{\eta})$ has image in ![]() $\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$.
$\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$.
There is a constant C (depending at most on U, ![]() $\mathcal{F}$, and N) such that, for any union of conjugacy classes
$\mathcal{F}$, and N) such that, for any union of conjugacy classes ![]() $W\subseteq \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ and any finite field k of characteristic not dividing N, we have
$W\subseteq \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ and any finite field k of characteristic not dividing N, we have
 \begin{equation*}
\left|
\frac{
\# \left\{u \in U(k) : \rho_\mathcal{F}(\operatorname{Frob}_{u,k}) \in W \right\} }
{\#U(k)}
-
\frac{\#(W\cap \operatorname{GSp}_{2g}^{\gamma(k)}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})} \right|
\le
\frac C{\sqrt{\#k}},
\end{equation*}
\begin{equation*}
\left|
\frac{
\# \left\{u \in U(k) : \rho_\mathcal{F}(\operatorname{Frob}_{u,k}) \in W \right\} }
{\#U(k)}
-
\frac{\#(W\cap \operatorname{GSp}_{2g}^{\gamma(k)}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})} \right|
\le
\frac C{\sqrt{\#k}},
\end{equation*} where ![]() $\gamma(k)=\# k$ is the image of the canonical generator of
$\gamma(k)=\# k$ is the image of the canonical generator of ![]() $\operatorname{Gal}(\overline{k}/k)$ under
$\operatorname{Gal}(\overline{k}/k)$ under ![]() $\rho_{\mathcal{F}}^{k}$.
$\rho_{\mathcal{F}}^{k}$.
The deduction of this result from the work of Katz–Sarnak [Reference Katz and Sarnak29] is certainly well known to experts, but it is difficult to find details in print: see for example [Reference Castryck, Folsom, Hubrechts and Sutherland12, principle 2], where a similar result is labelled Principle ‘because no complete proof of this statement has appeared in the literature to date’. We thus prefer to provide a short proof.
Proof. This is a special case of [Reference Katz and Sarnak29, theorem 9.7.13]. More precisely, we fix an auxiliary prime ![]() $\ell$ dividing N and a faithful
$\ell$ dividing N and a faithful ![]() $\overline{\mathbb{Q}_\ell}$-representation
$\overline{\mathbb{Q}_\ell}$-representation ![]() $\Lambda : \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z}) \to \operatorname{GL}(V)$ for some
$\Lambda : \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z}) \to \operatorname{GL}(V)$ for some ![]() $\overline{\mathbb{Q}_\ell}$-vector space V, and apply [Reference Katz and Sarnak29, theorem 9.7.13] to the
$\overline{\mathbb{Q}_\ell}$-vector space V, and apply [Reference Katz and Sarnak29, theorem 9.7.13] to the ![]() $\ell$-adic sheaf
$\ell$-adic sheaf ![]() $\mathcal{F}^{\prime}$ corresponding to the representation
$\mathcal{F}^{\prime}$ corresponding to the representation ![]() $\rho := \Lambda \circ \rho_{\mathcal{F}}$. In the notation of [Reference Katz and Sarnak29, § 9.7.1], we further take
$\rho := \Lambda \circ \rho_{\mathcal{F}}$. In the notation of [Reference Katz and Sarnak29, § 9.7.1], we further take ![]() $S=\operatorname{Spec} \mathbb{Z}[1/N]$ and X = U.
$S=\operatorname{Spec} \mathbb{Z}[1/N]$ and X = U.
We check that these data satisfy assumptions (1)–(4) of [Reference Katz and Sarnak29, § 9.7.2]; set ![]() $G_{\operatorname{arith}} = \Lambda(\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})) \cong \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ and
$G_{\operatorname{arith}} = \Lambda(\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})) \cong \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ and ![]() $G = \Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})) \cong \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ (we identify these finite groups with constant algebraic subgroups of
$G = \Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})) \cong \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ (we identify these finite groups with constant algebraic subgroups of ![]() $\operatorname{GL}(V)$).
$\operatorname{GL}(V)$).
1. The fact that
 $\rho(\pi_1(U, \overline{\eta})) \subset G_{\operatorname{arith}}(\overline{\mathbb{Q}_\ell})$ is true by definition. The Zariski density of
$\rho(\pi_1(U, \overline{\eta})) \subset G_{\operatorname{arith}}(\overline{\mathbb{Q}_\ell})$ is true by definition. The Zariski density of  $\rho(\pi_1(U, \overline{\eta}))$ in
$\rho(\pi_1(U, \overline{\eta}))$ in  $G_{\operatorname{arith}}(\overline{\mathbb{Q}_\ell})$ is equivalent to the fact that
$G_{\operatorname{arith}}(\overline{\mathbb{Q}_\ell})$ is equivalent to the fact that  $\Lambda \circ \rho_{\mathcal{F}}$ surjects onto
$\Lambda \circ \rho_{\mathcal{F}}$ surjects onto  $G_{\operatorname{arith}}$, or equivalently, that
$G_{\operatorname{arith}}$, or equivalently, that  $\rho_{\mathcal{F}}$ surjects onto
$\rho_{\mathcal{F}}$ surjects onto  $\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$. The image of
$\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$. The image of  $\rho_{\mathcal{F}}$ contains the image of
$\rho_{\mathcal{F}}$ contains the image of  $\rho_{\mathcal{F}}^{\operatorname{geom}}$ (for any finite field k of characteristic prime to N), which is
$\rho_{\mathcal{F}}^{\operatorname{geom}}$ (for any finite field k of characteristic prime to N), which is  $\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ by assumption. On the other hand, by the commutative diagram in the statement, the image of
$\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ by assumption. On the other hand, by the commutative diagram in the statement, the image of  $\operatorname{mult} \circ \rho_{\mathcal{F}}$ contains
$\operatorname{mult} \circ \rho_{\mathcal{F}}$ contains  $\rho_{\mathcal{F}}^k(\operatorname{Frob}_k)=\#k$ for any finite field k of characteristic prime to N. By Dirichlet’s theorem, the quantity
$\rho_{\mathcal{F}}^k(\operatorname{Frob}_k)=\#k$ for any finite field k of characteristic prime to N. By Dirichlet’s theorem, the quantity  $\#k$ realizes all invertible classes modulo N, hence the image of
$\#k$ realizes all invertible classes modulo N, hence the image of  $\operatorname{mult} \circ \rho_{\mathcal{F}}$ contains all of
$\operatorname{mult} \circ \rho_{\mathcal{F}}$ contains all of  $(\mathbb{Z}/N\mathbb{Z})^\times$. Taken together, these facts imply that the image of
$(\mathbb{Z}/N\mathbb{Z})^\times$. Taken together, these facts imply that the image of  $\rho_{\mathcal{F}}$ is
$\rho_{\mathcal{F}}$ is  $\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$.
$\operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$.2. The inclusion
 $\rho(\pi(U_{\overline{\mathbb{Q}}}, \overline{\eta})) \subseteq \Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z}))$ is true by assumption.
$\rho(\pi(U_{\overline{\mathbb{Q}}}, \overline{\eta})) \subseteq \Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z}))$ is true by assumption.3. We have to check that for every finite field k and every k-valued point s of
 $\mathbb{Z}[1/N]$, the geometric monodromy group of
$\mathbb{Z}[1/N]$, the geometric monodromy group of  $\mathcal{F}|_{U_s}$ is
$\mathcal{F}|_{U_s}$ is  $\Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z}))$. This is precisely the assumption that
$\Lambda(\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z}))$. This is precisely the assumption that  $\rho_{\mathcal{F}}^{\operatorname{geom}}$ is surjective for every finite field k.
$\rho_{\mathcal{F}}^{\operatorname{geom}}$ is surjective for every finite field k.4. The image of Λ is finite. Thus, all eigenvalues of any matrix in its image are roots of unity. This implies that
 $\mathcal{F}$ is ι-pure of weight 0, for any embedding ι of
$\mathcal{F}$ is ι-pure of weight 0, for any embedding ι of  $\overline{\mathbb{Q}_\ell}$ into
$\overline{\mathbb{Q}_\ell}$ into  $\mathbb{C}$. See also the proof of [Reference Chavdarov15, theorem 4.1].
$\mathbb{C}$. See also the proof of [Reference Chavdarov15, theorem 4.1].
Since ![]() $G_{\operatorname{arith}}$ is a finite group (which implies that
$G_{\operatorname{arith}}$ is a finite group (which implies that ![]() $K_{\operatorname{arith}}=G_{\operatorname{arith}}$ is finite, in the notation of [Reference Katz and Sarnak29, theorem 9.7.13], see [Reference Katz and Sarnak29, remark 9.7.11]), the conclusion follows from [Reference Katz and Sarnak29, theorem 9.7.13]. Note that here we also use the obvious fact that
$K_{\operatorname{arith}}=G_{\operatorname{arith}}$ is finite, in the notation of [Reference Katz and Sarnak29, theorem 9.7.13], see [Reference Katz and Sarnak29, remark 9.7.11]), the conclusion follows from [Reference Katz and Sarnak29, theorem 9.7.13]. Note that here we also use the obvious fact that  $\#\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) = \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ for any q prime to N.
$\#\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) = \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ for any q prime to N.
Let ![]() $\mathcal{C} \xrightarrow{\pi} U \to \operatorname{Spec} \mathbb{Z}[1/N]$ be a smooth, irreducible family of projective curves of genus
$\mathcal{C} \xrightarrow{\pi} U \to \operatorname{Spec} \mathbb{Z}[1/N]$ be a smooth, irreducible family of projective curves of genus ![]() $g \ge 1$, with the property that the map
$g \ge 1$, with the property that the map ![]() $U \to \operatorname{Spec} \mathbb{Z}[1/N]$ has geometrically irreducible fibres, all of the same dimension. The étale sheaf
$U \to \operatorname{Spec} \mathbb{Z}[1/N]$ has geometrically irreducible fibres, all of the same dimension. The étale sheaf ![]() $\mathcal{F} = \mathcal{F}_{\mathcal{C},N} := \operatorname{Jac}(\mathcal{C})[N]$ is a sheaf of
$\mathcal{F} = \mathcal{F}_{\mathcal{C},N} := \operatorname{Jac}(\mathcal{C})[N]$ is a sheaf of ![]() $\mathbb{Z}/N\mathbb{Z}$-free symplectic modules of rank 2g whose fibre at a geometric point
$\mathbb{Z}/N\mathbb{Z}$-free symplectic modules of rank 2g whose fibre at a geometric point ![]() $\overline{x}\in
U$ is the N-torsion of the Jacobian
$\overline{x}\in
U$ is the N-torsion of the Jacobian ![]() $\operatorname{Jac}(\mathcal{C}_x)[N]$. Theorem 2.3 applies to this situation provided that
$\operatorname{Jac}(\mathcal{C}_x)[N]$. Theorem 2.3 applies to this situation provided that ![]() $\rho_{\mathcal{F}}^{\operatorname{geom}}$ is surjective for every finite field k of characteristic not dividing N. The existence of a commutative diagram as in (1) is automatic thanks to well-known properties of the Weil pairing. The assumption
$\rho_{\mathcal{F}}^{\operatorname{geom}}$ is surjective for every finite field k of characteristic not dividing N. The existence of a commutative diagram as in (1) is automatic thanks to well-known properties of the Weil pairing. The assumption  $\rho_{\mathcal{F}}(\pi_1(U_{\overline{\mathbb{Q}}}, \overline{\eta})) \subseteq \operatorname{Sp}(\mathcal{F}_{\overline{\eta}})$ is also automatically satisfied, again by the properties of the Weil pairing. We will say that the family of curves
$\rho_{\mathcal{F}}(\pi_1(U_{\overline{\mathbb{Q}}}, \overline{\eta})) \subseteq \operatorname{Sp}(\mathcal{F}_{\overline{\eta}})$ is also automatically satisfied, again by the properties of the Weil pairing. We will say that the family of curves ![]() $\mathcal{C} \to U$ has full N-monodromy if the associated representation
$\mathcal{C} \to U$ has full N-monodromy if the associated representation  $\rho_\mathcal{F}: \pi_1^{\operatorname{geom}}(U_k, \overline{\eta}_k)
\to \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ is surjective for every finite field k of characteristic not dividing N.
$\rho_\mathcal{F}: \pi_1^{\operatorname{geom}}(U_k, \overline{\eta}_k)
\to \operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})$ is surjective for every finite field k of characteristic not dividing N.
For the proof of theorem 2.1, we will rely on the functor ![]() $\mathcal{M}_{g, 3K}$ of tri-canonically embedded curves. Referring the reader to [Reference Katz and Sarnak29, § 10.6] and [Reference Deligne and Mumford19] for more details, we recall that for a field k one has
$\mathcal{M}_{g, 3K}$ of tri-canonically embedded curves. Referring the reader to [Reference Katz and Sarnak29, § 10.6] and [Reference Deligne and Mumford19] for more details, we recall that for a field k one has
 \begin{equation*}
\mathcal{M}_{g, 3K}(k) = \left\{(C/k, \alpha) :
\begin{array}{c} C/k \,\text{is a smooth projective} \\ \text{curve of genus}\ g \\ \alpha \,\text{is a basis of } H^0\left(C, (\Omega^1_{C/k})^{\otimes 3}\right) \end{array} \right\} / k\text{-isomorphism}.
\end{equation*}
\begin{equation*}
\mathcal{M}_{g, 3K}(k) = \left\{(C/k, \alpha) :
\begin{array}{c} C/k \,\text{is a smooth projective} \\ \text{curve of genus}\ g \\ \alpha \,\text{is a basis of } H^0\left(C, (\Omega^1_{C/k})^{\otimes 3}\right) \end{array} \right\} / k\text{-isomorphism}.
\end{equation*} The functor ![]() $\mathcal{M}_{g, 3K}$ was extensively studied by Mumford [Reference Mumford43] and Deligne–Mumford [Reference Deligne and Mumford19]. We will need the following results:
$\mathcal{M}_{g, 3K}$ was extensively studied by Mumford [Reference Mumford43] and Deligne–Mumford [Reference Deligne and Mumford19]. We will need the following results:
Theorem 2.4. Deligne–Mumford [Reference Deligne and Mumford19, § 5], see also [Reference Katz and Sarnak29, Theorem 10.6.10]
Let ![]() $g\geq 2$. The following hold:
$g\geq 2$. The following hold:
1. The functor
 $\mathcal{M}_{g, 3K}$ is represented by a smooth
$\mathcal{M}_{g, 3K}$ is represented by a smooth  $\mathbb{Z}$-scheme of relative dimension
$\mathbb{Z}$-scheme of relative dimension  $3g-3+(5g-5)^2$, with geometrically connected fibres.
$3g-3+(5g-5)^2$, with geometrically connected fibres.2.
 $\mathcal{M}_{g, 3K}$ is a fine moduli space: there exists a universal curve
$\mathcal{M}_{g, 3K}$ is a fine moduli space: there exists a universal curve  $\mathcal{C}_{g, 3K} \to \mathcal{M}_{g, 3K}$.
$\mathcal{C}_{g, 3K} \to \mathcal{M}_{g, 3K}$.
There is an obvious forgetful functor ![]() $
\mathcal{M}_{g, 3K} \to \mathcal{M}_{g},
$ which on field-valued points is given by
$
\mathcal{M}_{g, 3K} \to \mathcal{M}_{g},
$ which on field-valued points is given by
 \begin{equation*}
\begin{array}{ccc}
\mathcal{M}_{g, 3K}(k) & \to & \mathcal{M}_{g}(k) \\
(C/k, \alpha) & \mapsto & C/k.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
\mathcal{M}_{g, 3K}(k) & \to & \mathcal{M}_{g}(k) \\
(C/k, \alpha) & \mapsto & C/k.
\end{array}
\end{equation*} This map is surjective for every field k, and, when k is finite, the fibre over any ![]() $C/k \in \mathcal{M}_g(k)$ has cardinality
$C/k \in \mathcal{M}_g(k)$ has cardinality  $\displaystyle \frac{\#\operatorname{GL}_{5g-5}(k)}{\#\operatorname{Aut}(C/k)}$ [Reference Katz and Sarnak29, lemma 10.6.8]. As an immediate consequence [Reference Katz and Sarnak29, lemma 10.7.8], the intrinsic measure
$\displaystyle \frac{\#\operatorname{GL}_{5g-5}(k)}{\#\operatorname{Aut}(C/k)}$ [Reference Katz and Sarnak29, lemma 10.6.8]. As an immediate consequence [Reference Katz and Sarnak29, lemma 10.7.8], the intrinsic measure  $\mathbb{P}^{\operatorname{intr}}_{g, q}$ on
$\mathbb{P}^{\operatorname{intr}}_{g, q}$ on ![]() $\mathcal{M}_{g}(\mathbb{F}_q)$ can be described as
$\mathcal{M}_{g}(\mathbb{F}_q)$ can be described as
 \begin{equation}
\frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_C,
\end{equation}
\begin{equation}
\frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_C,
\end{equation} where δC is the characteristic function of the singleton ![]() $\{C\}$. By theorem 2.4 (2), we have that the sum
$\{C\}$. By theorem 2.4 (2), we have that the sum  $\sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_C$ can be replaced by
$\sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_C$ can be replaced by
 \begin{equation}
\sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_{(\mathcal{C}_{g, 3K})_u},
\end{equation}
\begin{equation}
\sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \delta_{(\mathcal{C}_{g, 3K})_u},
\end{equation} where ![]() $(\mathcal{C}_{g, 3K})_u$ is the fibre over
$(\mathcal{C}_{g, 3K})_u$ is the fibre over ![]() $u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)$ of the universal curve
$u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)$ of the universal curve ![]() $\mathcal{C}_{g, 3K} \to \mathcal{M}_{g, 3K}$. We will apply theorem 2.3 to
$\mathcal{C}_{g, 3K} \to \mathcal{M}_{g, 3K}$. We will apply theorem 2.3 to  $U=\left(\mathcal{M}_{g, 3K}\right)_{\mathbb{Z}[1/N]}$ and
$U=\left(\mathcal{M}_{g, 3K}\right)_{\mathbb{Z}[1/N]}$ and  $\mathcal{F} = \mathcal{F}_{\mathcal{C}_{g, 3K}, N}$. For
$\mathcal{F} = \mathcal{F}_{\mathcal{C}_{g, 3K}, N}$. For ![]() $g \geq 2$ and
$g \geq 2$ and ![]() $p \nmid N$, this family has full N-monodromy by [Reference Deligne and Mumford19, 5.12] (see also the discussion in [Reference Landesman, Swaminathan, Tao and Xu35, § 5]). We are almost ready to prove theorem 2.1, but before doing so, we need a few estimates on the size of
$p \nmid N$, this family has full N-monodromy by [Reference Deligne and Mumford19, 5.12] (see also the discussion in [Reference Landesman, Swaminathan, Tao and Xu35, § 5]). We are almost ready to prove theorem 2.1, but before doing so, we need a few estimates on the size of ![]() $\mathcal{M}_g(\mathbb{F}_q)$:
$\mathcal{M}_g(\mathbb{F}_q)$:
Lemma 2.5. For every ![]() $g \geq 3$, the following hold:
$g \geq 3$, the following hold:
1.
 $\#\mathcal{M}_g(\mathbb{F}_q) = \sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} 1 = q^{3g-3}(1+O_g(q^{-1/2}))$;
$\#\mathcal{M}_g(\mathbb{F}_q) = \sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} 1 = q^{3g-3}(1+O_g(q^{-1/2}))$;2.
 $\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})} = q^{3g-3}(1+O_g(q^{-1/2}))$;
$\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})} = q^{3g-3}(1+O_g(q^{-1/2}))$;3.
 $\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \geq 2 \right\} = O_g(q^{3g-3-1})$.
$\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \geq 2 \right\} = O_g(q^{3g-3-1})$.
For g = 2, one has
1ʹ.
 $\#\mathcal{M}_2(\mathbb{F}_q) = \sum_{C \in \mathcal{M}_2(\mathbb{F}_q)} 1 = q^{3}(1+O(q^{-1/2}))$;
$\#\mathcal{M}_2(\mathbb{F}_q) = \sum_{C \in \mathcal{M}_2(\mathbb{F}_q)} 1 = q^{3}(1+O(q^{-1/2}))$;2ʹ.
 $\sum_{C \in \mathcal{M}_2(\mathbb{F}_q)} \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})} = \frac{1}{2}q^{3}(1+O(q^{-1/2}))$;
$\sum_{C \in \mathcal{M}_2(\mathbb{F}_q)} \frac{1}{\#\operatorname{Aut}(C_{\mathbb{F}_q})} = \frac{1}{2}q^{3}(1+O(q^{-1/2}))$;3ʹ.
 $\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \gt 2 \right\} = O(q^{2})$.
$\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \gt 2 \right\} = O(q^{2})$.
Proof. For ![]() $g \geq 3$, all the statements follow from [Reference Katz and Sarnak29, lemmas 10.6.23, 10.6.25, and 10.6.26], together with the obvious asymptotic relation
$g \geq 3$, all the statements follow from [Reference Katz and Sarnak29, lemmas 10.6.23, 10.6.25, and 10.6.26], together with the obvious asymptotic relation  $\#\operatorname{GL}_{5g-5}(\mathbb{F}_q) \sim q^{(5g-5)^2}(1+O_g(q^{-1}))$. For g = 2, one can adapt the proof of the same lemmas in [Reference Katz and Sarnak29], simply taking into account that the open subset
$\#\operatorname{GL}_{5g-5}(\mathbb{F}_q) \sim q^{(5g-5)^2}(1+O_g(q^{-1}))$. For g = 2, one can adapt the proof of the same lemmas in [Reference Katz and Sarnak29], simply taking into account that the open subset ![]() $U_{\leq 2}$ of
$U_{\leq 2}$ of ![]() $\mathcal{M}_{2}$ parametrizing curves whose geometric automorphism group has order 2 meets every geometric fibre of
$\mathcal{M}_{2}$ parametrizing curves whose geometric automorphism group has order 2 meets every geometric fibre of ![]() $\mathcal{M}_{2, 3K}/\mathbb{Z}$ [Reference Katz and Sarnak29, lemma 10.6.13, remark 10.6.20]. In particular, the generic value of
$\mathcal{M}_{2, 3K}/\mathbb{Z}$ [Reference Katz and Sarnak29, lemma 10.6.13, remark 10.6.20]. In particular, the generic value of ![]() $\#\operatorname{Aut}(C_{\mathbb{F}_q})$ for (smooth projective) curves of genus 2 is 2. Note that when the group
$\#\operatorname{Aut}(C_{\mathbb{F}_q})$ for (smooth projective) curves of genus 2 is 2. Note that when the group ![]() $\operatorname{Aut}(C_{\mathbb{F}_q})$ has order 2 it is generated by the hyperelliptic involution.
$\operatorname{Aut}(C_{\mathbb{F}_q})$ has order 2 it is generated by the hyperelliptic involution.
Corollary 2.6. For all ![]() $g \geq 2$, we have
$g \geq 2$, we have  $\displaystyle
\sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) - \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\}) \right| = O_g(q^{-1/2}).
$
$\displaystyle
\sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) - \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\}) \right| = O_g(q^{-1/2}).
$
Proof. For ![]() $g \geq 3$, using the definition of
$g \geq 3$, using the definition of  $\mathbb{P}^{\operatorname{naive}}_{g, q}$ and
$\mathbb{P}^{\operatorname{naive}}_{g, q}$ and  $\mathbb{P}^{\operatorname{intr}}_{g, q}$ and lemma 2.5 (1), (2), and (3) we obtain
$\mathbb{P}^{\operatorname{intr}}_{g, q}$ and lemma 2.5 (1), (2), and (3) we obtain
 \begin{equation*}
\begin{aligned}
&\sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) - \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\}) \right|\\ & = \sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \frac{1}{\#\mathcal{M}_g(\mathbb{F}_q)} - \frac{1/\#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})}{\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} 1/\#\operatorname{Aut}(C_{\mathbb{F}_q})} \right| \\
& = \sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| q^{3-3g}(1+O_g(q^{-1/2})) - \frac{q^{3-3g}(1+O_g(q^{-1/2}))}{\#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})}\right| \\
& = \sum_{\substack{C' \in \mathcal{M}_g(\mathbb{F}_q) \\ \#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})=1}} O_g(q^{3-3g-1/2}) + \sum_{\substack{C' \in \mathcal{M}_g(\mathbb{F}_q) \\ \#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q}) \geq 2}} O_g(q^{3-3g}) \\
& = O_g\left( \frac{\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \geq 2 \right\}}{q^{3g-3}} \right) +O_g\left( \frac{\#\mathcal{M}_g(\mathbb{F}_q)}{q^{3g-3}} q^{-1/2} \right) \\
& = O_g(q^{-1}) + O_g(q^{-1/2}) = O_g(q^{-1/2}).
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
&\sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) - \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\}) \right|\\ & = \sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| \frac{1}{\#\mathcal{M}_g(\mathbb{F}_q)} - \frac{1/\#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})}{\sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} 1/\#\operatorname{Aut}(C_{\mathbb{F}_q})} \right| \\
& = \sum_{C' \in \mathcal{M}_g(\mathbb{F}_q)} \left| q^{3-3g}(1+O_g(q^{-1/2})) - \frac{q^{3-3g}(1+O_g(q^{-1/2}))}{\#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})}\right| \\
& = \sum_{\substack{C' \in \mathcal{M}_g(\mathbb{F}_q) \\ \#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q})=1}} O_g(q^{3-3g-1/2}) + \sum_{\substack{C' \in \mathcal{M}_g(\mathbb{F}_q) \\ \#\operatorname{Aut}(C^{\prime}_{\mathbb{F}_q}) \geq 2}} O_g(q^{3-3g}) \\
& = O_g\left( \frac{\#\left\{C \in \mathcal{M}_g(\mathbb{F}_q) : \#\operatorname{Aut}(C_{\overline{\mathbb{F}_q}}) \geq 2 \right\}}{q^{3g-3}} \right) +O_g\left( \frac{\#\mathcal{M}_g(\mathbb{F}_q)}{q^{3g-3}} q^{-1/2} \right) \\
& = O_g(q^{-1}) + O_g(q^{-1/2}) = O_g(q^{-1/2}).
\end{aligned}
\end{equation*}The same proof applies, with minimal changes, also to g = 2, simply using (1’), (2’), and (3’) of lemma 2.5 instead of (1), (2), and (3).
Proof of theorem 2.1
By definition, the weak convergence in the statement means that—for every continuous bounded function f on ![]() $\mathbb{Z}/N\mathbb{Z}[x]_{\leq 2g}$—the integral of f with respect to
$\mathbb{Z}/N\mathbb{Z}[x]_{\leq 2g}$—the integral of f with respect to  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q}-\mu_N^q$ converges to 0 as
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q}-\mu_N^q$ converges to 0 as ![]() $q \to \infty$ and similarly for the sequence of measures
$q \to \infty$ and similarly for the sequence of measures  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$. We begin by treating the case of the measures
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$. We begin by treating the case of the measures  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$. Since any function
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q}-\mu_N^q$. Since any function ![]() $f: \mathbb{Z}/N\mathbb{Z}[x]_{\leq 2g} \to \mathbb{R}$ is a linear combination of characteristic functions of singletons, it suffices to show the result when f is of the form
$f: \mathbb{Z}/N\mathbb{Z}[x]_{\leq 2g} \to \mathbb{R}$ is a linear combination of characteristic functions of singletons, it suffices to show the result when f is of the form
 \begin{equation*}
f(h(t)) = \begin{cases}
1, \text{if }h(t) = h_0(t) \\
0, \text{otherwise}
\end{cases}
\end{equation*}
\begin{equation*}
f(h(t)) = \begin{cases}
1, \text{if }h(t) = h_0(t) \\
0, \text{otherwise}
\end{cases}
\end{equation*} for some polynomial ![]() $h_0(t) \in \mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$. Fix
$h_0(t) \in \mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}$. Fix ![]() $h_0(t)$. The condition
$h_0(t)$. The condition ![]() $\operatorname{charpol}(M) =h_0(t) \in \mathbb{Z}/N\mathbb{Z}[t]$ defines a (possibly empty) union of conjugacy classes
$\operatorname{charpol}(M) =h_0(t) \in \mathbb{Z}/N\mathbb{Z}[t]$ defines a (possibly empty) union of conjugacy classes ![]() $W_{h_0} \subseteq \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$. For a curve
$W_{h_0} \subseteq \operatorname{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})$. For a curve ![]() $C/\mathbb{F}_q$, we denote by
$C/\mathbb{F}_q$, we denote by ![]() $\rho_{C, N}$ the natural representation of
$\rho_{C, N}$ the natural representation of ![]() $\operatorname{Gal}\left(\overline{\mathbb{F}_q}/\mathbb{F}_q \right)$ on the N-torsion of
$\operatorname{Gal}\left(\overline{\mathbb{F}_q}/\mathbb{F}_q \right)$ on the N-torsion of ![]() $\operatorname{Jac}(C)$. We regard
$\operatorname{Jac}(C)$. We regard ![]() $\mathcal{M}_{g, 3K}$ as a
$\mathcal{M}_{g, 3K}$ as a ![]() $\mathbb{Z}[1/N]$-scheme. It will play the role of the scheme U of our general discussion of the Deligne–Katz–Sarnak equidistribution theorem. We take as curve
$\mathbb{Z}[1/N]$-scheme. It will play the role of the scheme U of our general discussion of the Deligne–Katz–Sarnak equidistribution theorem. We take as curve ![]() $\mathcal{C} \to U$ the universal curve
$\mathcal{C} \to U$ the universal curve ![]() $\mathcal{C}_{g, 3K}$ over
$\mathcal{C}_{g, 3K}$ over ![]() $\mathcal{M}_{g, 3K}$.
$\mathcal{M}_{g, 3K}$.
Recall that we introduced the sheaf  $\mathcal{F} = \mathcal{F}_{\mathcal{C}_{g, 3K}, N}$ and that the universal family over
$\mathcal{F} = \mathcal{F}_{\mathcal{C}_{g, 3K}, N}$ and that the universal family over ![]() $\mathcal{M}_{g, 3K}$ has full N-monodromy [Reference Deligne and Mumford19, 5.12]. Given a curve
$\mathcal{M}_{g, 3K}$ has full N-monodromy [Reference Deligne and Mumford19, 5.12]. Given a curve ![]() $\mathcal{C}_u$ in the family
$\mathcal{C}_u$ in the family ![]() $\mathcal{C}$, lying over an
$\mathcal{C}$, lying over an ![]() $\mathbb{F}_q$-rational point u of
$\mathbb{F}_q$-rational point u of ![]() $U = \mathcal{M}_{g, 3K}$, the definitions imply that
$U = \mathcal{M}_{g, 3K}$, the definitions imply that ![]() $\rho_{\mathcal{C}_u, N}(\operatorname{Frob}_q)$ and
$\rho_{\mathcal{C}_u, N}(\operatorname{Frob}_q)$ and ![]() $\rho_{\mathcal{F}}(\operatorname{Frob}_{u, \mathbb{F}_q})$ represent the same conjugacy class.
$\rho_{\mathcal{F}}(\operatorname{Frob}_{u, \mathbb{F}_q})$ represent the same conjugacy class.
For any fixed q, using Eqs. (2) and (3), we have
 \begin{equation}
\begin{aligned}
&\int_{\mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}(C) \bmod N) \, d \mathbb{P}^{\operatorname{intr}}_{g, q}(C)
\\ & \quad = \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} f(\operatorname{charpol}_N(C)) \\
& \quad = \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \mathbf{1}_{{\rho_{\mathcal{C}_u, N}}({\operatorname{Frob}_q}) \in W_{h_0}} \\
& \quad {= \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \mathbf{1}_{\rho_{\mathcal{F}}(\operatorname{Frob}_{u, \mathbb{F}_q}) \in W_{h_0}}} \\
& \quad = \frac{\# \{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q) : {\rho_{\mathcal{F}}}(\operatorname{Frob}_{u,{\mathbb{F}_q}}) \in W_{h_0} \}}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&\int_{\mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}(C) \bmod N) \, d \mathbb{P}^{\operatorname{intr}}_{g, q}(C)
\\ & \quad = \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{(C, \alpha) \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} f(\operatorname{charpol}_N(C)) \\
& \quad = \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \mathbf{1}_{{\rho_{\mathcal{C}_u, N}}({\operatorname{Frob}_q}) \in W_{h_0}} \\
& \quad {= \frac{1}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)} \sum_{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q)} \mathbf{1}_{\rho_{\mathcal{F}}(\operatorname{Frob}_{u, \mathbb{F}_q}) \in W_{h_0}}} \\
& \quad = \frac{\# \{u \in \mathcal{M}_{g, 3K}(\mathbb{F}_q) : {\rho_{\mathcal{F}}}(\operatorname{Frob}_{u,{\mathbb{F}_q}}) \in W_{h_0} \}}{\#\mathcal{M}_{g, 3K}(\mathbb{F}_q)}.
\end{aligned}
\end{equation}We now apply theorem 2.3 to rewrite the above as
 \begin{equation}
\int_{\mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}_N(C) ) \, d \mathbb{P}^{\operatorname{intr}}_{g, q}(C) = \frac{\#\left(W_{h_0} \cap \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) \right)}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})} + O_{g, N}(q^{-1/2}).
\end{equation}
\begin{equation}
\int_{\mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}_N(C) ) \, d \mathbb{P}^{\operatorname{intr}}_{g, q}(C) = \frac{\#\left(W_{h_0} \cap \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z}) \right)}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})} + O_{g, N}(q^{-1/2}).
\end{equation}On the other hand, by definition, we have
 \begin{equation}
\begin{aligned}
\int_{\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}} f(h(t)) \, d\mu_N^q(h) & = \int_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} f(\operatorname{charpol}(M)) \, d\mu_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})}(M) \\
& = \int_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} \mathbf{1}_{\operatorname{charpol}(M) = h_0} \, d\mu_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})}(M) \\
& = \frac{\#(W_{h_0} \cap \operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} \\
& = \frac{\#(W_{h_0} \cap \operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_{\mathbb{Z}/N\mathbb{Z}[t]_{\leq 2g}} f(h(t)) \, d\mu_N^q(h) & = \int_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} f(\operatorname{charpol}(M)) \, d\mu_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})}(M) \\
& = \int_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} \mathbf{1}_{\operatorname{charpol}(M) = h_0} \, d\mu_{\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})}(M) \\
& = \frac{\#(W_{h_0} \cap \operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z})} \\
& = \frac{\#(W_{h_0} \cap \operatorname{GSp}^q_{2g}(\mathbb{Z}/N\mathbb{Z}))}{\#\operatorname{Sp}_{2g}(\mathbb{Z}/N\mathbb{Z})}.
\end{aligned}
\end{equation} The claim follows upon comparing Eqs. (5) and (6). We now show that  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q} - \mu_N^q$ converges weakly to 0. We have already established that
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{naive}}_{g, q} - \mu_N^q$ converges weakly to 0. We have already established that  $(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q} - \mu_N^q$ weakly converges to 0. Thus, it suffices to show that
$(\operatorname{charpol}_N)_* \mathbb{P}^{\operatorname{intr}}_{g, q} - \mu_N^q$ weakly converges to 0. Thus, it suffices to show that  $(\operatorname{charpol}_N)_* (\mathbb{P}^{\operatorname{intr}}_{g, q} - \mathbb{P}^{\operatorname{naive}}_{g, q})$ converges weakly to 0, which in turn is implied by the following statement: for every ɛ > 0, there exists q 0 such that, for all
$(\operatorname{charpol}_N)_* (\mathbb{P}^{\operatorname{intr}}_{g, q} - \mathbb{P}^{\operatorname{naive}}_{g, q})$ converges weakly to 0, which in turn is implied by the following statement: for every ɛ > 0, there exists q 0 such that, for all ![]() $q \gt q_0$ and all subsets A of
$q \gt q_0$ and all subsets A of ![]() $\mathcal{M}_g(\mathbb{F}_q)$, one has
$\mathcal{M}_g(\mathbb{F}_q)$, one has  $|\mathbb{P}^{\operatorname{intr}}_{g, q}(A) - \mathbb{P}^{\operatorname{naive}}_{g, q}(A)| \lt \varepsilon$. This follows immediately from corollary 2.6, because
$|\mathbb{P}^{\operatorname{intr}}_{g, q}(A) - \mathbb{P}^{\operatorname{naive}}_{g, q}(A)| \lt \varepsilon$. This follows immediately from corollary 2.6, because
 \begin{equation*}
\begin{aligned}
|\mathbb{P}^{\operatorname{intr}}_{g, q}(A) - \mathbb{P}^{\operatorname{naive}}_{g, q}(A)| & = \left| \sum_{C' \in A} \left( \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\})-\mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) \right) \right| \\
& \leq \sum_{C' \in A} |\mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\})-\mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\})| = O_g(q^{-1/2}).
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
|\mathbb{P}^{\operatorname{intr}}_{g, q}(A) - \mathbb{P}^{\operatorname{naive}}_{g, q}(A)| & = \left| \sum_{C' \in A} \left( \mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\})-\mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\}) \right) \right| \\
& \leq \sum_{C' \in A} |\mathbb{P}^{\operatorname{intr}}_{g, q}(\{C'\})-\mathbb{P}^{\operatorname{naive}}_{g, q}(\{C'\})| = O_g(q^{-1/2}).
\end{aligned}
\end{equation*}Remark 2.7. Note that the measure ![]() $\mu_N^q$ only depends on
$\mu_N^q$ only depends on ![]() $q \bmod N$. In particular, if we take a sequence of prime powers qi such that
$q \bmod N$. In particular, if we take a sequence of prime powers qi such that ![]() $q_i \bmod N$ is constant (say equal to
$q_i \bmod N$ is constant (say equal to ![]() $r \bmod N$), Theorem 2.1 shows that the measures
$r \bmod N$), Theorem 2.1 shows that the measures  $(\operatorname{charpol}_N)_* \mathbb{P}_{q_i, g}^{\operatorname{intr}}$ converge weakly to
$(\operatorname{charpol}_N)_* \mathbb{P}_{q_i, g}^{\operatorname{intr}}$ converge weakly to ![]() $\mu_N^{r}$. As a special case, taking N = 2, this applies to any choice of qi that are not powers of 2.
$\mu_N^{r}$. As a special case, taking N = 2, this applies to any choice of qi that are not powers of 2.
Remark 2.8. Continuing from remark 2.7, we take N = 2, let qi be the sequence of all odd primes, and apply the weak convergence of measures to the function ![]() $f=\mathbf{1}_{\operatorname{Tr} \equiv 0\ (\mathrm{mod}\ 2)}$, where
$f=\mathbf{1}_{\operatorname{Tr} \equiv 0\ (\mathrm{mod}\ 2)}$, where
 \begin{equation*}\operatorname{Tr}(x^{2g}-a_{2g-1}x^{2g-1}+\cdots+a_0)=a_{2g-1}.\end{equation*}
\begin{equation*}\operatorname{Tr}(x^{2g}-a_{2g-1}x^{2g-1}+\cdots+a_0)=a_{2g-1}.\end{equation*} In this way, if C is a curve over ![]() $\mathbb{F}_q$,
$\mathbb{F}_q$,
 \begin{equation*}
f(\operatorname{charpol}_2(C))=
\begin{cases}
1, \text{if } \operatorname{Tr}(C) := q+1-\#C(\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2) \\
0, \text{otherwise.}
\end{cases}
\end{equation*}
\begin{equation*}
f(\operatorname{charpol}_2(C))=
\begin{cases}
1, \text{if } \operatorname{Tr}(C) := q+1-\#C(\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2) \\
0, \text{otherwise.}
\end{cases}
\end{equation*} Note that this means ![]() $f(\operatorname{charpol}_2(C))=1$ if and only if
$f(\operatorname{charpol}_2(C))=1$ if and only if ![]() $\#C(\mathbb{F}_q)$ is even. Applying theorem 2.1 to the case of the naive measure
$\#C(\mathbb{F}_q)$ is even. Applying theorem 2.1 to the case of the naive measure  $\mathbb{P}^{\operatorname{naive}}_{g, q}$, we obtain the convergence of
$\mathbb{P}^{\operatorname{naive}}_{g, q}$, we obtain the convergence of
 \begin{equation*}
\frac{1}{\#\mathcal{M}_g(\mathbb{F}_q)} \sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}_2(C)) = \frac{\#\{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) \equiv 0\ (\mathrm{mod}\ 2)\}}{\#\mathcal{M}_g(\mathbb{F}_q)}
\end{equation*}
\begin{equation*}
\frac{1}{\#\mathcal{M}_g(\mathbb{F}_q)} \sum_{C \in \mathcal{M}_g(\mathbb{F}_q)} f(\operatorname{charpol}_2(C)) = \frac{\#\{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) \equiv 0\ (\mathrm{mod}\ 2)\}}{\#\mathcal{M}_g(\mathbb{F}_q)}
\end{equation*}to
 \begin{align*}
&\mu^{1}_2\left( \{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \} \right) \\
&\quad = \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z})}.
\end{align*}
\begin{align*}
&\mu^{1}_2\left( \{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \} \right) \\
&\quad = \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z})}.
\end{align*}Thus, we have proven
 \begin{align*}
&\lim_{q \to \infty} \frac{\#\{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) \equiv 0\ (\mathrm{mod}\ 2)\}}{\#\mathcal{M}_g(\mathbb{F}_q)} \\
&\quad = \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z})},
\end{align*}
\begin{align*}
&\lim_{q \to \infty} \frac{\#\{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) \equiv 0\ (\mathrm{mod}\ 2)\}}{\#\mathcal{M}_g(\mathbb{F}_q)} \\
&\quad = \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z}) : \operatorname{Tr}(M) \equiv 0\ (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{Z}/2\mathbb{Z})},
\end{align*}where the limit is taken along the sequence of odd primes (or of their powers).
Remark 2.9. Theorem 2.1 implies theorem 1.4, at least when the order q of the finite field is sufficiently large compared to g. For simplicity, we only discuss the case of odd q. Using [Reference Kirby32], or equivalently [Reference Rivin45, theorem A.1] (see also proposition 6.3 and remark 6.4), one checks that the set of characteristic polynomials of matrices in ![]() $\operatorname{GSp}_{2g}(\mathbb{F}_2)$ is the
$\operatorname{GSp}_{2g}(\mathbb{F}_2)$ is the ![]() $\mathbb{F}_2$-vector space of reciprocal polynomials (which has dimension g + 1). Theorem 2.1 with N = 2 implies that, if
$\mathbb{F}_2$-vector space of reciprocal polynomials (which has dimension g + 1). Theorem 2.1 with N = 2 implies that, if ![]() $q \gg_g 1$, all characteristic polynomials of elements in
$q \gg_g 1$, all characteristic polynomials of elements in ![]() $\operatorname{GSp}_{2g}(\mathbb{F}_2)$ are also the reduction modulo 2 of the characteristic polynomial of Frobenius corresponding to some curve
$\operatorname{GSp}_{2g}(\mathbb{F}_2)$ are also the reduction modulo 2 of the characteristic polynomial of Frobenius corresponding to some curve ![]() $C/\mathbb{F}_q$. This immediately implies that the
$C/\mathbb{F}_q$. This immediately implies that the ![]() $\mathbb{Q}$-vector space
$\mathbb{Q}$-vector space ![]() $L_g(\mathbb{F}_q)$ of theorem 1.4 has dimension at least g + 1.
$L_g(\mathbb{F}_q)$ of theorem 1.4 has dimension at least g + 1.
3. A conjecture on the distribution of  $\#C(\mathbb{F}_q)$
$\#C(\mathbb{F}_q)$
In this section, we describe a heuristic (motivated by the Lang–Trotter philosophy and by results of Gekeler [Reference Gekeler23] in genus 1) that gives precise predictions for the number of (smooth projective) curves over a finite field with a given number of rational points. We define the trace of a curve ![]() $C/\mathbb{F}_q$ by the formula
$C/\mathbb{F}_q$ by the formula
by the Hasse–Weil bound, ![]() $\operatorname{Tr}(C)$ is an integer in the interval
$\operatorname{Tr}(C)$ is an integer in the interval ![]() $[-2g\sqrt{q}, 2g\sqrt{q}]$.
$[-2g\sqrt{q}, 2g\sqrt{q}]$.
We begin by recalling the definition of the Sato–Tate measure on the real interval ![]() $[-2g, 2g]$. Consider the complex Lie group
$[-2g, 2g]$. Consider the complex Lie group ![]() $\operatorname{GSp}_{2g}(\mathbb{C})$ and let
$\operatorname{GSp}_{2g}(\mathbb{C})$ and let ![]() $\operatorname{USp}_{2g}$ be the maximal compact subgroup of
$\operatorname{USp}_{2g}$ be the maximal compact subgroup of ![]() $\operatorname{GSp}_{2g}(\mathbb{C})$ given by unitary symplectic matrices. The group
$\operatorname{GSp}_{2g}(\mathbb{C})$ given by unitary symplectic matrices. The group ![]() $\operatorname{USp}_{2g}$, being compact, is canonically equipped with a unique Haar measure
$\operatorname{USp}_{2g}$, being compact, is canonically equipped with a unique Haar measure ![]() $\mu_{\operatorname{USp}_{2g}}$ normalized so that
$\mu_{\operatorname{USp}_{2g}}$ normalized so that  $\mu_{\operatorname{USp}_{2g}}(\operatorname{USp}_{2g})=1$.
$\mu_{\operatorname{USp}_{2g}}(\operatorname{USp}_{2g})=1$.
The trace map ![]() $\operatorname{tr} : \operatorname{USp}_{2g} \to \mathbb{C}$ has image contained in the real interval
$\operatorname{tr} : \operatorname{USp}_{2g} \to \mathbb{C}$ has image contained in the real interval ![]() $[-2g, 2g]$. We denote by
$[-2g, 2g]$. We denote by  $d\operatorname{ST}_g := \operatorname{tr}_* \mu_{\operatorname{USp}_{2g}}$ the pushforward of the Haar measure of
$d\operatorname{ST}_g := \operatorname{tr}_* \mu_{\operatorname{USp}_{2g}}$ the pushforward of the Haar measure of ![]() $\operatorname{USp}_{2g}$ along the trace map, and we call it the Sato–Tate measure in dimension g. It can be shown (for example using [Reference Serre48, lemma 8.5]) that
$\operatorname{USp}_{2g}$ along the trace map, and we call it the Sato–Tate measure in dimension g. It can be shown (for example using [Reference Serre48, lemma 8.5]) that ![]() $d\operatorname{ST}_g$ is absolutely continuous with respect to the Lebesgue measure, so we also denote by
$d\operatorname{ST}_g$ is absolutely continuous with respect to the Lebesgue measure, so we also denote by ![]() $\operatorname{ST}_g : [-2g, 2g] \to \mathbb{R}$ the density function of
$\operatorname{ST}_g : [-2g, 2g] \to \mathbb{R}$ the density function of ![]() $d\operatorname{ST}_g$.
$d\operatorname{ST}_g$.
Remark 3.1. Explicit expressions for the function ![]() $\operatorname{ST}_2(x)$ can be found in [Reference Lachaud34], see in particular theorem 5.2 of op. cit. We discuss the computation of
$\operatorname{ST}_2(x)$ can be found in [Reference Lachaud34], see in particular theorem 5.2 of op. cit. We discuss the computation of ![]() $\operatorname{ST}_g(x)$ for general g in remark 3.16.
$\operatorname{ST}_g(x)$ for general g in remark 3.16.
Let ![]() $g\geq2$ and let
$g\geq2$ and let ![]() $q=p^n$ be an odd prime power. We now introduce certain local factors, both at infinity and for each finite prime. We motivate the choice of these factors in remarks 3.5 and 3.8. First we need some notation: for an integer t and a prime
$q=p^n$ be an odd prime power. We now introduce certain local factors, both at infinity and for each finite prime. We motivate the choice of these factors in remarks 3.5 and 3.8. First we need some notation: for an integer t and a prime ![]() $\ell \neq p$, we define
$\ell \neq p$, we define
Similarly, for any prime ![]() $\ell$ (including
$\ell$ (including ![]() $\ell=p$), we define
$\ell=p$), we define
 \begin{equation*}
\operatorname{GSp}_{2g, \mathbb{Q}_\ell}^q(\mathbb{Q}_\ell) = \{M \in \operatorname{GSp}_{2g}(\mathbb{Q}_\ell) : \operatorname{mult} M=q \}
\end{equation*}
\begin{equation*}
\operatorname{GSp}_{2g, \mathbb{Q}_\ell}^q(\mathbb{Q}_\ell) = \{M \in \operatorname{GSp}_{2g}(\mathbb{Q}_\ell) : \operatorname{mult} M=q \}
\end{equation*}and
These notations are compatible with our later general definition of  $\operatorname{GSp}_{2g, R}^q$ and
$\operatorname{GSp}_{2g, R}^q$ and ![]() $X_t^q$, see notation 4.1 and definition 4.3. We are now ready to introduce our local factors. Given an integer t, we set
$X_t^q$, see notation 4.1 and definition 4.3. We are now ready to introduce our local factors. Given an integer t, we set
For each prime ![]() $\ell \neq p$, we define
$\ell \neq p$, we define
 \begin{equation}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\# \operatorname{Im}\left( X_t^q(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))},
\end{equation}
\begin{equation}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\# \operatorname{Im}\left( X_t^q(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))},
\end{equation} while for ![]() $\ell=p$ we set
$\ell=p$ we set
 \begin{equation}
\nu_{p}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_p) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( \operatorname{GSp}_{2g, \mathbb{Q}_p}^q(\mathbb{Q}_p) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z}) \right) / p^k}.
\end{equation}
\begin{equation}
\nu_{p}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_p) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( \operatorname{GSp}_{2g, \mathbb{Q}_p}^q(\mathbb{Q}_p) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z}) \right) / p^k}.
\end{equation} In these formulas,  $X_t^q(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ and
$X_t^q(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ and ![]() $\operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z})$ are the natural reduction maps modulo
$\operatorname{Mat}_{2g}(\mathbb{Z}_p) \to \operatorname{Mat}_{2g}(\mathbb{Z}/p^k\mathbb{Z})$ are the natural reduction maps modulo ![]() $\ell^k$ (or pk), and
$\ell^k$ (or pk), and ![]() $\operatorname{Im}$ denotes the image of a function.
$\operatorname{Im}$ denotes the image of a function.
Remark 3.2. The limit in the definition of ![]() $\nu_{\ell}(q,t)$, including for
$\nu_{\ell}(q,t)$, including for ![]() $\ell=p$, exists thanks to [Reference Oesterlé44, théorème 2] (see also [Reference Serre47, equation (62), p. 348, Section 3]). Indeed, the
$\ell=p$, exists thanks to [Reference Oesterlé44, théorème 2] (see also [Reference Serre47, equation (62), p. 348, Section 3]). Indeed, the ![]() $\mathbb{Q}_\ell$-variety defined by
$\mathbb{Q}_\ell$-variety defined by  $\{\tilde{M} \in \operatorname{GSp}_{2g}(\mathbb{Q}_\ell) : \operatorname{Tr}(\tilde M)=t, \operatorname{mult} \tilde{M} = q \}$ has dimension
$\{\tilde{M} \in \operatorname{GSp}_{2g}(\mathbb{Q}_\ell) : \operatorname{Tr}(\tilde M)=t, \operatorname{mult} \tilde{M} = q \}$ has dimension  $d := \dim \operatorname{GSp}_{2g, \mathbb{Q}_\ell}-2$, so by Oesterlé’s theorem [Reference Oesterlé44, théorème 2] the numerators of (7) and (8) are asymptotic to
$d := \dim \operatorname{GSp}_{2g, \mathbb{Q}_\ell}-2$, so by Oesterlé’s theorem [Reference Oesterlé44, théorème 2] the numerators of (7) and (8) are asymptotic to ![]() $c \ell^{dk}$ for some constant c. For a similar reason, the denominators also admit an asymptotic of the form
$c \ell^{dk}$ for some constant c. For a similar reason, the denominators also admit an asymptotic of the form ![]() $c' \ell^{dk}$ for some constant cʹ (this is also easy to prove directly, at least for the case
$c' \ell^{dk}$ for some constant cʹ (this is also easy to prove directly, at least for the case ![]() $\ell \neq p$). Therefore, the ratio converges when
$\ell \neq p$). Therefore, the ratio converges when ![]() $k \to \infty$. We justify the definition given in Eq. (8) in remark 3.8.
$k \to \infty$. We justify the definition given in Eq. (8) in remark 3.8.
We will work under the assumption that ![]() $q \gt 4g^2-1$; see remark 3.9 for a discussion of what happens when q is small with respect to g. Let
$q \gt 4g^2-1$; see remark 3.9 for a discussion of what happens when q is small with respect to g. Let
 \begin{equation}
\nu(q,t)=\nu_\infty(q, t)\prod_{\ell \lt \infty}\nu_{\ell}(q, t).
\end{equation}
\begin{equation}
\nu(q,t)=\nu_\infty(q, t)\prod_{\ell \lt \infty}\nu_{\ell}(q, t).
\end{equation} Notice that ![]() $\nu_\infty(q, t)=0$ for
$\nu_\infty(q, t)=0$ for ![]() $t\notin[-2g\sqrt{q}, 2g\sqrt{q}]$ and in particular
$t\notin[-2g\sqrt{q}, 2g\sqrt{q}]$ and in particular ![]() $\nu(q,t)$ is non-zero for finitely many t (for a fixed q). The fact that the product (9) converges for all t is far from obvious. We will show this in §4. Define
$\nu(q,t)$ is non-zero for finitely many t (for a fixed q). The fact that the product (9) converges for all t is far from obvious. We will show this in §4. Define
 \begin{equation}
\nu'(q,t)=\frac{\nu(q,t)}{\sum_{t\in \mathbb{Z}}\nu(q,t)}.
\end{equation}
\begin{equation}
\nu'(q,t)=\frac{\nu(q,t)}{\sum_{t\in \mathbb{Z}}\nu(q,t)}.
\end{equation}The denominator is non-zero, as we will show in lemma 4.9. By definition, we have
 \begin{equation*}
\sum_{t\in \mathbb{Z}}\nu'(q,t)=1.
\end{equation*}
\begin{equation*}
\sum_{t\in \mathbb{Z}}\nu'(q,t)=1.
\end{equation*}Definition 3.3. Let ![]() $g\geq2$, let q be an odd prime power, and let t be an integer. Denote by
$g\geq2$, let q be an odd prime power, and let t be an integer. Denote by ![]() $H(q,t)$ the number of isomorphism classes of (smooth projective) curves of genus g defined over
$H(q,t)$ the number of isomorphism classes of (smooth projective) curves of genus g defined over ![]() $\mathbb{F}_q$ with trace t, that is, for which
$\mathbb{F}_q$ with trace t, that is, for which ![]() $q+1-\#C(\mathbb{F}_q)=t$. Define
$q+1-\#C(\mathbb{F}_q)=t$. Define
 \begin{equation}
H'(q,t)=\frac{H(q,t)}{\sum_{t\in \mathbb{Z}}H(q,t)} = \frac{H(q,t)}{\#\mathcal{M}_g(\mathbb{F}_q)} = \mathbb{P}^{\operatorname{naive}}_{g, q} \left( \{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) = t\} \right).
\end{equation}
\begin{equation}
H'(q,t)=\frac{H(q,t)}{\sum_{t\in \mathbb{Z}}H(q,t)} = \frac{H(q,t)}{\#\mathcal{M}_g(\mathbb{F}_q)} = \mathbb{P}^{\operatorname{naive}}_{g, q} \left( \{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) = t\} \right).
\end{equation} Thus, ![]() $H'(q,t)$ is the ‘naive probability’ that a curve of genus g, defined over
$H'(q,t)$ is the ‘naive probability’ that a curve of genus g, defined over ![]() $\mathbb{F}_q$, has trace t.
$\mathbb{F}_q$, has trace t.
Notice that ![]() $H'(q, t)=0$ for
$H'(q, t)=0$ for ![]() $t\notin[-2g\sqrt{q}, 2g\sqrt{q}]$. We conjecture that, for fixed g, as
$t\notin[-2g\sqrt{q}, 2g\sqrt{q}]$. We conjecture that, for fixed g, as ![]() $q \to \infty$ the measures
$q \to \infty$ the measures ![]() $\nu^{\prime}(q,t)$ and
$\nu^{\prime}(q,t)$ and ![]() $H'(q,t)$ converge to one another. To make this precise, we use the L 1-norm on the space of probability measures on
$H'(q,t)$ converge to one another. To make this precise, we use the L 1-norm on the space of probability measures on ![]() $\mathbb{Z}$: since
$\mathbb{Z}$: since ![]() $\mathbb{Z}$ is countable, we define the L 1 distance
$\mathbb{Z}$ is countable, we define the L 1 distance ![]() $d(\mu_1, \mu_2)$ between two probability measures as
$d(\mu_1, \mu_2)$ between two probability measures as
 \begin{equation*}
d(\mu_1, \mu_2) := \sum_{t \in \mathbb{Z}}\left|\mu_1(t) - \mu_2(t)\right|.
\end{equation*}
\begin{equation*}
d(\mu_1, \mu_2) := \sum_{t \in \mathbb{Z}}\left|\mu_1(t) - \mu_2(t)\right|.
\end{equation*}By [Reference Levin and Peres41, proposition 4.2], the L 1 distance is equal up to a factor of 2 to another natural distance on the space of probability measures, namely the total variation distance
 \begin{equation*}
d^{\operatorname{tot.var.}}(\mu_1, \mu_2) = \sup_{A \subseteq \mathbb{Z}} \left|\mu_1(A) - \mu_2(A)\right|.
\end{equation*}
\begin{equation*}
d^{\operatorname{tot.var.}}(\mu_1, \mu_2) = \sup_{A \subseteq \mathbb{Z}} \left|\mu_1(A) - \mu_2(A)\right|.
\end{equation*} We can now formulate our conjecture: we phrase it in terms of d, but clearly we obtain an equivalent statement by replacing d with ![]() $d^{\operatorname{tot.var.}}$
$d^{\operatorname{tot.var.}}$
Conjecture 3.4
Fix an integer ![]() $g\geq2$. As
$g\geq2$. As ![]() $q \to \infty$ along prime powers, we have
$q \to \infty$ along prime powers, we have
where ![]() $H'(q,\cdot)$ and
$H'(q,\cdot)$ and ![]() $\nu^{\prime}(q, \cdot)$ are considered as probability measures on
$\nu^{\prime}(q, \cdot)$ are considered as probability measures on ![]() $\mathbb{Z}$.
$\mathbb{Z}$.
Remark 3.5. We now give our reasons for believing in conjecture 3.4. First of all, notice that by corollary 2.6 one may as well state conjecture 3.4 using the intrinsic measure  $\mathbb{P}^{\operatorname{intr}}_{g, q}$.
$\mathbb{P}^{\operatorname{intr}}_{g, q}$.
1. For the case of elliptic curves and the intrinsic measure
 $\mathbb{P}^{\operatorname{intr}}_{g, q}$, the analogue of our conjecture has been proved in [Reference Gekeler23, theorem 5.5], at least when q is a prime number. In the proof, the author computes the value of
$\mathbb{P}^{\operatorname{intr}}_{g, q}$, the analogue of our conjecture has been proved in [Reference Gekeler23, theorem 5.5], at least when q is a prime number. In the proof, the author computes the value of  $\nu^{\prime}(q,t)$ (see [Reference Gekeler23, corollary 4.8]) and shows that it is equal to
$\nu^{\prime}(q,t)$ (see [Reference Gekeler23, corollary 4.8]) and shows that it is equal to  $H'(q,t)$, which is computed in [Reference Deuring20].
$H'(q,t)$, which is computed in [Reference Deuring20].2. Let C be a curve of genus g defined over
 $\mathbb{F}_q$. The trace t of C modulo
$\mathbb{F}_q$. The trace t of C modulo  $\ell^k$ is equal to the trace of the matrix
$\ell^k$ is equal to the trace of the matrix  $M\in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ that represents the action of the Frobenius
$M\in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ that represents the action of the Frobenius  $\operatorname{Frob}_q$ on the
$\operatorname{Frob}_q$ on the  $\ell^k$-torsion points of the Jacobian of C. Notice that there exists
$\ell^k$-torsion points of the Jacobian of C. Notice that there exists  $\tilde{M} \in \operatorname{GSp}_{2g}(\mathbb{Z}_\ell)$ such that
$\tilde{M} \in \operatorname{GSp}_{2g}(\mathbb{Z}_\ell)$ such that  $\tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^k})$ with
$\tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^k})$ with  $\operatorname{tr}(\tilde{M})=t$ and
$\operatorname{tr}(\tilde{M})=t$ and  $\operatorname{mult}(\tilde{M})=q$: indeed, it suffices to take as
$\operatorname{mult}(\tilde{M})=q$: indeed, it suffices to take as  $\tilde{M}$ the matrix representing the action of Frobenius on the full Tate module
$\tilde{M}$ the matrix representing the action of Frobenius on the full Tate module  $T_\ell \operatorname{Jac}(C) \cong \mathbb{Z}_\ell^{2g}$. Hence, by theorem 2.1, as
$T_\ell \operatorname{Jac}(C) \cong \mathbb{Z}_\ell^{2g}$. Hence, by theorem 2.1, as  $q \to \infty$ the probability that a curve C has trace t modulo
$q \to \infty$ the probability that a curve C has trace t modulo  $\ell^k$ converges to
$\ell^k$ converges to
 \begin{equation*}
\frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) :
\operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}.
\end{equation*}
\begin{equation*}
\frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) :
\operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}.
\end{equation*}Taking the limit
 $k \to \infty$,
$k \to \infty$,  $\nu_\ell(q,t)$ should represent the probability that, given a random curve C, the Frobenius endomorphism acts on the
$\nu_\ell(q,t)$ should represent the probability that, given a random curve C, the Frobenius endomorphism acts on the  $\ell^\infty$-torsion points of the Jacobian of the curve with trace t. (The numerator of
$\ell^\infty$-torsion points of the Jacobian of the curve with trace t. (The numerator of  $\nu_\ell(q,t)$ counts those matrices in
$\nu_\ell(q,t)$ counts those matrices in  $\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ with trace t and multiplier q which can be lifted to
$\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ with trace t and multiplier q which can be lifted to  $X^q_t(\mathbb{Z}_\ell)$. See remark 3.14 for this condition and remark 3.8 for the case
$X^q_t(\mathbb{Z}_\ell)$. See remark 3.14 for this condition and remark 3.8 for the case  $\ell=p$).
$\ell=p$).Our conjecture can then be seen as a minimalist one: we are essentially claiming that the distributions of the trace of Frobenius in
 $\mathbb{Z}_\ell$ for different primes
$\mathbb{Z}_\ell$ for different primes  $\ell$ are independent of each other (which we know is the case by theorem 2.1, at least for
$\ell$ are independent of each other (which we know is the case by theorem 2.1, at least for  $\ell \neq p$), and that (as
$\ell \neq p$), and that (as  $q \to \infty$) they also become independent of the distribution of the absolute value of
$q \to \infty$) they also become independent of the distribution of the absolute value of  $\operatorname{Tr}(\operatorname{Frob}) \in \mathbb{R}$. To put it in another way, conjecture 3.4 is the simplest joint distribution that reproduces the correct (known) ‘marginal’ distributions for
$\operatorname{Tr}(\operatorname{Frob}) \in \mathbb{R}$. To put it in another way, conjecture 3.4 is the simplest joint distribution that reproduces the correct (known) ‘marginal’ distributions for  $\operatorname{Tr}(C) \bmod N$ and for
$\operatorname{Tr}(C) \bmod N$ and for  $\frac{|\operatorname{Tr}(C)|}{|\sqrt{q}|} \in [-2g,2g]$.
$\frac{|\operatorname{Tr}(C)|}{|\sqrt{q}|} \in [-2g,2g]$.3. The ‘minimalist’ philosophy just outlined is, of course, the same that underlies the widely believed Lang–Trotter conjecture [Reference Lang and Trotter36, Part I, Section 3].
4. Finally, numerical evidence points in the direction of the conjecture being true, see §3.2.
Our conjecture should be contrasted with [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1], which makes a different prediction for ![]() $H'(q,t)$. The authors of [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9] define (the analogue of our)
$H'(q,t)$. The authors of [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9] define (the analogue of our) ![]() $\nu(q,t)$ purely in terms of the Sato–Tate density
$\nu(q,t)$ purely in terms of the Sato–Tate density ![]() $\nu_\infty$. We believe that—as happens for g = 1—one should also take into account the measures
$\nu_\infty$. We believe that—as happens for g = 1—one should also take into account the measures ![]() $\nu_\ell$ for all finite
$\nu_\ell$ for all finite ![]() $\ell$. In fact, even though we cannot prove conjecture 3.4, the results of §2 are enough to show that [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] is not correct. The proof of this fact is a bit technical: [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] refers only to non-hyperelliptic curves and replaces
$\ell$. In fact, even though we cannot prove conjecture 3.4, the results of §2 are enough to show that [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] is not correct. The proof of this fact is a bit technical: [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] refers only to non-hyperelliptic curves and replaces ![]() $t/\sqrt{q}$ with the nearest integer, both of which introduce formal difficulties. However, the key idea is comparatively simple, so we isolate it in the next proposition, which shows that the measures
$t/\sqrt{q}$ with the nearest integer, both of which introduce formal difficulties. However, the key idea is comparatively simple, so we isolate it in the next proposition, which shows that the measures ![]() $\nu_\infty$ and Hʹ are substantially different infinitely often. Intuitively, this contradicts [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1]. A complete argument showing that [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] does not hold is given in the preprint version of this article [Reference Ballini, Lombardo and Verzobio8]. In particular, in [Reference Ballini, Lombardo and Verzobio8, Appendix A], we prove all the technical details necessary to show that an argument very similar to that of proposition 3.6 disproves [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1]. For the sake of brevity, and since that proof does not add much to the mathematical content of the article, we decided to omit it here. The following proposition is stated for g = 3, but we suspect it should hold for all
$\nu_\infty$ and Hʹ are substantially different infinitely often. Intuitively, this contradicts [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1]. A complete argument showing that [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1] does not hold is given in the preprint version of this article [Reference Ballini, Lombardo and Verzobio8]. In particular, in [Reference Ballini, Lombardo and Verzobio8, Appendix A], we prove all the technical details necessary to show that an argument very similar to that of proposition 3.6 disproves [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1]. For the sake of brevity, and since that proof does not add much to the mathematical content of the article, we decided to omit it here. The following proposition is stated for g = 3, but we suspect it should hold for all ![]() $g\geq 3$.
$g\geq 3$.
Proposition 3.6. Let g = 3. There exists ɛ > 0 such that for all odd prime powers q bigger than a constant ![]() $q_0 \gt 0$ there exists
$q_0 \gt 0$ there exists ![]() $t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z}$ such that
$t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z}$ such that
 \begin{equation*}
\left| \sqrt{q}\mathbb{P}^{\operatorname{naive}}_{g, q}( \operatorname{Tr} C/\mathbb{F}_q = t) - \operatorname{ST}_g(t/\sqrt{q}) \right| \geq \varepsilon.
\end{equation*}
\begin{equation*}
\left| \sqrt{q}\mathbb{P}^{\operatorname{naive}}_{g, q}( \operatorname{Tr} C/\mathbb{F}_q = t) - \operatorname{ST}_g(t/\sqrt{q}) \right| \geq \varepsilon.
\end{equation*}Proof. We denote simply by ![]() $\mathbb{P}$ the naive probability measure
$\mathbb{P}$ the naive probability measure  $\mathbb{P}^{\operatorname{naive}}_{g, q}$ on
$\mathbb{P}^{\operatorname{naive}}_{g, q}$ on ![]() $\mathcal{M}_{g}(\mathbb{F}_q)$. We assume that
$\mathcal{M}_{g}(\mathbb{F}_q)$. We assume that
one has
 \begin{equation}
\left| \mathbb{P}( \operatorname{Tr} C/\mathbb{F}_q = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right| \lt \frac{\varepsilon}{\sqrt{q}}
\end{equation}
\begin{equation}
\left| \mathbb{P}( \operatorname{Tr} C/\mathbb{F}_q = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right| \lt \frac{\varepsilon}{\sqrt{q}}
\end{equation} and aim for a contradiction. Fix ɛ > 0 and let p be an odd prime. Let ![]() $q=p^n$. We have
$q=p^n$. We have
 \begin{equation*}
\begin{aligned}
&\mathbb{P}( \operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) \\
&\quad = \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \left( \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} + \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right) \\
& \quad = \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \\
&\qquad + \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2)}} \left( \mathbb{P}(\operatorname{Tr} C/\mathbb{F}_q = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right) \\
& \quad = \frac{1}{\sqrt{q}} \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \operatorname{ST}_g(t/\sqrt{q}) + E,
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
&\mathbb{P}( \operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) \\
&\quad = \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \left( \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} + \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right) \\
& \quad = \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \\
&\qquad + \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2)}} \left( \mathbb{P}(\operatorname{Tr} C/\mathbb{F}_q = t) - \frac{\operatorname{ST}_g(t/\sqrt{q})}{\sqrt{q}} \right) \\
& \quad = \frac{1}{\sqrt{q}} \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \operatorname{ST}_g(t/\sqrt{q}) + E,
\end{aligned}
\end{equation*}with
 \begin{equation}|E| \leq (4g+1)\sqrt{q} \cdot \frac{\varepsilon}{\sqrt{q}} \leq (4g+1)\varepsilon\end{equation}
\begin{equation}|E| \leq (4g+1)\sqrt{q} \cdot \frac{\varepsilon}{\sqrt{q}} \leq (4g+1)\varepsilon\end{equation} by (13). On the other hand, some basic analysis shows that (since ![]() $\operatorname{ST}_g$ is Riemann-integrable)
$\operatorname{ST}_g$ is Riemann-integrable)
 \begin{equation*}\frac{1}{\sqrt{q}} \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \operatorname{ST}_g(t/\sqrt{q})\end{equation*}
\begin{equation*}\frac{1}{\sqrt{q}} \sum_{\substack{t \in [-2g\sqrt{q}, 2g\sqrt{q}] \cap \mathbb{Z} \\ t \equiv 0\ (\mathrm{mod}\ 2) }} \operatorname{ST}_g(t/\sqrt{q})\end{equation*} converges, as ![]() $q=p^n$ goes to infinity, to
$q=p^n$ goes to infinity, to
 \begin{equation*}
\frac{1}{2\sqrt{q}} \int_{-2g\sqrt{q}}^{2g\sqrt{q}} \operatorname{ST}_g(t/\sqrt{q}) dt =\frac{1}{2} \int_{-2g}^{2g} \operatorname{ST}_g(t) dt = \frac{1}{2}.
\end{equation*}
\begin{equation*}
\frac{1}{2\sqrt{q}} \int_{-2g\sqrt{q}}^{2g\sqrt{q}} \operatorname{ST}_g(t/\sqrt{q}) dt =\frac{1}{2} \int_{-2g}^{2g} \operatorname{ST}_g(t) dt = \frac{1}{2}.
\end{equation*}Therefore,
 \begin{equation}
\left|\mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2))-\frac 12\right|\leq \left|E\right|+\varepsilon
\end{equation}
\begin{equation}
\left|\mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2))-\frac 12\right|\leq \left|E\right|+\varepsilon
\end{equation} for ![]() $q=p^n$ large enough.
Let
$q=p^n$ large enough.
Let
 \begin{equation*}\begin{aligned}
L_1(g)&:= \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{F}_2) : \operatorname{Tr} M \equiv 0 \quad \ (\mathrm{mod}\ 2), \operatorname{mult} M = q \equiv 1 \quad (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{F}_2)}.
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
L_1(g)&:= \frac{\#\{M \in \operatorname{GSp}_{2g}(\mathbb{F}_2) : \operatorname{Tr} M \equiv 0 \quad \ (\mathrm{mod}\ 2), \operatorname{mult} M = q \equiv 1 \quad (\mathrm{mod}\ 2) \}}{\#\operatorname{GSp}_{2g}(\mathbb{F}_2)}.
\end{aligned}
\end{equation*} Note that the condition ![]() $\operatorname{mult} M = q \equiv 1\ (\mathrm{mod}\ 2)$ is actually automatic, since 1 is the only invertible element in
$\operatorname{mult} M = q \equiv 1\ (\mathrm{mod}\ 2)$ is actually automatic, since 1 is the only invertible element in ![]() $\mathbb{F}_2$. By remark 2.8, as
$\mathbb{F}_2$. By remark 2.8, as ![]() $q \to \infty$ we have
$q \to \infty$ we have ![]() $
\left|L_1(g) - \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) \right| = o(1),
$ and in particular, for q large enough, we have
$
\left|L_1(g) - \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) \right| = o(1),
$ and in particular, for q large enough, we have
We now prove that the initial claim does not hold for g = 3. It seems likely that a similar strategy can be applied for every g > 3. By direct computation,  $L_1(3) = \frac{1436}{2835} \approx 0.5065\ldots$ is strictly greater than
$L_1(3) = \frac{1436}{2835} \approx 0.5065\ldots$ is strictly greater than ![]() $1/2$. Fix
$1/2$. Fix  $0 \lt \varepsilon \lt \frac{|L_1(g)-1/2|}{8g}$ for g = 3. For
$0 \lt \varepsilon \lt \frac{|L_1(g)-1/2|}{8g}$ for g = 3. For ![]() $q=p^n$ large enough, by Eqs. (14), (15), and (16), we get
$q=p^n$ large enough, by Eqs. (14), (15), and (16), we get
 \begin{equation*}
\begin{aligned}
\left|L_1(3) - \frac{1}{2}\right| & \leq \left|L_1(3) - \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2))\right| \\
&\quad + \left|\mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) - \frac{1}{2}\right| \\
& \leq \left|E\right|+2\varepsilon \leq (4g+3)\varepsilon \lt \left|L_1(3)-\frac 12\right|,
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\left|L_1(3) - \frac{1}{2}\right| & \leq \left|L_1(3) - \mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2))\right| \\
&\quad + \left|\mathbb{P}(\operatorname{Tr} (C/\mathbb{F}_q) \equiv 0\ (\mathrm{mod}\ 2)) - \frac{1}{2}\right| \\
& \leq \left|E\right|+2\varepsilon \leq (4g+3)\varepsilon \lt \left|L_1(3)-\frac 12\right|,
\end{aligned}
\end{equation*}contradiction.
3.1. Further remarks on conjecture 3.4
In this section, we collect several other remarks on conjecture 3.4 and the possible limits of its validity. As all the material in this section is speculative, we do not go into much detail, but we hope that this discussion will encourage others to investigate the issues raised here.
Since the statistics of the distribution of the trace of principally polarized abelian varieties (PPAVs) of a fixed dimension g over finite fields are the same as those of Jacobians (equivalently, of curves of genus g), it seems reasonable to extend conjecture 3.4 to the family of all PPAVs of a fixed dimension. More precisely and more generally, we formulate the following conjecture, of which conjecture 3.4 is a special case.
Conjecture 3.7
Let U be a scheme of finite type over ![]() $\mathbb{Z}$ and let
$\mathbb{Z}$ and let ![]() $\mathcal{A} \to U$ be a family of g-dimensional, PPAVs with full monodromy. For a prime power q, let
$\mathcal{A} \to U$ be a family of g-dimensional, PPAVs with full monodromy. For a prime power q, let
 \begin{equation*}
H'(q,t) = \frac{\#\{u \in U(\mathbb{F}_q) : q+1-t=\#\mathcal{A}_u(\mathbb{F}_q) \}}{\#U(\mathbb{F}_q)},
\end{equation*}
\begin{equation*}
H'(q,t) = \frac{\#\{u \in U(\mathbb{F}_q) : q+1-t=\#\mathcal{A}_u(\mathbb{F}_q) \}}{\#U(\mathbb{F}_q)},
\end{equation*} seen as a measure on ![]() $\mathbb{Z}$. Let
$\mathbb{Z}$. Let ![]() $\nu^{\prime}$ be as in (10). As
$\nu^{\prime}$ be as in (10). As ![]() $q \to \infty$ along prime powers, we have
$q \to \infty$ along prime powers, we have ![]() $d(H'(q, \cdot), \nu'(q, \cdot)) \to 0$, where
$d(H'(q, \cdot), \nu'(q, \cdot)) \to 0$, where ![]() $H'(q, \cdot)$ and
$H'(q, \cdot)$ and ![]() $\nu^{\prime}(q, \cdot)$ are considered as probability measures on
$\nu^{\prime}(q, \cdot)$ are considered as probability measures on ![]() $\mathbb{Z}$.
$\mathbb{Z}$.
In particular, Gekeler’s results [Reference Gekeler23] should perhaps be interpreted in this light. From this perspective, one should perhaps ask if conjecture 3.4 could not be upgraded to an actual equality for fixed q (as opposed to an asymptotic statement for ![]() $q \to \infty$) when one considers the better-behaved family of all PPAVs. We will see that, while the measures
$q \to \infty$) when one considers the better-behaved family of all PPAVs. We will see that, while the measures ![]() $H'(q,t)$ and
$H'(q,t)$ and ![]() $\nu^{\prime}(q,t)$ cannot be equal in general, even for abelian varieties (remark 3.9), this point of view can still be helpful.
$\nu^{\prime}(q,t)$ cannot be equal in general, even for abelian varieties (remark 3.9), this point of view can still be helpful.
In this section, we mostly focus on conjecture 3.4, but—with minimal modifications—similar comments also apply to conjecture 3.7. Given the limited evidence we have in support of conjecture 3.4, it seems safer to restrict our discussion to the special case of the family of all curves (but we have no reason to expect a substantially different behaviour for any other family of abelian varieties with full monodromy).
Remark 3.8. Local factor at p
We justify the choice of the local factor (8). Observe first that the more general formula
 \begin{equation*}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( \operatorname{GSp}_{2g, \mathbb{Q}_\ell}^q(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) / \ell^k}
\end{equation*}
\begin{equation*}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( \operatorname{GSp}_{2g, \mathbb{Q}_\ell}^q(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) / \ell^k}
\end{equation*} reduces to (7) and (8) respectively when ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $\ell=p$. The denominator of this formula is essentially the average over
$\ell=p$. The denominator of this formula is essentially the average over ![]() $t \in \{0, \ldots, \ell^{k}-1\}$ of the numerator, so the ratio measures the deviation from the average of the number of symplectic matrices with a given trace. For g = 1, Gekeler shows [Reference Gekeler23] that this formula does give the correct local factor at p. For g > 1, at least when the field of definition is the prime field
$t \in \{0, \ldots, \ell^{k}-1\}$ of the numerator, so the ratio measures the deviation from the average of the number of symplectic matrices with a given trace. For g = 1, Gekeler shows [Reference Gekeler23] that this formula does give the correct local factor at p. For g > 1, at least when the field of definition is the prime field ![]() $\mathbb{F}_p$, one can consider the action of Frobenius on rigid (or crystalline) cohomology, which is a free
$\mathbb{F}_p$, one can consider the action of Frobenius on rigid (or crystalline) cohomology, which is a free ![]() $W(\mathbb{F}_p)=\mathbb{Z}_p$-module of rank 2g: in this way, Frobenius acts symplectically on a 2g-dimensional
$W(\mathbb{F}_p)=\mathbb{Z}_p$-module of rank 2g: in this way, Frobenius acts symplectically on a 2g-dimensional ![]() $\mathbb{Q}_p$-vector space (the cohomology group tensored with
$\mathbb{Q}_p$-vector space (the cohomology group tensored with ![]() $\mathbb{Q}_p$) preserving a
$\mathbb{Q}_p$) preserving a ![]() $\mathbb{Z}_p$-lattice, so it defines a matrix with entries in
$\mathbb{Z}_p$-lattice, so it defines a matrix with entries in ![]() $\mathbb{Z}_p$ and multiplier q (any such matrix does not lie in
$\mathbb{Z}_p$ and multiplier q (any such matrix does not lie in ![]() $\operatorname{GSp}_{2g}(\mathbb{Z}_p)$, because the multiplier is not invertible in
$\operatorname{GSp}_{2g}(\mathbb{Z}_p)$, because the multiplier is not invertible in ![]() $\mathbb{Z}_p$—in fact, such a matrix does not even lie in
$\mathbb{Z}_p$—in fact, such a matrix does not even lie in ![]() $\operatorname{GL}_{2g}(\mathbb{Z}_p)$). Note that we cannot simply consider the Frobenius action on the Tate module Tp, because this has rank at most g, so it doesn’t provide a good p-adic analogue of
$\operatorname{GL}_{2g}(\mathbb{Z}_p)$). Note that we cannot simply consider the Frobenius action on the Tate module Tp, because this has rank at most g, so it doesn’t provide a good p-adic analogue of ![]() $T_\ell$ for
$T_\ell$ for ![]() $\ell \neq p$. It seems likely that an equidistribution result similar to theorem 2.3 should also hold in rigid cohomology (see [Reference Hartl and Pal26, Reference Kedlaya30]), which would lead to the local factor (8), just like theorem 2.3 leads to (7), see remark 3.5.
$\ell \neq p$. It seems likely that an equidistribution result similar to theorem 2.3 should also hold in rigid cohomology (see [Reference Hartl and Pal26, Reference Kedlaya30]), which would lead to the local factor (8), just like theorem 2.3 leads to (7), see remark 3.5.
Remark 3.9. (q small with respect to g)
Notice that ![]() $\nu^{\prime}(q, t)$ can be positive also for values of t such that
$\nu^{\prime}(q, t)$ can be positive also for values of t such that ![]() $q+1-t \lt 0$. Of course, this does not make sense, because
$q+1-t \lt 0$. Of course, this does not make sense, because ![]() $q+1-t$ should represent the number of
$q+1-t$ should represent the number of ![]() $\mathbb{F}_q$-rational points of a curve. The point is that the support of
$\mathbb{F}_q$-rational points of a curve. The point is that the support of ![]() $\nu^{\prime}(q,t)$ is the full interval
$\nu^{\prime}(q,t)$ is the full interval ![]() $[-2g\sqrt{q},2g\sqrt{q}]$, and when q is small with respect to g it may well happen that
$[-2g\sqrt{q},2g\sqrt{q}]$, and when q is small with respect to g it may well happen that ![]() $q+1-2g\sqrt{q} \lt 0$.
$q+1-2g\sqrt{q} \lt 0$.
There are also subtler issues. The Sato–Tate distribution arises as the pushforward via the trace map of the Haar measure on ![]() $\operatorname{USp}_{2g}$. Suppose that
$\operatorname{USp}_{2g}$. Suppose that ![]() $M \in \operatorname{USp}_{2g}$ corresponds to the unitarized Frobenius
$M \in \operatorname{USp}_{2g}$ corresponds to the unitarized Frobenius  $\frac{\operatorname{Frob}_{C/\mathbb{F}_q}}{\sqrt{q}}$, where
$\frac{\operatorname{Frob}_{C/\mathbb{F}_q}}{\sqrt{q}}$, where ![]() $C/\mathbb{F}_q$ is a smooth projective curve of genus g. Then, for every
$C/\mathbb{F}_q$ is a smooth projective curve of genus g. Then, for every ![]() $m \geq 1$ one has
$m \geq 1$ one has
 \begin{equation*}
\#C(\mathbb{F}_{q^m}) = q^m+1 - q^{m/2}\operatorname{tr}(M^m),
\end{equation*}
\begin{equation*}
\#C(\mathbb{F}_{q^m}) = q^m+1 - q^{m/2}\operatorname{tr}(M^m),
\end{equation*} and in particular, for all integers ![]() $m_1 \mid m_2$, we must have
$m_1 \mid m_2$, we must have
 \begin{align*}
\#C(\mathbb{F}_{q^{m_1}}) = q^{m_1}+1 - q^{m_1/2}\operatorname{tr}(M^{m_1}) \leq q^{m_2}+1 - q^{m_2/2}\operatorname{tr}(M^{m_2}) = \#C(\mathbb{F}_{q^{m_2}}).
\end{align*}
\begin{align*}
\#C(\mathbb{F}_{q^{m_1}}) = q^{m_1}+1 - q^{m_1/2}\operatorname{tr}(M^{m_1}) \leq q^{m_2}+1 - q^{m_2/2}\operatorname{tr}(M^{m_2}) = \#C(\mathbb{F}_{q^{m_2}}).
\end{align*} When q is small with respect to g, there are matrices in ![]() $\operatorname{USp}_{2g}$ and integers
$\operatorname{USp}_{2g}$ and integers ![]() $m_1 \mid m_2$ for which this inequality does not hold. In this regime, one should perhaps replace the usual Sato–Tate measure with the following. Let X be the subset of
$m_1 \mid m_2$ for which this inequality does not hold. In this regime, one should perhaps replace the usual Sato–Tate measure with the following. Let X be the subset of ![]() $\operatorname{USp}_{2g}$ consisting of those matrices that satisfy all the inequalities
$\operatorname{USp}_{2g}$ consisting of those matrices that satisfy all the inequalities
 \begin{equation*}
0 \leq q^{m_1}+1 - q^{m_1/2}\operatorname{tr}(M^{m_1}) \leq q^{m_2}+1 - q^{m_2/2}\operatorname{tr}(M^{m_2}) = \#C(\mathbb{F}_{q^{m_2}})
\end{equation*}
\begin{equation*}
0 \leq q^{m_1}+1 - q^{m_1/2}\operatorname{tr}(M^{m_1}) \leq q^{m_2}+1 - q^{m_2/2}\operatorname{tr}(M^{m_2}) = \#C(\mathbb{F}_{q^{m_2}})
\end{equation*} for all ![]() $m_1 \mid m_2$. A candidate to replace
$m_1 \mid m_2$. A candidate to replace ![]() $\operatorname{ST}_g$ is the pushforward via the trace of the restriction of the Haar measure to the set X (renormalized so as to have mass 1).
$\operatorname{ST}_g$ is the pushforward via the trace of the restriction of the Haar measure to the set X (renormalized so as to have mass 1).
Recall that we are fixing g and sending q to infinity, so this issue does not affect our conjecture 3.4.
Remark 3.10. Asymmetry of the distribution  $H'(q,t)$
$H'(q,t)$
An advantage of working with PPAVs rather than curves is that the former always admit quadratic twists, which implies that the distribution of their traces is always symmetric around 0. This is further indication that perhaps conjecture 3.4 is more natural for the family of PPAVs. In fact, we remark that while ![]() $\nu^{\prime}(q, t)$ is symmetric (that is,
$\nu^{\prime}(q, t)$ is symmetric (that is, ![]() $\nu^{\prime}(q,-t)=\nu'(q,t)$), this is not necessarily the case for
$\nu^{\prime}(q,-t)=\nu'(q,t)$), this is not necessarily the case for ![]() $H'(q,t)$ as soon as
$H'(q,t)$ as soon as ![]() $g \geq 3$, as one can see for example in [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, figure 4], or below in our own figure 3. See also [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, § 5] for a more extensive discussion of the asymmetry of
$g \geq 3$, as one can see for example in [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, figure 4], or below in our own figure 3. See also [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, § 5] for a more extensive discussion of the asymmetry of ![]() $H'(q,t)$. In particular, we note again that one cannot have an exact equality
$H'(q,t)$. In particular, we note again that one cannot have an exact equality ![]() $H'(q,t)=\nu'(q,t)$ for general g, because the right-hand side is easily seen to be symmetric. All the same, we expect the two measures to be arbitrarily close in the limit
$H'(q,t)=\nu'(q,t)$ for general g, because the right-hand side is easily seen to be symmetric. All the same, we expect the two measures to be arbitrarily close in the limit ![]() $q \to \infty$.
$q \to \infty$.
Remark 3.11. (Speed of convergence)
The limit in conjecture 3.4 cannot converge too quickly. We briefly show why. Given a measure µ on ![]() $\mathbb{Z}$, let
$\mathbb{Z}$, let ![]() $(-1)^*\mu(\cdot)$ be the measure defined as
$(-1)^*\mu(\cdot)$ be the measure defined as ![]() $(-1)^*\mu(t)=\mu(-t)$ for all
$(-1)^*\mu(t)=\mu(-t)$ for all ![]() $t\in \mathbb{Z}$. By definition,
$t\in \mathbb{Z}$. By definition, ![]() $(-1)^*\nu'(q, \cdot)-\nu'(q, \cdot)=0$ since
$(-1)^*\nu'(q, \cdot)-\nu'(q, \cdot)=0$ since ![]() $\nu^{\prime}(q,\cdot)$ is symmetric. In particular, the moments of
$\nu^{\prime}(q,\cdot)$ is symmetric. In particular, the moments of ![]() $(-1)^*(\sqrt{q}\nu'(q, \cdot))-(\sqrt{q}\nu'(q, \cdot))$ are 0 for all q. Assume that
$(-1)^*(\sqrt{q}\nu'(q, \cdot))-(\sqrt{q}\nu'(q, \cdot))$ are 0 for all q. Assume that ![]() $d(H'(q, \cdot), \nu'(q, \cdot))$ converges to zero sufficiently quickly (for example, assume that the difference is
$d(H'(q, \cdot), \nu'(q, \cdot))$ converges to zero sufficiently quickly (for example, assume that the difference is ![]() $O(q^{-k-1})$ for some
$O(q^{-k-1})$ for some ![]() $k \geq 0$): the first 2k moments of
$k \geq 0$): the first 2k moments of ![]() $(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ then also converge to zero as q goes to infinity. By [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, corollary 5.3], the n-th moment of
$(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ then also converge to zero as q goes to infinity. By [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, corollary 5.3], the n-th moment of ![]() $(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ converges, for n odd, to a real number bn and bn is non-zero for n large enough (see [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, proposition 2.3]). Hence, for n large enough, the n-th moment of
$(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ converges, for n odd, to a real number bn and bn is non-zero for n large enough (see [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, proposition 2.3]). Hence, for n large enough, the n-th moment of ![]() $(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ does not tend to zero as q goes to infinity. If
$(-1)^*(\sqrt{q}H'(q, \cdot))-(\sqrt{q}H'(q, \cdot))$ does not tend to zero as q goes to infinity. If ![]() $b_n \neq 0$ and
$b_n \neq 0$ and ![]() $2k \geq n$, this is a contradiction.
$2k \geq n$, this is a contradiction.
We thank Christophe Ritzenthaler and Elisa Lorenzo García for their comments that led to this remark.
Remark 3.12. (Jacobians among PPAVs)
We again take the view that conjecture 3.4 should be a shadow of a (possibly sharper) statement for the family of PPAVs of a given dimension. From this point of view, it is important to note that—asymptotically—100% of PPAVs of dimension 2 are Jacobians (those that are not are either products of PPAVs of lower dimension or Weil restrictions of elliptic curves). Thus, for g = 2, the two conjectures that one can formulate (for curves of genus 2 and principally polarized abelian surfaces) are equivalent. For g = 3, 100% of PPAVs are either Jacobians or quadratic twists of Jacobians (this is explained by the so-called Serre obstruction, see, e.g., Serre’s appendix to [Reference Lauter38]), so conjectures 3.4 and 3.7 for g = 3 are still closely related. As the dimension grows, conjecture 3.4 can be interpreted as saying that Jacobians are ‘typical’ among PPAVs—the distribution of the trace on the subfamily of Jacobians is the same as the distribution among all PPAVs. While we believe that conjecture 3.4 holds for all genera g, we should point out that it is very hard to get numerical evidence when the genus/dimension is 4 or more. This is precisely the threshold above which the difference between PPAVs that are geometrically Jacobians and general PPAVs becomes (asymptotically) relevant, so it would be interesting to study this regime more closely. See figure 5 for an example in which we show the difference between taking into account only Jacobians or all PPAVs.
Remark 3.13. (Principally polarized abelian surfaces with trace zero)
In dimension 2, PPAVs that are not Jacobians are either products of elliptic curves (with the product polarization) or Weil restrictions of elliptic curves defined over a quadratic extension. In particular, over the finite field with q elements, there are ![]() $\gg q^2$ abelian surfaces that are Weil restrictions of elliptic curves defined over
$\gg q^2$ abelian surfaces that are Weil restrictions of elliptic curves defined over ![]() $\mathbb{F}_{q^2}$, but not over
$\mathbb{F}_{q^2}$, but not over ![]() $\mathbb{F}_q$. The Galois representation attached to
$\mathbb{F}_q$. The Galois representation attached to  $A := \operatorname{Res}_{\mathbb{F}_{q^2}/\mathbb{F}_q}(E)$ is the induction from
$A := \operatorname{Res}_{\mathbb{F}_{q^2}/\mathbb{F}_q}(E)$ is the induction from  $\operatorname{Gal}(\overline{\mathbb{F}_q} / \mathbb{F}_{q^2})$ to
$\operatorname{Gal}(\overline{\mathbb{F}_q} / \mathbb{F}_{q^2})$ to ![]() $\operatorname{Gal}\left(\overline{\mathbb{F}_q}/\mathbb{F}_q \right)$ of the representation attached to
$\operatorname{Gal}\left(\overline{\mathbb{F}_q}/\mathbb{F}_q \right)$ of the representation attached to  $E/\mathbb{F}_{q^2}$, which implies that the Frobenius trace of A is zero for any such Weil restriction. Since the total number of genus-2 curves over
$E/\mathbb{F}_{q^2}$, which implies that the Frobenius trace of A is zero for any such Weil restriction. Since the total number of genus-2 curves over ![]() $\mathbb{F}_q$ is of order q 3 (see lemma 2.5), we expect that the proportion of PP abelian surfaces with trace 0 should be significantly higher than the proportion of genus-2 curves with trace 0 (both the number of genus-2 curves and the number of PP abelian surfaces is
$\mathbb{F}_q$ is of order q 3 (see lemma 2.5), we expect that the proportion of PP abelian surfaces with trace 0 should be significantly higher than the proportion of genus-2 curves with trace 0 (both the number of genus-2 curves and the number of PP abelian surfaces is ![]() $\approx q^3$. The number of PP abelian surfaces with trace 0 is
$\approx q^3$. The number of PP abelian surfaces with trace 0 is ![]() $\gg q^2$ more than the corresponding number of curves. In particular, we expect the proportion of PP abelian surfaces of trace 0 to be
$\gg q^2$ more than the corresponding number of curves. In particular, we expect the proportion of PP abelian surfaces of trace 0 to be ![]() $\gg 1/q$ more than the corresponding proportion of curves). If we interpret conjecture 3.4 as a prediction for the distribution of the number of points of PPAVs, this helps in explaining the peak at 0 in figure 5 (this peak is particularly noticeable since for q = 37 the quantity
$\gg 1/q$ more than the corresponding proportion of curves). If we interpret conjecture 3.4 as a prediction for the distribution of the number of points of PPAVs, this helps in explaining the peak at 0 in figure 5 (this peak is particularly noticeable since for q = 37 the quantity ![]() $1/q$ is not at all negligible). Similar comments apply in higher dimensions, but the proportion of PPAVs having trace zero for geometric reasons becomes less significant as the dimension increases.
$1/q$ is not at all negligible). Similar comments apply in higher dimensions, but the proportion of PPAVs having trace zero for geometric reasons becomes less significant as the dimension increases.
Remark 3.14. (Lift to  $\mathbb{Z}_\ell$)
$\mathbb{Z}_\ell$)
Equation (7) requires that we only count those matrices  $M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ with trace t and multiplier q that lift to a matrix
$M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})$ with trace t and multiplier q that lift to a matrix ![]() $\tilde{M} \in X_t^q(\mathbb{Z}_\ell)$. While this condition is natural in our setting (since Frobenius is in fact represented by an
$\tilde{M} \in X_t^q(\mathbb{Z}_\ell)$. While this condition is natural in our setting (since Frobenius is in fact represented by an ![]() $\ell$-adic matrix with the given trace and multiplier), we believe that omitting this condition should lead to the same result, that is, we conjecture that
$\ell$-adic matrix with the given trace and multiplier), we believe that omitting this condition should lead to the same result, that is, we conjecture that
 \begin{equation*}
\tilde{\nu}_\ell(q,t) := \lim_{k \to \infty} \frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) : \operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}
\end{equation*}
\begin{equation*}
\tilde{\nu}_\ell(q,t) := \lim_{k \to \infty} \frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) : \operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}
\end{equation*} coincides with ![]() $\nu_\ell(q,t)$. It is not hard to check that this holds for g = 1, but we have been unable to prove the result in general. The difficulties that arise lie in understanding the singularities of the variety
$\nu_\ell(q,t)$. It is not hard to check that this holds for g = 1, but we have been unable to prove the result in general. The difficulties that arise lie in understanding the singularities of the variety ![]() $X_t^q$, that is, the
$X_t^q$, that is, the ![]() $\mathbb{Z}_\ell$-subscheme of
$\mathbb{Z}_\ell$-subscheme of  $\operatorname{GSp}_{2g, \mathbb{Z}_\ell}^{m}$ defined by the equation
$\operatorname{GSp}_{2g, \mathbb{Z}_\ell}^{m}$ defined by the equation ![]() $\operatorname{Tr}(M)=t$. When
$\operatorname{Tr}(M)=t$. When ![]() $X_t^q$ is smooth over
$X_t^q$ is smooth over ![]() $\mathbb{Z}_\ell$, an application of Hensel’s lemma shows that
$\mathbb{Z}_\ell$, an application of Hensel’s lemma shows that ![]() $\nu_\ell(q,t)$ and
$\nu_\ell(q,t)$ and ![]() $\tilde{\nu}_\ell(q,t)$ both coincide with
$\tilde{\nu}_\ell(q,t)$ both coincide with
 \begin{equation*}
\frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{F}_\ell) : \operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell) / (\ell\varphi(\ell))}.
\end{equation*}
\begin{equation*}
\frac{\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{F}_\ell) : \operatorname{tr}(M)=t, \operatorname{mult}(M)=q \right\} }{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell) / (\ell\varphi(\ell))}.
\end{equation*} Note that, without any information on the singularities of a variety ![]() $X/\mathbb{Z}_\ell$, it is very hard to control the point-counts
$X/\mathbb{Z}_\ell$, it is very hard to control the point-counts ![]() $\#X(\mathbb{Z}/\ell^n\mathbb{Z})$: for example, for the reduced variety defined by the equation
$\#X(\mathbb{Z}/\ell^n\mathbb{Z})$: for example, for the reduced variety defined by the equation ![]() $x^4=\ell y^4$ in the affine plane, we have
$x^4=\ell y^4$ in the affine plane, we have ![]() $\dim X = 1$ and
$\dim X = 1$ and ![]() $\#X(\mathbb{Z}/\ell^n\mathbb{Z}) \gg \ell^{3/2n}$, with the point-count dominated by the singular points with
$\#X(\mathbb{Z}/\ell^n\mathbb{Z}) \gg \ell^{3/2n}$, with the point-count dominated by the singular points with ![]() $x \equiv y \equiv 0\ (\mathrm{mod}\ {\ell^{n/4}})$. Without control on the singularities of X, it seems to us that no version of Hensel’s lemma can be applied to understand the ratio
$x \equiv y \equiv 0\ (\mathrm{mod}\ {\ell^{n/4}})$. Without control on the singularities of X, it seems to us that no version of Hensel’s lemma can be applied to understand the ratio ![]() $\#X(\mathbb{Z}/\ell^n\mathbb{Z}) / \ell^{n \dim X}$ as
$\#X(\mathbb{Z}/\ell^n\mathbb{Z}) / \ell^{n \dim X}$ as ![]() $n \to \infty$.
$n \to \infty$.
Remark 3.15. (Comparison to other recent work)
The recent preprint [Reference Shmakov49] relates the moments
 \begin{equation*}
M_n(g, q) = \mathbb{E}_{\mathbb{P}^{\operatorname{intr}}_{g, q}}[ \#A(\mathbb{F}_q)^n]
\end{equation*}
\begin{equation*}
M_n(g, q) = \mathbb{E}_{\mathbb{P}^{\operatorname{intr}}_{g, q}}[ \#A(\mathbb{F}_q)^n]
\end{equation*} of the random variable ‘number of rational points of A’ (here A is drawn at random from ![]() $\mathcal{A}_g(\mathbb{F}_q)$ using a suitable intrinsic measure) to the higher cohomology of certain moduli spaces, see [Reference Shmakov49, p. 2]. This yields explicit formulas for these moments for small g and n [Reference Shmakov49, corollaries 4.3 and 5.4] and it would be interesting to compare these results with the predictions of conjecture 3.4. It may be possible to carry out this comparison by using the techniques of [Reference Achter, Altuğ, Garcia and Gordon3, Reference Achter and Gordon5].
$\mathcal{A}_g(\mathbb{F}_q)$ using a suitable intrinsic measure) to the higher cohomology of certain moduli spaces, see [Reference Shmakov49, p. 2]. This yields explicit formulas for these moments for small g and n [Reference Shmakov49, corollaries 4.3 and 5.4] and it would be interesting to compare these results with the predictions of conjecture 3.4. It may be possible to carry out this comparison by using the techniques of [Reference Achter, Altuğ, Garcia and Gordon3, Reference Achter and Gordon5].
In particular, [Reference Achter, Altuğ, Garcia and Gordon3, theorem A] comes near to proving conjecture 3.4 in the context of PPAVs. However, we point out that to establish conjecture 3.4 one would still need to overcome several obstacles: the formula of [Reference Achter, Altuğ, Garcia and Gordon3, theorem A] only applies to certain isogeny classes of abelian varieties and involves Tamagawa numbers that would have to be averaged; even more substantially, it is not clear how one would isolate Jacobians among all abelian varieties. Finally, even though this is perhaps only a technical problem, the existence of the limits (7) and (8) seems substantially easier to prove in the context of [Reference Achter, Altuğ, Garcia and Gordon3, theorem A] than it is in the general case we consider here (essentially because in the setting of [Reference Achter, Altuğ, Garcia and Gordon3, theorem A] the expression appearing under the limit sign in (7) is constant for ![]() $k \gg 0$, which is not necessarily true in our generality).
$k \gg 0$, which is not necessarily true in our generality).
3.2. Numerical evidence
In this section, we report on numerical experiments that seem to support conjecture 3.4. The data are computed using MAGMA [Reference Bosma, Cannon and Playoust11]. All the MAGMA scripts to verify our data are available online [Reference Ballini, Lombardo and Verzobio7].
In the graphs below (see figures 1, 2, 3, 4, 5), we plot the distribution ![]() $t \mapsto H'(q,t)$ for various values of g and q. These distributions are obtained by directly counting all isomorphism classes of curves of the given genus over the given finite field (the data for
$t \mapsto H'(q,t)$ for various values of g and q. These distributions are obtained by directly counting all isomorphism classes of curves of the given genus over the given finite field (the data for ![]() $q=53, g=3$ are taken from [Reference Lercier, Ritzenthaler, Rovetta and Sijsling40]). In addition, on the same graphs, we also plot an approximation of the Sato–Tate density and of
$q=53, g=3$ are taken from [Reference Lercier, Ritzenthaler, Rovetta and Sijsling40]). In addition, on the same graphs, we also plot an approximation of the Sato–Tate density and of ![]() $\nu^{\prime}(q,t)$. We briefly explain how we obtain these approximations, starting with a general technique to compute the Sato–Tate density in arbitrary dimension.
$\nu^{\prime}(q,t)$. We briefly explain how we obtain these approximations, starting with a general technique to compute the Sato–Tate density in arbitrary dimension.
Remark 3.16. (Computation of  $\operatorname{ST}_g(x)$ for arbitrary g)
$\operatorname{ST}_g(x)$ for arbitrary g)
For general g, the density ![]() $\operatorname{ST}_g(x)$ can be calculated up to arbitrary precision by using a technique due to Kedlaya-Sutherland [Reference Kedlaya and Sutherland31] and Lachaud [Reference Lachaud34]. One can first use [Reference Kedlaya and Sutherland31, Section 4.1] to compute the moments of
$\operatorname{ST}_g(x)$ can be calculated up to arbitrary precision by using a technique due to Kedlaya-Sutherland [Reference Kedlaya and Sutherland31] and Lachaud [Reference Lachaud34]. One can first use [Reference Kedlaya and Sutherland31, Section 4.1] to compute the moments of ![]() $\operatorname{ST}_g$, that is,
$\operatorname{ST}_g$, that is,
 \begin{equation*}
m_n = \int_{-2g}^{2g} x^n \, d\operatorname{ST}_g(x).
\end{equation*}
\begin{equation*}
m_n = \int_{-2g}^{2g} x^n \, d\operatorname{ST}_g(x).
\end{equation*} Once the moments (or at least, sufficiently many moments) are known, we can recover ![]() $\operatorname{ST}_g(x)$ as follows. Let
$\operatorname{ST}_g(x)$ as follows. Let ![]() $L_n(x)$ be the Legendre polynomials, which form a complete orthogonal basis of
$L_n(x)$ be the Legendre polynomials, which form a complete orthogonal basis of ![]() $L^2([-1, 1])$. By rescaling, the polynomials
$L^2([-1, 1])$. By rescaling, the polynomials
 \begin{equation*}\tilde{L}_n(x) := \left(\int_{-2g}^{2g} L_n(x/2g)^2 \right)^{-1/2}L_n(x/2g)\end{equation*}
\begin{equation*}\tilde{L}_n(x) := \left(\int_{-2g}^{2g} L_n(x/2g)^2 \right)^{-1/2}L_n(x/2g)\end{equation*} form an orthonormal basis of ![]() $L^2([-2g, 2g])$. From the explicit expression of
$L^2([-2g, 2g])$. From the explicit expression of  $\tilde{L}_n(x) = \sum_{i=0}^n a_{n, i}x^i$ as a polynomial, one can easily compute
$\tilde{L}_n(x) = \sum_{i=0}^n a_{n, i}x^i$ as a polynomial, one can easily compute
 \begin{equation*}c_n = \int_{-2g}^{2g} \tilde{L}_n(x) \, d\operatorname{ST}_g(x) = \sum_{i=0}^n a_{n, i}m_i.\end{equation*}
\begin{equation*}c_n = \int_{-2g}^{2g} \tilde{L}_n(x) \, d\operatorname{ST}_g(x) = \sum_{i=0}^n a_{n, i}m_i.\end{equation*} Finally, we have the convergent expansion in ![]() $L^2([-2g, 2g])$
$L^2([-2g, 2g])$
 \begin{equation}
\operatorname{ST}_g(x) = \sum_{n \geq 0} c_n \tilde{L}_n(x),
\end{equation}
\begin{equation}
\operatorname{ST}_g(x) = \sum_{n \geq 0} c_n \tilde{L}_n(x),
\end{equation} which allows the computation of ![]() $\operatorname{ST}_g(x)$ to arbitrary precision. In our numerical experiments, we use this technique to approximate
$\operatorname{ST}_g(x)$ to arbitrary precision. In our numerical experiments, we use this technique to approximate ![]() $\operatorname{ST}_3(x)$.
$\operatorname{ST}_3(x)$.

Figure 1. Case g = 2 and q = 1009. The red dots are the values of Hʹ. The black stars are the values of the approximation of ![]() $\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case,
$\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case, ![]() $d(H',\nu')\approx0.00439$ and
$d(H',\nu')\approx0.00439$ and ![]() $d(H',\nu_\infty)\approx 0.15528$.
$d(H',\nu_\infty)\approx 0.15528$.

Figure 2. Case g = 2 and q = 101. The red dots are the values of Hʹ. The black stars are the values of the approximation of ![]() $\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case,
$\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case, ![]() $d(H',\nu')\approx 0.01117$ and
$d(H',\nu')\approx 0.01117$ and ![]() $d(H',\nu_\infty)\approx 0.15166$.
$d(H',\nu_\infty)\approx 0.15166$.

Figure 3. Case g = 3 and q = 53. The red dots are the values of Hʹ. The black stars are the values of the approximation of ![]() $\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case,
$\nu^{\prime}(q,t)$. The blue graph is the approximation of the Sato–Tate density. In this case, ![]() $d(H',\nu')\approx0.03842$ and
$d(H',\nu')\approx0.03842$ and ![]() $d(H',\nu_\infty)\approx0.03940$.
$d(H',\nu_\infty)\approx0.03940$.

Figure 4. Case g = 2 and q = 5. As pointed out in remark 3.9, there is an issue when ![]() $q+1-t \lt 0$ (for example when t = 7). Indeed,
$q+1-t \lt 0$ (for example when t = 7). Indeed, ![]() $H'(q, 7)=0$ because
$H'(q, 7)=0$ because ![]() $q+1-t$ represents the number of
$q+1-t$ represents the number of ![]() $\mathbb{F}_q$-rational points of a curve. Instead, both
$\mathbb{F}_q$-rational points of a curve. Instead, both ![]() $\nu^{\prime}(q,7)\approx0.0009$ and
$\nu^{\prime}(q,7)\approx0.0009$ and ![]() $\nu_\infty(q,7)\approx0.0011$ are strictly positive.
$\nu_\infty(q,7)\approx0.0011$ are strictly positive.

Figure 5. This graph shows the difference between considering all PPAVs or only Jacobians of curves (see remark 3.12). We take g = 2 and q = 37. We plot in red the distribution Hʹ and in black (an approximation of) the distribution ![]() $\nu^{\prime}(q, t)$. The green dots represent the probabilities of the various traces when we take into account all principally polarized abelian surfaces over
$\nu^{\prime}(q, t)$. The green dots represent the probabilities of the various traces when we take into account all principally polarized abelian surfaces over ![]() $\mathbb{F}_q$. Call this distribution
$\mathbb{F}_q$. Call this distribution ![]() $H'^{\prime}$. The distance between the distributions Hʹ and
$H'^{\prime}$. The distance between the distributions Hʹ and ![]() $\nu^{\prime}(q, t)$ is ≈ 0.02673. The distance between
$\nu^{\prime}(q, t)$ is ≈ 0.02673. The distance between ![]() $H'^{\prime}$ and
$H'^{\prime}$ and ![]() $\nu^{\prime}(q, t)$ is ≈ 0.00777. Note in particular the considerable difference between the data at t = 0, where the inclusion of all PPAVs gives a much better agreement with our prediction. An explanation for this phenomenon is given in remark 3.13.
$\nu^{\prime}(q, t)$ is ≈ 0.00777. Note in particular the considerable difference between the data at t = 0, where the inclusion of all PPAVs gives a much better agreement with our prediction. An explanation for this phenomenon is given in remark 3.13.
In our numerical experiments, we approximate the Sato–Tate density with the value of the series in Eq. (17) truncated at ![]() $n\leq 100$. For
$n\leq 100$. For ![]() $\nu^{\prime}(q,t)$, we approximate the value of
$\nu^{\prime}(q,t)$, we approximate the value of ![]() $\nu(q,t)$ (see Eq. (9)) by considering the product of
$\nu(q,t)$ (see Eq. (9)) by considering the product of ![]() $\nu_\ell(q,t)$ for
$\nu_\ell(q,t)$ for ![]() $\ell\leq 100$ and
$\ell\leq 100$ and ![]() $\ell=\infty$. To compute an approximation of
$\ell=\infty$. To compute an approximation of ![]() $\nu_\ell(q,t)$ for
$\nu_\ell(q,t)$ for ![]() $\ell$ prime, we compute the value of the expression appearing under the limit sign in Eq. (7) for k = 1 or 2. To compute an approximation of
$\ell$ prime, we compute the value of the expression appearing under the limit sign in Eq. (7) for k = 1 or 2. To compute an approximation of ![]() $\nu_\infty(q,t)$, we use our approximation of the Sato–Tate density.
$\nu_\infty(q,t)$, we use our approximation of the Sato–Tate density.
Let
 \begin{equation*}H_{\operatorname{intr}}'(q,t)= \mathbb{P}^{\operatorname{intr}}_{g, q} \left( \{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) = t\} \right).\end{equation*}
\begin{equation*}H_{\operatorname{intr}}'(q,t)= \mathbb{P}^{\operatorname{intr}}_{g, q} \left( \{C \in \mathcal{M}_g(\mathbb{F}_q) : \operatorname{Tr}(C) = t\} \right).\end{equation*} We compute the value of ![]() $H_{\operatorname{intr}}'(q,t)$ by direct enumeration of all the curves of genus g defined over
$H_{\operatorname{intr}}'(q,t)$ by direct enumeration of all the curves of genus g defined over ![]() $\mathbb{F}_q$.
$\mathbb{F}_q$.
Finally, below each graph, we also give the distance d between the measures ![]() $H' := H^{\prime}_{\operatorname{intr}}(q, \cdot)$ and
$H' := H^{\prime}_{\operatorname{intr}}(q, \cdot)$ and ![]() $\nu' := \nu'(q, \cdot)$, as well as the distance between Hʹ and the Sato–Tate measure. Our conjecture predicts that
$\nu' := \nu'(q, \cdot)$, as well as the distance between Hʹ and the Sato–Tate measure. Our conjecture predicts that ![]() $d(H',\nu')$ should go to 0 as q goes to infinity. As a consequence of [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1],
$d(H',\nu')$ should go to 0 as q goes to infinity. As a consequence of [Reference Bergström, Howe, Lorenzo García and Ritzenthaler9, conjecture 5.1], ![]() $d(H',\nu_\infty)$ should go to 0. We proved in proposition 3.6 that the conjecture does not hold.
$d(H',\nu_\infty)$ should go to 0. We proved in proposition 3.6 that the conjecture does not hold.
4. Well-posedness of Eq. (9)
In this section, we prove that the quantity ![]() $\nu(q,t)$ is well defined. We have already observed (remark 3.2) that
$\nu(q,t)$ is well defined. We have already observed (remark 3.2) that ![]() $\nu_{\ell}(q, t)$ is well defined for all
$\nu_{\ell}(q, t)$ is well defined for all ![]() $\ell \leq \infty$, so it suffices to show that, as
$\ell \leq \infty$, so it suffices to show that, as ![]() $\ell \to \infty$ among the prime numbers, we have
$\ell \to \infty$ among the prime numbers, we have ![]() $\nu_{\ell}(q, t)=1+O(\ell^{-2})$. This suffices to ensure that the product (9) converges.
$\nu_{\ell}(q, t)=1+O(\ell^{-2})$. This suffices to ensure that the product (9) converges.
As a preparation for the proof, we introduce the following notation and make some remarks.
Notation 4.1
Let R be a (commutative unitary) ring and let ![]() $m \in R^\times$ be a fixed element. We define
$m \in R^\times$ be a fixed element. We define ![]() $\operatorname{GSp}_{2g, R}^{m}$ as the subscheme of
$\operatorname{GSp}_{2g, R}^{m}$ as the subscheme of ![]() $\operatorname{GSp}_{2g, R}$ cut by the equation
$\operatorname{GSp}_{2g, R}$ cut by the equation ![]() $\operatorname{mult}(M)=m$.
$\operatorname{mult}(M)=m$.
Remark 4.2. Let us fix the antisymmetric form  $\begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}$. The matrix
$\begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}$. The matrix
 \begin{equation*}
M_m := \begin{pmatrix}
m \\
& \ddots \\
&& m \\
&&& 1 \\
&&&& \ddots \\
&&&&& 1
\end{pmatrix}
\end{equation*}
\begin{equation*}
M_m := \begin{pmatrix}
m \\
& \ddots \\
&& m \\
&&& 1 \\
&&&& \ddots \\
&&&&& 1
\end{pmatrix}
\end{equation*} is in ![]() $\operatorname{GSp}_{2g}(R)$ and has multiplier m. Multiplication by Mm gives an algebraic isomorphism between the R-schemes
$\operatorname{GSp}_{2g}(R)$ and has multiplier m. Multiplication by Mm gives an algebraic isomorphism between the R-schemes ![]() $\operatorname{Sp}_{2g, R}$ and
$\operatorname{Sp}_{2g, R}$ and ![]() $\operatorname{GSp}_{2g, R}^{m}$. The same applies for any matrix
$\operatorname{GSp}_{2g, R}^{m}$. The same applies for any matrix ![]() $M_m \in \operatorname{GSp}_{2g}(R)$ with multiplier m. In particular,
$M_m \in \operatorname{GSp}_{2g}(R)$ with multiplier m. In particular, ![]() $\operatorname{GSp}_{2g, R}^{m}$ is smooth for any value of m. If R is a field, the dimension of
$\operatorname{GSp}_{2g, R}^{m}$ is smooth for any value of m. If R is a field, the dimension of ![]() $\operatorname{GSp}_{2g, R}^{m}$ is equal to
$\operatorname{GSp}_{2g, R}^{m}$ is equal to ![]() $\dim \operatorname{Sp}_{2g, R}$.
$\dim \operatorname{Sp}_{2g, R}$.
In what follows we will be interested in the subschemes of ![]() $\operatorname{GSp}_{2g, R}^{m}$ defined by the equation
$\operatorname{GSp}_{2g, R}^{m}$ defined by the equation ![]() $\operatorname{Tr}(M)=t$ for a fixed value of
$\operatorname{Tr}(M)=t$ for a fixed value of ![]() $t \in R$. We will mostly work with
$t \in R$. We will mostly work with ![]() $R=\mathbb{Z}_\ell$ and
$R=\mathbb{Z}_\ell$ and ![]() $R=\mathbb{F}_\ell$.
$R=\mathbb{F}_\ell$.
Definition 4.3. For ![]() $m \in R^\times, t \in R$, we define the R-scheme
$m \in R^\times, t \in R$, we define the R-scheme ![]() $X^m_t$ as the subscheme of
$X^m_t$ as the subscheme of ![]() $\operatorname{GSp}_{2g, R}^{m}$ defined by the equation
$\operatorname{GSp}_{2g, R}^{m}$ defined by the equation ![]() $\operatorname{Tr}(M)=t$.
$\operatorname{Tr}(M)=t$.
Notice that, if we fix ![]() $m \in \mathbb{Z} \setminus \{0\}$, then m is invertible in
$m \in \mathbb{Z} \setminus \{0\}$, then m is invertible in ![]() $\mathbb{Z}[1/m]$, and hence
$\mathbb{Z}[1/m]$, and hence ![]() $X_t^m$ makes sense as a scheme over
$X_t^m$ makes sense as a scheme over ![]() $\operatorname{Spec} \mathbb{Z}[1/m]$. We will be able to reduce this scheme modulo any prime that does not divide m.
$\operatorname{Spec} \mathbb{Z}[1/m]$. We will be able to reduce this scheme modulo any prime that does not divide m.
4.1. Number of points of  $X^m_t$ over finite fields
$X^m_t$ over finite fields
In this section, we study the number of ![]() $\mathbb{F}_\ell$-points of
$\mathbb{F}_\ell$-points of ![]() $X_m^t$ (theorem 4.4 and lemma 4.5) and show that a large proportion of them correspond to smooth points of
$X_m^t$ (theorem 4.4 and lemma 4.5) and show that a large proportion of them correspond to smooth points of ![]() $X_m^t$ (lemma 4.6). For the first objective, our approach is inspired by [Reference Lee39]. More precisely, the main result of [Reference Lee39] gives a formula counting the number of elements in
$X_m^t$ (lemma 4.6). For the first objective, our approach is inspired by [Reference Lee39]. More precisely, the main result of [Reference Lee39] gives a formula counting the number of elements in ![]() $\operatorname{GSp}_{2g}(\mathbb{F}_\ell)$ with given trace and determinant. The same strategy allows us to prove the following version, where we count matrices with given trace and multiplier. Before stating the result, we remind the reader that the q-binomial coefficient
$\operatorname{GSp}_{2g}(\mathbb{F}_\ell)$ with given trace and determinant. The same strategy allows us to prove the following version, where we count matrices with given trace and multiplier. Before stating the result, we remind the reader that the q-binomial coefficient  ${\displaystyle {\begin{bmatrix}n\\r\end{bmatrix}}_{q}}$ is defined as
${\displaystyle {\begin{bmatrix}n\\r\end{bmatrix}}_{q}}$ is defined as  $\prod_{j=0}^{r-1} \frac{q^{n-j}-1}{q^{r-j}-1}$. For ease of comparison with [Reference Lee39], we adopt the same notation as in op. cit.
$\prod_{j=0}^{r-1} \frac{q^{n-j}-1}{q^{r-j}-1}$. For ease of comparison with [Reference Lee39], we adopt the same notation as in op. cit.
Theorem 4.4. Let q be a prime power, ![]() $\zeta \in \mathbb{F}_q^\times$, and
$\zeta \in \mathbb{F}_q^\times$, and ![]() $\eta \in \mathbb{F}_q$. Let
$\eta \in \mathbb{F}_q$. Let
 \begin{equation*}
T_m(\zeta, \eta) = q \sum_{\alpha_1, \ldots, \alpha_m \in \mathbb{F}_q^\times} t\left( \alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} \right) - (q-1)^m,
\end{equation*}
\begin{equation*}
T_m(\zeta, \eta) = q \sum_{\alpha_1, \ldots, \alpha_m \in \mathbb{F}_q^\times} t\left( \alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} \right) - (q-1)^m,
\end{equation*}where
 \begin{equation*}
t(x) = \begin{cases}
1, \text{if }x = \eta \\
0, \text{otherwise},
\end{cases}
\end{equation*}
\begin{equation*}
t(x) = \begin{cases}
1, \text{if }x = \eta \\
0, \text{otherwise},
\end{cases}
\end{equation*}and the sum is regarded as t(0) for m = 0. Let
 \begin{equation*}
C(\zeta, \eta) := \left| \{g \in \operatorname{GSp}_{2n}(\mathbb{F}_q) \bigm\vert \operatorname{mult} g = \zeta, \operatorname{tr} g = \eta \} \right| = \left| X_\eta^\zeta(\mathbb{F}_q) \right|.
\end{equation*}
\begin{equation*}
C(\zeta, \eta) := \left| \{g \in \operatorname{GSp}_{2n}(\mathbb{F}_q) \bigm\vert \operatorname{mult} g = \zeta, \operatorname{tr} g = \eta \} \right| = \left| X_\eta^\zeta(\mathbb{F}_q) \right|.
\end{equation*} We have the following exact formula for ![]() $C(\zeta, \eta)$:
$C(\zeta, \eta)$:
 \begin{equation}
\begin{aligned}
C(\zeta, \eta) = q^{n^2-1}\prod_{j=1}^n\left(q^{2j}-1\right) + E,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
C(\zeta, \eta) = q^{n^2-1}\prod_{j=1}^n\left(q^{2j}-1\right) + E,
\end{aligned}
\end{equation}where
 \begin{align}
E &= q^{n^2-1} \sum_{b=0}^{\lfloor n/2 \rfloor} \left( q^{b^2+b} {\displaystyle {\begin{bmatrix}n\\2b\end{bmatrix}}_{q}} \prod_{j=1}^b (q^{2j-1}-1) \right. \nonumber\\
&\quad \left.\times \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right),
\end{align}
\begin{align}
E &= q^{n^2-1} \sum_{b=0}^{\lfloor n/2 \rfloor} \left( q^{b^2+b} {\displaystyle {\begin{bmatrix}n\\2b\end{bmatrix}}_{q}} \prod_{j=1}^b (q^{2j-1}-1) \right. \nonumber\\
&\quad \left.\times \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right),
\end{align} ![]() $R(m, l)$ denotes
$R(m, l)$ denotes
 \begin{equation*}
R(m, l)=\sum_{0 \lt j_1 \lt \cdots \lt j_l \lt m-l} \prod_{\nu=1}^l (q^{m-\nu-j_\nu}-1),
\end{equation*}
\begin{equation*}
R(m, l)=\sum_{0 \lt j_1 \lt \cdots \lt j_l \lt m-l} \prod_{\nu=1}^l (q^{m-\nu-j_\nu}-1),
\end{equation*} and we set by convention ![]() $R(m, 0)=1$.
$R(m, 0)=1$.
Proof. The proof is virtually identical to that of [Reference Lee39, theorem 1]: if one simply replaces every occurrence of det with ![]() $\operatorname{mult}$ in the proof of [Reference Lee39, theorem 1] everything goes through without difficulty. More precisely, let
$\operatorname{mult}$ in the proof of [Reference Lee39, theorem 1] everything goes through without difficulty. More precisely, let
 \begin{equation*}
e(x) = \begin{cases}
1 \,\text{if } x = \zeta, \\
0 \,\text{otherwise}.
\end{cases}
\end{equation*}
\begin{equation*}
e(x) = \begin{cases}
1 \,\text{if } x = \zeta, \\
0 \,\text{otherwise}.
\end{cases}
\end{equation*} Throughout the proof, several instances of ![]() $\det(d_\alpha)=\alpha^n$ are replaced by
$\det(d_\alpha)=\alpha^n$ are replaced by ![]() $\operatorname{mult}(d_\alpha)=\alpha$, where
$\operatorname{mult}(d_\alpha)=\alpha$, where  $d_\alpha = \begin{pmatrix}
\operatorname{Id}_n & 0 \\
0 & \alpha \operatorname{Id}_n
\end{pmatrix}$. In particular, the sums
$d_\alpha = \begin{pmatrix}
\operatorname{Id}_n & 0 \\
0 & \alpha \operatorname{Id}_n
\end{pmatrix}$. In particular, the sums  $\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha^n)$ are replaced by
$\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha^n)$ are replaced by  $\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha)$. In the proof of [Reference Lee39, theorem 1], the sum
$\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha)$. In the proof of [Reference Lee39, theorem 1], the sum  $\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha^n)$ evaluates to the number S of nth roots of ζ in
$\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha^n)$ evaluates to the number S of nth roots of ζ in ![]() $\mathbb{F}_q^\times$; in our case, the sum
$\mathbb{F}_q^\times$; in our case, the sum  $\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha)$ simply evaluates to 1 for all
$\sum_{\alpha \in \mathbb{F}_q^\times} e(\alpha)$ simply evaluates to 1 for all ![]() $\zeta \in \mathbb{F}_q^\times$.
$\zeta \in \mathbb{F}_q^\times$.
We will think of the expression E appearing in Eq. (19) as an error term. We now proceed to bound this error. We work with a fixed value of n: this implies in particular that the number of summands (resp. factors) in the sum (resp. products) appearing in (19) is O(1). We then have the following estimates (where the implicit constants may depend on n, but not on q):
1.
 ${\displaystyle {\begin{bmatrix}n\\r\end{bmatrix}}_{q}} = \prod_{j=0}^{r-1} \frac{q^{n-j}-1}{q^{r-j}-1} \ll \prod_{j=0}^{r-1} \frac{q^{n-j}}{q^{r-j}} = \prod_{j=0}^{r-1} q^{n-r} = q^{nr-r^2}$, and hence in particular
${\displaystyle {\begin{bmatrix}n\\r\end{bmatrix}}_{q}} = \prod_{j=0}^{r-1} \frac{q^{n-j}-1}{q^{r-j}-1} \ll \prod_{j=0}^{r-1} \frac{q^{n-j}}{q^{r-j}} = \prod_{j=0}^{r-1} q^{n-r} = q^{nr-r^2}$, and hence in particular  ${\displaystyle {\begin{bmatrix}n\\2b \end{bmatrix}}_{q}} \ll q^{2bn-4b^2}$.
${\displaystyle {\begin{bmatrix}n\\2b \end{bmatrix}}_{q}} \ll q^{2bn-4b^2}$.2.
 $\prod_{j=1}^b (q^{2j-1}-1) \leq \prod_{j=1}^b q^{2j-1} = q^{\sum_{j=1}^b (2j-1)} = q^{b^2}$.
$\prod_{j=1}^b (q^{2j-1}-1) \leq \prod_{j=1}^b q^{2j-1} = q^{\sum_{j=1}^b (2j-1)} = q^{b^2}$.3. We claim that
 $R(m, l) \ll q^{ml - l(l+1)}$ for
$R(m, l) \ll q^{ml - l(l+1)}$ for  $m\leq n$. To see this, notice that the length of the sum defining
$m\leq n$. To see this, notice that the length of the sum defining  $R(m, l)$ is O(1), so it suffices to estimate the largest summand. (The length of the sum is O(1) because it is bounded by a function of m, and m is bounded in terms of n.) Clearly, the condition
$R(m, l)$ is O(1), so it suffices to estimate the largest summand. (The length of the sum is O(1) because it is bounded by a function of m, and m is bounded in terms of n.) Clearly, the condition  $j_k \gt j_{k-1}$ for
$j_k \gt j_{k-1}$ for  $k=2, \ldots, l$ yields
$k=2, \ldots, l$ yields  $j_\nu \geq \nu$, so
$j_\nu \geq \nu$, so  $q^{m-\nu-j_\nu} \leq q^{m-2\nu}$. We can then estimate
$q^{m-\nu-j_\nu} \leq q^{m-2\nu}$. We can then estimate
 \begin{equation*}
R(m, l) \ll \prod_{\nu=1}^l q^{m-2\nu} = q^{ml-l(l+1)},
\end{equation*}
\begin{equation*}
R(m, l) \ll \prod_{\nu=1}^l q^{m-2\nu} = q^{ml-l(l+1)},
\end{equation*}as claimed.
4. We also claim that
 $|T_m(\zeta, \eta)| \ll q^m$. To show this, we first remark that, for fixed
$|T_m(\zeta, \eta)| \ll q^m$. To show this, we first remark that, for fixed  $\alpha_1, \ldots, \alpha_{m-1} \in \mathbb{F}_q^\times$, the equation
$\alpha_1, \ldots, \alpha_{m-1} \in \mathbb{F}_q^\times$, the equation
 \begin{equation*}
\alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} = \eta
\end{equation*}
\begin{equation*}
\alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} = \eta
\end{equation*}has at most 2 solutions
 $\alpha_m \in \mathbb{F}_q^\times$. We can then rewrite and estimate
$\alpha_m \in \mathbb{F}_q^\times$. We can then rewrite and estimate  $|T_m(\zeta, \eta)|$ as follows:
$|T_m(\zeta, \eta)|$ as follows:
 \begin{align*}
&\big| q \sum_{\alpha_1, \ldots, \alpha_{m-1} \in \mathbb{F}_q^\times} \sum_{\substack{\alpha_m \in \mathbb{F}_q^\times \\ \alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} = \eta}} 1 -(q-1)^m \big| \\ &\leq q \cdot (q-1)^{m-1} \cdot 2 + (q-1)^m \ll q^m,
\end{align*}
\begin{align*}
&\big| q \sum_{\alpha_1, \ldots, \alpha_{m-1} \in \mathbb{F}_q^\times} \sum_{\substack{\alpha_m \in \mathbb{F}_q^\times \\ \alpha_1+\zeta\alpha_1^{-1} + \cdots + \alpha_m+\zeta\alpha_m^{-1} = \eta}} 1 -(q-1)^m \big| \\ &\leq q \cdot (q-1)^{m-1} \cdot 2 + (q-1)^m \ll q^m,
\end{align*}as desired.
We now give an upper bound for the quantity ![]() $|E|$, with E as in Eq. (19). According to our previous estimates,
$|E|$, with E as in Eq. (19). According to our previous estimates,
 \begin{equation*}
\begin{aligned}
\left|\sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| & \ll
\sum_{l=0}^{\lfloor n/2-b \rfloor} q^l q^{(n-2b+1)l - l(l+1)} q^{n-2b-2l} \\
& \ll q^{n-2b} \sum_{l=0}^{\lfloor n/2-b \rfloor} q^{(n-2b-1)l - l^2}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\left|\sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| & \ll
\sum_{l=0}^{\lfloor n/2-b \rfloor} q^l q^{(n-2b+1)l - l(l+1)} q^{n-2b-2l} \\
& \ll q^{n-2b} \sum_{l=0}^{\lfloor n/2-b \rfloor} q^{(n-2b-1)l - l^2}.
\end{aligned}
\end{equation*} Notice again that the length of this sum is O(1), so it suffices to give an upper bound for its largest summand. For a fixed value of b, the exponent ![]() $(n-2b-1)l - l^2$ is maximal for
$(n-2b-1)l - l^2$ is maximal for  $l=\frac{n-2b-1}{2}$ (which might not be an integer, but still provides an upper bound for the value of the exponent). We thus get
$l=\frac{n-2b-1}{2}$ (which might not be an integer, but still provides an upper bound for the value of the exponent). We thus get
 \begin{equation*}
\left| \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| \ll q^{n-2b} q^{\left( \frac{n-2b-1}{2} \right)^2}.
\end{equation*}
\begin{equation*}
\left| \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| \ll q^{n-2b} q^{\left( \frac{n-2b-1}{2} \right)^2}.
\end{equation*}We now consider the expression
 \begin{align*}
&\left|
q^{b^2+b} {\displaystyle {\begin{bmatrix}n\\2b\end{bmatrix}}_{q}} \prod_{j=1}^b (q^{2j-1}-1) \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| \\ & \ll q^{b^2+b} q^{2bn-4b^2} q^{b^2} q^{n-2b} q^{\left( \frac{n-2b-1}{2} \right)^2},
\end{align*}
\begin{align*}
&\left|
q^{b^2+b} {\displaystyle {\begin{bmatrix}n\\2b\end{bmatrix}}_{q}} \prod_{j=1}^b (q^{2j-1}-1) \sum_{l=0}^{\lfloor n/2-b \rfloor} q^l R(n-2b+1,l)T_{n-2b-2l}(\zeta, \eta) \right| \\ & \ll q^{b^2+b} q^{2bn-4b^2} q^{b^2} q^{n-2b} q^{\left( \frac{n-2b-1}{2} \right)^2},
\end{align*} corresponding to a fixed value of b in the sum (19). The exponent of q on the right-hand side is again a quadratic function of b (to be precise, it is given by  $-b^2 + bn + \frac{1}{4}n^2 + \frac{1}{2}n + 1/4$), which is easily seen to achieve its maximum for
$-b^2 + bn + \frac{1}{4}n^2 + \frac{1}{2}n + 1/4$), which is easily seen to achieve its maximum for ![]() $b=n/2$. This maximum value is given by
$b=n/2$. This maximum value is given by  $\frac{1}{2}n^2 + \frac{1}{2}n + \frac{1}{4}$. Thus,
$\frac{1}{2}n^2 + \frac{1}{2}n + \frac{1}{4}$. Thus,  $q^{(1/2)n^2+(1/2)n+1/4}$ is an upper bound for each summand. Keeping once again in mind that the length of the sum is O(1), we have proved that
$q^{(1/2)n^2+(1/2)n+1/4}$ is an upper bound for each summand. Keeping once again in mind that the length of the sum is O(1), we have proved that
 \begin{equation*}|E|\ll q^{n^2-1} q^{\frac12n^2+\frac12n+\frac14} = q^{\frac{3}{2}n^2 + \frac{1}{2}n - \frac{3}{4}}.\end{equation*}
\begin{equation*}|E|\ll q^{n^2-1} q^{\frac12n^2+\frac12n+\frac14} = q^{\frac{3}{2}n^2 + \frac{1}{2}n - \frac{3}{4}}.\end{equation*}We can finally prove:
Lemma 4.5. For all ![]() $g \geq 2$, all primes
$g \geq 2$, all primes ![]() $\ell$, and all m with
$\ell$, and all m with ![]() $(m, \ell)=1$ we have
$(m, \ell)=1$ we have
 \begin{align}
\frac{\#X_t^m(\mathbb{F}_\ell)}{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)/(\ell\varphi(\ell))}&= \frac{\# \{M \in \operatorname{GSp}_{2g}(\mathbb{F}_\ell) : \operatorname{Tr} (M)=t, \operatorname{mult} M = m \} }{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)/(\ell\varphi(\ell))}\\ &= 1+ O(\ell^{-2}),\nonumber
\end{align}
\begin{align}
\frac{\#X_t^m(\mathbb{F}_\ell)}{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)/(\ell\varphi(\ell))}&= \frac{\# \{M \in \operatorname{GSp}_{2g}(\mathbb{F}_\ell) : \operatorname{Tr} (M)=t, \operatorname{mult} M = m \} }{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)/(\ell\varphi(\ell))}\\ &= 1+ O(\ell^{-2}),\nonumber
\end{align}where the constant implicit in the big-O sign depends only on g.
Proof. The numerator of (20) is given by (18) (with n = g, ![]() $q=\ell$,
$q=\ell$, ![]() $\zeta=m$ and
$\zeta=m$ and ![]() $\eta=t$). Note that
$\eta=t$). Note that  $\ell^{g^2-1} \prod_{j=1}^g \left(\ell^{2j}-1 \right)$ is exactly
$\ell^{g^2-1} \prod_{j=1}^g \left(\ell^{2j}-1 \right)$ is exactly  $\frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)}$. Thus, the ratio in (20) is given by
$\frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)}$. Thus, the ratio in (20) is given by
 \begin{equation*}
1 + \frac{E}{\frac{1}{\ell(\ell-1)} \#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}.
\end{equation*}
\begin{equation*}
1 + \frac{E}{\frac{1}{\ell(\ell-1)} \#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}.
\end{equation*}Since
 \begin{align*}
\frac{1}{\ell(\ell-1)} \#\operatorname{GSp}_{2g}(\mathbb{F}_\ell) = \frac{1}{\ell(\ell-1)} (\ell-1) \#\operatorname{Sp}_{2g}(\mathbb{F}_\ell) = \ell^{g^2-1} \prod_{j=1}^g(\ell^{2j}-1) \gg \ell^{2g^2+g-1},
\end{align*}
\begin{align*}
\frac{1}{\ell(\ell-1)} \#\operatorname{GSp}_{2g}(\mathbb{F}_\ell) = \frac{1}{\ell(\ell-1)} (\ell-1) \#\operatorname{Sp}_{2g}(\mathbb{F}_\ell) = \ell^{g^2-1} \prod_{j=1}^g(\ell^{2j}-1) \gg \ell^{2g^2+g-1},
\end{align*}we obtain that (20) is
 \begin{equation*}
1+O\left( \ell^{\frac{3}{2}g^2 + \frac{1}{2}g -\frac{3}{4} - (2g^2+g-1)} \right) = 1+O\left( \ell^{-\frac{1}{2}g^2 - \frac{1}{2}g +\frac{1}{4}} \right),
\end{equation*}
\begin{equation*}
1+O\left( \ell^{\frac{3}{2}g^2 + \frac{1}{2}g -\frac{3}{4} - (2g^2+g-1)} \right) = 1+O\left( \ell^{-\frac{1}{2}g^2 - \frac{1}{2}g +\frac{1}{4}} \right),
\end{equation*} which is ![]() $1+O(\ell^{-2})$ for all
$1+O(\ell^{-2})$ for all ![]() $g \geq 2$.
$g \geq 2$.
Lemma 4.6. Fix ![]() $t, m \in \mathbb{Z}$ and let
$t, m \in \mathbb{Z}$ and let ![]() $\ell \geq 3$ be a prime number not dividing m. Let
$\ell \geq 3$ be a prime number not dividing m. Let
 \begin{equation*}
X := (X_t^m)_{\mathbb{F}_\ell} = \operatorname{GSp}_{2g, \mathbb{F}_\ell} \cap \{\operatorname{Tr} = t\} \cap \{\operatorname{mult} = m\},
\end{equation*}
\begin{equation*}
X := (X_t^m)_{\mathbb{F}_\ell} = \operatorname{GSp}_{2g, \mathbb{F}_\ell} \cap \{\operatorname{Tr} = t\} \cap \{\operatorname{mult} = m\},
\end{equation*} considered as a variety over ![]() $\mathbb{F}_\ell$. Write
$\mathbb{F}_\ell$. Write ![]() $X^{\operatorname{smooth}}$ for the smooth locus of X. The singular locus
$X^{\operatorname{smooth}}$ for the smooth locus of X. The singular locus ![]() $X^{\operatorname{sing}}$ has codimension at least 3 in X. We have
$X^{\operatorname{sing}}$ has codimension at least 3 in X. We have  $\#X^{\operatorname{sing}}(\mathbb{F}_\ell) = O(\ell^{2g^2+g-4})$ and
$\#X^{\operatorname{sing}}(\mathbb{F}_\ell) = O(\ell^{2g^2+g-4})$ and
 \begin{equation*}
\#X^{\operatorname{smooth}}(\mathbb{F}_\ell)=\frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2})).
\end{equation*}
\begin{equation*}
\#X^{\operatorname{smooth}}(\mathbb{F}_\ell)=\frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2})).
\end{equation*} The implied constants depend on t and m, but not on ![]() $\ell$.
$\ell$.
Proof. We view X as a subvariety of the affine space  $\mathbb{A}_{\mathbb{F}_\ell}^{(2g)^2}$, considered as the space of matrices of size
$\mathbb{A}_{\mathbb{F}_\ell}^{(2g)^2}$, considered as the space of matrices of size ![]() $2g \times 2g$. The variety X is the intersection of
$2g \times 2g$. The variety X is the intersection of  $\operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m} \cong \operatorname{Sp}_{2g, \mathbb{F}_\ell}$ with the hyperplane H defined by the condition
$\operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m} \cong \operatorname{Sp}_{2g, \mathbb{F}_\ell}$ with the hyperplane H defined by the condition ![]() $\operatorname{Tr}(M) = t$. The hyperplane section
$\operatorname{Tr}(M) = t$. The hyperplane section  $\operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m} \cap H$ is smooth at a point
$\operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m} \cap H$ is smooth at a point ![]() $x \in X(\overline{\mathbb{F}_\ell})$ unless the (tangent space to the) hyperplane H contains the tangent space of
$x \in X(\overline{\mathbb{F}_\ell})$ unless the (tangent space to the) hyperplane H contains the tangent space of  $\operatorname{GSp}_{2g, \overline{\mathbb{F}_\ell}}^{m}$ at the point x. Take any point
$\operatorname{GSp}_{2g, \overline{\mathbb{F}_\ell}}^{m}$ at the point x. Take any point ![]() $x \in X(\overline{\mathbb{F}_\ell})$. Since x has multiplier m, left multiplication by
$x \in X(\overline{\mathbb{F}_\ell})$. Since x has multiplier m, left multiplication by  $x \in \operatorname{GSp}_{2g}(\overline{\mathbb{F}_\ell})$ gives an isomorphism Lx between
$x \in \operatorname{GSp}_{2g}(\overline{\mathbb{F}_\ell})$ gives an isomorphism Lx between  $\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ and
$\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ and  $\operatorname{GSp}_{2g, \overline{\mathbb{F}_\ell}}^{m}$. The differential of Lx gives an isomorphism between the tangent space at
$\operatorname{GSp}_{2g, \overline{\mathbb{F}_\ell}}^{m}$. The differential of Lx gives an isomorphism between the tangent space at ![]() $\operatorname{Id}$ and the tangent space at x. If we identify both tangent spaces to subspaces of the tangent space to
$\operatorname{Id}$ and the tangent space at x. If we identify both tangent spaces to subspaces of the tangent space to  $\mathbb{A}_{\overline{\mathbb{F}_\ell}}^{(2g)^2}$ (that is, to matrices of size
$\mathbb{A}_{\overline{\mathbb{F}_\ell}}^{(2g)^2}$ (that is, to matrices of size ![]() $2g \times 2g$), the differential in question is simply multiplication by x itself. Thus, we may view the tangent space at x as the image via x of the tangent space at
$2g \times 2g$), the differential in question is simply multiplication by x itself. Thus, we may view the tangent space at x as the image via x of the tangent space at ![]() $\operatorname{Id}$, which is the Lie algebra of
$\operatorname{Id}$, which is the Lie algebra of  $\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$. This can be written down explicitly: choose the anti-symmetric bilinear form represented by the matrix
$\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$. This can be written down explicitly: choose the anti-symmetric bilinear form represented by the matrix
 \begin{equation*}
\Omega := \begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\Omega := \begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}.
\end{equation*} Differentiating the condition ![]() ${}^tM \Omega M = \Omega$, we find that the Lie algebra of
${}^tM \Omega M = \Omega$, we find that the Lie algebra of  $\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ is given by those matrices M that satisfy
$\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ is given by those matrices M that satisfy ![]() ${}^tM\Omega + \Omega M = 0$. Writing M in block form, we obtain that
${}^tM\Omega + \Omega M = 0$. Writing M in block form, we obtain that  $\operatorname{Lie} \operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ is the vector space of
$\operatorname{Lie} \operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}$ is the vector space of ![]() $\overline{\mathbb{F}_\ell}$-matrices
$\overline{\mathbb{F}_\ell}$-matrices
 \begin{equation*}
\begin{pmatrix}
A & B \\ C & D
\end{pmatrix}
\end{equation*}
\begin{equation*}
\begin{pmatrix}
A & B \\ C & D
\end{pmatrix}
\end{equation*} with ![]() ${}^t B= B, {}^tC = C, {}^tD = -A$ (see [Reference Fulton and Harris22, § 16.1] for the identical calculation over the complex numbers). From the previous arguments, it follows that x can only be a singular point if
${}^t B= B, {}^tC = C, {}^tD = -A$ (see [Reference Fulton and Harris22, § 16.1] for the identical calculation over the complex numbers). From the previous arguments, it follows that x can only be a singular point if
 \begin{equation*}
x \operatorname{Lie}(\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}) \subseteq \{\operatorname{Tr} = 0\},
\end{equation*}
\begin{equation*}
x \operatorname{Lie}(\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}) \subseteq \{\operatorname{Tr} = 0\},
\end{equation*}which is to say
 \begin{equation*}
\operatorname{Tr} (xL) = 0 \quad \forall L \in \operatorname{Lie}(\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}).
\end{equation*}
\begin{equation*}
\operatorname{Tr} (xL) = 0 \quad \forall L \in \operatorname{Lie}(\operatorname{Sp}_{2g, \overline{\mathbb{F}_\ell}}).
\end{equation*} Write  $x = \begin{pmatrix}
\alpha & \beta \\ \gamma & \delta
\end{pmatrix}$ and
$x = \begin{pmatrix}
\alpha & \beta \\ \gamma & \delta
\end{pmatrix}$ and  $L=\begin{pmatrix}
A & B \\ C & D
\end{pmatrix}$ with
$L=\begin{pmatrix}
A & B \\ C & D
\end{pmatrix}$ with ![]() $B, C$ symmetric and
$B, C$ symmetric and ![]() $D=-{}^tA$. This easily gives
$D=-{}^tA$. This easily gives ![]() $\operatorname{Tr} (\beta C) = \operatorname{Tr}(\gamma B) = 0$ for all symmetric
$\operatorname{Tr} (\beta C) = \operatorname{Tr}(\gamma B) = 0$ for all symmetric ![]() $B, C$ (which implies that
$B, C$ (which implies that ![]() $\beta, \gamma$ are anti-symmetric) and
$\beta, \gamma$ are anti-symmetric) and
for all A (which implies ![]() $\alpha={}^t\delta$).
$\alpha={}^t\delta$).
Thus, the locus of non-smooth points is contained in the linear space defined by the equations
This linear space has dimension  $g^2 + 2 \frac{g(g-1)}{2} = 2g^2-g$, and hence codimension at least
$g^2 + 2 \frac{g(g-1)}{2} = 2g^2-g$, and hence codimension at least ![]() $2g-1 \geq 3$ in X, each of whose irreducible components has dimension at least
$2g-1 \geq 3$ in X, each of whose irreducible components has dimension at least  $\dim \operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m}-1 = \dim \operatorname{Sp}_{2g, \mathbb{F}_\ell}-1 = 2g^2+g-1$ (at least one irreducible component has exactly this dimension). We now observe that by the Lang–Weil estimates [Reference Lang and Weil37, theorem 1] we have
$\dim \operatorname{GSp}_{2g, \mathbb{F}_\ell}^{m}-1 = \dim \operatorname{Sp}_{2g, \mathbb{F}_\ell}-1 = 2g^2+g-1$ (at least one irreducible component has exactly this dimension). We now observe that by the Lang–Weil estimates [Reference Lang and Weil37, theorem 1] we have  $\#X^{\operatorname{sing}}(\mathbb{F}_\ell) = O( \ell^{\dim X^{\operatorname{sing}}} ) = O(\ell^{\dim X - 3})$, with an implicit constant that depends only on X and not
$\#X^{\operatorname{sing}}(\mathbb{F}_\ell) = O( \ell^{\dim X^{\operatorname{sing}}} ) = O(\ell^{\dim X - 3})$, with an implicit constant that depends only on X and not ![]() $\ell$. Taking into account the obvious decomposition
$\ell$. Taking into account the obvious decomposition ![]() $X^{\operatorname{smooth}}(\mathbb{F}_\ell) \bigsqcup X^{\operatorname{sing}}(\mathbb{F}_\ell) = X(\mathbb{F}_\ell)$ and the fact that
$X^{\operatorname{smooth}}(\mathbb{F}_\ell) \bigsqcup X^{\operatorname{sing}}(\mathbb{F}_\ell) = X(\mathbb{F}_\ell)$ and the fact that  $
\#X(\mathbb{F}_\ell) = \frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2}))
$ by lemma 4.5, we obtain the desired estimate
$
\#X(\mathbb{F}_\ell) = \frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2}))
$ by lemma 4.5, we obtain the desired estimate  $\#X^{\operatorname{smooth}}(\mathbb{F}_\ell) = \frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2})).$
$\#X^{\operatorname{smooth}}(\mathbb{F}_\ell) = \frac{\#\operatorname{GSp}_{2g, \mathbb{F}_\ell}(\mathbb{F}_\ell)}{\ell \varphi(\ell)} (1 + O(\ell^{-2})).$
4.2. Convergence of the infinite product (9)
Lemma 4.7. Let ![]() $g\geq 2$, q be a prime power, and
$g\geq 2$, q be a prime power, and ![]() $t\in \mathbb{Z}$. Let
$t\in \mathbb{Z}$. Let ![]() $\ell\geq 3$ be a prime that does not divide q. We have
$\ell\geq 3$ be a prime that does not divide q. We have ![]() $\nu_{\ell}(q, t)=1+O(\ell^{-2})$, where the implied constant depends on g, q, and t.
$\nu_{\ell}(q, t)=1+O(\ell^{-2})$, where the implied constant depends on g, q, and t.
Proof. Let ![]() $X:=X_t^q$. We apply [Reference Oesterlé44, Property (U), p. 326] to
$X:=X_t^q$. We apply [Reference Oesterlé44, Property (U), p. 326] to
 \begin{equation*}
m=1, \quad N = (2g)^2, \quad n=n, \quad B = x_0 + \ell \mathbb{Z}_\ell^{(2g)^2}
\end{equation*}
\begin{equation*}
m=1, \quad N = (2g)^2, \quad n=n, \quad B = x_0 + \ell \mathbb{Z}_\ell^{(2g)^2}
\end{equation*} where ![]() $x_0 \bmod \ell$ is a matrix lying in
$x_0 \bmod \ell$ is a matrix lying in ![]() $X^{\operatorname{sing}}(\mathbb{F}_\ell)$. We first assume that
$X^{\operatorname{sing}}(\mathbb{F}_\ell)$. We first assume that ![]() $X_{\mathbb{Z}_\ell}$ is irreducible. Considering X as a scheme over the spectrum of the DVR
$X_{\mathbb{Z}_\ell}$ is irreducible. Considering X as a scheme over the spectrum of the DVR ![]() $\mathbb{Z}_\ell$, [1, lemma 0B2J] shows that
$\mathbb{Z}_\ell$, [1, lemma 0B2J] shows that ![]() $X_{\mathbb{F}_\ell}$ is equidimensional of some dimension d, and Oesterlé’s result gives
$X_{\mathbb{F}_\ell}$ is equidimensional of some dimension d, and Oesterlé’s result gives
for a constant C that depends only on the degree in dimension d [Reference Oesterlé44, § 0.6] of ![]() $X_{\mathbb{F}_\ell}$, which is clearly bounded independently of
$X_{\mathbb{F}_\ell}$, which is clearly bounded independently of ![]() $\ell$. On the other hand, we have
$\ell$. On the other hand, we have
 \begin{align*}
&\#\{\text{closed balls A of radius}\ \ell^{-n}: A \cap X \neq \emptyset \,\text{and } A \subseteq B \} \\= &\quad \# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \equiv x_0\ (\mathrm{mod}\ {\ell})
\end{array}
\right\}.
\end{align*}
\begin{align*}
&\#\{\text{closed balls A of radius}\ \ell^{-n}: A \cap X \neq \emptyset \,\text{and } A \subseteq B \} \\= &\quad \# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \equiv x_0\ (\mathrm{mod}\ {\ell})
\end{array}
\right\}.
\end{align*} Hence, summing over the points ![]() $x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)$, we obtain
$x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)$, we obtain
 \begin{equation}
\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \bmod \ell \in X^{\operatorname{sing}}(\mathbb{F}_\ell)
\end{array}
\right\} \leq C \#X^{\operatorname{sing}}(\mathbb{F}_\ell) \ell^{(n-1) \dim X}.
\end{equation}
\begin{equation}
\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \bmod \ell \in X^{\operatorname{sing}}(\mathbb{F}_\ell)
\end{array}
\right\} \leq C \#X^{\operatorname{sing}}(\mathbb{F}_\ell) \ell^{(n-1) \dim X}.
\end{equation} If ![]() $X_{\mathbb{Z}_\ell}$ is not irreducible, we can repeat the above argument with each irreducible component Xi. If Ci is the constant that corresponds to the component Xi, applying the previous argument to Xi and summing over i we obtain
$X_{\mathbb{Z}_\ell}$ is not irreducible, we can repeat the above argument with each irreducible component Xi. If Ci is the constant that corresponds to the component Xi, applying the previous argument to Xi and summing over i we obtain
 \begin{align*}
&\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \bmod \ell \in X^{\operatorname{sing}}(\mathbb{F}_\ell)
\end{array}
\right\} \\
& \leq \left(\sum_i C_i\right)\#X^{\operatorname{sing}}(\mathbb{F}_\ell) \ell^{(n-1) \dim X}.
\end{align*}
\begin{align*}
&\# \left\{M \in \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^n\mathbb{Z}) : \begin{array}{c} \exists \tilde{M} \in X(\mathbb{Z}_\ell) \\ \tilde{M} \equiv M\ (\mathrm{mod}\ {\ell^n}) \\ M \bmod \ell \in X^{\operatorname{sing}}(\mathbb{F}_\ell)
\end{array}
\right\} \\
& \leq \left(\sum_i C_i\right)\#X^{\operatorname{sing}}(\mathbb{F}_\ell) \ell^{(n-1) \dim X}.
\end{align*} Note that the number of irreducible components is bounded independently of ![]() $\ell$, and so is the constant
$\ell$, and so is the constant ![]() $\left(\sum_{i} C_i\right)$ (because the degrees are bounded in terms of the equations of X, which are independent of
$\left(\sum_{i} C_i\right)$ (because the degrees are bounded in terms of the equations of X, which are independent of ![]() $\ell$). The conclusion is that there exists a constant C such that (21) holds for all n and all but finitely many
$\ell$). The conclusion is that there exists a constant C such that (21) holds for all n and all but finitely many ![]() $\ell$.
$\ell$.
Recall now the definition of ![]() $\nu_\ell(q, t)$ from Eq. (7): it is the limit over k of the ratio
$\nu_\ell(q, t)$ from Eq. (7): it is the limit over k of the ratio
 \begin{equation}
\frac{\# \operatorname{Im}\left( X(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}.
\end{equation}
\begin{equation}
\frac{\# \operatorname{Im}\left( X(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) }{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) / (\ell^k\varphi(\ell^k))}.
\end{equation} Clearly, a matrix M counted in the numerator of this expression in particular reduces modulo ![]() $\ell$ to a point in
$\ell$ to a point in ![]() $X(\mathbb{F}_\ell)$. For a fixed
$X(\mathbb{F}_\ell)$. For a fixed ![]() $x_0 \in X(\mathbb{F}_\ell)$, denote by
$x_0 \in X(\mathbb{F}_\ell)$, denote by ![]() $N(x_0, k)$ the quantity
$N(x_0, k)$ the quantity
 \begin{equation*}
N(x_0, k) = \#\left\{
M \in \operatorname{Im}\left( X(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) : M \equiv x_0\ (\mathrm{mod}\ {\ell})
\right\}.
\end{equation*}
\begin{equation*}
N(x_0, k) = \#\left\{
M \in \operatorname{Im}\left( X(\mathbb{Z}_\ell) \to \operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) : M \equiv x_0\ (\mathrm{mod}\ {\ell})
\right\}.
\end{equation*} When x 0 is a smooth point of ![]() $X(\mathbb{F}_\ell)$, Hensel’s lemma shows that x 0 has precisely
$X(\mathbb{F}_\ell)$, Hensel’s lemma shows that x 0 has precisely ![]() $\ell^{(k-1)\dim X_{\mathbb{F}_\ell}}$ lifts to
$\ell^{(k-1)\dim X_{\mathbb{F}_\ell}}$ lifts to ![]() $X(\mathbb{Z}/\ell^k\mathbb{Z})$, and each of these further lifts to a point in
$X(\mathbb{Z}/\ell^k\mathbb{Z})$, and each of these further lifts to a point in ![]() $X(\mathbb{Z}_\ell)$ (note that a smooth point necessarily lies on a component of dimension equal to
$X(\mathbb{Z}_\ell)$ (note that a smooth point necessarily lies on a component of dimension equal to ![]() $\dim X_{\mathbb{F}_\ell}$: indeed, X is a hyperplane section of a smooth variety, so every smooth point lies on a component of maximal dimension). Therefore, we have
$\dim X_{\mathbb{F}_\ell}$: indeed, X is a hyperplane section of a smooth variety, so every smooth point lies on a component of maximal dimension). Therefore, we have  $N(x_0, k)=\ell^{(k-1)\dim X_{\mathbb{F}_\ell}}$ for such x 0. On the other hand, Eq. (21) and lemma 4.6 show that
$N(x_0, k)=\ell^{(k-1)\dim X_{\mathbb{F}_\ell}}$ for such x 0. On the other hand, Eq. (21) and lemma 4.6 show that  $\sum_{x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)} N(x_0, k) = O(\ell^{k \dim X_{\mathbb{F}_\ell}-3})$.
$\sum_{x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)} N(x_0, k) = O(\ell^{k \dim X_{\mathbb{F}_\ell}-3})$.
Thus, the numerator of (22) is given by
 \begin{equation*}
\begin{aligned}
\sum_{x_0 \in X(\mathbb{F}_\ell)} N(x_0, k) & = \sum_{x_0 \in X^{\operatorname{smooth}}(\mathbb{F}_\ell)} N(x_0, k) + \sum_{x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)} N(x_0, k) \\
& = \#X^{\operatorname{smooth}}(\mathbb{F}_\ell) \ell^{(k-1)\dim X_{\mathbb{F}_\ell}} + O(\ell^{k \dim X_{\mathbb{F}_\ell}-3}) \\
& = \frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)} (1+O(\ell^{-2})) \cdot \ell^{(k-1)\dim X_{\mathbb{F}_\ell}} + O(\ell^{k \dim X_{\mathbb{F}_\ell}-3}),
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\sum_{x_0 \in X(\mathbb{F}_\ell)} N(x_0, k) & = \sum_{x_0 \in X^{\operatorname{smooth}}(\mathbb{F}_\ell)} N(x_0, k) + \sum_{x_0 \in X^{\operatorname{sing}}(\mathbb{F}_\ell)} N(x_0, k) \\
& = \#X^{\operatorname{smooth}}(\mathbb{F}_\ell) \ell^{(k-1)\dim X_{\mathbb{F}_\ell}} + O(\ell^{k \dim X_{\mathbb{F}_\ell}-3}) \\
& = \frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)} (1+O(\ell^{-2})) \cdot \ell^{(k-1)\dim X_{\mathbb{F}_\ell}} + O(\ell^{k \dim X_{\mathbb{F}_\ell}-3}),
\end{aligned}
\end{equation*} where in the last equality we have applied lemma 4.6. Using  $\dim X_{\mathbb{F}_\ell} = \dim \operatorname{GSp}_{2g, \mathbb{F}_\ell} - 2$ and dividing by
$\dim X_{\mathbb{F}_\ell} = \dim \operatorname{GSp}_{2g, \mathbb{F}_\ell} - 2$ and dividing by
 \begin{equation*}
\frac{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})}{\ell^k\varphi(\ell^k)} = \frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)} \ell^{(k-1) \dim X_{\mathbb{F}_\ell}},
\end{equation*}
\begin{equation*}
\frac{\#\operatorname{GSp}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z})}{\ell^k\varphi(\ell^k)} = \frac{\#\operatorname{GSp}_{2g}(\mathbb{F}_\ell)}{\ell\varphi(\ell)} \ell^{(k-1) \dim X_{\mathbb{F}_\ell}},
\end{equation*} we obtain that (22) is ![]() $1+O(\ell^{-2})$. The claim follows upon passing to the limit in k.
$1+O(\ell^{-2})$. The claim follows upon passing to the limit in k.
Theorem 4.8. Let q be a prime power and ![]() $t \in \mathbb{Z}$. The infinite product
$t \in \mathbb{Z}$. The infinite product
 \begin{equation*}\nu(q,t)=\nu_\infty(q, t)\prod_{\ell \lt \infty}\nu_{\ell}(q, t)\end{equation*}
\begin{equation*}\nu(q,t)=\nu_\infty(q, t)\prod_{\ell \lt \infty}\nu_{\ell}(q, t)\end{equation*}converges.
Proof. By lemma 4.7, we have ![]() $\nu_{\ell}(q, t)=1+O(\ell^{-2})$ as
$\nu_{\ell}(q, t)=1+O(\ell^{-2})$ as ![]() $\ell$ ranges over primes
$\ell$ ranges over primes ![]() $\ell \geq 3$ that do not divide q. The factors
$\ell \geq 3$ that do not divide q. The factors ![]() $\nu_\infty(q,t)$,
$\nu_\infty(q,t)$, ![]() $\nu_2(q, t)$ and
$\nu_2(q, t)$ and ![]() $\nu_p(q,t)$ are well defined, as already argued. It follows that the infinite product
$\nu_p(q,t)$ are well defined, as already argued. It follows that the infinite product ![]() $\prod_{\ell \lt \infty}\nu_{\ell}(q, t)$ converges.
$\prod_{\ell \lt \infty}\nu_{\ell}(q, t)$ converges.
We conclude this section by proving that ![]() $\nu(q,t)$ is strictly positive for
$\nu(q,t)$ is strictly positive for ![]() $t \in \mathbb{Z}$ lying in the interval
$t \in \mathbb{Z}$ lying in the interval ![]() $(-2g\sqrt{q},2g\sqrt{q})$. This also proves that the denominator in Eq. (10) is non-zero and that
$(-2g\sqrt{q},2g\sqrt{q})$. This also proves that the denominator in Eq. (10) is non-zero and that ![]() $\nu^{\prime}(q,t)$ is strictly positive for
$\nu^{\prime}(q,t)$ is strictly positive for ![]() $t \in \mathbb{Z}$ lying in the interval
$t \in \mathbb{Z}$ lying in the interval ![]() $(-2g\sqrt{q},2g\sqrt{q})$.
$(-2g\sqrt{q},2g\sqrt{q})$.
Lemma 4.9. Let t be an integer in the open interval ![]() $(-2g\sqrt{q},2g\sqrt{q})$. The quantity
$(-2g\sqrt{q},2g\sqrt{q})$. The quantity ![]() $\nu(q,t)$ is non-zero (hence strictly positive).
$\nu(q,t)$ is non-zero (hence strictly positive).
Proof. Since the infinite product defining ![]() $\nu(q,t)$ converges, it suffices to show that each factor in this product is non-zero. This is well known to be true for the infinite factor
$\nu(q,t)$ converges, it suffices to show that each factor in this product is non-zero. This is well known to be true for the infinite factor ![]() $\nu_\infty(q,t)$, whose support is the interval
$\nu_\infty(q,t)$, whose support is the interval ![]() $[-2g\sqrt{q}, 2g\sqrt{q}]$. To show that
$[-2g\sqrt{q}, 2g\sqrt{q}]$. To show that ![]() $\nu_\ell(q,t)$ is non-zero (including for
$\nu_\ell(q,t)$ is non-zero (including for ![]() $\ell= p$) we proceed as follows. Let
$\ell= p$) we proceed as follows. Let ![]() $X_t^q$ be as in definition 4.3 (for the ring
$X_t^q$ be as in definition 4.3 (for the ring ![]() $R=\mathbb{Q}_\ell$) and let for simplicity
$R=\mathbb{Q}_\ell$) and let for simplicity  $X^q := \operatorname{GSp}_{2g, \mathbb{Q}_\ell}^{q}$. We rewrite the definition of
$X^q := \operatorname{GSp}_{2g, \mathbb{Q}_\ell}^{q}$. We rewrite the definition of ![]() $\nu_\ell(q,t)$ in the form of remark 3.8, namely,
$\nu_\ell(q,t)$ in the form of remark 3.8, namely,
 \begin{equation*}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( X^q(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) / \ell^k}.
\end{equation*}
\begin{equation*}
\nu_{\ell}(q, t) = \lim_{k \to \infty} \frac{\#\operatorname{Im}\left( X^q_t(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right)}{\#\operatorname{Im}\left( X^q(\mathbb{Q}_\ell) \cap \operatorname{Mat}_{2g}(\mathbb{Z}_\ell) \to \operatorname{Mat}_{2g}(\mathbb{Z}/\ell^k\mathbb{Z}) \right) / \ell^k}.
\end{equation*} Set  $d := \dim \operatorname{GSp}_{2g,\mathbb{Q}_\ell}-2 = 2g^2+g-1$ and multiply both numerator and denominator by
$d := \dim \operatorname{GSp}_{2g,\mathbb{Q}_\ell}-2 = 2g^2+g-1$ and multiply both numerator and denominator by ![]() $\ell^{-kd}$. We see both Xq and
$\ell^{-kd}$. We see both Xq and ![]() $X^q_t$ as subschemes of
$X^q_t$ as subschemes of  $\mathbb{A}_{\mathbb{Q}_\ell}^{(2g)^2}$, so that their
$\mathbb{A}_{\mathbb{Q}_\ell}^{(2g)^2}$, so that their ![]() $\mathbb{Q}_\ell$-points are subsets of
$\mathbb{Q}_\ell$-points are subsets of  $\mathbb{Q}_\ell^{(2g)^2}$. Let
$\mathbb{Q}_\ell^{(2g)^2}$. Let  $Y_t^q := X_t^q(\mathbb{Q}_\ell) \cap \mathbb{Z}_\ell^{(2g)^2}$ and
$Y_t^q := X_t^q(\mathbb{Q}_\ell) \cap \mathbb{Z}_\ell^{(2g)^2}$ and  $Y^q := X^q(\mathbb{Q}_\ell) \cap \mathbb{Z}_\ell^{(2g)^2}$. The sets
$Y^q := X^q(\mathbb{Q}_\ell) \cap \mathbb{Z}_\ell^{(2g)^2}$. The sets ![]() $Y_t^q$ and Yq are closed analytic subsets of
$Y_t^q$ and Yq are closed analytic subsets of  $\mathbb{Z}_\ell^{(2g)^2}$. Note that Xq is smooth and irreducible of dimension d + 1, hence
$\mathbb{Z}_\ell^{(2g)^2}$. Note that Xq is smooth and irreducible of dimension d + 1, hence ![]() $X_t^q$—which is a subscheme of Xq defined by a single non-trivial equation—has dimension d: slicing with a hyperplane makes the dimension drop at most by 1; on the other hand, the dimension must drop (if
$X_t^q$—which is a subscheme of Xq defined by a single non-trivial equation—has dimension d: slicing with a hyperplane makes the dimension drop at most by 1; on the other hand, the dimension must drop (if ![]() $X_t^q$ had a component of dimension d + 1, by the irreducibility of Xq we would have
$X_t^q$ had a component of dimension d + 1, by the irreducibility of Xq we would have ![]() $X_t^q \supseteq X^q$, which is not the case). More precisely, by the same argument, every irreducible component of
$X_t^q \supseteq X^q$, which is not the case). More precisely, by the same argument, every irreducible component of ![]() $X_t^q$ has dimension d. We can thus write
$X_t^q$ has dimension d. We can thus write
 \begin{equation}
\nu_\ell(q,t) = \lim_{k \to \infty} \frac{\ell^{-dk} \#\operatorname{Im}(Y_t^q \to (\mathbb{Z}/\ell^k\mathbb{Z})^{(2g)^2})}{\ell^{-(d+1)k} \#\operatorname{Im}(Y^q \to (\mathbb{Z}/\ell^k\mathbb{Z})^{(2g)^2})}.
\end{equation}
\begin{equation}
\nu_\ell(q,t) = \lim_{k \to \infty} \frac{\ell^{-dk} \#\operatorname{Im}(Y_t^q \to (\mathbb{Z}/\ell^k\mathbb{Z})^{(2g)^2})}{\ell^{-(d+1)k} \#\operatorname{Im}(Y^q \to (\mathbb{Z}/\ell^k\mathbb{Z})^{(2g)^2})}.
\end{equation} Recall from [Reference Oesterlé44, § 3] the notion of measure in dimension d of a closed analytic subset Y of  $\mathbb{Z}_\ell^{(2g)^2}$ of dimension
$\mathbb{Z}_\ell^{(2g)^2}$ of dimension ![]() $\leq d$ (denoted by
$\leq d$ (denoted by ![]() $\mu_d(Y)$). By [Reference Oesterlé44, théorème 2], the numerator and denominator of (23) admit limit as
$\mu_d(Y)$). By [Reference Oesterlé44, théorème 2], the numerator and denominator of (23) admit limit as ![]() $k \to \infty$, and these limits are given by
$k \to \infty$, and these limits are given by ![]() $\mu_d(Y_t^q)$ and
$\mu_d(Y_t^q)$ and ![]() $\mu_{d+1}(Y^q)$, respectively. Hence,
$\mu_{d+1}(Y^q)$, respectively. Hence,  $\nu_\ell(q,t) = \frac{\mu_d(Y_t^q)}{\mu_{d+1}(Y^q)}$.
$\nu_\ell(q,t) = \frac{\mu_d(Y_t^q)}{\mu_{d+1}(Y^q)}$.
To conclude, it suffices to show that ![]() $\mu_{d+1}(Y^q)$ and
$\mu_{d+1}(Y^q)$ and ![]() $\mu_d(Y_t^q)$ are both strictly positive. Note that Yq is open in
$\mu_d(Y_t^q)$ are both strictly positive. Note that Yq is open in ![]() $X^q(\mathbb{Q}_\ell)$ for the
$X^q(\mathbb{Q}_\ell)$ for the ![]() $\ell$-adic topology, since it is the intersection of
$\ell$-adic topology, since it is the intersection of ![]() $X^q(\mathbb{Q}_\ell)$ with the
$X^q(\mathbb{Q}_\ell)$ with the ![]() $\ell$-adically open set
$\ell$-adically open set  $(\mathbb{Z}_\ell)^{(2g)^2}$; a similar comment applies to
$(\mathbb{Z}_\ell)^{(2g)^2}$; a similar comment applies to ![]() $X_t^q$. We claim that to check the positivity of
$X_t^q$. We claim that to check the positivity of ![]() $\mu_{d+1}(Y^q)$ and
$\mu_{d+1}(Y^q)$ and ![]() $\mu_d(Y_t^q)$ it suffices to show that
$\mu_d(Y_t^q)$ it suffices to show that ![]() $Y^q, Y_t^q$ contain at least one smooth point of
$Y^q, Y_t^q$ contain at least one smooth point of ![]() $X^q(\mathbb{Q}_\ell), X_t^q(\mathbb{Q}_\ell)$ respectively. To show this implication, we argue as follows (we discuss the case of
$X^q(\mathbb{Q}_\ell), X_t^q(\mathbb{Q}_\ell)$ respectively. To show this implication, we argue as follows (we discuss the case of ![]() $X^q_t$, but the case of Xq is completely analogous, and in fact easier since Xq is smooth). The
$X^q_t$, but the case of Xq is completely analogous, and in fact easier since Xq is smooth). The ![]() $\ell$-adic analytic variety
$\ell$-adic analytic variety ![]() $X^q_t(\mathbb{Q}_\ell)$ is of pure dimension d, and its smooth points
$X^q_t(\mathbb{Q}_\ell)$ is of pure dimension d, and its smooth points ![]() $(X^q_t)_{\operatorname{smooth}}$ form an
$(X^q_t)_{\operatorname{smooth}}$ form an ![]() $\ell$-adically open set, so the intersection
$\ell$-adically open set, so the intersection ![]() $Y^q_t \cap (X^q_t)_{\operatorname{smooth}}$ is
$Y^q_t \cap (X^q_t)_{\operatorname{smooth}}$ is ![]() $\ell$-adically open (recall that
$\ell$-adically open (recall that ![]() $Y^q_t$ is
$Y^q_t$ is ![]() $\ell$-adically open). In particular, if
$\ell$-adically open). In particular, if ![]() $Y^q_t$ contains at least one smooth point of
$Y^q_t$ contains at least one smooth point of ![]() $X^q_t(\mathbb{Q}_\ell)$, then it contains an open set of smooth points. The local dimension at each smooth point of
$X^q_t(\mathbb{Q}_\ell)$, then it contains an open set of smooth points. The local dimension at each smooth point of ![]() $X^q_t(\mathbb{Q}_\ell)$ is d. By construction of the measure µd (see again [Reference Oesterlé44, § 3]), an open subset of
$X^q_t(\mathbb{Q}_\ell)$ is d. By construction of the measure µd (see again [Reference Oesterlé44, § 3]), an open subset of ![]() $X^q_t(\mathbb{Q}_\ell)$ consisting of smooth points has positive measure: indeed, in the case of constant dimension d that we are considering here, µd is constructed locally by taking an analytic isometry between a ball in
$X^q_t(\mathbb{Q}_\ell)$ consisting of smooth points has positive measure: indeed, in the case of constant dimension d that we are considering here, µd is constructed locally by taking an analytic isometry between a ball in ![]() $(X^q_t)_{\operatorname{smooth}}$ and an open ball in
$(X^q_t)_{\operatorname{smooth}}$ and an open ball in ![]() $\mathbb{Q}_\ell^{d}$, and pulling back the Haar measure ν of
$\mathbb{Q}_\ell^{d}$, and pulling back the Haar measure ν of ![]() $\mathbb{Q}_\ell^{d}$, normalized by
$\mathbb{Q}_\ell^{d}$, normalized by ![]() $\nu(\mathbb{Z}_\ell^{d})=1$. It is then clear that any open set in
$\nu(\mathbb{Z}_\ell^{d})=1$. It is then clear that any open set in ![]() $(X^q_t)_{\operatorname{smooth}}$ has positive measure with respect to µd, and we have shown that
$(X^q_t)_{\operatorname{smooth}}$ has positive measure with respect to µd, and we have shown that ![]() $Y^q_t$ contains an open set of smooth points of
$Y^q_t$ contains an open set of smooth points of ![]() $X^q_t(\mathbb{Q}_\ell)$ as soon as it contains one. We are thus reduced to checking that
$X^q_t(\mathbb{Q}_\ell)$ as soon as it contains one. We are thus reduced to checking that ![]() $Y^q, Y_t^q$ contain at least one smooth point of
$Y^q, Y_t^q$ contain at least one smooth point of ![]() $X^q(\mathbb{Q}_\ell), X_t^q(\mathbb{Q}_\ell)$ respectively.
$X^q(\mathbb{Q}_\ell), X_t^q(\mathbb{Q}_\ell)$ respectively.
For Xq, which is smooth, this amounts to constructing a symplectic matrix with coefficients in ![]() $\mathbb{Z}_\ell$ and given multiplier; this follows immediately from either proposition 6.3 and remark 6.5 or from remark 4.2 after observing that the identity matrix lies in
$\mathbb{Z}_\ell$ and given multiplier; this follows immediately from either proposition 6.3 and remark 6.5 or from remark 4.2 after observing that the identity matrix lies in ![]() $\operatorname{Sp}_{2g}(\mathbb{Z}_\ell)$. For
$\operatorname{Sp}_{2g}(\mathbb{Z}_\ell)$. For ![]() $X^q_t$, we construct the relevant point explicitly.
$X^q_t$, we construct the relevant point explicitly.
We observe that ![]() $X^q_t$ arises as a fibre of the trace map:
$X^q_t$ arises as a fibre of the trace map:
i.e., ![]() $X^q_t=\text{trace}^{-1}(t)$. A sufficient condition for a point
$X^q_t=\text{trace}^{-1}(t)$. A sufficient condition for a point ![]() $P \in X^q_t$ to be smooth is the existence of a curve
$P \in X^q_t$ to be smooth is the existence of a curve ![]() $C \subseteq X^q$ containing P such that the restriction of the trace map
$C \subseteq X^q$ containing P such that the restriction of the trace map
has non-vanishing differential at P. To see this, notice that the dimension of the tangent space at P in ![]() $X^q_t$ is the dimension of the tangent space at P in Xq minus the dimension of the image of the differential of the trace map (restricted to Xq) at P. Let us fix the symplectic form
$X^q_t$ is the dimension of the tangent space at P in Xq minus the dimension of the image of the differential of the trace map (restricted to Xq) at P. Let us fix the symplectic form
 \begin{equation*}
\Omega= \begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\Omega= \begin{pmatrix}
0 & \operatorname{Id}_g \\
-\operatorname{Id}_g & 0
\end{pmatrix}.
\end{equation*} We consider the curve Ma, parametrized by ![]() $a \in \mathbb{A}^1$, given by
$a \in \mathbb{A}^1$, given by
 \begin{equation*}
M_a=
\begin{bmatrix}
a & z & a-q & z \\
{}^t z & q\operatorname{Id}_{g-1} & {}^t z & 0_{g-1} \\
1 & z & 1 & z \\
{}^t z & 0_{g-1} & {}^t z & \operatorname{Id}_{g-1}
\end{bmatrix}
\end{equation*}
\begin{equation*}
M_a=
\begin{bmatrix}
a & z & a-q & z \\
{}^t z & q\operatorname{Id}_{g-1} & {}^t z & 0_{g-1} \\
1 & z & 1 & z \\
{}^t z & 0_{g-1} & {}^t z & \operatorname{Id}_{g-1}
\end{bmatrix}
\end{equation*} where z is the ![]() $1 \times (g-1)$ vector
$1 \times (g-1)$ vector ![]() $(0,\ldots,0)$. One checks that
$(0,\ldots,0)$. One checks that ![]() $M_a \in X^q(\mathbb{Q}_\ell)$: up to a suitable change of basis, the symplectic form is represented by
$M_a \in X^q(\mathbb{Q}_\ell)$: up to a suitable change of basis, the symplectic form is represented by  $\operatorname{diag}\left( \begin{pmatrix}
0 & 1 \\ -1 & 0
\end{pmatrix}, \ldots, \begin{pmatrix}
0 & 1 \\ -1 & 0
\end{pmatrix} \right)$, and in the same basis Ma becomes the matrix
$\operatorname{diag}\left( \begin{pmatrix}
0 & 1 \\ -1 & 0
\end{pmatrix}, \ldots, \begin{pmatrix}
0 & 1 \\ -1 & 0
\end{pmatrix} \right)$, and in the same basis Ma becomes the matrix  $\operatorname{diag}\left( \begin{pmatrix}
a & a-q \\ 1 & 1
\end{pmatrix}, \begin{pmatrix}
1 & 0 \\ 0 & q
\end{pmatrix}, \ldots, \begin{pmatrix}
1 & 0 \\ 0 & q
\end{pmatrix} \right)$, which is manifestly symplectic since every
$\operatorname{diag}\left( \begin{pmatrix}
a & a-q \\ 1 & 1
\end{pmatrix}, \begin{pmatrix}
1 & 0 \\ 0 & q
\end{pmatrix}, \ldots, \begin{pmatrix}
1 & 0 \\ 0 & q
\end{pmatrix} \right)$, which is manifestly symplectic since every ![]() $2 \times 2$ block has determinant q. Moreover,
$2 \times 2$ block has determinant q. Moreover, ![]() $\text{trace}(M_a)=a+qg-q+g$; the composition
$\text{trace}(M_a)=a+qg-q+g$; the composition
is just a translation of ![]() $\mathbb{A}^1$, which implies that the differential of the trace map at Ma is surjective. Therefore, the point
$\mathbb{A}^1$, which implies that the differential of the trace map at Ma is surjective. Therefore, the point ![]() $M_{t-qg+q-g} \in X^{q}_t$ is smooth and its entries are elements of
$M_{t-qg+q-g} \in X^{q}_t$ is smooth and its entries are elements of ![]() $\mathbb{Z}_{\ell}$. This concludes the proof.
$\mathbb{Z}_{\ell}$. This concludes the proof.
5. Proof of theorem 1.4
The goal of this section is to show that the set ![]() $\mathcal{P}_g(\mathbb{F}_q)$ of definition 1.2 spans a
$\mathcal{P}_g(\mathbb{F}_q)$ of definition 1.2 spans a ![]() $\mathbb{Q}$-vector space of dimension g + 1 for all pairs (g, q). For a fixed genus g and
$\mathbb{Q}$-vector space of dimension g + 1 for all pairs (g, q). For a fixed genus g and ![]() $q \gg_g 1$, this follows from theorem 2.1 (see remark 2.9). Studying more precisely the set
$q \gg_g 1$, this follows from theorem 2.1 (see remark 2.9). Studying more precisely the set ![]() $\mathcal{P}_{g, 2}(\mathbb{F}_q)$ for every fixed value of q, we prove the statement for all q and g. Recall that
$\mathcal{P}_{g, 2}(\mathbb{F}_q)$ for every fixed value of q, we prove the statement for all q and g. Recall that ![]() $\mathcal{P}_g(\mathbb{F}_q)$ is defined in definition 1.2 and
$\mathcal{P}_g(\mathbb{F}_q)$ is defined in definition 1.2 and ![]() $\mathcal{P}_{g, 2}(\mathbb{F}_q)$ is its reduction modulo 2. As we pointed out in the introduction, we split our proof of theorem 1.4 into two parts, one for the case p odd and one for the case p = 2, since the properties of the 2-torsion points are slightly different when the characteristic is odd or even.
$\mathcal{P}_{g, 2}(\mathbb{F}_q)$ is its reduction modulo 2. As we pointed out in the introduction, we split our proof of theorem 1.4 into two parts, one for the case p odd and one for the case p = 2, since the properties of the 2-torsion points are slightly different when the characteristic is odd or even.
5.1. Proof of theorem 1.4: p odd
Throughout this section, the prime ![]() $p=\operatorname{char}(\mathbb{F}_q)$ is assumed to be odd. Thanks to theorem 1.7, it makes sense to define
$p=\operatorname{char}(\mathbb{F}_q)$ is assumed to be odd. Thanks to theorem 1.7, it makes sense to define ![]() $f_{C}(t) \in \mathbb{Z}[t]$ as
$f_{C}(t) \in \mathbb{Z}[t]$ as ![]() $f_{C, \ell^\infty}(t)$, where
$f_{C, \ell^\infty}(t)$, where ![]() $\ell$ is any prime different from p; from now on, we shall choose
$\ell$ is any prime different from p; from now on, we shall choose ![]() $\ell=2$. This choice has the additional advantage that working modulo 2 makes the connection between the L-polynomial and the characteristic polynomial of Frobenius particularly simple:
$\ell=2$. This choice has the additional advantage that working modulo 2 makes the connection between the L-polynomial and the characteristic polynomial of Frobenius particularly simple:
Corollary 5.1. We have ![]() $P_{C}(t) \equiv f_{C}(t)\ (\mathrm{mod}\ 2)$.
$P_{C}(t) \equiv f_{C}(t)\ (\mathrm{mod}\ 2)$.
Proof. Write  $P_{C}(t)=\sum_{i=0}^{2g} a_i t^i \in \mathbb{Z}[t]$ and
$P_{C}(t)=\sum_{i=0}^{2g} a_i t^i \in \mathbb{Z}[t]$ and  $f_{C}(t)=\sum_{i=0}^{2g} b_i t^i$. By theorem 1.7, we have the equality
$f_{C}(t)=\sum_{i=0}^{2g} b_i t^i$. By theorem 1.7, we have the equality ![]() $b_i=a_{2g-i}$, and since q is odd we also have
$b_i=a_{2g-i}$, and since q is odd we also have ![]() $
b_i=a_{2g-i}=q^{g-i}a_i \equiv a_i\ (\mathrm{mod}\ 2)
$.
$
b_i=a_{2g-i}=q^{g-i}a_i \equiv a_i\ (\mathrm{mod}\ 2)
$.
We now recall a concrete description for the vector space of 2-torsion points of a hyperelliptic Jacobian, at least in the case when the hyperelliptic model is given by a polynomial of odd degree. Let ![]() $f(x) \in \mathbb{F}_q[x]$ be a separable polynomial of degree
$f(x) \in \mathbb{F}_q[x]$ be a separable polynomial of degree ![]() $2g+1$ and let
$2g+1$ and let ![]() $C/\mathbb{F}_q$ be the unique smooth projective curve birational to the affine curve
$C/\mathbb{F}_q$ be the unique smooth projective curve birational to the affine curve ![]() $
y^2=f(x).
$ Furthermore, let
$
y^2=f(x).
$ Furthermore, let ![]() $J/\mathbb{F}_q$ be the Jacobian of C and
$J/\mathbb{F}_q$ be the Jacobian of C and ![]() $\{\alpha_1,\ldots,\alpha_{2g+1}\}$ be the set of roots of f(x) in
$\{\alpha_1,\ldots,\alpha_{2g+1}\}$ be the set of roots of f(x) in ![]() $\overline{\mathbb{F}_q}$. Then for
$\overline{\mathbb{F}_q}$. Then for ![]() $i=1,\ldots,2g+1$, we have a point
$i=1,\ldots,2g+1$, we have a point ![]() $(\alpha_i,0) \in C(\overline{\mathbb{F}_q})$; also notice that C, being given by an odd-degree model, has a unique point at infinity, which we denote by
$(\alpha_i,0) \in C(\overline{\mathbb{F}_q})$; also notice that C, being given by an odd-degree model, has a unique point at infinity, which we denote by ![]() $\infty$. We denote by
$\infty$. We denote by ![]() $R_i = [(\alpha_i,0)-\infty]$ the classes of the divisors
$R_i = [(\alpha_i,0)-\infty]$ the classes of the divisors ![]() $Q_i=(\alpha_i,0)-\infty$ in
$Q_i=(\alpha_i,0)-\infty$ in ![]() $J(\overline{\mathbb{F}_q})$. We then have the following well-known description for the 2-torsion of J (see for example [Reference Gross25, Section 4]):
$J(\overline{\mathbb{F}_q})$. We then have the following well-known description for the 2-torsion of J (see for example [Reference Gross25, Section 4]):
Lemma 5.2. The following hold:
1. Each of the divisor classes
 $R_i \in J(\overline{\mathbb{F}_q})$ represents a point of order 2.
$R_i \in J(\overline{\mathbb{F}_q})$ represents a point of order 2.2. The classes Ri span
 $J[2]$.
$J[2]$.3. The only linear relation satisfied by the Ri is
 $R_1+\cdots+R_{2g+1}=0$.
$R_1+\cdots+R_{2g+1}=0$.
We can now compute the action of Frobenius on the 2-torsion points of C. A similar result appeared independently in [Reference Costa, Donepudi, Fernando, Karemaker, Springer and West16, proposition 2.4].
Lemma 5.3. With notation as above, write ![]() $f(x)=\prod_{i=1}^r f_i(x)$ for the factorization of f(x) as a product of irreducible polynomials in
$f(x)=\prod_{i=1}^r f_i(x)$ for the factorization of f(x) as a product of irreducible polynomials in ![]() $\mathbb{F}_q[x]$, and let
$\mathbb{F}_q[x]$, and let ![]() $d_i=\deg(f_i)$. Let
$d_i=\deg(f_i)$. Let  $\rho_2 : \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{Aut}_{\mathbb{F}_2}(J[2])$ be the Galois representation attached to the 2-torsion points of J. Then
$\rho_2 : \operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{Aut}_{\mathbb{F}_2}(J[2])$ be the Galois representation attached to the 2-torsion points of J. Then
 \begin{equation*}
f_{C,2}(t) =\det( t\operatorname{Id}- \rho_2(\operatorname{Frob}))=(t-1)^{-1} \prod_{i=1}^r (t^{d_i}-1) \in \mathbb{F}_2[t].
\end{equation*}
\begin{equation*}
f_{C,2}(t) =\det( t\operatorname{Id}- \rho_2(\operatorname{Frob}))=(t-1)^{-1} \prod_{i=1}^r (t^{d_i}-1) \in \mathbb{F}_2[t].
\end{equation*}Proof. As above, let ![]() $\infty$ be the unique point at infinity of C, and for
$\infty$ be the unique point at infinity of C, and for ![]() $i=1,\ldots,2g+1$ let
$i=1,\ldots,2g+1$ let ![]() $Q_i=(\alpha_i,0)-\infty \in \operatorname{Div}_{C}(\overline{\mathbb{F}_q})$. Write Pi for the image of Qi in the
$Q_i=(\alpha_i,0)-\infty \in \operatorname{Div}_{C}(\overline{\mathbb{F}_q})$. Write Pi for the image of Qi in the ![]() $\mathbb{F}_2$-vector space
$\mathbb{F}_2$-vector space ![]() $\operatorname{Div}_{C}(\overline{\mathbb{F}_q})\otimes \mathbb{F}_2$, and let V be the
$\operatorname{Div}_{C}(\overline{\mathbb{F}_q})\otimes \mathbb{F}_2$, and let V be the ![]() $(2g+1)$-dimensional
$(2g+1)$-dimensional ![]() $\mathbb{F}_2$-vector subspace of
$\mathbb{F}_2$-vector subspace of ![]() $\operatorname{Div}_{C}(\overline{\mathbb{F}_q})\otimes \mathbb{F}_2$ spanned by the Pi. There is a natural action of
$\operatorname{Div}_{C}(\overline{\mathbb{F}_q})\otimes \mathbb{F}_2$ spanned by the Pi. There is a natural action of ![]() $\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on V, which we consider as a representation
$\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q)$ on V, which we consider as a representation ![]() $\rho:\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}(V)$. By Galois theory, it is clear that
$\rho:\operatorname{Gal}(\overline{\mathbb{F}_q}/\mathbb{F}_q) \to \operatorname{GL}(V)$. By Galois theory, it is clear that ![]() $\operatorname{Frob}$ acts on the set
$\operatorname{Frob}$ acts on the set  $\{\alpha_i\}_{i=1}^{2g+1}$ with r orbits, one corresponding to each irreducible factor of f(x). The lengths of the orbits are given by the degrees di of the factors
$\{\alpha_i\}_{i=1}^{2g+1}$ with r orbits, one corresponding to each irreducible factor of f(x). The lengths of the orbits are given by the degrees di of the factors ![]() $f_i(x)$. This means that, in the natural basis of V given by the Pi, the action of Frobenius is given by a permutation matrix corresponding to a permutation of cycle type
$f_i(x)$. This means that, in the natural basis of V given by the Pi, the action of Frobenius is given by a permutation matrix corresponding to a permutation of cycle type ![]() $
(d_1, d_2, \ldots, d_r)
$. It follows immediately that the characteristic polynomial of
$
(d_1, d_2, \ldots, d_r)
$. It follows immediately that the characteristic polynomial of ![]() $\rho(\operatorname{Frob})$ is
$\rho(\operatorname{Frob})$ is
On the other hand, by lemma 5.2, there is a Galois-equivariant exact sequence
where the first map is given by ![]() $1\to P_1+P_2+\cdots P_{2g+1}$ and the action of
$1\to P_1+P_2+\cdots P_{2g+1}$ and the action of ![]() $\operatorname{Frob}$ on the sum
$\operatorname{Frob}$ on the sum ![]() $P_1+\cdots+P_{2g+1}$ is trivial. This implies that
$P_1+\cdots+P_{2g+1}$ is trivial. This implies that
which, combined with our previous determination of the characteristic polynomial of ![]() $\rho(\operatorname{Frob})$, concludes the proof.
$\rho(\operatorname{Frob})$, concludes the proof.
Thanks to the previous lemma, it is easy to obtain the reduction modulo 2 of the L-polynomial of any given hyperelliptic curve with an odd degree model. In the next corollary, we use this to produce curves whose L-polynomials have particularly simple reductions modulo 2.
Corollary 5.4. Let ![]() $f_0(x)=1$ and, for
$f_0(x)=1$ and, for ![]() $d=1,\ldots,2g+1$, let
$d=1,\ldots,2g+1$, let ![]() $f_d(x) \in \mathbb{F}_q[x]$ be an irreducible polynomial of degree d. Further set
$f_d(x) \in \mathbb{F}_q[x]$ be an irreducible polynomial of degree d. Further set ![]() $f_0(x)=1$. For
$f_0(x)=1$. For ![]() $d=0,\ldots,g$ consider the unique smooth projective curve Cd birational to the affine curve
$d=0,\ldots,g$ consider the unique smooth projective curve Cd birational to the affine curve
 \begin{equation*}
y^2=f_d(x)f_{2g+1-d}(x).
\end{equation*}
\begin{equation*}
y^2=f_d(x)f_{2g+1-d}(x).
\end{equation*} For ![]() $d=1,\ldots,g$, we have the congruence
$d=1,\ldots,g$, we have the congruence
 \begin{equation*}
(t-1)P_{C_d}(t) \equiv (t^d-1)(t^{2g+1-d}-1) \equiv t^{2g+1}+t^{2g+1-d} +t^d +1\ (\mathrm{mod}\ 2),
\end{equation*}
\begin{equation*}
(t-1)P_{C_d}(t) \equiv (t^d-1)(t^{2g+1-d}-1) \equiv t^{2g+1}+t^{2g+1-d} +t^d +1\ (\mathrm{mod}\ 2),
\end{equation*}while for d = 0 we have
 \begin{equation*}
(t-1)P_{C_0}(t) \equiv t^{2g+1}-1 \equiv t^{2g+1} +1\ (\mathrm{mod}\ 2).
\end{equation*}
\begin{equation*}
(t-1)P_{C_0}(t) \equiv t^{2g+1}-1 \equiv t^{2g+1} +1\ (\mathrm{mod}\ 2).
\end{equation*}Proof. This is a direct application of lemma 5.3, combined with the fact that by corollary 5.1 we have ![]() $P_{C}(t) \equiv f_{C}(t)\ (\mathrm{mod}\ 2)$.
$P_{C}(t) \equiv f_{C}(t)\ (\mathrm{mod}\ 2)$.
Proof of theorem 1.4 for p odd
The inequality ![]() $\dim_{\mathbb{Q}} L_g(\mathbb{F}_q) \leq g+1$ follows immediately from the symmetry relation
$\dim_{\mathbb{Q}} L_g(\mathbb{F}_q) \leq g+1$ follows immediately from the symmetry relation ![]() $a_{g+i}=q^ia_{g-i}$ satisfied by the coefficients of the L-polynomials; it thus suffices to establish the lower bound
$a_{g+i}=q^ia_{g-i}$ satisfied by the coefficients of the L-polynomials; it thus suffices to establish the lower bound ![]() $\dim_{\mathbb{Q}} L_g(\mathbb{F}_q) \geq g+1$. Consider the g + 1 curves
$\dim_{\mathbb{Q}} L_g(\mathbb{F}_q) \geq g+1$. Consider the g + 1 curves ![]() $C_0,\ldots,C_g$ of corollary 5.4 (any choice of the irreducible polynomials
$C_0,\ldots,C_g$ of corollary 5.4 (any choice of the irreducible polynomials ![]() $f_d(x)$ will work) and the corresponding L-polynomials
$f_d(x)$ will work) and the corresponding L-polynomials ![]() $P_{C_0}(t),\ldots,P_{C_g}(t)$. Let
$P_{C_0}(t),\ldots,P_{C_g}(t)$. Let ![]() $M \subseteq \mathbb{Z}[t]$ be the
$M \subseteq \mathbb{Z}[t]$ be the ![]() $\mathbb{Z}$-module generated by these polynomials; it is clear that in order to prove the theorem it suffices to show that
$\mathbb{Z}$-module generated by these polynomials; it is clear that in order to prove the theorem it suffices to show that ![]() $\operatorname{rank}_{\mathbb{Z}} M \geq g+1$. Notice that
$\operatorname{rank}_{\mathbb{Z}} M \geq g+1$. Notice that ![]() $M \otimes \mathbb{F}_2$ is in a natural way a vector subspace of
$M \otimes \mathbb{F}_2$ is in a natural way a vector subspace of ![]() $\mathbb{F}_2[t]$, and that
$\mathbb{F}_2[t]$, and that
Let ![]() $N \subset \mathbb{F}_2[t]$ be the image of the linear map
$N \subset \mathbb{F}_2[t]$ be the image of the linear map
 \begin{equation*}
\begin{array}{ccc}
M \otimes \mathbb{F}_2 & \to & \mathbb{F}_2[t] \\
q(t) & \mapsto & (t-1)q(t).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
M \otimes \mathbb{F}_2 & \to & \mathbb{F}_2[t] \\
q(t) & \mapsto & (t-1)q(t).
\end{array}
\end{equation*} The ![]() $\mathbb{F}_2$-vector space N is generated by the g + 1 polynomials
$\mathbb{F}_2$-vector space N is generated by the g + 1 polynomials ![]() $(t-1)P_{C_i}(t)$ for
$(t-1)P_{C_i}(t)$ for ![]() $i=0,\ldots,g$, hence, by corollary 5.4, by the g + 1 polynomials
$i=0,\ldots,g$, hence, by corollary 5.4, by the g + 1 polynomials
It is immediate to check that these g + 1 polynomials are ![]() $\mathbb{F}_2$-linearly independent, which implies
$\mathbb{F}_2$-linearly independent, which implies
5.2. Proof of theorem 1.4: p = 2
We now give the proof of theorem 1.4 in the case p = 2. As in the case of odd characteristic, we will exhibit g + 1 curves whose L-polynomials form a basis of ![]() $L_g(\mathbb{F}_q)$. Recall from definition 1.2 the set
$L_g(\mathbb{F}_q)$. Recall from definition 1.2 the set ![]() $\mathcal{P}_g(\mathbb{F}_q)$.
$\mathcal{P}_g(\mathbb{F}_q)$.
Proof of theorem 1.4 for p = 2
Fix ![]() $0\leq r\leq g$. Let
$0\leq r\leq g$. Let ![]() $h(x) \in \mathbb{F}_q[x]$ be a separable polynomial of degree r such that
$h(x) \in \mathbb{F}_q[x]$ be a separable polynomial of degree r such that ![]() $h(0)\neq 0$. Such a polynomial exists: for
$h(0)\neq 0$. Such a polynomial exists: for ![]() $r=0, 1$ we may take
$r=0, 1$ we may take ![]() $h(x)=1$ or
$h(x)=1$ or ![]() $h(x)=x+1$, respectively, and for
$h(x)=x+1$, respectively, and for ![]() $r \geq 2$ it suffices to take as h(x) the minimal polynomial of any element that generates
$r \geq 2$ it suffices to take as h(x) the minimal polynomial of any element that generates ![]() $\mathbb{F}_{q^r}$ over
$\mathbb{F}_{q^r}$ over ![]() $\mathbb{F}_q$.
$\mathbb{F}_q$.
Consider the affine curve defined by the equation ![]() $y^2+yh(x)=x^{2g+1-r}h(x)$. We claim that this curve is smooth. Indeed, an
$y^2+yh(x)=x^{2g+1-r}h(x)$. We claim that this curve is smooth. Indeed, an ![]() $\overline{\mathbb{F}_q}$-point
$\overline{\mathbb{F}_q}$-point ![]() $(x_0,y_0)$ on the curve is singular if and only if
$(x_0,y_0)$ on the curve is singular if and only if
 \begin{equation*}
\begin{cases}
y_0^2+y_0h(x_0)=x_0^{2g+1-r}h(x_0)\\
h(x_0)=0\\
y_0h'(x_0)=(2g+1-r)x_0^{2g-r}h(x_0)+x_0^{2g+1-r}h'(x_0)
\end{cases}.
\end{equation*}
\begin{equation*}
\begin{cases}
y_0^2+y_0h(x_0)=x_0^{2g+1-r}h(x_0)\\
h(x_0)=0\\
y_0h'(x_0)=(2g+1-r)x_0^{2g-r}h(x_0)+x_0^{2g+1-r}h'(x_0)
\end{cases}.
\end{equation*} Here the second and third equations are given by the vanishing of the partial derivatives in y and x of the defining equation, respectively. By the second equation, x 0 is a root of h. So, by the first one, ![]() $y_0=0$. Hence, the third equation becomes
$y_0=0$. Hence, the third equation becomes  $x_0^{2g+1-r}h'(x_0)=0$: but
$x_0^{2g+1-r}h'(x_0)=0$: but ![]() $x_0\neq 0$ since
$x_0\neq 0$ since ![]() $h(0)\neq 0$, and
$h(0)\neq 0$, and ![]() $h'(x_0)\neq 0$ since h is separable, so the above system has no solutions. Let
$h'(x_0)\neq 0$ since h is separable, so the above system has no solutions. Let ![]() $C/\mathbb{F}_q$ be the smooth projective curve given by the completion of the curve above. The curve C has genus g, because the degree of
$C/\mathbb{F}_q$ be the smooth projective curve given by the completion of the curve above. The curve C has genus g, because the degree of ![]() $x^{2g+1-r}h(x)$ is
$x^{2g+1-r}h(x)$ is ![]() $2g+1$ and the degree of h(x) is at most g. In particular,
$2g+1$ and the degree of h(x) is at most g. In particular, ![]() $P_C(t)$ is an element of
$P_C(t)$ is an element of ![]() $\mathcal{P}_g(\mathbb{F}_q)$. We will show that the reduction of
$\mathcal{P}_g(\mathbb{F}_q)$. We will show that the reduction of ![]() $P_C(t)$ modulo 2 has degree r.
$P_C(t)$ modulo 2 has degree r.
Let ![]() $\ell$ be an odd prime and let
$\ell$ be an odd prime and let ![]() $T_\ell J$ be the
$T_\ell J$ be the ![]() $\ell$-adic Tate module of the Jacobian J of C. Let
$\ell$-adic Tate module of the Jacobian J of C. Let ![]() $f_{C, \ell^\infty}(t):=\det(t\operatorname{Id}-\rho_{\ell^\infty}(\operatorname{Frob})\mid T_\ell J)$. If
$f_{C, \ell^\infty}(t):=\det(t\operatorname{Id}-\rho_{\ell^\infty}(\operatorname{Frob})\mid T_\ell J)$. If ![]() $\alpha\in \overline{\mathbb{F}_q}$ is a root of
$\alpha\in \overline{\mathbb{F}_q}$ is a root of ![]() $f_{C, \ell^\infty}(t)$ with multiplicity d, then
$f_{C, \ell^\infty}(t)$ with multiplicity d, then ![]() $q/\alpha$ is a root of
$q/\alpha$ is a root of ![]() $f_{C, \ell^\infty}(t)$ with multiplicity d. Hence, we can write
$f_{C, \ell^\infty}(t)$ with multiplicity d. Hence, we can write ![]() $f_{C, \ell^\infty}(t)=t^gQ_C(t+q/t)$ with
$f_{C, \ell^\infty}(t)=t^gQ_C(t+q/t)$ with ![]() $Q_C(t)\in \mathbb{Z}[t]$ of degree g. Let r 2 be the 2-rank of J, as defined in [Reference González24, Section 1]. By [Reference González24, proposition 3.1], r 2 is equal to the sum of the multiplicities of the non-zero roots of
$Q_C(t)\in \mathbb{Z}[t]$ of degree g. Let r 2 be the 2-rank of J, as defined in [Reference González24, Section 1]. By [Reference González24, proposition 3.1], r 2 is equal to the sum of the multiplicities of the non-zero roots of ![]() $Q_C(t)$ modulo 2. Hence,
$Q_C(t)$ modulo 2. Hence,
with ![]() $\tilde{Q}_C(t)\in \mathbb{F}_2[t]$ a polynomial of degree r 2 such that
$\tilde{Q}_C(t)\in \mathbb{F}_2[t]$ a polynomial of degree r 2 such that ![]() $\tilde{Q}_C(0)\neq 0$ (in
$\tilde{Q}_C(0)\neq 0$ (in ![]() $\mathbb{F}_2$). In [Reference Castryck, Streng and Testa14, proof of theorem 23], the authors show that the 2-rank of J is equal to one less than the number of distinct projective points where
$\mathbb{F}_2$). In [Reference Castryck, Streng and Testa14, proof of theorem 23], the authors show that the 2-rank of J is equal to one less than the number of distinct projective points where ![]() $H_1(X, Z) := h(X/Z)Z^{g+1}$ vanishes (see also [Reference Elkin and Pries21]). In our case, since h(x) is separable, this implies
$H_1(X, Z) := h(X/Z)Z^{g+1}$ vanishes (see also [Reference Elkin and Pries21]). In our case, since h(x) is separable, this implies ![]() $r_2 = \deg h(x) = r$. Hence, we have
$r_2 = \deg h(x) = r$. Hence, we have
with ![]() $\tilde{Q}_C(t)$ of degree r. As q is a power of 2, we obtain
$\tilde{Q}_C(t)$ of degree r. As q is a power of 2, we obtain
 \begin{equation*}
f_{C, \ell^\infty}(t)\equiv t^gQ_C\left(t+\frac qt\right)\equiv t^gQ_C\left(t\right)\equiv t^{2g-r}\tilde{Q}_C(t)(\mathrm{mod}\ 2).
\end{equation*}
\begin{equation*}
f_{C, \ell^\infty}(t)\equiv t^gQ_C\left(t+\frac qt\right)\equiv t^gQ_C\left(t\right)\equiv t^{2g-r}\tilde{Q}_C(t)(\mathrm{mod}\ 2).
\end{equation*}By theorem 1.7,
 \begin{equation}
P_C(t)\equiv t^{2g}f_{C, \ell^\infty}\left(t^{-1}\right)\equiv t^{2g}t^{-2g+r}\tilde{Q}_C\left(t^{-1}\right)\equiv t^r \tilde{Q}_C\left(t^{-1}\right)(\mathrm{mod}\ 2).
\end{equation}
\begin{equation}
P_C(t)\equiv t^{2g}f_{C, \ell^\infty}\left(t^{-1}\right)\equiv t^{2g}t^{-2g+r}\tilde{Q}_C\left(t^{-1}\right)\equiv t^r \tilde{Q}_C\left(t^{-1}\right)(\mathrm{mod}\ 2).
\end{equation} Since ![]() $\tilde{Q}_C(0)\not\equiv 0(\mathrm{mod}\ 2)$, we see that the reduction of
$\tilde{Q}_C(0)\not\equiv 0(\mathrm{mod}\ 2)$, we see that the reduction of ![]() $P_C(t)$ modulo 2 has degree r. So, for each
$P_C(t)$ modulo 2 has degree r. So, for each ![]() $0\leq r\leq g$, we can find a smooth hyperelliptic curve Cr of genus g such that
$0\leq r\leq g$, we can find a smooth hyperelliptic curve Cr of genus g such that ![]() $P_{C_r}(t)$ modulo 2 has degree r. Therefore, the polynomials
$P_{C_r}(t)$ modulo 2 has degree r. Therefore, the polynomials ![]() $\{P_{C_r}(t)\mid 0\leq r\leq g\}$ are linearly independent modulo 2. The result follows as in the proof of theorem 1.4.
$\{P_{C_r}(t)\mid 0\leq r\leq g\}$ are linearly independent modulo 2. The result follows as in the proof of theorem 1.4.
Remark 5.5. The polynomial ![]() $f_{C, \ell^\infty}(t)$ is monic by definition, which implies that also
$f_{C, \ell^\infty}(t)$ is monic by definition, which implies that also ![]() $Q_C(t)$ and
$Q_C(t)$ and ![]() $\tilde{Q}_C(t)$ are monic. By (24), the constant term of
$\tilde{Q}_C(t)$ are monic. By (24), the constant term of ![]() $P_C(t)$ modulo 2 is 1. Hence,
$P_C(t)$ modulo 2 is 1. Hence,
 \begin{equation*}
P_{C_r}(t)\equiv t^r+1+\sum_{i=1}^{r-1} a_{i,r}t^i(\mathrm{mod}\ 2).
\end{equation*}
\begin{equation*}
P_{C_r}(t)\equiv t^r+1+\sum_{i=1}^{r-1} a_{i,r}t^i(\mathrm{mod}\ 2).
\end{equation*} In fact, one can show that ![]() $P_{C_r}(t) \equiv t^r+1(\mathrm{mod}\ 2)$. To see this, recall from [Reference Deligne and Katz18, theorem 3.1] that, for a smooth projective curve
$P_{C_r}(t) \equiv t^r+1(\mathrm{mod}\ 2)$. To see this, recall from [Reference Deligne and Katz18, theorem 3.1] that, for a smooth projective curve ![]() $C / \mathbb{F}_q$, with
$C / \mathbb{F}_q$, with ![]() $q=2^f$, one has
$q=2^f$, one has
 \begin{equation*}
P_{C}(t) \equiv \det\left(1-t \varphi_q^{-1} \bigm\vert H^1_{\text{\'{e}t}}\left( C_{\overline{\mathbb{F}_q}}, \mathbb{Z}/2\mathbb{Z} \right) \right)\ (\mathrm{mod}\ 2),
\end{equation*}
\begin{equation*}
P_{C}(t) \equiv \det\left(1-t \varphi_q^{-1} \bigm\vert H^1_{\text{\'{e}t}}\left( C_{\overline{\mathbb{F}_q}}, \mathbb{Z}/2\mathbb{Z} \right) \right)\ (\mathrm{mod}\ 2),
\end{equation*} where ![]() $\varphi_q : \mathbb{F}_q \to \mathbb{F}_q$ is the Frobenius automorphism
$\varphi_q : \mathbb{F}_q \to \mathbb{F}_q$ is the Frobenius automorphism ![]() $x \mapsto x^q$. Next, recall that
$x \mapsto x^q$. Next, recall that  $H^1_{\text{\'{e}t}}\left( C_{\overline{\mathbb{F}_q}}, \mathbb{Z}/2\mathbb{Z} \right)$ is canonically dual to
$H^1_{\text{\'{e}t}}\left( C_{\overline{\mathbb{F}_q}}, \mathbb{Z}/2\mathbb{Z} \right)$ is canonically dual to ![]() $J(\overline{\mathbb{F}_q})[2]$, so that we may compute
$J(\overline{\mathbb{F}_q})[2]$, so that we may compute ![]() $P_{C}(t)$ as the inverse characteristic polynomial of Frobenius acting on
$P_{C}(t)$ as the inverse characteristic polynomial of Frobenius acting on ![]() $J[2]$. For the curve Cr, the explicit description of
$J[2]$. For the curve Cr, the explicit description of ![]() $J[2]$ given in [Reference Castryck, Streng and Testa14, proof of theorem 23] shows that the action of φq on
$J[2]$ given in [Reference Castryck, Streng and Testa14, proof of theorem 23] shows that the action of φq on ![]() $J[2]$ is the natural Galois action on the roots of h(x), that is, an r-cycle. It follows that the characteristic polynomial in question is
$J[2]$ is the natural Galois action on the roots of h(x), that is, an r-cycle. It follows that the characteristic polynomial in question is ![]() $P_{C}(t) \equiv t^r-1\ (\mathrm{mod}\ 2)$, as claimed.
$P_{C}(t) \equiv t^r-1\ (\mathrm{mod}\ 2)$, as claimed.
6. Algebraic independence
Theorem 1.4 asserts that lemma 1.1 captures all the linear relations among the coefficients of the polynomials ![]() $P_C(t)$. In this section, we prove an analogous result that deals with higher-order polynomial relations on the coefficients. Lemma 1.1 already gives a number of constraints: for
$P_C(t)$. In this section, we prove an analogous result that deals with higher-order polynomial relations on the coefficients. Lemma 1.1 already gives a number of constraints: for  $P_C(t)=\sum_{i=0}^{2g} a_i t^i$ we have
$P_C(t)=\sum_{i=0}^{2g} a_i t^i$ we have ![]() $a_0=1$ and
$a_0=1$ and ![]() $a_{g+i}=q^i a_{g-i}$ for every
$a_{g+i}=q^i a_{g-i}$ for every ![]() $i=0, \ldots, g$; it is, therefore, natural to restrict our analysis to
$i=0, \ldots, g$; it is, therefore, natural to restrict our analysis to ![]() $a_1,\ldots,a_g$. The following is the main result of this section:
$a_1,\ldots,a_g$. The following is the main result of this section:
Theorem 6.1. Let ![]() $g,d$ be positive integers. There is a constant
$g,d$ be positive integers. There is a constant ![]() $e_{g,d}$ such that for any prime power
$e_{g,d}$ such that for any prime power ![]() $q \gt e_{g,d}$ and for any non-zero polynomial
$q \gt e_{g,d}$ and for any non-zero polynomial ![]() $f(x_1,\ldots,x_g) \in \mathbb{Z}[x_1,\ldots,x_g]$ of degree
$f(x_1,\ldots,x_g) \in \mathbb{Z}[x_1,\ldots,x_g]$ of degree ![]() $\le d$ in each variable there is a curve
$\le d$ in each variable there is a curve ![]() $C \in \mathcal{M}_g(\mathbb{F}_q)$ with L-polynomial
$C \in \mathcal{M}_g(\mathbb{F}_q)$ with L-polynomial  $P_C(t)=\sum_{i=0}^{2g} a_i t^i$ such that
$P_C(t)=\sum_{i=0}^{2g} a_i t^i$ such that ![]() $f(a_1,\ldots,a_g) \neq 0$.
$f(a_1,\ldots,a_g) \neq 0$.
Notice that, unlike theorem 1.4, ![]() $e_{g,d}$ cannot be equal to 0 for all g and d, since for fixed q and g we can always find a polynomial
$e_{g,d}$ cannot be equal to 0 for all g and d, since for fixed q and g we can always find a polynomial ![]() $f(x_1,\ldots,x_g)$ (that may depend on q) which vanishes on all the finitely many values of
$f(x_1,\ldots,x_g)$ (that may depend on q) which vanishes on all the finitely many values of ![]() $(a_1,\ldots,a_g)$.
$(a_1,\ldots,a_g)$.
As is the case for theorem 1.4, the proof of theorem 6.1 exploits the reduction of ![]() $f(x_1,\ldots,x_g)$ modulo a positive integer N. In this case, instead of a direct computation of the action of the Frobenius on the N-torsion points, we use theorem 2.1, which guarantees that, for q large enough, all the characteristic polynomials of the matrices in
$f(x_1,\ldots,x_g)$ modulo a positive integer N. In this case, instead of a direct computation of the action of the Frobenius on the N-torsion points, we use theorem 2.1, which guarantees that, for q large enough, all the characteristic polynomials of the matrices in  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ come from some element of
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ come from some element of ![]() $\mathcal{P}_{g,N}(\mathbb{F}_q)$.
$\mathcal{P}_{g,N}(\mathbb{F}_q)$.
To be more precise, for a curve ![]() $C \in \mathcal{M}_g(\mathbb{F}_q)$ and
$C \in \mathcal{M}_g(\mathbb{F}_q)$ and ![]() $P_C(t) \in \mathbb{Z}[t]$ its L-polynomial, let
$P_C(t) \in \mathbb{Z}[t]$ its L-polynomial, let ![]() $f_C(t)=t^{2g}P_C(1/t)$ be its reciprocal polynomial. By theorem 1.7,
$f_C(t)=t^{2g}P_C(1/t)$ be its reciprocal polynomial. By theorem 1.7, ![]() $f_C(t)$ is equal to the characteristic polynomial of the action of the Frobenius of C (modulo every
$f_C(t)$ is equal to the characteristic polynomial of the action of the Frobenius of C (modulo every ![]() $\ell$). Theorem 2.1 implies that, for q large enough (in terms of N) and for any
$\ell$). Theorem 2.1 implies that, for q large enough (in terms of N) and for any  $M \in \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$, the characteristic polynomial of M is equal to the reduction of
$M \in \operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$, the characteristic polynomial of M is equal to the reduction of ![]() $f_C(t)$ modulo N for some
$f_C(t)$ modulo N for some ![]() $C \in \mathcal{M}_g(\mathbb{F}_q)$. We then prove that there are too many characteristic polynomials of elements of
$C \in \mathcal{M}_g(\mathbb{F}_q)$. We then prove that there are too many characteristic polynomials of elements of  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ for their coefficients to lie in the zero locus of some
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/N\mathbb{Z})$ for their coefficients to lie in the zero locus of some ![]() $f(x_1,\ldots,x_g)$ of fixed degree. We are free to choose N, and we will always take it to be an odd prime number. We set N = r and use the letter r to avoid confusion.
$f(x_1,\ldots,x_g)$ of fixed degree. We are free to choose N, and we will always take it to be an odd prime number. We set N = r and use the letter r to avoid confusion.
The following lemma is a version of the well-known Schwartz–Zippel bound. Notice that a polynomial in g variables having degree at most d in each of them has total degree at most dg.
Lemma 6.2. Let ![]() $g,d$ be natural numbers with
$g,d$ be natural numbers with ![]() $g \ge 1$, let r be a prime number and let
$g \ge 1$, let r be a prime number and let ![]() $f(x_1,\ldots,x_g) \in \mathbb{F}_r[x_1,\ldots,x_g]$ be a non-zero polynomial of degree
$f(x_1,\ldots,x_g) \in \mathbb{F}_r[x_1,\ldots,x_g]$ be a non-zero polynomial of degree ![]() $\le d$ in each variable. We have
$\le d$ in each variable. We have
 \begin{equation*}
\# \{(u_1,\ldots,u_g) \in \mathbb{F}_r^g \mid f(u_1,\ldots,u_g)=0 \} \le dg \cdot r^{g-1}.
\end{equation*}
\begin{equation*}
\# \{(u_1,\ldots,u_g) \in \mathbb{F}_r^g \mid f(u_1,\ldots,u_g)=0 \} \le dg \cdot r^{g-1}.
\end{equation*} Next, we identify the set of characteristic polynomials of matrices in  $\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$. We show the following more general result:
$\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$. We show the following more general result:
Proposition 6.3. Let n be a positive integer, let R be a commutative ring with 1, and let ![]() $q \in R^\times$. Let
$q \in R^\times$. Let ![]() $p(x) = a_0 + a_1 x + \cdots + a_{2n} x^{2n} \in R[x]$ be a monic polynomial satisfying
$p(x) = a_0 + a_1 x + \cdots + a_{2n} x^{2n} \in R[x]$ be a monic polynomial satisfying ![]() $a_{n-i}=q^i a_{n+i}$ for all
$a_{n-i}=q^i a_{n+i}$ for all ![]() $i=0,\ldots,n$. There exists
$i=0,\ldots,n$. There exists ![]() $M \in \operatorname{GSp}_{2n}(R)$ with multiplier q and characteristic polynomial p(x).
$M \in \operatorname{GSp}_{2n}(R)$ with multiplier q and characteristic polynomial p(x).
Remark 6.4. The statement is a simple variant of [Reference Rivin45, theorem A.1]. We give a detailed argument since, unfortunately, the proof of [Reference Rivin45, theorem A.1] seems to contain some typos. For example, in op. cit., the matrix B is declared to have determinant 1, but the construction does not ensure this property; more importantly, in some examples we tried, the given construction does not seem to yield matrices with the claimed characteristic polynomials. Our construction is therefore slightly different from that of [Reference Rivin45, theorem A.1], which we could not fully understand.
Proof. We work with the symplectic form given by the matrix  $J=\begin{pmatrix}
0 & \operatorname{Id}_n \\
-\operatorname{Id}_n & 0
\end{pmatrix}$. We construct the desired M as a block-matrix
$J=\begin{pmatrix}
0 & \operatorname{Id}_n \\
-\operatorname{Id}_n & 0
\end{pmatrix}$. We construct the desired M as a block-matrix  $M=\begin{pmatrix}
0 & B \\ C & D
\end{pmatrix}$, where B, C, D satisfy the following:
$M=\begin{pmatrix}
0 & B \\ C & D
\end{pmatrix}$, where B, C, D satisfy the following:
1.
 $B, C, D$ are square n × n matrices with B invertible;
$B, C, D$ are square n × n matrices with B invertible;2. B is the symmetric matrix
 \begin{equation*}
B= \begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 1 \\
0 & 0 & 0 & \cdots & 1 & b_2 \\
0 & 0 & 0 & \cdots & b_2 & b_3 \\
&&& \unicode{x22F0}\\
0 & 1 & b_2 & \cdots & b_{n-2} & b_{n-1} \\
1 & b_2 & b_3 & \cdots & b_{n-1} & b_n \\
\end{pmatrix},
\end{equation*}
\begin{equation*}
B= \begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 1 \\
0 & 0 & 0 & \cdots & 1 & b_2 \\
0 & 0 & 0 & \cdots & b_2 & b_3 \\
&&& \unicode{x22F0}\\
0 & 1 & b_2 & \cdots & b_{n-2} & b_{n-1} \\
1 & b_2 & b_3 & \cdots & b_{n-1} & b_n \\
\end{pmatrix},
\end{equation*}or, in symbols,
 \begin{equation*}
B_{ij}= b_{i+j-n} \delta_{i+j \geq n+1} = \begin{cases}
0, \text{if } i+j \leq n \\
1, \text{if } i+j = n+1 \\
b_{i+j-n}, \text{if } i+j \gt n+1,
\end{cases}
\end{equation*}
\begin{equation*}
B_{ij}= b_{i+j-n} \delta_{i+j \geq n+1} = \begin{cases}
0, \text{if } i+j \leq n \\
1, \text{if } i+j = n+1 \\
b_{i+j-n}, \text{if } i+j \gt n+1,
\end{cases}
\end{equation*}where we have set
 $b_1=1$ and
$b_1=1$ and  $\delta_{i+j \geq n+1} = \begin{cases}
1, \text{if } i+j \geq n+1 \\
0, \text{otherwise.}
\end{cases}$. Note that any matrix B of this form is invertible for any choice of the bi;
$\delta_{i+j \geq n+1} = \begin{cases}
1, \text{if } i+j \geq n+1 \\
0, \text{otherwise.}
\end{cases}$. Note that any matrix B of this form is invertible for any choice of the bi;3.
 $C = -q ({}^tB)^{-1} = -q B^{-1}$;
$C = -q ({}^tB)^{-1} = -q B^{-1}$;4. D is the companion matrix given by
 $D=\begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 0 & d_1 \\
1 & 0 & 0 & \cdots & 0 & 0 & d_2 \\
& & & \ddots & & \\
0 & 0 & 0 & \cdots & 0 & 0 & d_{n-2} \\
0 & 0 & 0 & \cdots & 1 & 0 &d_{n-1} \\
0 & 0 & 0 & \cdots & 0 & 1 & d_n \\
\end{pmatrix}$. In symbols,
$D=\begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 0 & d_1 \\
1 & 0 & 0 & \cdots & 0 & 0 & d_2 \\
& & & \ddots & & \\
0 & 0 & 0 & \cdots & 0 & 0 & d_{n-2} \\
0 & 0 & 0 & \cdots & 1 & 0 &d_{n-1} \\
0 & 0 & 0 & \cdots & 0 & 1 & d_n \\
\end{pmatrix}$. In symbols,
 \begin{equation*}
D_{ij} = \begin{cases}
1, \text{if } i=j+1 \\
d_i, \text{if } j=n \\
0, \text{otherwise.}
\end{cases}
\end{equation*}
\begin{equation*}
D_{ij} = \begin{cases}
1, \text{if } i=j+1 \\
d_i, \text{if } j=n \\
0, \text{otherwise.}
\end{cases}
\end{equation*}
Here ![]() $b_2, \ldots, b_n \in R$ and
$b_2, \ldots, b_n \in R$ and ![]() $d_1, \ldots, d_n \in R$ are coefficients to be chosen later. We check the conditions for the matrix M to be symplectic with multiplier q. We compute
$d_1, \ldots, d_n \in R$ are coefficients to be chosen later. We check the conditions for the matrix M to be symplectic with multiplier q. We compute
 \begin{equation*}
{}^t M J M = \begin{pmatrix}
0 & -{}^tC B \\ {}^tB C & {}^t B D - {}^tD B
\end{pmatrix},
\end{equation*}
\begin{equation*}
{}^t M J M = \begin{pmatrix}
0 & -{}^tC B \\ {}^tB C & {}^t B D - {}^tD B
\end{pmatrix},
\end{equation*}which is equal to qJ if and only if
 \begin{equation*}
\begin{cases}
-{}^tC B = q\operatorname{Id} \\
{}^tB C = -q\operatorname{Id} \\
{}^t B D - {}^tD B = 0.
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
-{}^tC B = q\operatorname{Id} \\
{}^tB C = -q\operatorname{Id} \\
{}^t B D - {}^tD B = 0.
\end{cases}
\end{equation*} The first two equations are equivalent to one another and automatically satisfied by our choice of C. The third equation is equivalent to the matrix ![]() ${}^tB D = BD$ being symmetric. We claim that this is achieved by taking (
${}^tB D = BD$ being symmetric. We claim that this is achieved by taking (![]() $b_1=1$ and)
$b_1=1$ and)  $b_{k+1} = \sum_{i=1}^k b_i d_{n+i-k}$ for
$b_{k+1} = \sum_{i=1}^k b_i d_{n+i-k}$ for ![]() $k=1,\ldots,n-1$ (notice that d 1 does not occur). Indeed, the first n − 1 columns of the product BD are given by the second, third,
$k=1,\ldots,n-1$ (notice that d 1 does not occur). Indeed, the first n − 1 columns of the product BD are given by the second, third, ![]() $\ldots$, nth column of B, while the last one is the linear combination
$\ldots$, nth column of B, while the last one is the linear combination ![]() $d_1 B^1 + d_2 B^2 + \cdots + d_n B^n$, where we denote by Bi the ith column of B. From this, it is immediate to check that the top-left block of BD of size
$d_1 B^1 + d_2 B^2 + \cdots + d_n B^n$, where we denote by Bi the ith column of B. From this, it is immediate to check that the top-left block of BD of size ![]() $(n-1) \times (n-1)$ is symmetric (independently of the values of
$(n-1) \times (n-1)$ is symmetric (independently of the values of ![]() $b_2, \ldots, b_n, d_1, \ldots, d_n$), and we only need to impose that the last line of BD is equal to (the transpose of) its last column. We can also ignore the coefficient in position (n, n), so we compare the first n − 1 coefficients of the last line of BD with the first n − 1 coefficients of its last column. The kth coefficient on the last line is the coefficient on the last line of the
$b_2, \ldots, b_n, d_1, \ldots, d_n$), and we only need to impose that the last line of BD is equal to (the transpose of) its last column. We can also ignore the coefficient in position (n, n), so we compare the first n − 1 coefficients of the last line of BD with the first n − 1 coefficients of its last column. The kth coefficient on the last line is the coefficient on the last line of the ![]() $(k+1)$th column of B, that is,
$(k+1)$th column of B, that is, ![]() $b_{k+1}$. The kth coefficient on the last column is given by
$b_{k+1}$. The kth coefficient on the last column is given by
 \begin{align*}
d_1 B_{k1} + d_2 B_{k2} + \cdots + d_n B_{kn} &= \sum_{i=1}^n d_i B_{ki} = \sum_{i=1}^n d_i \delta_{k+i \geq n+1} b_{k+i-n} \\
&=
\sum_{i'=1}^{k} b_{i'} d_{i'+n-k}.
\end{align*}
\begin{align*}
d_1 B_{k1} + d_2 B_{k2} + \cdots + d_n B_{kn} &= \sum_{i=1}^n d_i B_{ki} = \sum_{i=1}^n d_i \delta_{k+i \geq n+1} b_{k+i-n} \\
&=
\sum_{i'=1}^{k} b_{i'} d_{i'+n-k}.
\end{align*} Thus, the symmetry condition is satisfied if and only if for ![]() $k=1,\ldots,n-1$ we have
$k=1,\ldots,n-1$ we have  $b_{k+1} = \sum_{i=1}^{k} b_{i} d_{n+i-k}$, as claimed. Also note that a symplectic matrix with invertible multiplier is itself invertible (because the determinant of a symplectic matrix is a power of its multiplier), so M is invertible and therefore an element of
$b_{k+1} = \sum_{i=1}^{k} b_{i} d_{n+i-k}$, as claimed. Also note that a symplectic matrix with invertible multiplier is itself invertible (because the determinant of a symplectic matrix is a power of its multiplier), so M is invertible and therefore an element of ![]() $\operatorname{GSp}_{2n}(R)$. In particular, for any choice of
$\operatorname{GSp}_{2n}(R)$. In particular, for any choice of ![]() $d_1, \ldots, d_n$, we have constructed a corresponding matrix M that is symplectic of multiplier q and has D as its bottom-right block of size n × n. We now compute the characteristic polynomial of this matrix M. Consider the identity
$d_1, \ldots, d_n$, we have constructed a corresponding matrix M that is symplectic of multiplier q and has D as its bottom-right block of size n × n. We now compute the characteristic polynomial of this matrix M. Consider the identity
 \begin{equation*}
\begin{aligned}
\begin{pmatrix}
x\operatorname{Id}_n & -B \\
-C & x\operatorname{Id}_n-D
\end{pmatrix} \begin{pmatrix}
B & 0 \\
x \operatorname{Id}_n & B^{-1}
\end{pmatrix} & = \begin{pmatrix}
0 & -\operatorname{Id}_n \\
x^2 \operatorname{Id}_n -xD -CB & x B^{-1}-DB^{-1}
\end{pmatrix} \\ & = \begin{pmatrix}
0 & -\operatorname{Id}_n \\
(x^2+q) \operatorname{Id}_n -xD & x B^{-1}-DB^{-1}
\end{pmatrix},
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\begin{pmatrix}
x\operatorname{Id}_n & -B \\
-C & x\operatorname{Id}_n-D
\end{pmatrix} \begin{pmatrix}
B & 0 \\
x \operatorname{Id}_n & B^{-1}
\end{pmatrix} & = \begin{pmatrix}
0 & -\operatorname{Id}_n \\
x^2 \operatorname{Id}_n -xD -CB & x B^{-1}-DB^{-1}
\end{pmatrix} \\ & = \begin{pmatrix}
0 & -\operatorname{Id}_n \\
(x^2+q) \operatorname{Id}_n -xD & x B^{-1}-DB^{-1}
\end{pmatrix},
\end{aligned}
\end{equation*} where we have used that—by definition—![]() $CB=-q\operatorname{Id}$. Taking determinants on both sides and using that the determinant of the block-matrix
$CB=-q\operatorname{Id}$. Taking determinants on both sides and using that the determinant of the block-matrix  $\begin{pmatrix}
B & 0 \\
x \operatorname{Id} & B^{-1}
\end{pmatrix}$ is 1, we obtain
$\begin{pmatrix}
B & 0 \\
x \operatorname{Id} & B^{-1}
\end{pmatrix}$ is 1, we obtain
 \begin{align*}
&\det(x\operatorname{Id}_{2n} - M) = \det \begin{pmatrix}
0 & -\operatorname{Id}_n \\
(x^2+q) \operatorname{Id}_n -xD & x B^{-1}-DB^{-1}
\end{pmatrix} \\
&= \det((x^2+q) \operatorname{Id}_n -xD),
\end{align*}
\begin{align*}
&\det(x\operatorname{Id}_{2n} - M) = \det \begin{pmatrix}
0 & -\operatorname{Id}_n \\
(x^2+q) \operatorname{Id}_n -xD & x B^{-1}-DB^{-1}
\end{pmatrix} \\
&= \det((x^2+q) \operatorname{Id}_n -xD),
\end{align*}where the last equality uses basic properties of the determinant of block matrices. Finally, we can rewrite this in the form
 \begin{equation*}
\det(x\operatorname{Id}_{2n} - M) = x^n \det\left( \left(x + \frac{q}{x}\right) \operatorname{Id}_n - D\right),
\end{equation*}
\begin{equation*}
\det(x\operatorname{Id}_{2n} - M) = x^n \det\left( \left(x + \frac{q}{x}\right) \operatorname{Id}_n - D\right),
\end{equation*} so the characteristic polynomial of M is equal to  $x^np_D\left(x+\frac{q}{x} \right)$, where
$x^np_D\left(x+\frac{q}{x} \right)$, where ![]() $p_D(x)$ is the characteristic polynomial of D. To conclude the proof, it suffices to show that we can choose D in such a way that
$p_D(x)$ is the characteristic polynomial of D. To conclude the proof, it suffices to show that we can choose D in such a way that  $x^np_D\left(x+\frac{q}{x} \right)=p(x)$, where p(x) is the polynomial given in the statement. This is easy: D is a companion matrix, so any monic polynomial with coefficients in R can be realized as
$x^np_D\left(x+\frac{q}{x} \right)=p(x)$, where p(x) is the polynomial given in the statement. This is easy: D is a companion matrix, so any monic polynomial with coefficients in R can be realized as ![]() $p_D(x)$ for suitable values of
$p_D(x)$ for suitable values of ![]() $d_1, \ldots, d_n$. Finally, it is an easy exercise to show that a monic polynomial
$d_1, \ldots, d_n$. Finally, it is an easy exercise to show that a monic polynomial  $p(x) = \sum_{i=0}^{2n} a_i x^i$ that satisfies
$p(x) = \sum_{i=0}^{2n} a_i x^i$ that satisfies ![]() $a_{n-i}=q^ia_{n+i}$ for all
$a_{n-i}=q^ia_{n+i}$ for all ![]() $i=0,\ldots,n$ can be written as
$i=0,\ldots,n$ can be written as  $x^n p_1\left( x + \frac{q}{x}\right)$ for some monic polynomial
$x^n p_1\left( x + \frac{q}{x}\right)$ for some monic polynomial ![]() $p_1 \in R[x]$ of degree n.
$p_1 \in R[x]$ of degree n.
Remark 6.5. Inspection of the proof shows that the following slightly stronger statement is true for the case of R being the fraction field of a domain A: if the characteristic polynomial p(x) has coefficients in A and ![]() $q \in A$, then we may choose M to have coefficients in A, even if the multiplier q is not invertible in A. This applies in particular when
$q \in A$, then we may choose M to have coefficients in A, even if the multiplier q is not invertible in A. This applies in particular when ![]() $A=\mathbb{Z}_\ell$ and
$A=\mathbb{Z}_\ell$ and ![]() $R=\mathbb{Q}_\ell$.
$R=\mathbb{Q}_\ell$.
Corollary 6.6. Let r be a prime and let q be an integer prime to r. The set  $\{\operatorname{charpol} M : M \in \operatorname{GSp}_{2g}^q(\mathbb{F}_r) \}$ has cardinality r g.
$\{\operatorname{charpol} M : M \in \operatorname{GSp}_{2g}^q(\mathbb{F}_r) \}$ has cardinality r g.
Proof. By proposition 6.3, the set in question is the set of all monic polynomials in ![]() $\mathbb{F}_r[x]$ of degree 2g whose coefficients ai satisfy
$\mathbb{F}_r[x]$ of degree 2g whose coefficients ai satisfy ![]() $a_{g-i}=q^ia_{g+i}$ for all
$a_{g-i}=q^ia_{g+i}$ for all ![]() $i=0,\ldots,g$. Since any choice of the coefficients
$i=0,\ldots,g$. Since any choice of the coefficients ![]() $a_1, \ldots, a_g$ corresponds to precisely one such polynomial, the total number of polynomials is rg.
$a_1, \ldots, a_g$ corresponds to precisely one such polynomial, the total number of polynomials is rg.
Finally, we connect characteristic polynomials of matrices in  $\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$ with characteristic polynomials of Frobenius:
$\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$ with characteristic polynomials of Frobenius:
Lemma 6.7. Let ![]() $g,r$ be positive integers. There is a constant
$g,r$ be positive integers. There is a constant ![]() $h_{g,r}$ such that for any prime power
$h_{g,r}$ such that for any prime power ![]() $q \gt h_{g,r}$ with
$q \gt h_{g,r}$ with ![]() $(q,r)=1$ and for any element M of
$(q,r)=1$ and for any element M of  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$, there is a curve
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$, there is a curve ![]() $C \in \mathcal{M}_g(\mathbb{F}_q)$ such that the reduction of
$C \in \mathcal{M}_g(\mathbb{F}_q)$ such that the reduction of ![]() $f_{C}(t)$ modulo r is the characteristic polynomial of M.
$f_{C}(t)$ modulo r is the characteristic polynomial of M.
Proof. This is an immediate consequence of results of Katz–Sarnak [Reference Katz and Sarnak29]. We give a proof in the language of this article.
For g = 1, the result follows from the fact that (writing ![]() $q=p^n$) every polynomial of the form
$q=p^n$) every polynomial of the form ![]() $t^2+at+q$ with
$t^2+at+q$ with ![]() $p \nmid a$ and
$p \nmid a$ and ![]() $|a| \leq 2\sqrt{q}$ is the L-polynomial of an elliptic curve over
$|a| \leq 2\sqrt{q}$ is the L-polynomial of an elliptic curve over ![]() $\mathbb{F}_q$ (see [Reference Waterhouse50, theorem 4.1]). Consider first the prime powers
$\mathbb{F}_q$ (see [Reference Waterhouse50, theorem 4.1]). Consider first the prime powers ![]() $q=p^n$ for which p satisfies
$q=p^n$ for which p satisfies ![]() $p \gt 2\sqrt{p} \gt r$. The integers
$p \gt 2\sqrt{p} \gt r$. The integers ![]() $a=1, \ldots, r$ realize all the residue classes modulo r, are not divisible by p, and satisfy
$a=1, \ldots, r$ realize all the residue classes modulo r, are not divisible by p, and satisfy ![]() $|a| \leq 2\sqrt{q}$, so the corresponding polynomials
$|a| \leq 2\sqrt{q}$, so the corresponding polynomials ![]() $t^2+at+q$ are all realized by elliptic curves over
$t^2+at+q$ are all realized by elliptic curves over ![]() $\mathbb{F}_q$ and give all the characteristic polynomials of elements in
$\mathbb{F}_q$ and give all the characteristic polynomials of elements in  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$. Consider now the prime powers
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$. Consider now the prime powers ![]() $q=p^n$ for the finitely many primes p that safisfy
$q=p^n$ for the finitely many primes p that safisfy ![]() $2\sqrt{p} \leq r$ or
$2\sqrt{p} \leq r$ or ![]() $p \leq 2\sqrt{p}$, with
$p \leq 2\sqrt{p}$, with ![]() $(p,r)=1$. Suppose that
$(p,r)=1$. Suppose that ![]() $\lfloor 2\sqrt{q} \rfloor \geq pr$, which holds for all n large enough (with respect to p). The integers
$\lfloor 2\sqrt{q} \rfloor \geq pr$, which holds for all n large enough (with respect to p). The integers ![]() $1, \ldots, \lfloor 2\sqrt{q} \rfloor$ cover all residue classes modulo pr, hence in particular for every residue class modulo r there is
$1, \ldots, \lfloor 2\sqrt{q} \rfloor$ cover all residue classes modulo pr, hence in particular for every residue class modulo r there is ![]() $a \in \{1, \ldots, \lfloor 2\sqrt{q} \rfloor\}$ that realizes the given class modulo r and is not divisible by p (recall that
$a \in \{1, \ldots, \lfloor 2\sqrt{q} \rfloor\}$ that realizes the given class modulo r and is not divisible by p (recall that ![]() $(p,r)=1$). As above,
$(p,r)=1$). As above, ![]() $t^2+at+q$ is the L-polynomial of an elliptic curve over
$t^2+at+q$ is the L-polynomial of an elliptic curve over ![]() $\mathbb{F}_q$, and we are done.
$\mathbb{F}_q$, and we are done.
For ![]() $g \geq 2$, the result follows from theorem 2.1, as we now show. Let p(t) be the characteristic polynomial of M. Notice that
$g \geq 2$, the result follows from theorem 2.1, as we now show. Let p(t) be the characteristic polynomial of M. Notice that ![]() $\mu_r^q$ gives positive mass to the singleton
$\mu_r^q$ gives positive mass to the singleton ![]() $\{p(t)\}$, since
$\{p(t)\}$, since  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$ is a finite set. In fact, since the cardinality of
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$ is a finite set. In fact, since the cardinality of  $\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$ is independent of q (it is equal to
$\operatorname{GSp}_{2g}^q(\mathbb{Z}/r\mathbb{Z})$ is independent of q (it is equal to ![]() $\#\operatorname{Sp}_{2g}(\mathbb{Z}/r\mathbb{Z})$, provided only that
$\#\operatorname{Sp}_{2g}(\mathbb{Z}/r\mathbb{Z})$, provided only that ![]() $(q,r)=1$), we have
$(q,r)=1$), we have ![]() $\mu_r^q \{p(t)\} \geq c_{g,r} \gt 0$ for some absolute constant
$\mu_r^q \{p(t)\} \geq c_{g,r} \gt 0$ for some absolute constant ![]() $c_{g,r}$. By theorem 2.1, this implies that
$c_{g,r}$. By theorem 2.1, this implies that  $(\operatorname{charpol}_r)_* \mathbb{P}^{\operatorname{naive}}_{g, q}$ is positive at
$(\operatorname{charpol}_r)_* \mathbb{P}^{\operatorname{naive}}_{g, q}$ is positive at ![]() $\{p(t)\}$ for q large enough. Repeating the argument for the finitely many possible polynomials p(t) concludes the proof.
$\{p(t)\}$ for q large enough. Repeating the argument for the finitely many possible polynomials p(t) concludes the proof.
We can now combine our bounds to conclude the proof of theorem 6.1.
Proof of theorem 6.1
Let r be an odd prime number, which will later be required to be large enough. We prove the result for every q which is not a power of r; repeating the argument with a different r will prove the statement for every q. First, we can assume that our polynomial ![]() $f(x_1,\ldots,x_g) \in \mathbb{Z}[x_1,\ldots,x_g]$ has a coefficient which is non-zero modulo r (otherwise, divide by an appropriate power of r). Hence, its reduction modulo r is non-zero. By lemma 6.7, the set of characteristic polynomials of curves in
$f(x_1,\ldots,x_g) \in \mathbb{Z}[x_1,\ldots,x_g]$ has a coefficient which is non-zero modulo r (otherwise, divide by an appropriate power of r). Hence, its reduction modulo r is non-zero. By lemma 6.7, the set of characteristic polynomials of curves in ![]() $\mathcal{M}_g(\mathbb{F}_q)$ modulo r is the same as the set of characteristic polynomials of matrices of
$\mathcal{M}_g(\mathbb{F}_q)$ modulo r is the same as the set of characteristic polynomials of matrices of  $\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$ for q large enough and relatively prime with r. Suppose that for every
$\operatorname{GSp}_{2g}^q(\mathbb{F}_r)$ for q large enough and relatively prime with r. Suppose that for every  $M \in \operatorname{GSp}_{2g}^q(\mathbb{F}_r)$, writing
$M \in \operatorname{GSp}_{2g}^q(\mathbb{F}_r)$, writing  $\operatorname{charpol}(M)=\sum_{i=0}^{2g} a_i t^i$, we have
$\operatorname{charpol}(M)=\sum_{i=0}^{2g} a_i t^i$, we have ![]() $f(a_1,\ldots,a_g)=0$. By combining lemma 6.2 and corollary 6.6 we obtain
$f(a_1,\ldots,a_g)=0$. By combining lemma 6.2 and corollary 6.6 we obtain ![]() $
r^g \le dg \cdot r^{g-1},
$ which implies
$
r^g \le dg \cdot r^{g-1},
$ which implies ![]() $r \le dg$. If r is chosen larger than this quantity, we obtain a contradiction.
$r \le dg$. If r is chosen larger than this quantity, we obtain a contradiction.
Acknowledgements
We thank Umberto Zannier for bringing the problem to our attention, for many useful suggestions, and especially for pointing out the relevance of the equidistribution results of Katz–Sarnak, noting that they imply the case ![]() $q \gg_g 0$ of theorem 1.4. In addition, the first author would like to thank Umberto Zannier for his guidance during his undergraduate studies, on a topic that ultimately inspired much of the work in this article. We are grateful to J. Kaczorowski and A. Perelli for sharing their work [Reference Kaczorowski and Perelli28] before publication. We thank Christophe Ritzenthaler and Elisa Lorenzo García for their interesting comments on the first version of this article, Zhao Yu Ma for a comment about remark 3.12, and the anonymous referees for their helpful suggestions.
$q \gg_g 0$ of theorem 1.4. In addition, the first author would like to thank Umberto Zannier for his guidance during his undergraduate studies, on a topic that ultimately inspired much of the work in this article. We are grateful to J. Kaczorowski and A. Perelli for sharing their work [Reference Kaczorowski and Perelli28] before publication. We thank Christophe Ritzenthaler and Elisa Lorenzo García for their interesting comments on the first version of this article, Zhao Yu Ma for a comment about remark 3.12, and the anonymous referees for their helpful suggestions.