This work presents a $\textsf{Python}$ EMD package named AdvEMDpy that is both more flexible and generalises existing empirical mode decomposition (EMD) packages in $\textsf{Python}$, $\textsf{R}$, and $\textsf{MATLAB}$. It is aimed specifically for use by the insurance and financial risk communities, for applications such as return modelling, claims modelling, and life insurance applications with a particular focus on mortality modelling. AdvEMDpy both expands upon the EMD options and methods available, and improves their statistical robustness and efficiency, providing a robust, usable, and reliable toolbox. Unlike many EMD packages, AdvEMDpy allows customisation by the user, to ensure that a broader class of linear, non-linear, and non-stationary time series analyses can be performed. The intrinsic mode functions (IMFs) extracted using EMD contain complex multi-frequency structures which warrant maximum algorithmic customisation for effective analysis. A major contribution of this package is the intensive treatment of the EMD edge effect which is the most ubiquitous problem in EMD and time series analysis. Various EMD techniques, of varying intricacy from numerous works, have been developed, refined, and, for the first time, compiled in AdvEMDpy. In addition to the EMD edge effect, numerous pre-processing, post-processing, detrended fluctuation analysis (localised trend estimation) techniques, stopping criteria, spline methods, discrete-time Hilbert transforms (DTHT), knot point optimisations, and other algorithmic variations have been incorporated and presented to the users of AdvEMDpy. This paper and the supplementary materials provide several real-world actuarial applications of this package for the user’s benefit.

The aim of this paper is to characterize the non-negative functions φ defined on (0,∞) for which the Hausdorff operator

$${\rm {\cal H}}_\varphi f(z) = \int_0^\infty f \left( {\displaystyle{z \over t}} \right)\displaystyle{{\varphi (t)} \over t}{\rm d}t$$

${\rm {\cal H}}_a^p ({\open C}_ + )$

$p\in [1,\infty ]$

In this paper we study the Hilbert transformations over ${{L}^{2}}(\mathbb{R})$ and ${{L}^{2}}(\mathbb{T})$ from the viewpoint of symmetry. For a linear operator over ${{L}^{2}}(\mathbb{R})$ commutative with the $ax\,+\,b$ group, we show that the operator is of the form $\lambda I+\eta H$, where $I$ and $H$ are the identity operator and Hilbert transformation, respectively, and $\lambda ,\eta $ are complex numbers. In the related literature this result was proved by first invoking the boundedness result of the operator using some machinery. In our setting the boundedness is a consequence of the boundedness of the Hilbert transformation. The methodology that we use is the Gelfand–Naimark representation of the $ax\,+\,b$ group. Furthermore, we prove a similar result on the unit circle. Although there does not exist a group like the $ax\,+\,b$ group on the unit circle, we construct a semigroup that plays the same symmetry role for the Hilbert transformations over the circle ${{L}^{2}}(\mathbb{T})$.

A diode-pumped alkali vapor laser (DPAL) is one of the most promising candidates of the next-generation high-powered laser source. As the saturated number density of alkali vapor is highly dependent on the temperature inside a vapor cell, the temperature distribution in the cross-section of a cell will greatly affect the homogeneity of a laser medium and the output characteristics of a DPAL. In this paper, we developed an algorithm based on the regime concluding quasi-Hilbert transform to evaluate the phase aberration of a wavefront when the probe beam passes through the vapor cell placed in one arm of a Mach–Zehnder interference setup. According to the theoretical algorithm, we deduced the temperature distribution of a cesium vapor cell for different heating conditions. The study is thought to be useful for development of a high-powered laser.

We raise a question of whether the Riesz transform on $\mathbb{T}^{n}$ or $\mathbb{Z}^{n}$ is characterized by the ‘maximal semigroup symmetry’ that the transform satisfies. We prove that this is the case if and only if the dimension is one, two or a multiple of four. This generalizes a theorem of Edwards and Gaudry for the Hilbert transform on $\mathbb{T}$ and $\mathbb{Z}$ in the one-dimensional case, and extends a theorem of Stein for the Riesz transform on $\mathbb{R}^{n}$. Unlike the $\mathbb{R}^{n}$ case, we show that there exist infinitely many linearly independent multiplier operators that enjoy the same maximal semigroup symmetry as the Riesz transforms on $\mathbb{T}^{n}$ and $\mathbb{Z}^{n}$ if the dimension $n$ is greater than or equal to three and is not a multiple of four.

The early detection of gear faults remains a major problem, especially when the gears aresubjected to non stationary phenomena due to defects. In industrial applications, thecrack of tooth is a default very difficult to detect whether using the time descriptors orthe frequency analysis. In this work and based on a numerical model, we prove that thecrack default affects directly the phase of the frequency component of the defective wheel(frequency modulation). To properly estimate the phases, we suggest two high-resolutiontechniques (Estimation of Signal Parameters via Rotational Invariance Techniques ESPRITwith a sliding window and Weighted Least Squares Estimator WLSE). The results of bothmethods are compared to the phase obtained by Hilbert transform. The three techniques arethen applied on a multiplicative signal with a frequency modulation to show the influenceof the amplitude modulation on the quality of phase estimation. We note that the ESPRITmethod is much better in the estimation of frequencies while WLSE shows much efficiency inthe estimation of phases if we keep the frequencies almost stables.

In recent years, the adaptive decomposition methods have become the center of interest of researchers in many fields and especially in the vibration diagnosis of rotating machines. This paper compares the sensitivity of defect detection of two adaptive methods: local mean decomposition (L.M.D) and empirical mode decomposition (E.M.D). The efficiency of L.M.D and E.M.D methods for detecting defects is investigated for two cases, one from numerical signals and the other from signals recorded during a fatigue test on gear bench. The time descriptors Kurtosis, Thalaf and Thikat are applied on the signal and on its Hilbert transform. The results reveal that both techniques seem to be suitable and have good efficiency for the fault detection. From experimental signals, the comparative results reveal that both methods allow for monitoring wear, but that L.M.D is more sensitive to detect rapid changes of degradation than E.M.D method for the considered case. Consequently these features have potential to become powerful tools for the monitoring of rotating machinery.

We inspect the relationship between relative Fourier multipliers on noncommutative Lebesgue–Orlicz spaces of a discrete group $\Gamma$ and relative Toeplitz-Schur multipliers on Schatten–von-Neumann–Orlicz classes. Four applications are given: lacunary sets, unconditional Schauder bases for the subspace of a Lebesgue space determined by a given spectrum $\Lambda \,\subseteq \,\Gamma$, the norm of the Hilbert transformand the Riesz projection on Schatten–von-Neumann classes with exponent a power of 2, and the norm of Toeplitz Schur multipliers on Schatten–von-Neumann classes with exponent less than 1.

For a class of convex curves in ℝd we prove that the corresponding maximal operator and Hilbert transform are of weak type Llog L. The point of interest here is that this class admits curves which are infinitely flat at the origin. We also prove an analogous weak type result for a class of nonconvex hypersurfaces.

It is shown that the ergodic Hilbert transform exists for a class of bounded symmetric admissible processes relative to invertible measure preserving transformations. This generalizes the well-known result on the existence of the ergodic Hilbert transform.

A model subspace ${{K}_{\Theta }}$ of the Hardy space ${{H}^{2}}={{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)$ for the upper half plane ${{\mathbb{C}}_{+}}$ is ${{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)\ominus \Theta {{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)$ where $\Theta $ is an inner function in ${{\mathbb{C}}_{+}}$. A function $\omega :\,\mathbb{R}\mapsto [0,\,\infty )$ is called an admissible majorant for ${{K}_{\Theta }}$ if there exists an $f\,\in \,{{K}_{\Theta }},\,f\,\not{\equiv }\,0,\,|f\left( x \right)|\,\le \,\omega \left( x \right)$ almost everywhere on $\mathbb{R}$. For some (mainly meromorphic) $\Theta $'s some parts of Adm $\Theta $ (the set of all admissible majorants for ${{K}_{\Theta }}$) are explicitly described. These descriptions depend on the rate of growth of arg $\Theta $ along $\mathbb{R}$. This paper is about slowly growing arguments (slower than $x$). Our results exhibit the dependence of Adm $B$ on the geometry of the zeros of the Blaschke product $B$. A complete description of Adm $B$ is obtained for $B$'s with purely imaginary (“vertical”) zeros. We show that in this case a unique minimal admissible majorant exists.

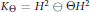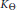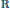This paper is a continuation of $[6]$. We consider the model subspaces ${{K}_{\Theta }}={{H}^{2}}\ominus \Theta {{H}^{2}}$ of the Hardy space ${{H}^{2}}$ generated by an inner function $\Theta $ in the upper half plane. Our main object is the class of admissible majorants for ${{K}_{\Theta }}$, denoted by Adm $\Theta $ and consisting of all functions $\omega $ defined on $\mathbb{R}$ such that there exists an 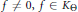$f\ne 0,f\in {{K}_{\Theta }}$ satisfying $|f\left( x \right)|\,\le \,\omega \left( x \right)$ almost everywhere on 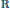$\mathbb{R}$. Firstly, using some simple Hilbert transform techniques, we obtain a general multiplier theorem applicable to any 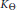${{K}_{\Theta }}$ generated by a meromorphic inner function. In contrast with 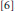$[6]$, we consider the generating functions $\Theta $ such that the unit vector 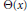$\Theta \left( x \right)$ winds up fast as $x$ grows from $-\infty \,\text{to}\,\infty $. In particular, we consider $\Theta \,=\,B$ where $B$ is a Blaschke product with “horizontal” zeros, i.e., almost uniformly distributed in a strip parallel to and separated from 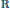$\mathbb{R}$. It is shown, among other things, that for any such 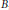$B$, any even $\omega $ decreasing on 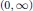$\left( 0,\,\infty \right)$ with a finite logarithmic integral is in Adm 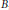$B$ (unlike the “vertical” case treated in 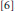$[6]$), thus generalizing (with a new proof) a classical result related to Adm $\exp \left( i\sigma z \right),\,\sigma \,>\,0$. Some oscillating $\omega $'s in Adm 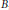$B$ are also described. Our theme is related to the Beurling-Malliavin multiplier theorem devoted to Adm $\exp \left( i\sigma z \right),\,\sigma \,>\,0$, and to de Branges’ space 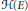$H\left( E \right)$.

We consider Hilbert transforms along curves $\Gamma$ on the Heisenberg group. In particular, necessary and sufficient conditions for the $L^2$-boundedness are given for $\Gamma(t)=(t,\gamma(t),0)$ when $\gamma$ is even or odd and convex on ${\Bbb R}^{+}$. 1991 Mathematics Subject Classification: 42B20,42B25.

A distributional solution to the Hilbert problem in dimension > 1 is given.