Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T18:21:24.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert Transformation and Representation of the ax + b Group

Published online by Cambridge University Press:  20 November 2018

Pei Dang ,
Hua Liu  and
Tao Qian
Pei Dang
Affiliation:
Faculty of Information Technology, Macau University of Science and Technology, Macau, China, e-mail: pdang@must.edu.mo
Hua Liu
Affiliation:
Department of Mathematics, Tianjin University of Technology and Education, Tianjin 300222, China, e-mail: daliuhua@163.com
Tao Qian
Affiliation:
Department of Mathematics, University of Macau, Macau, China, e-mail: fsttq@umac.mo
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the Hilbert transformations over 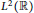${{L}^{2}}(\mathbb{R})$ and 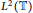${{L}^{2}}(\mathbb{T})$ from the viewpoint of symmetry. For a linear operator over 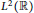${{L}^{2}}(\mathbb{R})$ commutative with the 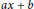$ax\,+\,b$ group, we show that the operator is of the form 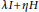$\lambda I+\eta H$, where $I$ and 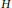$H$ are the identity operator and Hilbert transformation, respectively, and $\lambda ,\eta $ are complex numbers. In the related literature this result was proved by first invoking the boundedness result of the operator using some machinery. In our setting the boundedness is a consequence of the boundedness of the Hilbert transformation. The methodology that we use is the Gelfand–Naimark representation of the 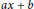$ax\,+\,b$ group. Furthermore, we prove a similar result on the unit circle. Although there does not exist a group like the 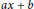$ax\,+\,b$ group on the unit circle, we construct a semigroup that plays the same symmetry role for the Hilbert transformations over the circle 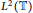${{L}^{2}}(\mathbb{T})$.

Keywords

30E2544A1542A50singular integralHilbert transformthe ax + b group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 70 - 84
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bell, S. R., The Cauchy transform, potential theory, and conformal mapping. Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1992.Google Scholar
[2] Folland, G. B., A Course in abstract harmonic analysis. Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1995.Google Scholar
[3] Garnett, J. B., Bounded analytic functions. Pure and Applied Mathematics, 96, Academic Press, New York-London, 1981.Google Scholar
[4] Gelfand, I. M. and Naimark, M. A., Unitary representations of the group of linear transformations ofthe straight line. C. R. (Doklady) Acad. Sei. URSS (N.S.) 55(1947), 567—570.Google Scholar
[5] Huang, J. F., Wang, Y., and Yang, L., Vakman's problem and the extension ofHilbert transform. Appl. Comput. Harmon. Anal. 34 (2013), no. 2, 308–316. http://dx.doi.Org/10.1016/j.acha.2012.08.009.Google Scholar
[6] Johnson, B. E., Continuity of linear Operators commuting with continuous linear Operators. Trans. Amer. Math. Soc. 128 (1967), 88–102. http://dx.doi.Org/10.2307/1994518.Google Scholar
[7] King, F. W., Hilbert transforms. Encyclopedia of Mathematics and its Applications, 125, Cambridge University Press, Cambridge, 2009.Google Scholar
[8] Knapp, A. W., Representation theory of semisimple groups. An overview based on examples. Reprint ofthe 1986 original, Princeton Landmarks in Mathematics, Princeton University Press, Princeton, NJ, 2001.Google Scholar
[9] Lu, J. K., Analytic boundary valueproblems. World Science, Singapore, 1993.Google Scholar
[10] Miklin, S. G. and Prodorf, S., Singular integral Operators. Springer-Verlag, Berlin, 1986. http://dx.doi.org/10.1007/978-3-642-61631-0.Google Scholar
[11] Qian, T., Characterization of boundary values of functions in Hardy Spaces with applications in signal analysis. J. Integral Equations Appl. 17 (2005), no. 2, 159–198. http://dx.doi.Org/10.1216/jiea/1181075323.Google Scholar
[12] Qian, T., Adaptive Fourier decomposition: a mathematical method through complex geometry, harmonic analysis and signal analysis. Chinese Science Press, 2015.Google Scholar
[13] Qian, T., Xu, Y. S., Yan, D. Y., Yan, L. X., and Yu, B., Fourier spectrurm characterization of Hardy Spaces and applications. Proc. Amer. Math. Soc, 137 (2009), 971–980. http://dx.doi.Org/10.1090/S0002-9939-08-09544-0.Google Scholar
[14] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[15] Vakman, D., On the analytic signal, the Teager-Kaiser energy algorithm, and other methods for defining amplitude and frequency. IEEE Trans. Signal Process. 44 (1996), no. 4, 791–797. http://dx.doi.org/10.1109/78.492532Google Scholar