In the first part of the paper, we use states on $C^{*}$-algebras in order to establish some equivalent statements to equality in the triangle inequality, as well as to the parallelogram identity for elements of a pre-Hilbert $C^{*}$-module. We also characterize the equality case in the triangle inequality for adjointable operators on a Hilbert $C^{*}$-module. Then we give certain necessary and sufficient conditions to the Pythagoras identity for two vectors in a pre-Hilbert $C^{*}$-module under the assumption that their inner product has a negative real part. We introduce the concept of Pythagoras orthogonality and discuss its properties. We describe this notion for Hilbert space operators in terms of the parallelogram law and some limit conditions. We present several examples in order to illustrate the relationship between the Birkhoff–James, Roberts, and Pythagoras orthogonalities, and the usual orthogonality in the framework of Hilbert $C^{*}$-modules.

In this paper, we obtain some characterizations of the (strong) Birkhoff–James orthogonality for elements of Hilbert 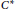${{C}^{*}}$-modules and certain elements of $\mathbb{B}\left( H \right)$. Moreover, we obtain a kind of Pythagorean relation for bounded linear operators. In addition, for 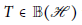$T\in \mathbb{B}(H)$ we prove that if the norm attaining set 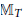${{\mathbb{M}}_{T}}$ is a unit sphere of some finite dimensional subspace 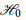${{H}_{0}}$ of 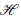$H$ and 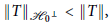$||T|{{|}_{{{H}_{0}}\bot }}\,<\,\,||T||$, then for every 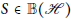$S\in \mathbb{B}(H)$, 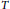$T$ is the strong Birkhoff–James orthogonal to $S$ if and only if there exists a unit vector 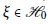$\xi \in {{H}_{0}}$ such that 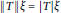$||T||\xi =\,|T|\xi $ and ${{S}^{*}}T\xi =0$. Finally, we introduce a new type of approximate orthogonality and investigate this notion in the setting of inner product 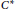${{C}^{*}}$-modules.

Extending the notion of parallelism we introduce the concept of approximate parallelism in normed spaces and then substantially restrict ourselves to the setting of Hilbert space operators endowed with the operator norm. We present several characterizations of the exact and approximate operator parallelism in the algebra $\mathbb{B}\left( H \right)$ of bounded linear operators acting on a Hilbert space $H$. Among other things, we investigate the relationship between the approximate parallelism and norm of inner derivations on $\mathbb{B}\left( H \right)$. We also characterize the parallel elements of a ${{C}^{*}}$-algebra by using states. Finally we utilize the linking algebra to give some equivalent assertions regarding parallel elements in a Hilbert ${{C}^{*}}$-module.