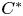1. Introduction
Let $S(\mathcal {A})$![]() be the set of all states of a given $C^{*}$
be the set of all states of a given $C^{*}$![]() -algebra $\mathcal {A}$
-algebra $\mathcal {A}$![]() . The numerical range of an element $a\in \mathcal {A}$
. The numerical range of an element $a\in \mathcal {A}$![]() is defined by
is defined by
If $a$![]() is a normal element of $\mathcal {A}$
is a normal element of $\mathcal {A}$![]() then there exists a state $\varphi$
then there exists a state $\varphi$![]() on $\mathcal {A}$
on $\mathcal {A}$![]() such that $|\varphi (a)|=\|a\|$
such that $|\varphi (a)|=\|a\|$![]() (cf. [Reference Murphy17, Theorem 3.3.6]). The set
(cf. [Reference Murphy17, Theorem 3.3.6]). The set
is nonempty and closed. This set is also convex if $a$![]() is positive.
is positive.
A (right) pre-Hilbert $C^{*}$![]() - module $\mathscr {E}$
- module $\mathscr {E}$![]() over a $C^{*}$
over a $C^{*}$![]() -algebra $\mathcal {A}$
-algebra $\mathcal {A}$![]() is a (complex) linear space which is also a right $\mathcal {A}$
is a (complex) linear space which is also a right $\mathcal {A}$![]() -module, having a compatible structure (i.e., $\lambda (xa)=(\lambda x)a=x(\lambda a),\ \lambda \in \mathbb {C},a\in \mathcal {A},x\in \mathscr {E}$
-module, having a compatible structure (i.e., $\lambda (xa)=(\lambda x)a=x(\lambda a),\ \lambda \in \mathbb {C},a\in \mathcal {A},x\in \mathscr {E}$![]() ), equipped with an $\mathcal {A}$
), equipped with an $\mathcal {A}$![]() -valued inner product on $\mathscr {E}$
-valued inner product on $\mathscr {E}$![]() , i.e., a sesquilinear map $\langle \cdot ,\cdot \rangle : \mathscr {E}\times \mathscr {E}\to \mathcal {A}$
, i.e., a sesquilinear map $\langle \cdot ,\cdot \rangle : \mathscr {E}\times \mathscr {E}\to \mathcal {A}$![]() with the properties:
with the properties:
(a) $\langle {x,x}\rangle \ge 0,\ x\in \mathscr {E}$
 ; $\langle {x,x}\rangle =0$
; $\langle {x,x}\rangle =0$ if and only if $x=0$
if and only if $x=0$ .
.(b) $\langle {x,y}\rangle ^{*}=\langle {y,x}\rangle ,\ x,y\in \mathscr {E}$
 .
.(c) $\langle {x,ya}\rangle =\langle {x,y}\rangle a ,\ x,y\in \mathscr {E},\ a\in \mathcal {A}$
 .
.
The formula
defines a norm on $\mathscr {E}$![]() (for $x\in \mathscr {E}$
(for $x\in \mathscr {E}$![]() , the notation $|x|:=\langle {x,x}\rangle ^{1/2}$
, the notation $|x|:=\langle {x,x}\rangle ^{1/2}$![]() will be used in the subsequent part of the paper). A pre-Hilbert $\mathcal {A}$
will be used in the subsequent part of the paper). A pre-Hilbert $\mathcal {A}$![]() -module which is complete with respect to this norm is called a Hilbert $C^{*}$
-module which is complete with respect to this norm is called a Hilbert $C^{*}$![]() -module over $\mathcal {A}$
-module over $\mathcal {A}$![]() , or a Hilbert $\mathcal {A}$
, or a Hilbert $\mathcal {A}$![]() -module. Every $C^{*}$
-module. Every $C^{*}$![]() -algebra $\mathcal {A}$
-algebra $\mathcal {A}$![]() can be regarded as a Hilbert module over itself, the inner product being defined as $\langle {a,b}\rangle :=a^{*}b,\ a,b\in \mathcal {A}$
can be regarded as a Hilbert module over itself, the inner product being defined as $\langle {a,b}\rangle :=a^{*}b,\ a,b\in \mathcal {A}$![]() .
.
Suppose that $\mathscr {E}$![]() and $\mathscr {F}$
and $\mathscr {F}$![]() are Hilbert $C^{*}$
are Hilbert $C^{*}$![]() -modules. Let $\mathcal {L}(\mathscr {E}, \mathscr {F})$
-modules. Let $\mathcal {L}(\mathscr {E}, \mathscr {F})$![]() be the set of all maps $T :\mathscr {E}\to \mathscr {F}$
be the set of all maps $T :\mathscr {E}\to \mathscr {F}$![]() for which there is an application $T^{*}:\mathscr {F}\to \mathscr {E}$
for which there is an application $T^{*}:\mathscr {F}\to \mathscr {E}$![]() such that
such that
An operator $T\in \mathcal {L}(\mathscr {E},\mathscr {F})$![]() , called adjointable, is $\mathcal {A}$
, called adjointable, is $\mathcal {A}$![]() -linear and bounded, while $T^{*}$
-linear and bounded, while $T^{*}$![]() (the adjoint of $T$
(the adjoint of $T$![]() ) is uniquely determined by (1). The map $T\mapsto T^{*}$
) is uniquely determined by (1). The map $T\mapsto T^{*}$![]() has the properties of an isometric involution. Moreover, $\mathcal {L}(\mathscr {E}):=\mathcal {L}(\mathscr {E},\mathscr {E})$
has the properties of an isometric involution. Moreover, $\mathcal {L}(\mathscr {E}):=\mathcal {L}(\mathscr {E},\mathscr {E})$![]() is a $C^{*}$
is a $C^{*}$![]() -algebra.
-algebra.
Thus, Hilbert $C^{*}$![]() -modules are generalization of Hilbert spaces by allowing inner products to take values in a $C^{*}$
-modules are generalization of Hilbert spaces by allowing inner products to take values in a $C^{*}$![]() -algebra rather than in the field of complex numbers. Unfortunately, certain basic properties of Hilbert spaces are not valid in general Hilbert $C^{*}$
-algebra rather than in the field of complex numbers. Unfortunately, certain basic properties of Hilbert spaces are not valid in general Hilbert $C^{*}$![]() -modules. For example, it is not true that any bounded linear operator on a Hilbert $C^{*}$
-modules. For example, it is not true that any bounded linear operator on a Hilbert $C^{*}$![]() -module is adjointable or any closed submodule is orthogonally complemented. Therefore, not only any investigation in the context of Hilbert $C^{*}$
-module is adjointable or any closed submodule is orthogonally complemented. Therefore, not only any investigation in the context of Hilbert $C^{*}$![]() -modules is non-trivial, but also it is an interesting question to ask under which conditions the results analogous to those for Hilbert spaces can still remain true for Hilbert $C^{*}$
-modules is non-trivial, but also it is an interesting question to ask under which conditions the results analogous to those for Hilbert spaces can still remain true for Hilbert $C^{*}$![]() -modules.
-modules.
It is known that the equality $\|x + y\|=\|x\| +\|y\|$![]() holds in a Hilbert space $\mathscr {H}$
holds in a Hilbert space $\mathscr {H}$![]() if and only if $x$
if and only if $x$![]() and $y$
and $y$![]() are linearly dependent by positive scalars. Being a starting point in our discussion on Pythagoras identities, one of our goals is to investigate the validity of this equality in the setting of Hilbert $C^{*}$
are linearly dependent by positive scalars. Being a starting point in our discussion on Pythagoras identities, one of our goals is to investigate the validity of this equality in the setting of Hilbert $C^{*}$![]() - modules. Maybe the first result in this direction is a characterization of Arambašić and Rajić [Reference Arambašić and Rajić2] which shows that, for two elements $x$
- modules. Maybe the first result in this direction is a characterization of Arambašić and Rajić [Reference Arambašić and Rajić2] which shows that, for two elements $x$![]() and $y$
and $y$![]() in a pre-Hilbert $\mathcal {A}$
in a pre-Hilbert $\mathcal {A}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() , $\|x + y\|=\|x\| +\|y\|$
, $\|x + y\|=\|x\| +\|y\|$![]() if and only if $\|x\|\|y\|\in V(\langle {x,y}\rangle )$
if and only if $\|x\|\|y\|\in V(\langle {x,y}\rangle )$![]() . The particular situations of Hilbert space operators or of elements in a $C^{*}$
. The particular situations of Hilbert space operators or of elements in a $C^{*}$![]() -algebra have been emphasized earlier by Barraa and Boumazgour [Reference Barraa and Boumazgour6], respectively by Nakamoto and Takahasi [Reference Nakamoto and Takahasi18]. We show, among others, that the following statements are equivalent: $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$
-algebra have been emphasized earlier by Barraa and Boumazgour [Reference Barraa and Boumazgour6], respectively by Nakamoto and Takahasi [Reference Nakamoto and Takahasi18]. We show, among others, that the following statements are equivalent: $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$![]() ; $\||x||y|\|=\|x\|\|y\|$
; $\||x||y|\|=\|x\|\|y\|$![]() ; $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$
; $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$![]() ; $\|x\|^{2}\|y\|^{2}\in V(|x|^{2}|y|^{2})$
; $\|x\|^{2}\|y\|^{2}\in V(|x|^{2}|y|^{2})$![]() ; $\|x\|^{2}+\|y\|^{2}\in V(|x|^{2}+|y|^{2})$
; $\|x\|^{2}+\|y\|^{2}\in V(|x|^{2}+|y|^{2})$![]() . We also discuss the ‘triangle equality’ for two adjointable operators $s$
. We also discuss the ‘triangle equality’ for two adjointable operators $s$![]() and $t$
and $t$![]() on $\mathscr {E}$
on $\mathscr {E}$![]() . By contrast with the earlier approach, our result relies on the states of $\mathcal {A}$
. By contrast with the earlier approach, our result relies on the states of $\mathcal {A}$![]() and not on the states of the $C^{*}$
and not on the states of the $C^{*}$![]() -algebra $\mathcal{L}(\mathscr {E})$
-algebra $\mathcal{L}(\mathscr {E})$![]() . More precisely, we prove that $\|s+t\|=\|s\|+\|t\|$
. More precisely, we prove that $\|s+t\|=\|s\|+\|t\|$![]() if and only if there exist sequences $(\varphi _n)_{n\ge 0}$
if and only if there exist sequences $(\varphi _n)_{n\ge 0}$![]() (of states on $\mathcal {A}$
(of states on $\mathcal {A}$![]() ) and $(x_n)_{n\ge 0}$
) and $(x_n)_{n\ge 0}$![]() (of elements in $\mathscr {E}$
(of elements in $\mathscr {E}$![]() ) such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$
) such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$![]() and $\varphi _n(\langle {sx_n,tx_n}\rangle )\xrightarrow {n\to \infty }\|s\|\|t\|$
and $\varphi _n(\langle {sx_n,tx_n}\rangle )\xrightarrow {n\to \infty }\|s\|\|t\|$![]() .
.
A norm $\|\cdot \|$![]() on a vector space $\mathscr {X}$
on a vector space $\mathscr {X}$![]() is induced by a scalar product if and only if the parallelogram identity $\|x+y\|^{2}+\|x-y\|^{2}=2(\|x\|^{2}+\|y\|^{2})$
is induced by a scalar product if and only if the parallelogram identity $\|x+y\|^{2}+\|x-y\|^{2}=2(\|x\|^{2}+\|y\|^{2})$![]() holds for every $x,y\in \mathscr {X}$
holds for every $x,y\in \mathscr {X}$![]() . This parallelogram identity is not valid in the general framework of Hilbert $C^{*}$
. This parallelogram identity is not valid in the general framework of Hilbert $C^{*}$![]() -modules. In our attempt to characterize this notion using the language of states, we show that any two of the following statements imply the third one: $x$
-modules. In our attempt to characterize this notion using the language of states, we show that any two of the following statements imply the third one: $x$![]() and $y$
and $y$![]() verify the parallelogram identity; $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$
verify the parallelogram identity; $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$![]() ; $S_{|x+y|^{2}}(\mathcal {A})\cap S_{|x-y|^{2}}(\mathcal {A})\ne \emptyset$
; $S_{|x+y|^{2}}(\mathcal {A})\cap S_{|x-y|^{2}}(\mathcal {A})\ne \emptyset$![]() .
.
Our next aim was to characterize an equality of the form $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$![]() (Pythagoras identity). This identity has been studied by many authors, in various contexts, starting with James [Reference James11]. We prove, under the assumption that the inner product $\langle {x,y}\rangle$
(Pythagoras identity). This identity has been studied by many authors, in various contexts, starting with James [Reference James11]. We prove, under the assumption that the inner product $\langle {x,y}\rangle$![]() has negative real part, that the following statements are equivalent: $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
has negative real part, that the following statements are equivalent: $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$![]() ; $\|x\|^{2}+\|y\|^{2}\in V(|x+y|^{2})$
; $\|x\|^{2}+\|y\|^{2}\in V(|x+y|^{2})$![]() ; there exists $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$
; there exists $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$![]() such that $\varphi (\Re (\langle {x,y}\rangle ))=0$
such that $\varphi (\Re (\langle {x,y}\rangle ))=0$![]() .
.
In the general context of (complex) normed linear spaces $\mathscr {X}$![]() , there were several attempts to extend the notion of orthogonality for two vectors $x$
, there were several attempts to extend the notion of orthogonality for two vectors $x$![]() and $y$
and $y$![]() . More exactly, $x$
. More exactly, $x$![]() and $y$
and $y$![]() are orthogonal in the Roberts sense (in notation, $x\perp _Ry$
are orthogonal in the Roberts sense (in notation, $x\perp _Ry$![]() ; cf. [Reference Roberts20, p. 56]) if $\|{x+\lambda y}\|=\|{x-\lambda y}\|,\ \lambda \in \mathbb {C}$
; cf. [Reference Roberts20, p. 56]) if $\|{x+\lambda y}\|=\|{x-\lambda y}\|,\ \lambda \in \mathbb {C}$![]() . The concept of Birkhoff–James orthogonality (in notation, $x\perp _By$
. The concept of Birkhoff–James orthogonality (in notation, $x\perp _By$![]() ), has been suggested by G. Birkhoff [Reference Birkhoff9] and R.C. James [Reference James12] as $\|{x+\lambda y}\|\ge \|{x}\|,\ \lambda \in \mathbb {C}$
), has been suggested by G. Birkhoff [Reference Birkhoff9] and R.C. James [Reference James12] as $\|{x+\lambda y}\|\ge \|{x}\|,\ \lambda \in \mathbb {C}$![]() . In the framework of pre-Hilbert $C^{*}$
. In the framework of pre-Hilbert $C^{*}$![]() -modules, these notions have been studied, for example, in [Reference Arambašić and Rajić3, Reference Arambašić and Rajić4, Reference Bhattacharyya and Grover8, Reference Moslehian and Zamani16].
-modules, these notions have been studied, for example, in [Reference Arambašić and Rajić3, Reference Arambašić and Rajić4, Reference Bhattacharyya and Grover8, Reference Moslehian and Zamani16].
The main part of this paper is devoted to the study of another concept of orthogonality, namely the Pythagoras orthogonality. A vector $x$![]() is said to be orthogonal in the Pythagoras sense to a vector $y$
is said to be orthogonal in the Pythagoras sense to a vector $y$![]() (in notation, $x\perp _P y$
(in notation, $x\perp _P y$![]() ) if
) if
If $x\perp _P y$![]() then, clearly, $x$
then, clearly, $x$![]() and $y$
and $y$![]() satisfy the parallelogram law, that is
satisfy the parallelogram law, that is
We start by presenting the main properties of Pythagoras orthogonality and discuss its relationship with the parallelogram law, Roberts orthogonality, Birkhoff–James orthogonality and inner product orthogonality. Pythagoras orthogonality implies both the parallelogram law and Birkhoff–James orthogonality. We show that, for two elements $x$![]() and $y$
and $y$![]() in $\mathscr {E}$
in $\mathscr {E}$![]() (a pre-Hilbert module over a unital $C^{*}$
(a pre-Hilbert module over a unital $C^{*}$![]() -algebra) such that $|y|^{2}$
-algebra) such that $|y|^{2}$![]() is a positive multiple of the identity, the converse is also true. We finally characterize the Pythagoras orthogonality for two operators $A$
is a positive multiple of the identity, the converse is also true. We finally characterize the Pythagoras orthogonality for two operators $A$![]() and $B$
and $B$![]() in $\mathcal {L}(\mathscr {H})$
in $\mathcal {L}(\mathscr {H})$![]() (regarded as a Hilbert module over itself) as follows. Under the assumptions that $\operatorname {rank}(A+\alpha _1 B)>1$
(regarded as a Hilbert module over itself) as follows. Under the assumptions that $\operatorname {rank}(A+\alpha _1 B)>1$![]() and $\Re (\alpha _2A^{*}B)\ge 0$
and $\Re (\alpha _2A^{*}B)\ge 0$![]() for certain $\alpha _1,\alpha _2\in \mathbb {C},\ \alpha _2\ne 0$
for certain $\alpha _1,\alpha _2\in \mathbb {C},\ \alpha _2\ne 0$![]() , $A$
, $A$![]() and $B$
and $B$![]() are orthogonal in the Pythagoras sense if and only if $A$
are orthogonal in the Pythagoras sense if and only if $A$![]() and $B$
and $B$![]() verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$
verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() such that $\|A\xi _n\|\xrightarrow {n\to \infty }\|A\|,\ \|B\xi _n\|\xrightarrow {n\to \infty }\|B\|$
such that $\|A\xi _n\|\xrightarrow {n\to \infty }\|A\|,\ \|B\xi _n\|\xrightarrow {n\to \infty }\|B\|$![]() and $\langle {A\xi _n,B\xi _n}\rangle \xrightarrow {n\to \infty }0$
and $\langle {A\xi _n,B\xi _n}\rangle \xrightarrow {n\to \infty }0$![]() if and only if $A$
if and only if $A$![]() and $B$
and $B$![]() verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$
verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() such that $\|(A+\lambda B)\xi _n\|^{2}\xrightarrow {n\to \infty }\|A\|^{2}+|\lambda |^{2}\|B\|^{2}$
such that $\|(A+\lambda B)\xi _n\|^{2}\xrightarrow {n\to \infty }\|A\|^{2}+|\lambda |^{2}\|B\|^{2}$![]() for every $\lambda \in \mathbb {C}$
for every $\lambda \in \mathbb {C}$![]() . Several examples are given for illustrative purposes.
. Several examples are given for illustrative purposes.
2. “Triangle equalities”
We start our work by the observation that the equality case in the triangle inequality for two elements $x$![]() and $y$
and $y$![]() in a normed linear space $\mathscr {X}$
in a normed linear space $\mathscr {X}$![]() is preserved for their positive multiples $\alpha x\ (\alpha \ge 0)$
is preserved for their positive multiples $\alpha x\ (\alpha \ge 0)$![]() and $\beta y\ (\beta \ge 0)$
and $\beta y\ (\beta \ge 0)$![]() .
.
Lemma 2.1 Abramovich et al. [Reference Abramovich, Aliprantis and Burkinshaw1, Lemma 2.1]
Let $x$![]() and $y$
and $y$![]() be two vectors in a normed linear space $\mathscr {X}$
be two vectors in a normed linear space $\mathscr {X}$![]() such that $\|x+y\|=\|x\|+\|y\|$
such that $\|x+y\|=\|x\|+\|y\|$![]() . Then $\|\alpha x+\beta y\| =\alpha \|x\|+\beta \|y\|$
. Then $\|\alpha x+\beta y\| =\alpha \|x\|+\beta \|y\|$![]() for every $\alpha ,\beta \ge 0$
for every $\alpha ,\beta \ge 0$![]() .
.
An equality of the form $\|\alpha x+\beta y\|=|\alpha |\|x\|+|\beta |\|y\|$![]() ($\alpha ,\beta \in \mathbb {C},\ \alpha ,\beta \ne 0$
($\alpha ,\beta \in \mathbb {C},\ \alpha ,\beta \ne 0$![]() ) can be reformulated for scalars $\alpha ,\beta$
) can be reformulated for scalars $\alpha ,\beta$![]() belonging to the unit circle $\mathbb {T}$
belonging to the unit circle $\mathbb {T}$![]() . More precisely, the following holds.
. More precisely, the following holds.
Proposition 2.2 Let $x$![]() and $y$
and $y$![]() be two vectors of a normed linear space $\mathscr {X}$
be two vectors of a normed linear space $\mathscr {X}$![]() . The following statements are equivalent:
. The following statements are equivalent:
(i) $\|\alpha x+\beta y\|=|\alpha |\|x\|+|\beta |\|y\|$
 for some nonzero scalars $\alpha ,\beta \in \mathbb {C}$
for some nonzero scalars $\alpha ,\beta \in \mathbb {C}$ .
.(ii) $\|\alpha x+\beta y\|=\| x\|+\|y\|$
 for some $\alpha ,\beta \in \mathbb {T}$
for some $\alpha ,\beta \in \mathbb {T}$ .
.
Proof. We only have to prove the implication $(i)\Rightarrow (ii)$![]() , the other one is obvious. Let $x'=\alpha x$
, the other one is obvious. Let $x'=\alpha x$![]() and $y'=\beta y$
and $y'=\beta y$![]() . Then $(i)$
. Then $(i)$![]() takes the form $\|x'+y'\|=\|x'\|+\|y'\|$
takes the form $\|x'+y'\|=\|x'\|+\|y'\|$![]() so, by Lemma 2.1, $\|{1}/{|\alpha |}x'+({1}/{|\beta |})y'\|={1}/{|\alpha |}\|x'\|+{1}/{|\beta |}\|y'\|$
so, by Lemma 2.1, $\|{1}/{|\alpha |}x'+({1}/{|\beta |})y'\|={1}/{|\alpha |}\|x'\|+{1}/{|\beta |}\|y'\|$![]() . In other words,
. In other words,
The following result, characterizing the equality case in the triangle inequality for two elements of a pre-Hilbert $\mathcal {A}$![]() -module has been formulated in [Reference Popovici19, Proposition 3] using a representation of $\mathcal {A}$
-module has been formulated in [Reference Popovici19, Proposition 3] using a representation of $\mathcal {A}$![]() on a Hilbert space. It will be presented here using the terminology of states. We would also like to mention that the equivalence $(i)\Leftrightarrow (iii)$
on a Hilbert space. It will be presented here using the terminology of states. We would also like to mention that the equivalence $(i)\Leftrightarrow (iii)$![]() has been obtained in [Reference Arambašić and Rajić2, Theorem 2.1].
has been obtained in [Reference Arambašić and Rajić2, Theorem 2.1].
Proposition 2.3 Popovici [Reference Popovici19, Proposition 3]
Let $x,y$![]() be two elements in a pre-Hilbert module over a $C^{*}$
be two elements in a pre-Hilbert module over a $C^{*}$![]() -algebra $\mathcal {A}$
-algebra $\mathcal {A}$![]() . The following statements are equivalent:
. The following statements are equivalent:
(i) $\|x+y\|=\|x\|+\|y\|$
 .
.(ii) $(\|x\|+\|y\|)^{2}\in V(|x+y|^{2})$
 .
.(iii) $\|x\|\|y\|\in V(\langle {x,y}\rangle )$
 .
.
If $\varphi$![]() is a given state on $\mathcal {A},$
is a given state on $\mathcal {A},$![]() then $\varphi (|x+y|^{2})=(\|x\|+\|y\|)^{2}$
then $\varphi (|x+y|^{2})=(\|x\|+\|y\|)^{2}$![]() if and only if $\varphi (\langle {x,y}\rangle )=\|x\|\|y\|$
if and only if $\varphi (\langle {x,y}\rangle )=\|x\|\|y\|$![]() . In this case, $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$
. In this case, $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$![]() and $\varphi (\langle {x,y}\rangle ^{*}\langle {x,y}\rangle )=\|x\|^{2}\|y\|^{2}$
and $\varphi (\langle {x,y}\rangle ^{*}\langle {x,y}\rangle )=\|x\|^{2}\|y\|^{2}$![]() .
.
We now describe a triangle ‘equality’ in the context of pre-Hilbert $C^{*}$![]() -modules.
-modules.
Proposition 2.4 Let $x$![]() and $y$
and $y$![]() be two elements of a pre-Hilbert $\mathcal {A}$
be two elements of a pre-Hilbert $\mathcal {A}$![]() -module. The following statements are equivalent:
-module. The following statements are equivalent:
(i) $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$
 .
.(ii) $\||x||y|\|=\|x\|\|y\|$
 .
.(iii) $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$
 .
.(iv) $\|x\|^{2}\|y\|^{2}\in V(|x|^{2}|y|^{2})$
 .
.(v) $\|x\|^{2}+\|y\|^{2}\in V(|x|^{2}+|y|^{2})$
 .
.
Proof. We only prove $(v)\Rightarrow (i)$![]() , the rest can be concluded from [Reference Kittaneh13, Proposition 3.3], [Reference Arambašić and Rajić2, Theorem 2.1], and [Reference Nakamoto and Takahasi18, Theorem 1]). To this end, it is enough to show that if $a$
, the rest can be concluded from [Reference Kittaneh13, Proposition 3.3], [Reference Arambašić and Rajić2, Theorem 2.1], and [Reference Nakamoto and Takahasi18, Theorem 1]). To this end, it is enough to show that if $a$![]() and $b$
and $b$![]() are two positive elements of a $C^{*}$
are two positive elements of a $C^{*}$![]() -algebra $\mathcal {A}$
-algebra $\mathcal {A}$![]() , and $\|a\|+\|b\|\in V(a+b)$
, and $\|a\|+\|b\|\in V(a+b)$![]() , then $\|a+b\|=\|a\|+\|b\|$
, then $\|a+b\|=\|a\|+\|b\|$![]() :
:
Let $\varphi \in S(\mathcal {A})$![]() be such that $\varphi (a+b)=\|a\|+\|b\|$
be such that $\varphi (a+b)=\|a\|+\|b\|$![]() . Then
. Then
We deduce immediately that $\|a+b\|=\|a\|+\|b\|$![]() , as required.
, as required.
We need the next result, which is an immediate consequence of the above proposition.
Corollary 2.5 Let $a$![]() and $b$
and $b$![]() be two elements of $\mathcal {A}$
be two elements of $\mathcal {A}$![]() . The following statements are equivalent:
. The following statements are equivalent:
(i) $\|a^{*}a+b^{*}b\|=\|a\|^{2}+\|b\|^{2}$
 .
.(ii) $\|ab^{*}\|=\|a\|\|b\|$
 .
.
Corollary 2.6 Let $x$![]() and $y$
and $y$![]() be two elements of a pre-Hilbert $\mathcal {A}$
be two elements of a pre-Hilbert $\mathcal {A}$![]() -module. Then any two of the following statements imply the third one:
-module. Then any two of the following statements imply the third one:
(i) $x$
 and $y$
and $y$ verify the parallelogram law:
\[ \|x+y\|^{2}+\|x-y\|^{2}=2(\|x\|^{2}+\|y\|^{2}). \]
verify the parallelogram law:
\[ \|x+y\|^{2}+\|x-y\|^{2}=2(\|x\|^{2}+\|y\|^{2}). \]
(ii) $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$
 .
.(iii) $S_{|x+y|^{2}}(\mathcal {A})\cap S_{|x-y|^{2}}(\mathcal {A})\ne \emptyset$
 .
.
Proof. By Proposition 2.4, condition $(ii)$![]() is equivalent to $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$
is equivalent to $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$![]() . Similarly, condition $(iii)$
. Similarly, condition $(iii)$![]() can be replaced by:
can be replaced by:
The conclusion then follows easily.
Our next aim is to describe the equality case in the triangle inequality for two adjointable operators in a Hilbert $C^{*}$![]() -module.
-module.
Theorem 2.7 Let $\mathscr {E}$![]() be a Hilbert module over the $C^{*}$
be a Hilbert module over the $C^{*}$![]() -algebra $\mathcal {A},$
-algebra $\mathcal {A},$![]() and let $s,t\in \mathcal {L}(\mathscr {E})$
and let $s,t\in \mathcal {L}(\mathscr {E})$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(i) $\|s+t\|=\|s\|+\|t\|$
 .
.(ii) There exist sequences $(\varphi _n)_{n\ge 0}$
 (of states on $\mathcal {A}$
(of states on $\mathcal {A}$ ) and $(x_n)_{n\ge 0}$
) and $(x_n)_{n\ge 0}$ (of elements in $\mathscr {E}$
(of elements in $\mathscr {E}$ ) such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$
) such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$ and
\[ \varphi_n(\langle{sx_n,tx_n}\rangle)\xrightarrow{n\to\infty}\|s\|\|t\|. \]
and
\[ \varphi_n(\langle{sx_n,tx_n}\rangle)\xrightarrow{n\to\infty}\|s\|\|t\|. \]
(iii) There exist sequences $(\varphi _n)_{n\ge 0}$
 (of states on $\mathcal {A}$
(of states on $\mathcal {A}$ ) and $(x_n)_{n\ge 0}$
) and $(x_n)_{n\ge 0}$ (of elements in $\mathscr {E}$
(of elements in $\mathscr {E}$ ) such that $\varphi _n(|x_n|^{2})\le 1,\ n\ge 0$
) such that $\varphi _n(|x_n|^{2})\le 1,\ n\ge 0$ and
\[ \varphi_n(\langle{sx_n,tx_n}\rangle)\xrightarrow{n\to\infty}\|s\|\|t\|. \]
and
\[ \varphi_n(\langle{sx_n,tx_n}\rangle)\xrightarrow{n\to\infty}\|s\|\|t\|. \]
Proof. It has been indicated in [Reference Lance14, p. 37] that, for any given state $\varphi$![]() of $\mathcal {A}$
of $\mathcal {A}$![]() and $x\in \mathscr {E}$
and $x\in \mathscr {E}$![]() with $\varphi (|x|^{2})=1$
with $\varphi (|x|^{2})=1$![]() , the map $s\mapsto \varphi (\langle {x,sx}\rangle )$
, the map $s\mapsto \varphi (\langle {x,sx}\rangle )$![]() is a state of $\mathcal {L}(\mathscr {E})$
is a state of $\mathcal {L}(\mathscr {E})$![]() . In addition, for any adjointable operator $s$
. In addition, for any adjointable operator $s$![]() on $\mathscr {E}$
on $\mathscr {E}$![]() ,
,
$(i)\Rightarrow (ii)$![]() . Let us consider, in view of (2), a sequence $(\varphi _n)_{n\ge 0}$
. Let us consider, in view of (2), a sequence $(\varphi _n)_{n\ge 0}$![]() of states on $\mathcal {A}$
of states on $\mathcal {A}$![]() and a sequence $(x_n)_{n\ge 0}$
and a sequence $(x_n)_{n\ge 0}$![]() of elements in $\mathscr {E}$
of elements in $\mathscr {E}$![]() such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$
such that $\varphi _n(|x_n|^{2})=1,\ n\ge 0$![]() and
and
We note that, for any $n\ge 0$![]() ,
,

We pass to limit (as $n\to \infty$![]() ) to deduce, by $(i)$
) to deduce, by $(i)$![]() , that
, that
which proves $(ii)$![]() .
.
The implication $(ii)\Rightarrow (iii)$![]() is obvious.
is obvious.
$(iii)\Rightarrow (i)$![]() . Let $(\varphi _n)_{n\ge 0}$
. Let $(\varphi _n)_{n\ge 0}$![]() , and let $(x_n)_{n\ge 0}$
, and let $(x_n)_{n\ge 0}$![]() be sequences as in $(iii)$
be sequences as in $(iii)$![]() . By passing to limit (as $n\to \infty$
. By passing to limit (as $n\to \infty$![]() ) in the inequalities
) in the inequalities
we obtain that
Hence,
Letting again $n\to \infty$![]() in the inequalities $\varphi _n(|(s+t)x_n|^{2})\le \|s+t\|^{2}\le (\|s\|+\|t\|)^{2},\ n\ge 0$
in the inequalities $\varphi _n(|(s+t)x_n|^{2})\le \|s+t\|^{2}\le (\|s\|+\|t\|)^{2},\ n\ge 0$![]() we finally get the triangle ‘equality’ in $(i)$
we finally get the triangle ‘equality’ in $(i)$![]() .
.
3. Pythagoras identities
We characterize the Pythagoras identity for two vectors in a pre-Hilbert $C^{*}$![]() -modules under the assumption that their inner product has a negative real part.
-modules under the assumption that their inner product has a negative real part.
Proposition 3.1 Let $x$![]() and $y$
and $y$![]() be two elements in a pre-Hilbert $C^{*}$
be two elements in a pre-Hilbert $C^{*}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() such that $\Re (\langle {x,y}\rangle )\le 0$
such that $\Re (\langle {x,y}\rangle )\le 0$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(i) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}.$

(ii) $\||x|^{2}+2\Re (\langle {x,y}\rangle )+|y|^{2}\|=\||x|^{2}+|y|^{2}\|$
 and $\||x||y|\|=\|x\|\|y\|.$
and $\||x||y|\|=\|x\|\|y\|.$
Proof. Let us firstly note that
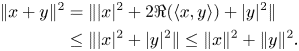
If $(i)$![]() holds true, then the inequalities in (3) become equalities. Also, by [Reference Kittaneh13, Proposition 3.3], the triangle equality $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$
holds true, then the inequalities in (3) become equalities. Also, by [Reference Kittaneh13, Proposition 3.3], the triangle equality $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$![]() can be written in the form $\||x||y|\|=\|x\|\|y\|$
can be written in the form $\||x||y|\|=\|x\|\|y\|$![]() , which is exactly the last condition of $(ii)$
, which is exactly the last condition of $(ii)$![]() . The converse follows the same path.
. The converse follows the same path.
Theorem 3.2 Let $x$![]() and $y$
and $y$![]() be two elements in a pre-Hilbert $C^{*}$
be two elements in a pre-Hilbert $C^{*}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() such that $\Re (\langle {x,y}\rangle )\le 0$
such that $\Re (\langle {x,y}\rangle )\le 0$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(i) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
 .
.(ii) $\|x\|^{2}+\|y\|^{2}\in V(|x+y|^{2})$
 .
.(iii) There exists $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$
 such that $\varphi (\Re (\langle {x,y}\rangle ))=0$
such that $\varphi (\Re (\langle {x,y}\rangle ))=0$ .
.
Proof. The implication $(i)\Rightarrow (ii)$![]() follows by [Reference Murphy17, Theorem 3.3.6].
follows by [Reference Murphy17, Theorem 3.3.6].
$(ii)\Rightarrow (i)$![]() . Conversely, if $\varphi$
. Conversely, if $\varphi$![]() is a state on $\mathcal {A}$
is a state on $\mathcal {A}$![]() as in $(ii)$
as in $(ii)$![]() , then, by (3),
, then, by (3),
Consequently, $(i)$![]() holds true.
holds true.
$(iii)\Rightarrow (ii)$![]() . Let $\varphi$
. Let $\varphi$![]() be a state on $\mathcal {A}$
be a state on $\mathcal {A}$![]() such that
such that
Then
$(ii)\Rightarrow (iii)$![]() . Conversely, let $\varphi \in S(\mathcal {A})$
. Conversely, let $\varphi \in S(\mathcal {A})$![]() be a state which satisfies condition $(ii)$
be a state which satisfies condition $(ii)$![]() . Then
. Then
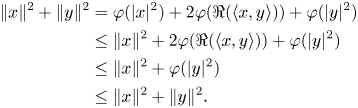
Thus, $\varphi (|x|^{2})=\|x\|^{2}$![]() , $\varphi (|y|^{2})=\|y\|^{2}$
, $\varphi (|y|^{2})=\|y\|^{2}$![]() and $\varphi (\Re (\langle {x,y}\rangle ))=0$
and $\varphi (\Re (\langle {x,y}\rangle ))=0$![]() . The statement $(iii)$
. The statement $(iii)$![]() is proved.
is proved.
Corollary 3.3 Let $x$![]() and $y$
and $y$![]() be two elements in a pre-Hilbert $C^{*}$
be two elements in a pre-Hilbert $C^{*}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() such that $\Re (\langle {x,y}\rangle )\le 0$
such that $\Re (\langle {x,y}\rangle )\le 0$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(i) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}.$

(ii) $\|\alpha x+\beta y\|^{2}=|\alpha |^{2}\|x\|^{2}+|\beta |^{2}\|y\|^{2}$
 for certain (equivalently, for every) $\alpha ,\beta \in \mathbb {C}$
for certain (equivalently, for every) $\alpha ,\beta \in \mathbb {C}$ with $\bar \alpha \beta >0$
with $\bar \alpha \beta >0$ .
.
Remark 3.4 If $\Re (\langle {x,y}\rangle )\le 0$![]() , then, by the Pythagoras identity $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
, then, by the Pythagoras identity $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$![]() , one can also obtain the following inequality:
, one can also obtain the following inequality:
for every complex numbers $\alpha ,\beta$![]() such that $\bar \alpha \beta$
such that $\bar \alpha \beta$![]() is real.
is real.
Indeed, if $\varphi$![]() is a state on $\mathcal {A}$
is a state on $\mathcal {A}$![]() satisfying condition $(iii)$
satisfying condition $(iii)$![]() of Theorem 3.2, then, for every $\alpha ,\beta \in \mathbb {C}$
of Theorem 3.2, then, for every $\alpha ,\beta \in \mathbb {C}$![]() with $\bar \alpha \beta \in \mathbb {R}$
with $\bar \alpha \beta \in \mathbb {R}$![]() , it holds
, it holds

Under the stronger assumption $\Re (\langle {x,y}\rangle )=0$![]() , the Pythagoras identities associated with the pairs $(x,y)$
, the Pythagoras identities associated with the pairs $(x,y)$![]() and, respectively, $(\alpha x,\beta y)$
and, respectively, $(\alpha x,\beta y)$![]() (for $\bar {\alpha }\beta \in \mathbb {R}^{*}$
(for $\bar {\alpha }\beta \in \mathbb {R}^{*}$![]() ) are actually equivalent.
) are actually equivalent.
Corollary 3.5 Let $x$![]() and $y$
and $y$![]() be two elements in a pre-Hilbert $C^{*}$
be two elements in a pre-Hilbert $C^{*}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() such that $\Re (\langle {x,y}\rangle )=0$
such that $\Re (\langle {x,y}\rangle )=0$![]() . The following statements are equivalent:
. The following statements are equivalent:
(i) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
 .
.(ii) $\|\alpha x+\beta y\|^{2}=|\alpha |^{2}\|x\|^{2}+|\beta |^{2}\|y\|^{2}$
 for certain (equivalently, for every) non-null complex numbers $\alpha$
for certain (equivalently, for every) non-null complex numbers $\alpha$ and $\beta$
and $\beta$ with $\bar \alpha \beta \in \mathbb {R}$
with $\bar \alpha \beta \in \mathbb {R}$ .
.(iii) $\||x||y|\|=\|x\|\|y\|$
 .
.(iv) $S_{|x+y|^{2}}(\mathcal {A})=S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$
 .
.
Proof. Under the assumption $\Re (\langle {x,y}\rangle )=0$![]() , condition $(i)$
, condition $(i)$![]() takes the form $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$
takes the form $\||x|^{2}+|y|^{2}\|=\|x\|^{2}+\|y\|^{2}$![]() . The equivalences between $(i),\ (ii),$
. The equivalences between $(i),\ (ii),$![]() and $(iii)$
and $(iii)$![]() are deduced from Proposition 2.4. By the same result, the statements are also equivalent to $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$
are deduced from Proposition 2.4. By the same result, the statements are also equivalent to $S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})\ne \emptyset$![]() . So $(iv)$
. So $(iv)$![]() implies $(i)$
implies $(i)$![]() . Finally, if $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
. Finally, if $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$![]() (condition $(i)$
(condition $(i)$![]() holds true), then, for any $\varphi \in S_{|x+y|^{2}}(\mathcal {A})$
holds true), then, for any $\varphi \in S_{|x+y|^{2}}(\mathcal {A})$![]() ,
,
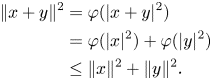
Hence, $\varphi \in S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$![]() . In other words, $S_{|x+y|^{2}}(\mathcal {A})\subseteq S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$
. In other words, $S_{|x+y|^{2}}(\mathcal {A})\subseteq S_{|x|^{2}}(\mathcal {A})\cap S_{|y|^{2}}(\mathcal {A})$![]() . The converse inclusion is obvious, so the statement $(iv)$
. The converse inclusion is obvious, so the statement $(iv)$![]() is verified.
is verified.
Corollary 3.6 Let $x$![]() and $y$
and $y$![]() be two elements in a pre-Hilbert $C^{*}$
be two elements in a pre-Hilbert $C^{*}$![]() -module $\mathscr {E}$
-module $\mathscr {E}$![]() such that $\langle {x,y}\rangle =0$
such that $\langle {x,y}\rangle =0$![]() . The following statements are equivalent:
. The following statements are equivalent:
(i) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}$
 .
.(ii) $\|\alpha x+\beta y\|^{2}=|\alpha |^{2}\|x\|^{2}+|\beta |^{2}\|y\|^{2}$
 for certain (equivalently, for every) nonzero complex numbers $\alpha$
for certain (equivalently, for every) nonzero complex numbers $\alpha$ and $\beta$
and $\beta$ .
.
4. Pythagoras orthogonality
It is our aim in this section to investigate the Pythagoras orthogonality in the context of Hilbert $C^{*}$![]() -modules. We list some properties of this notion, as follows:
-modules. We list some properties of this notion, as follows:
(a) If $x$
 and $y$
and $y$ are linearly dependent, then $x\perp _P y$
are linearly dependent, then $x\perp _P y$ if and only if $x=0$
if and only if $x=0$ or $y=0$
or $y=0$ . Due to this simple remark one may suppose, when trying to describe the concept of Pythagoras orthogonality, that the two vectors $x$
. Due to this simple remark one may suppose, when trying to describe the concept of Pythagoras orthogonality, that the two vectors $x$ and $y$
and $y$ are linearly independent. If not stated otherwise, we will make this assumption for the rest of the paper.
are linearly independent. If not stated otherwise, we will make this assumption for the rest of the paper.(b) In inner product spaces, $x\perp _P y$
 if and only if $\langle {x,y}\rangle =0$
if and only if $\langle {x,y}\rangle =0$ .
.(c) In pre-Hilbert $C^{*}$
 -modules, if $\langle {x,y}\rangle =0$
-modules, if $\langle {x,y}\rangle =0$ , then $x\perp _P y$
, then $x\perp _P y$ if and only if $\|x+\alpha y\|^{2}=\|x\|^{2}+|\alpha |^{2}\|y\|^{2}$
if and only if $\|x+\alpha y\|^{2}=\|x\|^{2}+|\alpha |^{2}\|y\|^{2}$ for a certain non-null $\alpha \in \mathbb {C}$
for a certain non-null $\alpha \in \mathbb {C}$ if and only if $\||x||y|\|=\|x\|\|y\|$
if and only if $\||x||y|\|=\|x\|\|y\|$ (see Corollaries 3.5 and 3.6).
(see Corollaries 3.5 and 3.6).(d) In normed $*$
 -algebras, $x\perp _P y$
-algebras, $x\perp _P y$ if and only if $x^{*}\perp _P y^{*}$
if and only if $x^{*}\perp _P y^{*}$ .
.(e) $x\perp _P x$
 if and only if $x=0$
if and only if $x=0$ (nondegenerate).
(nondegenerate).(f) $x\perp _P y$
 if and only if $y\perp _P x$
if and only if $y\perp _P x$ (symmetric).
(symmetric).(g) If $x\perp _P y$
 , then $(\alpha x)\perp _P(\beta y),\ \alpha ,\beta \in \mathbb {C}$
, then $(\alpha x)\perp _P(\beta y),\ \alpha ,\beta \in \mathbb {C}$ (homogeneous).
(homogeneous).(h) If $x\perp _P y$
 , then $x\perp _R y$
, then $x\perp _R y$ , $x\perp _B y$
, $x\perp _B y$ and $y\perp _B x$
and $y\perp _B x$ .
.(i) If $x\perp _P y$
 , then $x$
, then $x$ and $y$
and $y$ satisfy the parallelogram law.
satisfy the parallelogram law.(j) If $x\perp _R y$
 , then $x\perp _P y$
, then $x\perp _P y$ if and only if $x$
if and only if $x$ and $y$
and $y$ satisfy the parallelogram law.
satisfy the parallelogram law.
We describe, in a few examples, for elements $x,y$![]() in a pre-Hilbert $C^{*}$
in a pre-Hilbert $C^{*}$![]() -module, the relationship between the Birkhoff–James, Roberts and Pythagoras orthogonality, the parallelogram law and the equality $\langle {x,y}\rangle =0$
-module, the relationship between the Birkhoff–James, Roberts and Pythagoras orthogonality, the parallelogram law and the equality $\langle {x,y}\rangle =0$![]() .
.
Example 4.1 Let us consider the $C^{*}$![]() -algebra $\mathcal {L}(\mathscr {H})$
-algebra $\mathcal {L}(\mathscr {H})$![]() of bounded linear operators on a separable Hilbert space $\mathscr {H}$
of bounded linear operators on a separable Hilbert space $\mathscr {H}$![]() ($\mathcal {L}(\mathscr {H}$
($\mathcal {L}(\mathscr {H}$![]() ) is regarded as a Hilbert module over itself). For a given orthonormal basis $(e_n)_{n\ge 1}$
) is regarded as a Hilbert module over itself). For a given orthonormal basis $(e_n)_{n\ge 1}$![]() in $\mathscr {H}$
in $\mathscr {H}$![]() , we define $A,B\in \mathcal {L}(\mathscr {H})$
, we define $A,B\in \mathcal {L}(\mathscr {H})$![]() by
by
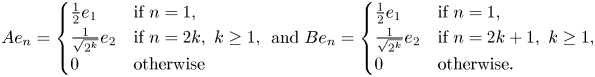
Then $\|A\|=\|B\|=1$![]() and, for any $\lambda \in \mathbb {C}$
and, for any $\lambda \in \mathbb {C}$![]() , we have
, we have
Hence, $A$![]() and $B$
and $B$![]() are orthogonal in the Pythagoras sense. Moreover, since $e_1\in \operatorname {ran} A\cap \operatorname {ran} B$
are orthogonal in the Pythagoras sense. Moreover, since $e_1\in \operatorname {ran} A\cap \operatorname {ran} B$![]() , $\langle {A,B}\rangle \neq 0$
, $\langle {A,B}\rangle \neq 0$![]() ($\operatorname {ran} A$
($\operatorname {ran} A$![]() denotes the range of $A$
denotes the range of $A$![]() ).
).
Example 4.2 Suppose that $\mathcal {A}$![]() is the $C^{*}$
is the $C^{*}$![]() -algebra $\mathcal {C}[0,1]$
-algebra $\mathcal {C}[0,1]$![]() of all complex valued continuous functions on the closed interval $[0,1]$
of all complex valued continuous functions on the closed interval $[0,1]$![]() (considered as a Hilbert $C^{*}$
(considered as a Hilbert $C^{*}$![]() -module over itself). Let $f,g\in \mathcal {A}$
-module over itself). Let $f,g\in \mathcal {A}$![]() be defined by
be defined by
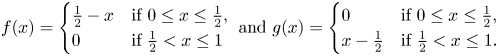
Then $\|f\|=\|g\|=\tfrac {1}{2}$![]() and, for $\lambda \in \mathbb {C}$
and, for $\lambda \in \mathbb {C}$![]() ,
,
It follows that $f\perp _B g,\ g\perp _B f$![]() and $f\perp _R g$
and $f\perp _R g$![]() . Although $\langle {f,g}\rangle =0$
. Although $\langle {f,g}\rangle =0$![]() , $f$
, $f$![]() and $g$
and $g$![]() are not orthogonal in the Pythagoras sense, since $\|f+\lambda g\|^{2}=\|f\|^{2}+|\lambda |^{2}\|g\|^{2}$
are not orthogonal in the Pythagoras sense, since $\|f+\lambda g\|^{2}=\|f\|^{2}+|\lambda |^{2}\|g\|^{2}$![]() if and only if $\lambda =0$
if and only if $\lambda =0$![]() . Equivalently, as $f\perp _R g$
. Equivalently, as $f\perp _R g$![]() , $f$
, $f$![]() and $g$
and $g$![]() do not satisfy the parallelogram law, either.
do not satisfy the parallelogram law, either.
Example 4.3 Let $S$![]() and $T$
and $T$![]() be bounded linear operators on $\mathscr {H}$
be bounded linear operators on $\mathscr {H}$![]() . If
. If
are elements of the $C^{*}$![]() -algebra $\mathcal {A}=\mathcal {L}(\mathscr {H}\oplus \mathscr {H})$
-algebra $\mathcal {A}=\mathcal {L}(\mathscr {H}\oplus \mathscr {H})$![]() , then $\|A\|=\|S\|$
, then $\|A\|=\|S\|$![]() , $\|B\|=\|T\|$
, $\|B\|=\|T\|$![]() and
and
One can immediately verify that $A\perp _B B,\ B\perp _B A$![]() and $A\perp _R B$
and $A\perp _R B$![]() . Also, by Corollary 2.5, $A$
. Also, by Corollary 2.5, $A$![]() and $B$
and $B$![]() are orthogonal in the Pythagoras sense if and only if $\|S^{*}T\|=\|S\|\|T\|$
are orthogonal in the Pythagoras sense if and only if $\|S^{*}T\|=\|S\|\|T\|$![]() . In particular, this orthogonality condition is satisfied, for example, when $S$
. In particular, this orthogonality condition is satisfied, for example, when $S$![]() is a scalar multiple of a coisometric operator or of an orthogonal projection $P$
is a scalar multiple of a coisometric operator or of an orthogonal projection $P$![]() with $\operatorname {ran}(P)\supseteq \operatorname {ran}(T)$
with $\operatorname {ran}(P)\supseteq \operatorname {ran}(T)$![]() .
.
In addition, one can immediately verify that, $A$![]() and $B$
and $B$![]() satisfy the parallelogram law if and only if they are orthogonal in the Pythagoras sense. On the other hand, $\langle {A,B}\rangle =A^{*}B=0$
satisfy the parallelogram law if and only if they are orthogonal in the Pythagoras sense. On the other hand, $\langle {A,B}\rangle =A^{*}B=0$![]() if and only if $\operatorname {ran} S\perp \operatorname {ran} T$
if and only if $\operatorname {ran} S\perp \operatorname {ran} T$![]() .
.
Example 4.4 For given $X\in \mathcal {L}(\mathscr {H})\setminus \{0\}$![]() and complex numbers $a,b,c,d$
and complex numbers $a,b,c,d$![]() we define (on the Hilbert space $\mathscr {H}\oplus \mathscr {H}$
we define (on the Hilbert space $\mathscr {H}\oplus \mathscr {H}$![]() ) the matrix operator
) the matrix operator
Its norm has been computed by Feldman, Krupnik, and Markus in [Reference Feldman, Krupnik and Markus10, Lemma 1.6] as
where $r=|a|^{2}+|d|^{2}+(|b|^{2}+|c|^{2})\|X\|^{2}$![]() and $s=2|ad-bc\|X\||$
and $s=2|ad-bc\|X\||$![]() .
.
Let $A=M_X(a,0,0,d)$![]() and $B=M_X(0,b,c,0)$
and $B=M_X(0,b,c,0)$![]() . After direct calculations, one may check that, regardless of the values of $a,b,c$
. After direct calculations, one may check that, regardless of the values of $a,b,c$![]() and $d$
and $d$![]() , $A\perp _B B$
, $A\perp _B B$![]() and $A\perp _R B$
and $A\perp _R B$![]() . On the other hand, $B\perp _B A$
. On the other hand, $B\perp _B A$![]() if and only if $bc=0$
if and only if $bc=0$![]() . We can also verify that the following conditions are equivalent:
. We can also verify that the following conditions are equivalent:
(i) $A$
 and $B$
and $B$ are orthogonal in the Pythagoras sense;
are orthogonal in the Pythagoras sense;(ii) $A$
 and $B$
and $B$ satisfy the parallelogram law;
satisfy the parallelogram law;(iii) $ad=bc=0$
 .
.
Finally, $\langle {A,B}\rangle =0$![]() if and only if $ab=cd=0$
if and only if $ab=cd=0$![]() .
.
Example 4.5 We study the concepts of orthogonality presented above for rank one operators, i.e., for operators of the form
where $x$![]() and $y$
and $y$![]() are given vectors in $\mathscr {H}$
are given vectors in $\mathscr {H}$![]() .
.
Let $x,y,u,v\in \mathscr {H}$![]() , and consider the operators $A=x\otimes y$
, and consider the operators $A=x\otimes y$![]() and $B=u\otimes v$
and $B=u\otimes v$![]() . Then $\|A\|=\|x\|\|y\|$
. Then $\|A\|=\|x\|\|y\|$![]() and $\|B\|=\|u\|\|v\|$
and $\|B\|=\|u\|\|v\|$![]() . In this case we have
. In this case we have

With the notation $a=\|u\|^{2}\|v\|^{2},\ b=\langle {u,x}\rangle \langle {y,v}\rangle ,\ c=\|x\|^{2}\|y\|^{2}$![]() and $d=\|x\|^{2}\|u\|^{2}|\langle {y,v}\rangle |^{2}+\|y\|^{2}\|v\|^{2}|\langle {u,x}\rangle |^{2}$
and $d=\|x\|^{2}\|u\|^{2}|\langle {y,v}\rangle |^{2}+\|y\|^{2}\|v\|^{2}|\langle {u,x}\rangle |^{2}$![]() , we observe that the Birkhoff–James orthogonality between $A$
, we observe that the Birkhoff–James orthogonality between $A$![]() and $B$
and $B$![]() takes the form:
takes the form:
Clearly, for $\lambda$![]() in a ‘small’ disk $D(0,\varepsilon )$
in a ‘small’ disk $D(0,\varepsilon )$![]() , $a|\lambda |^{2}+2\Re (\lambda b)\le c$
, $a|\lambda |^{2}+2\Re (\lambda b)\le c$![]() . Then, taking squares, formula (4) becomes:
. Then, taking squares, formula (4) becomes:
In particular, for $\mu ={\varepsilon }/{2}$![]() and, successively, $\lambda =\mu , \lambda =-\mu , \lambda =-i\mu$
and, successively, $\lambda =\mu , \lambda =-\mu , \lambda =-i\mu$![]() and $\lambda =i\mu$
and $\lambda =i\mu$![]() and by taking the limit when $\epsilon \to 0$
and by taking the limit when $\epsilon \to 0$![]() , one can deduce that $\Re b\ge 0, \Re b\le 0, \Im b\ge 0$
, one can deduce that $\Re b\ge 0, \Re b\le 0, \Im b\ge 0$![]() and, respectively, $\Im b\le 0$
and, respectively, $\Im b\le 0$![]() . This forces $b=0$
. This forces $b=0$![]() .
.
By symmetry, a similar condition holds true for the Birkhoff–James orthogonality between $B$![]() and $A$
and $A$![]() .
.
We can write the orthogonality, in the Roberts sense, between $A$![]() and $B$
and $B$![]() as:
as:
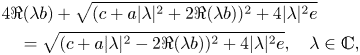
where $e=d-ac-|b|^{2}$![]() . By squaring the equation, we get:
. By squaring the equation, we get:
For $|\lambda |$![]() small enough, the quantity in the parenthesis becomes strictly positive (as $c$
small enough, the quantity in the parenthesis becomes strictly positive (as $c$![]() is strictly positive). Hence, $\Re (\lambda b)=0$
is strictly positive). Hence, $\Re (\lambda b)=0$![]() . So, by taking $\lambda \in \mathbb {R}_+$
. So, by taking $\lambda \in \mathbb {R}_+$![]() , respectively $\lambda \in i\mathbb {R}_+$
, respectively $\lambda \in i\mathbb {R}_+$![]() , we necessarily have $b=0$
, we necessarily have $b=0$![]() .
.
It is obvious that $b=0$![]() implies the orthogonalities $A\perp _BB, B\perp _BA$
implies the orthogonalities $A\perp _BB, B\perp _BA$![]() and $A\perp _RB$
and $A\perp _RB$![]() .
.
We showed that the following conditions are equivalent:
(i) $A\perp _B B$
 .
.(ii) $B\perp _B A$
 .
.(iii) $A\perp _R B$
 .
.(iv) $\langle {x,u}\rangle =0$
 or $\langle {y,v}\rangle =0$
or $\langle {y,v}\rangle =0$ .
.
Also, $A$![]() and $B$
and $B$![]() are orthogonal in the Pythagoras sense if and only if one of the following conditions holds true:
are orthogonal in the Pythagoras sense if and only if one of the following conditions holds true:
(a) $\{x,u\}$
 are linearly dependent and $\langle {y,v}\rangle =0.$
are linearly dependent and $\langle {y,v}\rangle =0.$
(b) $\{y,v\}$
 are linearly dependent and $\langle {x,u}\rangle =0$
are linearly dependent and $\langle {x,u}\rangle =0$ .
.
Indeed, after some computations for the case $b=0$![]() (Roberts and Birkhoff–James orthogonalities are necessary conditions), the orthogonality $A\perp _P B$
(Roberts and Birkhoff–James orthogonalities are necessary conditions), the orthogonality $A\perp _P B$![]() becomes:
becomes:
We obtain that $d=ac$![]() , which, in the case $\langle {y,v}\rangle =0$
, which, in the case $\langle {y,v}\rangle =0$![]() , leads us to the equality case in the Cauchy–Schwarz inequality, namely $|\langle {x,u}\rangle |=\|x\|\|u\|$
, leads us to the equality case in the Cauchy–Schwarz inequality, namely $|\langle {x,u}\rangle |=\|x\|\|u\|$![]() (i.e., $\{x,u\}$
(i.e., $\{x,u\}$![]() are linearly dependent). The situation when $\langle {x,u}\rangle =0$
are linearly dependent). The situation when $\langle {x,u}\rangle =0$![]() is treated similarly.
is treated similarly.
Moreover, one can easily see that the parallelogram law:
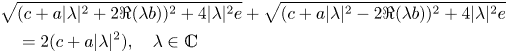
can be simplified as $e=0$![]() , which takes the form:
, which takes the form:
We deduce that $A$![]() and $B$
and $B$![]() satisfy the parallelogram law if and only if $\{x,u\}$
satisfy the parallelogram law if and only if $\{x,u\}$![]() or $\{y,v\}$
or $\{y,v\}$![]() are linearly dependent. Finally, $\langle {A,B}\rangle =0$
are linearly dependent. Finally, $\langle {A,B}\rangle =0$![]() if and only if $\langle {x,u}\rangle =0$
if and only if $\langle {x,u}\rangle =0$![]() .
.
Let $\mathcal {A}$![]() be a $C^{*}$
be a $C^{*}$![]() -algebra. For an element $a\in \mathcal {A}$
-algebra. For an element $a\in \mathcal {A}$![]() we denote by $m(a)$
we denote by $m(a)$![]() the minimum modulus of $|a|$
the minimum modulus of $|a|$![]() , i.e.,
, i.e.,
Evidently, for a positive element $a\in \mathcal {A}$![]() , $m(a)>0$
, $m(a)>0$![]() if and only if $a$
if and only if $a$![]() is invertible. The following theorem, which relates Birkhoff–James orthogonality with a weaker version of Pythagoras orthogonality, has been formulated in the context of Hilbert spaces by Barraa and Boumazgour in [Reference Barraa and Boumazgour5, Theorem 3] (see also [Reference Moslehian and Zamani16, Theorem 2.9]).
is invertible. The following theorem, which relates Birkhoff–James orthogonality with a weaker version of Pythagoras orthogonality, has been formulated in the context of Hilbert spaces by Barraa and Boumazgour in [Reference Barraa and Boumazgour5, Theorem 3] (see also [Reference Moslehian and Zamani16, Theorem 2.9]).
Theorem 4.6 Let $x$![]() and $y$
and $y$![]() be elements of a pre-Hilbert $\mathcal {A}$
be elements of a pre-Hilbert $\mathcal {A}$![]() -module. The following conditions are equivalent:
-module. The following conditions are equivalent:
(i) There exists $\varphi \in S_{|x|^{2}}(\mathcal {A})$
 such that $\varphi (\langle {x,y}\rangle )=0$
such that $\varphi (\langle {x,y}\rangle )=0$ .
.(ii) $x\perp _B y$
 .
.(iii) $\|x+\lambda y\|^{2}\ge \|x\|^{2}+|\lambda |^{2}m(|y|^{2}),\ \lambda \in \mathbb {C}$
 .
.
Proof. The equivalence $(i)\Leftrightarrow (ii)$![]() has been obtained by Arambašić and Rajić in [Reference Arambašić and Rajić3, Theorem 2.7] (see also [Reference Bhattacharyya and Grover8, Theorem 4.4]).
has been obtained by Arambašić and Rajić in [Reference Arambašić and Rajić3, Theorem 2.7] (see also [Reference Bhattacharyya and Grover8, Theorem 4.4]).
Clearly, $(ii)$![]() is a consequence of $(iii)$
is a consequence of $(iii)$![]() . Conversely, if $\varphi$
. Conversely, if $\varphi$![]() is a state of $\mathcal {A}$
is a state of $\mathcal {A}$![]() which verifies $\varphi (|x|^{2})=\|x\|^{2}$
which verifies $\varphi (|x|^{2})=\|x\|^{2}$![]() and $\varphi (\langle {x,y}\rangle )=0$
and $\varphi (\langle {x,y}\rangle )=0$![]() (by $(i)$
(by $(i)$![]() ), then, for every $\lambda \in \mathbb {C}$
), then, for every $\lambda \in \mathbb {C}$![]() ,
,

Condition $(iii)$![]() is proved.
is proved.
It was noted by James [Reference James12, Corollary 2.2] that, for any two elements $x$![]() and $y$
and $y$![]() of a normed linear space $\mathscr {X}$
of a normed linear space $\mathscr {X}$![]() there exists a number $\alpha$
there exists a number $\alpha$![]() such that $y\perp _B(x+\alpha y)$
such that $y\perp _B(x+\alpha y)$![]() . Such a condition is not valid, in full generality, for Pythagoras orthogonality. However, a weaker version might still be formulated. Its operator version can be found in [Reference Barraa and Boumazgour5, Corollary 4] (see also [Reference Moslehian and Zamani16, Corollary 2.11]).
. Such a condition is not valid, in full generality, for Pythagoras orthogonality. However, a weaker version might still be formulated. Its operator version can be found in [Reference Barraa and Boumazgour5, Corollary 4] (see also [Reference Moslehian and Zamani16, Corollary 2.11]).
Corollary 4.7 Let $x$![]() and $y$
and $y$![]() be elements of a pre-Hilbert module over $\mathcal {A}$
be elements of a pre-Hilbert module over $\mathcal {A}$![]() such that $m(|y|^{2})>0$
such that $m(|y|^{2})>0$![]() . Then there exists a unique $\alpha _0\in \mathbb {C}$
. Then there exists a unique $\alpha _0\in \mathbb {C}$![]() such that
such that
Moreover, one can find $\varphi \in S_{|x+\alpha y|^{2}}(\mathcal {A})$![]() such that $\varphi (\langle {x+\alpha y,y}\rangle )=0$
such that $\varphi (\langle {x+\alpha y,y}\rangle )=0$![]() if and only if $\alpha =\alpha _0$
if and only if $\alpha =\alpha _0$![]() .
.
Proof. We firstly observe that, since $\lim _{|\alpha |\to \infty }\|x+\alpha y\|=\infty$![]() ,
,
for a certain $\delta >0$![]() . In addition, as the map $\alpha \mapsto \|x+\alpha y\|$
. In addition, as the map $\alpha \mapsto \|x+\alpha y\|$![]() is continuous on the compact set $\{|\alpha |\le \delta \}$
is continuous on the compact set $\{|\alpha |\le \delta \}$![]() , it attains its minimum at some point $\alpha _0\in \mathbb {C}$
, it attains its minimum at some point $\alpha _0\in \mathbb {C}$![]() , that is, $\|x+\alpha _0y+\lambda y\|\ge \|x+\alpha _0y\|$
, that is, $\|x+\alpha _0y+\lambda y\|\ge \|x+\alpha _0y\|$![]() for every $\lambda \in \mathbb {C}$
for every $\lambda \in \mathbb {C}$![]() . Formula (5) then follows by Theorem 4.6 $(iii)$
. Formula (5) then follows by Theorem 4.6 $(iii)$![]() . If, for some $\alpha _1\in \mathbb {C}$
. If, for some $\alpha _1\in \mathbb {C}$![]() ,
,
then, by taking $\lambda =\alpha _0-\alpha _1$![]() , we obtain
, we obtain
so, $\alpha _1=\alpha _0$![]() . The final statement is a consequence, in view of the uniqueness of $\alpha _0$
. The final statement is a consequence, in view of the uniqueness of $\alpha _0$![]() , of Theorem 4.6 ($(i)\Leftrightarrow (iii$
, of Theorem 4.6 ($(i)\Leftrightarrow (iii$![]() )).
)).
As seen earlier, the Pythagoras orthogonality implies both the parallelogram law and Birkhoff–James orthogonality. In certain particular situations, the converse is also true.
Theorem 4.8 Let $\mathcal {A}$![]() be a unital $C^{*}$
be a unital $C^{*}$![]() -algebra with unit $e$
-algebra with unit $e$![]() . If $x$
. If $x$![]() and $y$
and $y$![]() are elements in a pre-Hilbert $\mathcal {A}$
are elements in a pre-Hilbert $\mathcal {A}$![]() -module such that $|y|^{2}=\alpha e$
-module such that $|y|^{2}=\alpha e$![]() ($\alpha >0$
($\alpha >0$![]() is given), then the following conditions are equivalent:
is given), then the following conditions are equivalent:
(i) $x$
 and $y$
and $y$ are orthogonal in the Pythagoras sense.
are orthogonal in the Pythagoras sense.(ii) $x$
 and $y$
and $y$ satisfy the parallelogram law and are Birkhoff–James orthogonal.
satisfy the parallelogram law and are Birkhoff–James orthogonal.
Proof. The direct implication is obvious. Conversely, if $(ii)$![]() holds true, then, by Theorem 4.6 $(iii)$
holds true, then, by Theorem 4.6 $(iii)$![]() ,
,
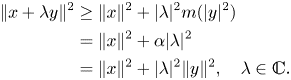
In view of the parallelogram law, the inequalities above become equalities. Hence $x\perp _P y$![]() , as required.
, as required.
The operator version of Theorem 4.6 ($(i)\Leftrightarrow (ii$![]() )) has been obtained by B. Magajna in [Reference Magajna15, Lemma 2.2] (see also [Reference Bhatia and Šemrl7, Remark 3.1]). It states that two bounded linear operators $A$
)) has been obtained by B. Magajna in [Reference Magajna15, Lemma 2.2] (see also [Reference Bhatia and Šemrl7, Remark 3.1]). It states that two bounded linear operators $A$![]() and $B$
and $B$![]() on $\mathscr {H}$
on $\mathscr {H}$![]() are orthogonal in the Birkhoff–James sense if and only if there exists a sequence $(\xi _n)_{n\ge 0}$
are orthogonal in the Birkhoff–James sense if and only if there exists a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() such that
such that
For Pythagoras orthogonality (a concept which is stronger than Birkhoff–James orthogonality), we must include certain additional conditions. One of the main tools in our developments is the following expression of the $\min _{\lambda \in \mathbb {C}}\|A+\lambda B\|$![]() .
.
Theorem 4.9 Arambašić and Rajić [Reference Arambašić and Rajić3, Proposition 2.1]
Let $A$![]() and $B$
and $B$![]() be bounded linear operators on $\mathscr {H}$
be bounded linear operators on $\mathscr {H}$![]() . Then
. Then
where
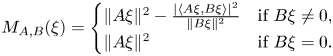
The following limit characterization provides a step forward in our desired description of Pythagoras orthogonality.
Lemma 4.10 Let $A$![]() and $B$
and $B$![]() be bounded linear operators acting on $\mathscr {H}$
be bounded linear operators acting on $\mathscr {H}$![]() such that
such that
for a certain $\lambda _0\in \mathbb {R}\setminus \{-1,0\}, \alpha \in \mathbb {C}\setminus \{0\}$![]() and $(\xi _n)_{n\ge 0}$
and $(\xi _n)_{n\ge 0}$![]() a sequence of unit vectors in $\mathscr {H}$
a sequence of unit vectors in $\mathscr {H}$![]() .
.
1 If $(A+\alpha B)\xi _n\ne 0,\ n\ge 0$
 and
(6)\begin{equation} M_{A,A+\alpha B}(\xi_n)\xrightarrow{n\to\infty}(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}, \end{equation}and $(x_n)$
and
(6)\begin{equation} M_{A,A+\alpha B}(\xi_n)\xrightarrow{n\to\infty}(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}, \end{equation}and $(x_n)$
 is a subsequence of $(\xi _n)$
is a subsequence of $(\xi _n)$ such that the limits
(7)\begin{equation} a=\lim_{n\to\infty}\|Ax_n\|,\ b=\lim_{n\to\infty}\|Bx_n\|\text{ and }c=\lim_{n\to\infty}\langle{Ax_n,Bx_n}\rangle \end{equation}exist, then $a, b,$
such that the limits
(7)\begin{equation} a=\lim_{n\to\infty}\|Ax_n\|,\ b=\lim_{n\to\infty}\|Bx_n\|\text{ and }c=\lim_{n\to\infty}\langle{Ax_n,Bx_n}\rangle \end{equation}exist, then $a, b,$
 and $c$
and $c$ satisfy the conditions
(8)\begin{equation} a^{2}(\lambda_0+1)+c\bar{\alpha}\lambda_0={-}b^{2}|\alpha|^{2}\lambda_0-c\bar{\alpha}(\lambda_0+1)=(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}. \end{equation}Moreover,
satisfy the conditions
(8)\begin{equation} a^{2}(\lambda_0+1)+c\bar{\alpha}\lambda_0={-}b^{2}|\alpha|^{2}\lambda_0-c\bar{\alpha}(\lambda_0+1)=(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}. \end{equation}Moreover, \[ \|(1+\lambda_0)A+\lambda_0\alpha B\|=\min_{\lambda\in\mathbb{C}}\|(1+\lambda)A+\lambda\alpha B\| \]and
\[ \|(1+\lambda_0)A+\lambda_0\alpha B\|=\min_{\lambda\in\mathbb{C}}\|(1+\lambda)A+\lambda\alpha B\| \]and (9)\begin{equation} \|A+\lambda B\|^{2}\ge\dfrac{\begin{matrix}[(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}][\lambda_0|\alpha|^{2}-(\lambda_0+1)|\lambda|^{2}]\\ -\bar{\alpha}c|\lambda_0\alpha-(\lambda_0+1)\lambda|^{2}\end{matrix}}{|\alpha|^{2}\lambda_0(\lambda_0+1)},\quad\lambda\in\mathbb{C}. \end{equation}
(9)\begin{equation} \|A+\lambda B\|^{2}\ge\dfrac{\begin{matrix}[(1+\lambda_0)^{2}\|A\|^{2}+\lambda_0^{2}|\alpha|^{2}\|B\|^{2}][\lambda_0|\alpha|^{2}-(\lambda_0+1)|\lambda|^{2}]\\ -\bar{\alpha}c|\lambda_0\alpha-(\lambda_0+1)\lambda|^{2}\end{matrix}}{|\alpha|^{2}\lambda_0(\lambda_0+1)},\quad\lambda\in\mathbb{C}. \end{equation}
2 Conversely, if the limits (7) exist, satisfy conditions (8) and $a^{2}\ne (1+\lambda _0)^{2}\|A\|^{2}+\lambda _0^{2}|\alpha |^{2}\|B\|^{2},$
 then (6) holds true.
then (6) holds true.
Proof. We may assume, without loss of generality, that $\alpha =1$![]() ($B$
($B$![]() can be replaced by $\left({1}/{\alpha}\right)B$
can be replaced by $\left({1}/{\alpha}\right)B$![]() , if necessary).
, if necessary).
Let us now observe that, for every $n\ge 0$![]() , the following inequalities hold true:
, the following inequalities hold true:
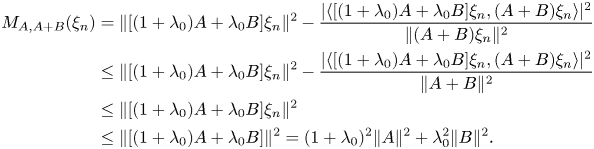
Letting $n\to \infty$![]() we conclude that (6) is equivalent with the following limit conditions:
we conclude that (6) is equivalent with the following limit conditions:
and
Following the notation of (7), one can write (11) as
Similarly, (12) takes the form
Easy computations then show that (11) and (12) are actually equivalent with (8).
According to these remarks, in order to prove $(a)$![]() , it only remains to let $n\to \infty$
, it only remains to let $n\to \infty$![]() into the formulas
into the formulas
and
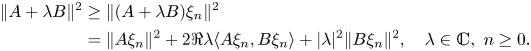
(b)![]() As seen above, (11) and (12) are a consequence of (8). In addition,
As seen above, (11) and (12) are a consequence of (8). In addition,
Hence, $\lim _{n\to \infty }\|(A+B)\xi _n\|>0$![]() , which shows that (10) also holds true. The proof is completed.
, which shows that (10) also holds true. The proof is completed.
Lemma 4.11 Let $A$![]() and $B$
and $B$![]() be bounded linear operators on $\mathscr {H}$
be bounded linear operators on $\mathscr {H}$![]() such that $\operatorname {rank}(A+\alpha _i B)=1$
such that $\operatorname {rank}(A+\alpha _i B)=1$![]() for pairwise distinct complex numbers $\alpha _i\in \mathbb {C}, i=1,2,3$
for pairwise distinct complex numbers $\alpha _i\in \mathbb {C}, i=1,2,3$![]() . Then $\operatorname {rank}(A+\alpha B)=1$
. Then $\operatorname {rank}(A+\alpha B)=1$![]() for every $\alpha \in \mathbb {C}$
for every $\alpha \in \mathbb {C}$![]() .
.
Proof. Let $x_1,x_2,y_1,y_2$![]() be non-null vectors in $\mathscr {H}$
be non-null vectors in $\mathscr {H}$![]() such that $A+\alpha _1 B=x_1\otimes y_1$
such that $A+\alpha _1 B=x_1\otimes y_1$![]() and $A+\alpha _2 B=x_2\otimes y_2$
and $A+\alpha _2 B=x_2\otimes y_2$![]() . Then
. Then
We distinguish two cases:
$(i)$![]() $\{x_1,x_2\}$
$\{x_1,x_2\}$![]() are linearly independent. Since $\operatorname {rank}(A+\alpha _3 B)=1$
are linearly independent. Since $\operatorname {rank}(A+\alpha _3 B)=1$![]() , one can find $\beta _1,\beta _2\in \mathbb {C}$
, one can find $\beta _1,\beta _2\in \mathbb {C}$![]() (at least one of them is non-null) such that $.$
(at least one of them is non-null) such that $.$![]() . Then, for every $z\in \mathscr {H}$
. Then, for every $z\in \mathscr {H}$![]() , there exists $\mu \in \mathbb {C}$
, there exists $\mu \in \mathbb {C}$![]() such that
such that
Therefore, $\beta _1,\beta _2$![]() are both non-null and ${\bar {\beta _2}(\bar {\alpha _3}-\bar {\alpha _2})}/{\bar {\alpha _1}-\bar {\alpha _2}}y_1-{\bar {\beta _1}(\bar {\alpha _1}-\bar {\alpha _3})}/{\bar {\alpha _1}-\bar {\alpha _2}}y_2=0$
are both non-null and ${\bar {\beta _2}(\bar {\alpha _3}-\bar {\alpha _2})}/{\bar {\alpha _1}-\bar {\alpha _2}}y_1-{\bar {\beta _1}(\bar {\alpha _1}-\bar {\alpha _3})}/{\bar {\alpha _1}-\bar {\alpha _2}}y_2=0$![]() , so $\{y_1,y_2\}$
, so $\{y_1,y_2\}$![]() are linearly dependent. In other words,
are linearly dependent. In other words,
$(ii)$![]() $\{x_1,x_2\}$
$\{x_1,x_2\}$![]() are linearly dependent. In this case, there exists a complex number $\beta \ne 0$
are linearly dependent. In this case, there exists a complex number $\beta \ne 0$![]() such that $x_2=\beta x_1$
such that $x_2=\beta x_1$![]() . We conclude that
. We conclude that
Since $\{A,B\}$![]() are linearly independent (as assumed earlier; this also implies that $\{y_1,y_2\}$
are linearly independent (as assumed earlier; this also implies that $\{y_1,y_2\}$![]() are linearly independent), we deduce that $A+\lambda B$
are linearly independent), we deduce that $A+\lambda B$![]() has rank one for every $\lambda \in \mathbb {C}$
has rank one for every $\lambda \in \mathbb {C}$![]() .
.
We are now ready to present the announced characterization of Pythagoras orthogonality.
Theorem 4.12 Let $A$![]() and $B$
and $B$![]() be bounded linear operators acting on $\mathscr {H}$
be bounded linear operators acting on $\mathscr {H}$![]() such that $\operatorname {rank}(A+\alpha _1 B)>1$
such that $\operatorname {rank}(A+\alpha _1 B)>1$![]() and $\Re (\alpha _2A^{*}B)\ge 0$
and $\Re (\alpha _2A^{*}B)\ge 0$![]() for certain $\alpha _1,\alpha _2\in \mathbb {C},\ \alpha _2\ne 0$
for certain $\alpha _1,\alpha _2\in \mathbb {C},\ \alpha _2\ne 0$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(i) $A$
 and $B$
and $B$ are orthogonal in the Pythagoras sense.
are orthogonal in the Pythagoras sense.(ii) $A$
 and $B$
and $B$ verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$
verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$ of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$ such that
\[ \|A\xi_n\|\xrightarrow{n\to\infty}\|A\|,\quad \|B\xi_n\|\xrightarrow{n\to\infty}\|B\|\text{ and }\langle{A\xi_n,B\xi_n}\rangle\xrightarrow{n\to\infty}0. \]
such that
\[ \|A\xi_n\|\xrightarrow{n\to\infty}\|A\|,\quad \|B\xi_n\|\xrightarrow{n\to\infty}\|B\|\text{ and }\langle{A\xi_n,B\xi_n}\rangle\xrightarrow{n\to\infty}0. \]
(iii) $A$
 and $B$
and $B$ verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$
verify the parallelogram law and there exists a sequence $(\xi _n)_{n\ge 0}$ of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$ such that
\[ \|(A+\lambda B)\xi_n\|^{2}\xrightarrow{n\to\infty}\|A\|^{2}+|\lambda|^{2}\|B\|^{2}\text{ for every }\lambda\in\mathbb{C}. \]
such that
\[ \|(A+\lambda B)\xi_n\|^{2}\xrightarrow{n\to\infty}\|A\|^{2}+|\lambda|^{2}\|B\|^{2}\text{ for every }\lambda\in\mathbb{C}. \]
Proof. $(i)\Rightarrow (ii)$![]() . The parallelogram law is obviously weaker than (or, at most equivalent to) Pythagoras orthogonality.
. The parallelogram law is obviously weaker than (or, at most equivalent to) Pythagoras orthogonality.
Our next aim is to prove the limit conditions of $(ii)$![]() . Since $\Re (2\alpha _2A^{*}B)\ge 0$
. Since $\Re (2\alpha _2A^{*}B)\ge 0$![]() and $\Re (3\alpha _2A^{*}B)\ge 0$
and $\Re (3\alpha _2A^{*}B)\ge 0$![]() and, by Lemma 4.11, at least one of the operators $A+\alpha _2 B$
and, by Lemma 4.11, at least one of the operators $A+\alpha _2 B$![]() , $A+2\alpha _2 B$
, $A+2\alpha _2 B$![]() and $A+3\alpha _2 B$
and $A+3\alpha _2 B$![]() has rank strictly greater than one, so we can assume that $\alpha _1=\alpha _2=\alpha$
has rank strictly greater than one, so we can assume that $\alpha _1=\alpha _2=\alpha$![]() . As we have previously done, we can also assume that $\alpha =1$
. As we have previously done, we can also assume that $\alpha =1$![]() . We firstly observe that, by $(i)$
. We firstly observe that, by $(i)$![]() ,
,
An easy computation then shows that
which is attained for $\lambda _0=-{\|A\|^{2}}/{\left(\|A\|^{2}+\|B\|^{2}\right)}$![]() . It follows from Theorem 4.9 and (14) that there exists a sequence $(\xi _n)_{n\ge 0}$
. It follows from Theorem 4.9 and (14) that there exists a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() such that
such that
We may suppose, eventually on a subsequence, that $(A+B)\xi _n\ne 0$![]() for every $n\ge 0$
for every $n\ge 0$![]() . Indeed, if, otherwise, $(A+B)\xi _n=0$
. Indeed, if, otherwise, $(A+B)\xi _n=0$![]() for every $n\ge n_0$
for every $n\ge n_0$![]() and for a certain $n_0\ge 0$
and for a certain $n_0\ge 0$![]() , then (15) takes the form
, then (15) takes the form
by the definition of $M_{A,A+B}$![]() . As $(A\xi _n)_{n\ge 0}$
. As $(A\xi _n)_{n\ge 0}$![]() is a bounded sequence in $\mathscr {H}$
is a bounded sequence in $\mathscr {H}$![]() , it contains a weakly convergent subsequence (denoted also by $(A\xi _n)_{n\ge 0}$
, it contains a weakly convergent subsequence (denoted also by $(A\xi _n)_{n\ge 0}$![]() ) to a vector $w\in \mathscr {H}$
) to a vector $w\in \mathscr {H}$![]() . Obviously, $\operatorname {span}\{(A+B)^{*}w\}\subsetneq \overline {\operatorname {ran}(A+B)^{*}}$
. Obviously, $\operatorname {span}\{(A+B)^{*}w\}\subsetneq \overline {\operatorname {ran}(A+B)^{*}}$![]() as the rank of $(A+B)^{*}$
as the rank of $(A+B)^{*}$![]() is strictly greater than $1$
is strictly greater than $1$![]() . Consequently, one can find a unit vector $e\in \overline {\operatorname {ran}(A+B)^{*}}$
. Consequently, one can find a unit vector $e\in \overline {\operatorname {ran}(A+B)^{*}}$![]() , which is orthogonal to $(A+B)^{*}w$
, which is orthogonal to $(A+B)^{*}w$![]() . Then, by setting $u_n=\sqrt {{n}/({n+1})}\xi _n+\left({1}/{\sqrt {n+1}}\right)e,\ n\ge 0$
. Then, by setting $u_n=\sqrt {{n}/({n+1})}\xi _n+\left({1}/{\sqrt {n+1}}\right)e,\ n\ge 0$![]() , we have
, we have
since $e\perp \ker (A+B)$![]() . Moreover, for $n\ge 0$
. Moreover, for $n\ge 0$![]() ,
,

In view of (16) and the observation that
we deduce, by passing to limit in (17), that
One may consider, in this particular situation, the sequence $(u_{n+n_0})_{n\ge 0}$![]() which will be also denoted by $(\xi _n)_{n\ge 0}$
which will be also denoted by $(\xi _n)_{n\ge 0}$![]() .
.
The assumptions of Lemma 4.10 $(a)$![]() are verified. So, the limits (7) satisfy the conditions (equivalent with (8))
are verified. So, the limits (7) satisfy the conditions (equivalent with (8))
We deduce that $c\le 0$![]() . Also, by hypothesis (i.e., $\Re (A^{*}B)\ge 0$
. Also, by hypothesis (i.e., $\Re (A^{*}B)\ge 0$![]() ),
),
This forces $c=0$![]() and, by (18), $a=\|A\|$
and, by (18), $a=\|A\|$![]() and $b=\|B\|$
and $b=\|B\|$![]() .
.
$(ii)\Rightarrow (iii)$![]() . Clearly, if a sequence $(\xi _n)_{n\ge 0}$
. Clearly, if a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() verifies $(ii)$
verifies $(ii)$![]() , then
, then
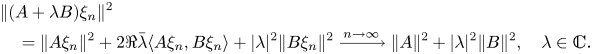
Hence $(\xi _n)_{n\ge 0}$![]() also verifies $(iii)$
also verifies $(iii)$![]() .
.
$(iii)\Rightarrow (i)$![]() . Let $(\xi _n)_{n\ge 0}$
. Let $(\xi _n)_{n\ge 0}$![]() be a sequence of unit vectors in $\mathscr {H}$
be a sequence of unit vectors in $\mathscr {H}$![]() such that $(iii)$
such that $(iii)$![]() holds true. Then
holds true. Then
The proof is finished, as before, by the use of the parallelogram law.
Remark 4.13 $(a)$![]() The necessity of the rank condition. Let $A$
The necessity of the rank condition. Let $A$![]() and $B$
and $B$![]() be bounded linear operators on $\mathscr {H}$
be bounded linear operators on $\mathscr {H}$![]() such that, for every $\alpha \in \mathbb {C}$
such that, for every $\alpha \in \mathbb {C}$![]() , $A+\alpha B$
, $A+\alpha B$![]() is a rank one operator. Then, as seen in the proof of Lemma 4.11, one of the following two situations can occur:
is a rank one operator. Then, as seen in the proof of Lemma 4.11, one of the following two situations can occur:
$(i)$![]() $(A,B)=(x\otimes y_A,x\otimes y_B)$
$(A,B)=(x\otimes y_A,x\otimes y_B)$![]() , with $x,y_A,y_B\in \mathscr {H}$
, with $x,y_A,y_B\in \mathscr {H}$![]() , $x\ne 0$
, $x\ne 0$![]() and $\{y_A,y_B\}$
and $\{y_A,y_B\}$![]() linearly independent. Then, by Example 4.5, $(A,B)$
linearly independent. Then, by Example 4.5, $(A,B)$![]() satisfies the parallelogram law. Moreover, $A\perp _P B$
satisfies the parallelogram law. Moreover, $A\perp _P B$![]() if and only if $\langle {y_A,y_B}\rangle =0$
if and only if $\langle {y_A,y_B}\rangle =0$![]() . Condition $(ii)$
. Condition $(ii)$![]() of Theorem 4.12 takes, for a given sequence $(\xi _n)_{n\ge 0}$
of Theorem 4.12 takes, for a given sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() , the form:
, the form:
This is, however, impossible.
$(ii)$![]() $(A,B)=(x_A\otimes y,x_B\otimes y)$
$(A,B)=(x_A\otimes y,x_B\otimes y)$![]() , with $x_A,x_B,y\in \mathscr {H}$
, with $x_A,x_B,y\in \mathscr {H}$![]() , $\{x_A,x_B\}$
, $\{x_A,x_B\}$![]() linearly independent and $y\ne 0$
linearly independent and $y\ne 0$![]() . Again by Example 4.5, $(A,B)$
. Again by Example 4.5, $(A,B)$![]() satisfies the parallelogram law. We also observe that a sequence $(\xi _n)_{n\ge 0}$
satisfies the parallelogram law. We also observe that a sequence $(\xi _n)_{n\ge 0}$![]() of unit vectors in $\mathscr {H}$
of unit vectors in $\mathscr {H}$![]() with $|\langle {\xi _n,y}\rangle |\xrightarrow {n\to \infty }\|y\|$
with $|\langle {\xi _n,y}\rangle |\xrightarrow {n\to \infty }\|y\|$![]() satisfies condition $(ii)$
satisfies condition $(ii)$![]() of Theorem 4.12 if and only if $\langle {x_A,x_B}\rangle =0$
of Theorem 4.12 if and only if $\langle {x_A,x_B}\rangle =0$![]() or, equivalently, $A\perp _P B$
or, equivalently, $A\perp _P B$![]() . On the other hand, $A\perp _P B$
. On the other hand, $A\perp _P B$![]() if and only if $A^{*}\perp _P B^{*}$
if and only if $A^{*}\perp _P B^{*}$![]() , but condition $(ii)$
, but condition $(ii)$![]() of Theorem 4.12 is not verified for the pair $(A^{*},B^{*})$
of Theorem 4.12 is not verified for the pair $(A^{*},B^{*})$![]() (as seen in case $(i)$
(as seen in case $(i)$![]() above).
above).
$(b)$![]() The necessity of the parallelogram law. Let us consider, as in Example 4.4, $A=M_I(1,0,0,1)$
The necessity of the parallelogram law. Let us consider, as in Example 4.4, $A=M_I(1,0,0,1)$![]() , $B=M_I(0,1,1,0)$
, $B=M_I(0,1,1,0)$![]() and $h\in \mathscr {H}$
and $h\in \mathscr {H}$![]() a vector of unit norm. Then $A$
a vector of unit norm. Then $A$![]() and $B$
and $B$![]() do not satisfy the parallelogram law while, for $\xi =(h,0)$
do not satisfy the parallelogram law while, for $\xi =(h,0)$![]() , $\|A\xi \|=\|A\|=1,\ \|B\xi \|=\|B\|=1$
, $\|A\xi \|=\|A\|=1,\ \|B\xi \|=\|B\|=1$![]() and $\langle {A\xi ,B\xi }\rangle =\langle {(h,0),(0,h)}\rangle =0$
and $\langle {A\xi ,B\xi }\rangle =\langle {(h,0),(0,h)}\rangle =0$![]() .
.
$(c)$![]() The importance of the condition $\Re (\alpha A^{*}B)\ge 0$
The importance of the condition $\Re (\alpha A^{*}B)\ge 0$![]() for certain nonzero $\alpha \in \mathbb {C}$
for certain nonzero $\alpha \in \mathbb {C}$![]() . Let $x$
. Let $x$![]() and $y$
and $y$![]() be unit vectors in $\mathscr {H}$
be unit vectors in $\mathscr {H}$![]() such that $\langle {x,y}\rangle =0$
such that $\langle {x,y}\rangle =0$![]() (it is assumed that $\dim \mathscr {H}\ge 2$
(it is assumed that $\dim \mathscr {H}\ge 2$![]() ). If $S=x\otimes x+y\otimes y$
). If $S=x\otimes x+y\otimes y$![]() and $T=x\otimes y$
and $T=x\otimes y$![]() , then the operators $A=\left (\begin {smallmatrix} S & 0\\0 & 0\end {smallmatrix}\right )$
, then the operators $A=\left (\begin {smallmatrix} S & 0\\0 & 0\end {smallmatrix}\right )$![]() and $B=\left (\begin {smallmatrix} 0 & T\\0 & 0\end {smallmatrix}\right )$
and $B=\left (\begin {smallmatrix} 0 & T\\0 & 0\end {smallmatrix}\right )$![]() are orthogonal in the Pythagoras sense (according to Example 4.3) and $\operatorname {rank}(A+\alpha B)=2$
are orthogonal in the Pythagoras sense (according to Example 4.3) and $\operatorname {rank}(A+\alpha B)=2$![]() for every $\alpha \in \mathbb {C}$
for every $\alpha \in \mathbb {C}$![]() . Moreover, for $h_1,h_2\in \mathscr {H}$
. Moreover, for $h_1,h_2\in \mathscr {H}$![]() and $\alpha \in \mathbb {C},\ \alpha \ne 0$
and $\alpha \in \mathbb {C},\ \alpha \ne 0$![]() , it holds
, it holds
Hence,
Also, condition $(ii)$![]() of Theorem 4.12 can be expressed by the existence of sequences $(\xi _n)_{n\ge 0}$
of Theorem 4.12 can be expressed by the existence of sequences $(\xi _n)_{n\ge 0}$![]() and $(\eta _n)_{n\ge 0}$
and $(\eta _n)_{n\ge 0}$![]() of vectors in $\mathscr {H}$
of vectors in $\mathscr {H}$![]() with $\|\xi _n\|^{2}+\|\eta _n\|^{2}=1,\ n\ge 0$
with $\|\xi _n\|^{2}+\|\eta _n\|^{2}=1,\ n\ge 0$![]() such that
such that
Equivalently,
Letting $n\to \infty$![]() in the Cauchy–Schwarz inequalities $|\langle {\xi _n,y}\rangle |\le \|\xi _n\|$
in the Cauchy–Schwarz inequalities $|\langle {\xi _n,y}\rangle |\le \|\xi _n\|$![]() and $|\langle {\eta _n,y}\rangle |\le \|\eta _n\|$
and $|\langle {\eta _n,y}\rangle |\le \|\eta _n\|$![]() ($n\ge 0$
($n\ge 0$![]() ), we deduce that the limits $\lim _{n\to \infty }\|\xi _n\|$
), we deduce that the limits $\lim _{n\to \infty }\|\xi _n\|$![]() and $\lim _{n\to \infty }\|\eta _n\|$
and $\lim _{n\to \infty }\|\eta _n\|$![]() exist and they are both equal to $1$
exist and they are both equal to $1$![]() . This contradicts, however, the equality $\|\xi _n\|^{2}+\|\eta _n\|^{2}=1,\ n\ge 0$
. This contradicts, however, the equality $\|\xi _n\|^{2}+\|\eta _n\|^{2}=1,\ n\ge 0$![]() .
.