We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the minimum spanning tree problem on a weighted complete bipartite graph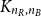 
$K_{n_R, n_B}$ whose 
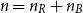$n=n_R+n_B$ vertices are random, i.i.d. uniformly distributed points in the unit cube in 
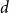$d$ dimensions and edge weights are the 
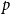$p$-th power of their Euclidean distance, with 
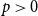$p\gt 0$. In the large 
$n$ limit with 
$n_R/n \to \alpha _R$ and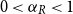 
$0\lt \alpha _R\lt 1$, we show that the maximum vertex degree of the tree grows logarithmically, in contrast with the classical, non-bipartite, case, where a uniform bound holds depending on 
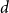$d$ only. Despite this difference, for 
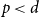$p\lt d$, we are able to prove that the total edge costs normalized by the rate 
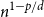$n^{1-p/d}$ converge to a limiting constant that can be represented as a series of integrals, thus extending a classical result of Avram and Bertsimas to the bipartite case and confirming a conjecture of Riva, Caracciolo and Malatesta.
