The well-known Erdős-Hajnal conjecture states that for any graph 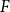 $F$, there exists
$F$, there exists 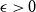 $\epsilon \gt 0$ such that every
$\epsilon \gt 0$ such that every  $n$-vertex graph
$n$-vertex graph 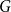 $G$ that contains no induced copy of
$G$ that contains no induced copy of 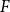 $F$ has a homogeneous set of size at least
$F$ has a homogeneous set of size at least 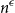 $n^{\epsilon }$. We consider a variant of the Erdős-Hajnal problem for hypergraphs where we forbid a family of hypergraphs described by their orders and sizes. For graphs, we observe that if we forbid induced subgraphs on
$n^{\epsilon }$. We consider a variant of the Erdős-Hajnal problem for hypergraphs where we forbid a family of hypergraphs described by their orders and sizes. For graphs, we observe that if we forbid induced subgraphs on 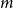 $m$ vertices and
$m$ vertices and 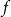 $f$ edges for any positive
$f$ edges for any positive 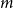 $m$ and
$m$ and 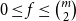 $0\leq f \leq \binom{m}{2}$, then we obtain large homogeneous sets. For triple systems, in the first nontrivial case
$0\leq f \leq \binom{m}{2}$, then we obtain large homogeneous sets. For triple systems, in the first nontrivial case 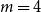 $m=4$, for every
$m=4$, for every 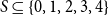 $S \subseteq \{0,1,2,3,4\}$, we give bounds on the minimum size of a homogeneous set in a triple system where the number of edges spanned by every four vertices is not in
$S \subseteq \{0,1,2,3,4\}$, we give bounds on the minimum size of a homogeneous set in a triple system where the number of edges spanned by every four vertices is not in 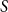 $S$. In most cases the bounds are essentially tight. We also determine, for all
$S$. In most cases the bounds are essentially tight. We also determine, for all 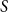 $S$, whether the growth rate is polynomial or polylogarithmic. Some open problems remain.
$S$, whether the growth rate is polynomial or polylogarithmic. Some open problems remain.