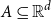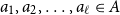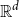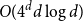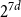1 results
On convex holes in d-dimensional point sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 101-108
-
- Article
- Export citation
-
Given a finite set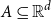
$A \subseteq \mathbb{R}^d$, points 
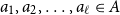$a_1,a_2,\dotsc,a_{\ell} \in A$ form an 
$\ell$-hole in A if they are the vertices of a convex polytope, which contains no points of A in its interior. We construct arbitrarily large point sets in general position in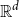 
$\mathbb{R}^d$ having no holes of size 
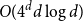$O(4^dd\log d)$ or more. This improves the previously known upper bound of order 
$d^{d+o(d)}$ due to Valtr. The basic version of our construction uses a certain type of equidistributed point sets, originating from numerical analysis, known as (t,m,s)-nets or (t,s)-sequences, yielding a bound of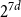 
$2^{7d}$. The better bound is obtained using a variant of (t,m,s)-nets, obeying a relaxed equidistribution condition.
