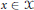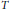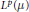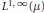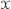Let $T_{1}$, $T_{2}$ be two Calderón–Zygmund operators and $T_{1,b}$ be the commutator of $T_{1}$ with symbol $b\in \text{BMO}(\mathbb{R}^{n})$. In this paper, by establishing new bilinear sparse dominations and a new weighted estimate for bilinear sparse operators, we prove that the composite operator $T_{1}T_{2}$ satisfies the following estimate: for $\unicode[STIX]{x1D706}>0$ and weight $w\in A_{1}(\mathbb{R}^{n})$,

$$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log \bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx,\nonumber\end{eqnarray}$$

$T_{1,b}T_{2}$

$$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1,b}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}^{2}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log ^{2}\bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx.\nonumber\end{eqnarray}$$

Let $\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu \right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that $\mu \left( \left\{ x \right\} \right)\,=\,0$ for all 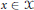$x\,\in \,\text{ }\!\!\chi\!\!\text{ }$. 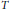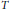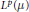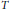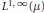In this paper, we show that the boundedness of a Calderón–Zygmund operator $T$ on ${{L}^{2}}\left( \mu \right)$ is equivalent to that of $T$ on ${{L}^{p}}\left( \mu \right)$ for some $p\,\in \,\left( 1,\,\infty \right)$, and that of $T$ from ${{L}^{1}}\left( \mu \right)$ to ${{L}^{1,\,\infty }}\left( \mu \right)$. As an application, we prove that if 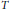$T$ is a Calderón–Zygmund operator bounded on ${{L}^{2}}\left( \mu \right)$, then its maximal operator is bounded on 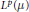${{L}^{p}}\left( \mu \right)$ for all $p\,\in \,\left( 1,\,\infty \right)$ and from the space of all complex-valued Borel measures on 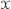$\text{ }\!\!\chi\!\!\text{ }$ to 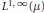${{L}^{1,\,\infty }}\left( \mu \right)$. All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.

We investigate Laplace type and Laplace–Stieltjes type multipliers in the d-dimensional setting of the Dunkl harmonic oscillator with the associated group of reflections isomorphic to ℤd2 and in the related context of Laguerre function expansions of convolution type. We use Calderón–Zygmund theory to prove that these multiplier operators are bounded on weighted Lp, 1<p<∞, and from L1 to weak L1.

Let $\mu$ be a positive Radon measure on $\mathbb{R}^d$ which satisfies $\mu(B(x,r))\le Cr^{n}$ for any $x\in\mathbb{R}^d$ and $r>0$ and some fixed constants $C>0$ and $n\in(0,d]$. In this paper, a new characterization of the space $\rbmo(\mu)$, which was introduced by Tolsa, is given. As an application, it is proved that the $L^p(\mu)$-boundedness with $p\in(1,\infty)$ of Calderón–Zygmund operators is equivalent to various endpoint estimates.