We prove some results concerning convolutions, additive energies, and sumsets of convex sets and their generalizations. In particular, we show that if a set 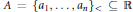 $A\,=\,{{\{{{a}_{1}},\,.\,.\,.\,,\,{{a}_{n}}\}}_{<}}\,\subseteq \,\mathbb{R}$ has the property that for every fixed
$A\,=\,{{\{{{a}_{1}},\,.\,.\,.\,,\,{{a}_{n}}\}}_{<}}\,\subseteq \,\mathbb{R}$ has the property that for every fixed 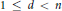 $1\,\le \,d\,<\,n$, all differences
$1\,\le \,d\,<\,n$, all differences 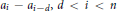 ${{a}_{i}}\,-\,{{a}_{i-d}},\,d\,<\,i\,<n$, are distinct, then
${{a}_{i}}\,-\,{{a}_{i-d}},\,d\,<\,i\,<n$, are distinct, then  $\left| A\,+\,A \right|\,\gg \,{{\left| A \right|}^{3/2+c}}$ for a constant
$\left| A\,+\,A \right|\,\gg \,{{\left| A \right|}^{3/2+c}}$ for a constant 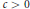 $c\,>\,0$.
$c\,>\,0$.