Let  $A$ be a subgroup of a finite group
$A$ be a subgroup of a finite group 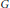 $G$ and
$G$ and 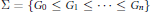 $\sum \,=\,\{{{G}_{0}}\,\le \,{{G}_{1}}\,\le \,.\,.\,.\,\le \,{{G}_{n}}\}$ some subgroup series of
$\sum \,=\,\{{{G}_{0}}\,\le \,{{G}_{1}}\,\le \,.\,.\,.\,\le \,{{G}_{n}}\}$ some subgroup series of 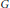 $G$. Suppose that for each pair
$G$. Suppose that for each pair 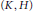 $\left( K,\,H \right)$ such that
$\left( K,\,H \right)$ such that 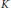 $K$ is a maximal subgroup of
$K$ is a maximal subgroup of 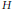 $H$ and
$H$ and 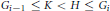 ${{G}_{i-1}}\,\le \,K\,<\,H\,\le \,{{G}_{i}}$, for some i, either
${{G}_{i-1}}\,\le \,K\,<\,H\,\le \,{{G}_{i}}$, for some i, either 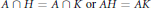 $A\,\cap \,H\,=\,A\,\cap \,K\,\text{or}\,\text{AH}\,\text{=}\,\text{AK}$. Then
$A\,\cap \,H\,=\,A\,\cap \,K\,\text{or}\,\text{AH}\,\text{=}\,\text{AK}$. Then  $A$ is said to be
$A$ is said to be  $\sum$-embedded in
$\sum$-embedded in 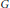 $G$. And
$G$. And  $A$ is said to be
$A$ is said to be 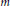 $m$-embedded in
$m$-embedded in 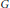 $G$ if
$G$ if 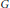 $G$ has a subnormal subgroup
$G$ has a subnormal subgroup 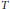 $T$ and
$T$ and 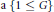 $a\,\{1\,\le \,G\}$-embedded subgroup
$a\,\{1\,\le \,G\}$-embedded subgroup  $C$ in
$C$ in 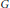 $G$ such that
$G$ such that 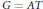 $G\,=\,AT$ and
$G\,=\,AT$ and  $T\cap A\,\le \,C\,\le \,A$. In this article, some sufficient conditions for a finite group
$T\cap A\,\le \,C\,\le \,A$. In this article, some sufficient conditions for a finite group 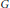 $G$ to be
$G$ to be  $p$-nilpotent are given whenever all subgroups with order
$p$-nilpotent are given whenever all subgroups with order 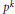 ${{p}^{k}}$ of a Sylow
${{p}^{k}}$ of a Sylow  $p$-subgroup of
$p$-subgroup of 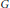 $G$ are
$G$ are  $m$-embedded for a given positive integer
$m$-embedded for a given positive integer  $k$.
$k$.