This paper is the first of a two part series devoted to describing relations between congruence and crystallographic braid groups. We recall and introduce some elements belonging to congruence braid groups and we establish some (iso)-morphisms between crystallographic braid groups and corresponding quotients of congruence braid groups.

Given a group $G$ and an integer $n\geq 0$, we consider the family ${\mathcal F}_n$ of all virtually abelian subgroups of $G$ of $\textrm{rank}$ at most $n$. In this article, we prove that for each $n\ge 2$ the Bredon cohomology, with respect to the family ${\mathcal F}_n$, of a free abelian group with $\textrm{rank}$ $k \gt n$ is nontrivial in dimension 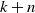$k+n$; this answers a question of Corob Cook et al. (Homology Homotopy Appl. 19(2) (2017), 83–87, Question 2.7). As an application, we compute the minimal dimension of a classifying space for the family ${\mathcal F}_n$ for braid groups, right-angled Artin groups, and graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups, for all 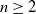$n\ge 2$. The main tools that we use are the Mayer–Vietoris sequence for Bredon cohomology, Bass–Serre theory, and the Lück–Weiermann construction.

Using totally symmetric sets, Chudnovsky–Kordek–Li–Partin gave a superexponential lower bound on the cardinality of non-abelian finite quotients of the braid group. In this paper, we develop new techniques using multiple totally symmetric sets to count elements in non-abelian finite quotients of the braid group. Using these techniques, we improve the lower bound found by Chudnovsky et al. We exhibit totally symmetric sets in the virtual and welded braid groups and use our new techniques to find superexponential bounds for the finite quotients of the virtual and welded braid groups.

We introduce the idea of a geometric categorical Lie algebra action on derived categories of coherent sheaves. The main result is that such an action induces an action of the braid group associated to the Lie algebra. The same proof shows that strong categorical actions in the sense of Khovanov–Lauda and Rouquier also lead to braid group actions. As an example, we construct an action of Artin’s braid group on derived categories of coherent sheaves on cotangent bundles to partial flag varieties.

We show that the restriction of the Dehornoy ordering to an appropriate free subgroup of the three-strand braid group defines a left-ordering of the free group on k generators, k>1, that has no convex subgroups.

Let $\mathbbm{k}$ be a (topological) field of characteristic 0. To any representation of a given Hopf algebra $\mathfrak{B}_n(\mathbbm{k})$, one can associate (using a Drinfeld associator) a representation $\widehat{\Phi}(\rho)$ of the braid group over the field $\mathbbm{k}((h))$ of Laurent series. We investigate the dependence on $\Phi$ of $\widehat{\Phi}(\rho)$ for a certain class of representations (so-called GT-rigid representations) and from this dependence deduce (continuous) projective representations of the Grothendieck–Teichmüller group $GT_1(\mathbbm{k})$; in particular, for $\mathbbm{k} = \mathbbm{Q}_l$ we obtain representations of the absolute Galois group of $\mathbbm{Q}(\mu_{l^{\infty}})$. In most situations, these projective representations can be decomposed into linear characters, as we do for the representations of the Iwahori–Hecke algebra of type A. In this case, moreover, we express $\widehat{\Phi}(\rho)$ when $\Phi$ is even and obtain unitary matrix models for the representations of the Iwahori–Hecke algebra. The representations of this algebra corresponding to hook diagrams have noteworthy properties under the action of $GT_1(\mathbbm{k})$.